非牛顿流体中在线双气泡相互作用的数值模拟
李少白,徐双,范俊赓,黄思源
(沈阳航空航天大学 能源与环境学院,沈阳 110136)
能源与环境工程
非牛顿流体中在线双气泡相互作用的数值模拟
李少白,徐双,范俊赓,黄思源
(沈阳航空航天大学 能源与环境学院,沈阳 110136)
利用Fluent软件采用SIMPLE算法,数值模拟了非牛顿流体中在线双气泡之间的相互作用。先行气泡和跟随气泡之间的相互作用与两气泡之间的中心间距有关,无因次距离S*越小,先行气泡和跟随气泡聚并融合为一个气泡的时间越短,当无因次距离S*增大到一定程度时,两气泡之间不会发生聚并,最终会以各自不同的速度上升。随着气泡之间的无因次距离S*增大,先行气泡与跟随气泡速度之比不断减小,直至先行气泡和跟随气泡速度之比为1,跟随气泡不受先行气泡的尾流影响。液相的流变性质不同,先行气泡和跟随气泡速度之比为1时的无因次距离S*也不同,非牛顿性越强,先行气泡尾流部分的剪切变稀作用越强,先行气泡对跟随气泡的影响的距离越大,先行气泡与跟随气泡速度之比减小的越快。
非牛顿流体;气泡;相互作用;数值模拟
非牛顿流体中的气泡运动广泛存在于能源、环境、化工等工业过程中,如沼气液、污泥或高分子溶液等都是典型的非牛顿流体[1],因此不管是理论基础研究还是工程实际应用,研究非牛顿流体中的气泡运动行为都具有较高的学术价值[2-3]。在这些过程中,气泡之间的相互作用会影响其周围的液相湍动状况、气液两相的界面面积,进而影响到相间的传热、传质速度[4-6]。为此,近年来许多学者针对非牛顿流体中的相互作用展开了研究。Kee D等人[7]利用高速摄像技术对非牛顿流体中的气泡形状及聚并行为进行了观察,考察了流变性质、表面张力对气泡性状及聚并的影响。Sousa等人[8]利用PIV技术对Taylor气泡在非牛顿流体中的相互作用时的流场信息进行了观察,认为非牛顿流体中的气泡相互作用距离大于牛顿流体。Fan等人[9]则利用PIV观察了非牛顿流体中平行上升双气泡的流场特性。事实上,非牛顿流体中相互作用的气泡之间有平行、在线及呈一定角度等多种方式,其中双气泡的在线相互作用是最简单,也是最基础的一种方式。因此,本文通过数值模拟方法对非牛顿流体中垂直在线的相互作用进行了研究,探讨了气泡间的距离和流体流变性质对气泡相互作用的影响。
1 计算模型
1.1 控制方程
气泡在非牛顿流体中的运动所涉及到的控制方程主要有连续性方程、动量方程,本过程为常温常压过程,液相可看做不可压缩流体,其连续性方程为
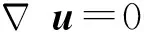
(1)
其中,u表示速度矢量。
不可压缩流体的动量方程如式(2)所示。
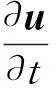
(2)
式中,ρ表示密度,F为质量力,μ表示流体的粘度,p表示流体内应力。
混合流体的密度和黏度计算方法如式(3)、式(4)所示。
ρ(F)=ρl(F)+ρg(1-F)
(3)
μ(F)=μl(F)+μg(1-F)
(4)
对于非牛顿流体而言,其粘度随着剪切速率的变化而变化,可用幂律模型表示为
(5)

(6)
采用VOF方法追踪气液界面,采用该方法时,计算域内的流体的含量通过体积分数函数表示。其中F=0表示计算域内为纯气相,F=1表示纯液相,0 (7) 追踪界面通过求解体积分率函数的对流方程来实现,如式(8)所示。 (8) 其中,对于气液两相的体积分率而言,应满足归一化,如式(9)所示。 Fl+Fg=1 (9) 最后,本文采用SIMPLE算法进行双气泡相互作用过程的求解。 几何模型如图1所示,选取的模型的边界尺寸为50 mm×150 mm,由于气泡直径一般选择2~10 mm,所以在该矩形区域内可以忽略壁面影响。上边界为出口,边界条件设为压力出口,其他 图1 二维计算模型示意图 几个壁面为光滑无滑动壁面。根据网格的独立性,选取边长为0.2 mm、0.3 mm、0.4 mm三种网格系统。三种网格尺寸下,单气泡上升速度如图2所示,从图中可以看出,网格尺寸对单气泡上升速度没有什么影响,考虑到网格数越多,计算时间越长,对计算机的要求也越高;又考虑到计算结果的精确性,所以选择网格边长为0.3 mm的网格系统。 图2 网格对气泡上升速度的影响 非牛顿流体中的气泡运动主要受到流体的流变性质、气泡尺寸以及气泡的排列方式等因素的影响。本文主要模拟了三种不同流变性质的流体,其物理性质如表1所示。 表1 模拟流体的物理及流变性质 未验证非牛顿流体中气泡运动模拟结果的可靠性,最具说服力的方法就是将模拟结果与实验结果相对比。但是,对于具体实验而言,气泡在线相互作用的数据获得十分困难,为此,本研究将对模拟过程中稳定上升后的单气泡运动的实验结果与数值模拟结果进行对比,并说明数值模拟的可靠性。图3为非牛顿流体单气泡模拟结果与实验结果的对比,从图中可以看出,总体上模拟结果和实验结果吻合良好。国内外许多研究表明[10-11],与牛顿流体相比,在适当的条件下,非牛顿流体中气泡会出现尖端的尾部,由图3可以看出,本研究的模拟也出现了该现象。 气泡的不同排列方式对气泡之间相互作用的影响各不相同,当两个气泡在同一条直线上时,先行气泡的运动会对跟随气泡上升速度和运动状态有一定的影响。在研究气泡之间的间距与气泡上升速度之间的关系时,为了方便研究,气泡之间距离无因次变量S*,其定义为 S*=L/D (10) 其中,L为气泡中心间距,D为气泡直径。 图3 实验所得的单气泡的形状与模拟结果的对比 在线气泡上升过程如图4所示,从中可以看出,两个体积相同的气泡在线上升运动过程,先行气泡和跟随气泡一起上升,在上升的过程中两气泡逐渐变形,先行气泡的形状在水平方向上拉伸,跟随气泡则在竖直方向上拉伸。图4给出气泡体积相同,但气泡之间初始间距不相同的三种情况下气泡相互作用模拟结果,从图中可以看出无因次距离S*越小,先行气泡和跟随气泡聚并融合为一个气泡的时间越短,两气泡聚并为一个气泡后,新的气泡体积是原来气泡体积的两倍,速度相对于在同等条件下单气泡要略大。当无因次距离S*增大到一定程度时,两气泡之间不会发生聚并,最终以各自最终速度上升。先行气泡在上升过程,其尾部会产生一个尾流区域,在该区域非牛顿流体剪切变稀,在先行气泡尾流的作用下,跟随气泡上升过程中加速度比先行气泡要大,经过一段时间后,当跟随气泡最终追赶上先行气泡,与先行气泡发生相互作用,最终两气泡聚并为一个气泡。模拟所得的非牛顿流体中的相互作用与文献中报道的非牛顿流体中气泡相互作用过程十分相符[12-13],表明了模拟结果的准确性和可靠性。 在线气泡上升过程,上升速度随时间变化如图5所示,图中给出三种不同浓度聚丙烯酰胺-PAA溶液单气泡与双气泡速度之间的关系。从图中可以看出,气泡体积相同的情况下,在线双气泡的速度比单独条件下的单气泡速度大。双气泡在线运动过程中,跟随气泡的速度要大于先行气泡,这是由于先行气泡在运动过程中,其气泡尾部有一个“尾流”区域[14]。在这个先行气泡的“尾流”区域内,由于非牛顿流体的剪切变稀的性质,跟随气泡在进入“尾流”区域进行加速运动,所以跟随气泡的速度要大于先行气泡的速度。此外,先行气泡尾流部分的流场速度要大于周围流体的流速。溶液浓度越低,“尾流”区域内流体的粘度越小,因此流体1中先行气泡与跟随气泡速度要大于流体2和流体3的气泡运动速度。 图4 在线双气泡上升过程模拟结果图 图5 气泡上升速度随时间变化关系 先行气泡和跟随气泡是否发生聚并对气液两相流之间的相互作用很重要。初始距离是影响气泡是否发生聚并的一个很重要的因素,为了研究在线气泡运动过程中两气泡的临界间距对聚并的影响,在模拟过程中选取了距离的无因次变量S*=2、3、4、5、6、7、8、9、10。图6给出了流体流变性质及两气泡速度比与无因次距离S*之间的关系,从图中可以看出,随着气泡之间的间距S*增大,先行气泡和跟随气泡的速度之比接近1,这是由于两气泡之间的间距越小,跟随气泡越容易受到先行气泡的影响,当两气泡之间的间距增大到一定程度,跟随气泡不受先行气泡尾流的影响。从图6中还可以看出,液相的流变性质不同,先行气泡和跟随气泡速度之比为1时气泡的间距S*也不同,流体1中双气泡的临界S*约为4.5左右,流体2中的临界S*约为5左右,流体3中的临界S*约为5.5左右。这是由于非牛顿性越强,先行气泡尾流部分的剪切变稀作用越强,先行气泡对跟随气泡的影响的距离越大。先行气泡与跟随气泡速度之比减小的越快,这与Li[15]等人的实验结果类似。 图6 气泡间距与两气泡速度之比的关系 采用数值模拟手段对非牛顿流体中在线双气泡之间的相互作用进行了研究,主要得到如下主要结论。 (1)先行气泡和跟随气泡之间的相互作用与两气泡之间的中心间距有关,无因次距离S*越小,先行气泡和跟随气泡聚并融合为一个气泡的时间越短,当无因次距离S*增大到一定程度时,两气泡之间不会发生聚并,最终会以各自不同的速度上升。 (2)随着气泡之间的无因次距离S*增大,先行气泡与跟随气泡速度之比不断减小,直至先行气泡和跟随气泡速度之比为1时,跟随气泡不受先行气泡的尾流影响。 (3)液相的流变性质不同,先行气泡和跟随气泡速度之比为1时的无因次距离S*也不同,非牛顿性越强,先行气泡尾流部分的剪切变稀作用越强,先行气泡对跟随气泡的影响的距离越大。先行气泡与跟随气泡速度之比减小得越快。 [1] CHHABRA R P.Bubbles,Drops and Particles in Non-Newtonian Fluids[M].2nded CRC Press:Boca Raton,FL,2007. [2] FAN W,SUN Y,CHEN H.Bubble Volume and Aspect Ratio Generated in Non‐Newtonian Fluids[J].Chemical Engineering & Technology,2015,37(9):1566-1574. [3] 李少白,徐双,范俊赓,等.粘弹性流体中气泡上升过程的轨迹[J].沈阳航空航天大学学报,2016,33(5):88-92. [4] ABOULHASANZADEH B,TRYGGVASON G.Effect of bubble interactions on mass transfer in bubbly flow[J].International Journal of Heat & Mass Transfer,2014,79:390-396. [5] GRACE S P S J R.Effect of Bubble Interaction on Interphase Mass Transfer in Gas Fluidized Beds[J].Chemical Engineering Science,1981,36(2):327-335. [6] ABOULHASANXADEH B,TRYGGVASON G.Effect of bubble-bubble interaction on mass transfer in bubbly flow using a multi-scale approach[C].65th Annual Meeting of the APS Division of Fluid Dynamics.American Physical Society,San Diego,2012. [7] KEE D D,CHHABRA R P.A photographic study of shapes of bubbles and coalescence in non-Newtonian polymer solutions[J].Rheologica Acta,1988,27(6):656-660. [8] SOUSA R G,PINTO A M F R,CAMPOS J B L M.Interaction between Taylor bubbles rising in stagnant non-Newtonian fluids[J].International Journal of Multiphase Flow,2007,33(9):970-986. [9] FAN W,YOUGUANG M A,XIAOLEI L I,et al.Study on the Flow Field around Two Parallel Moving Bubbles and Interaction Between Bubbles Rising in CMC Solutions by PIV[J].Chinese Journal of Chemical Engineering,2009,17(6):904-913. [10]LIU Y J,LIAO T Y,JOSEPH D D.A two-dimensional cusp at the trailing edge of an air bubble rising in a viscoelastic liquid[J].Journal of Fluid Mechanics,1995,304(304):321-342. [11]BELMONTE A.Self-oscillations of a cusped bubble rising through a micellar solution[J].Rheologica Acta,2000,39(6):554-559. [12]LIN T J,LIN G M.The Mechanisms of bubble coalescence in a non-Newtonian fluid[J].Canadian Journal of Chemical Engineering,2003,81(3-4):476-482. [13]LIN T J,LIN G M.Mechanisms of in-line coalescence of two-unequal bubbles in a non-Newtonian fluid[J].Chemical Engineering Journal,2009,155(3):750-756. [14]SOUSA R G,RIETHMULLER M L,PINTO A M F R,et al.Flow around individual Taylor bubbles rising in stagnant polyacrylamide (PAA) solutions[J].Journal of Non-Newtonian Fluid Mechanics,2006,135(1):16-31. [15]LI H Z,MOULINE Y,FUNFSCHILLING D,et al.Evidence for in-line bubble interactions in non-Newtonian fluids[J].Chemical Engineering Science,1998,53(12):2219-2230. (责任编辑:刘划 英文审校:赵欢) Numericalsimulationofinteractionbetweenin-linetwobubblesinnon-Newtonianfluids LI Shao-bai,XU Shuang,FAN Jun-geng,HUANG Si-yuan (College of Energy and Environment,Shenyang Aerospace University,Shenyang 110136,China) Interaction between in-line two bubbles in non-Newtonian fluids was studied numerically by Fluent software and SIMPLE algorithm.The results showed that the interaction between leading bubble and following bubble was related to center distance between the two bubbles.The smaller the dimensionless distanceS*,the shorter the time that the two bubbles coalesce each other.However,the coalescence will not occur when theS*increased and exceeded a certain value.Finally the two bubbles rose separately with different speed.Moreover,the velocity ratio between the two bubbles decreased with the increase ofS*,and then following bubble was independent on the leading bubble as the ratio approached to 1.The rheological property of liquid phase impacted theS*value when the ratio was equal to 1.The bigger the rheological property of liquid phase,the stronger the shear action of stern for the leading bubble and the effects of the leading bubbles on the following bubbles,which in turn resulted in the smaller velocity ratio. non-Newtonian fluids;bubble;interaction;numerical simulation 2017-06-15 国家自然科学基金(项目编号:21406141) 李少白(1982-),男,辽宁朝阳人,博士,主要研究方向:复杂的气液两相体系的传递特性,E-mail: lishaobai1982@163.com。 2095-1248(2017)04-0063-06 TQ021.1 : A 10.3969/j.issn.2095-1248.2017.04.008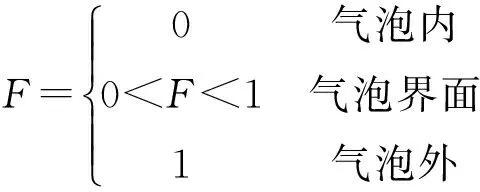
1.2 几何模型及网格划分
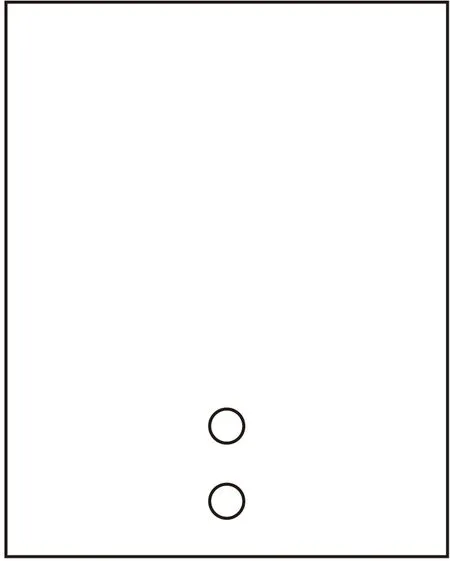
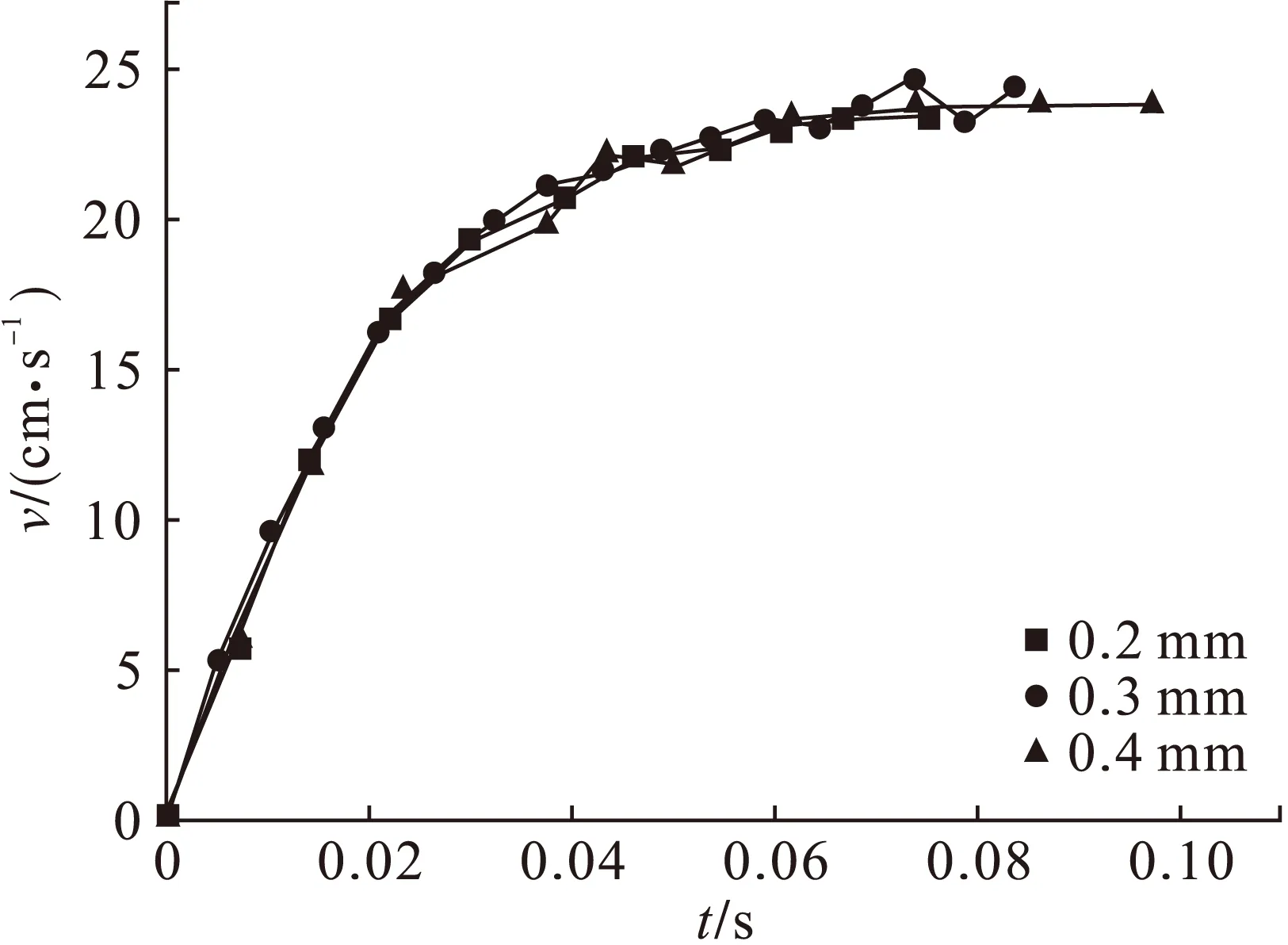
2 结果与分析
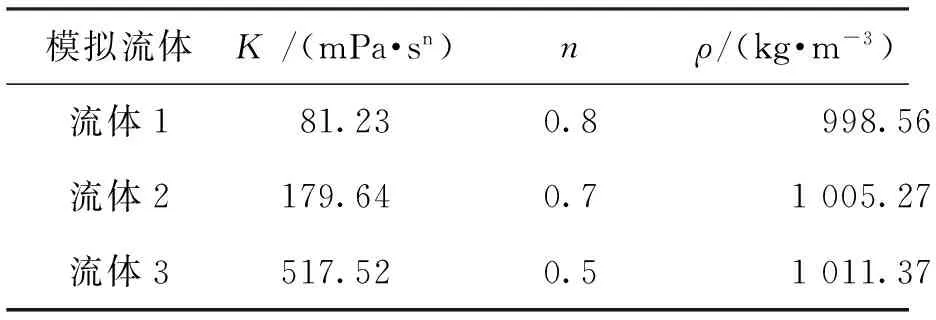



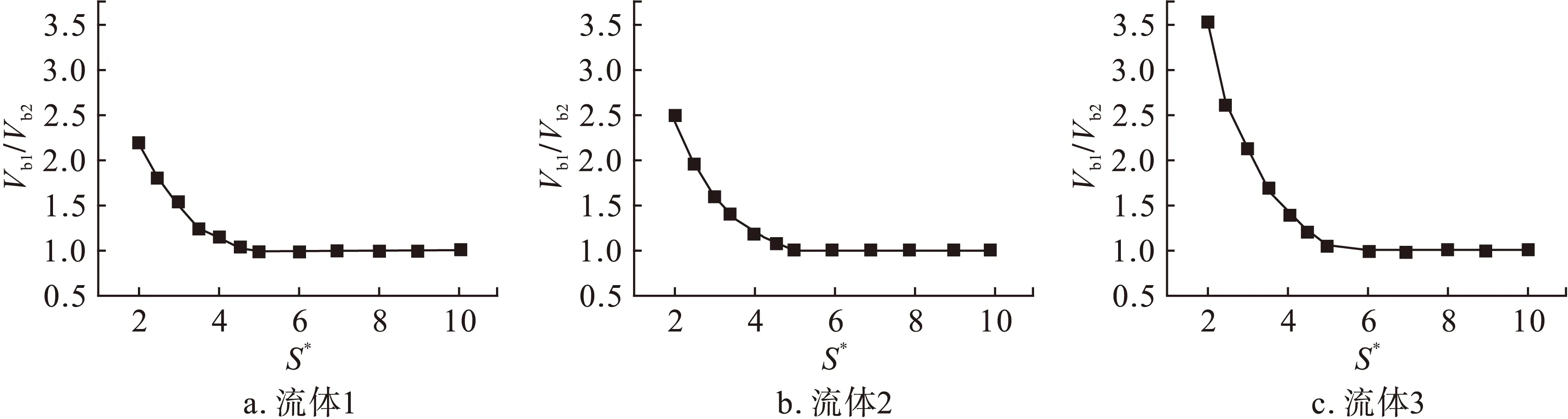
3 结论

