考虑尺度依赖的平面正交各向异性功能梯度Mindlin板静弯曲模型

贺 丹，杨子豪

(沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室,沈阳 110136)

考虑尺度依赖的平面正交各向异性功能梯度Mindlin板静弯曲模型

贺 丹，杨子豪

(沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室,沈阳 110136)

基于各向异性修正偶应力理论建立了能够考虑尺度依赖的平面正交各向异性功能梯度板静弯曲模型。模型中引入两个正交材料尺度参数，因此能够分别描述正交方向上不同程度的尺度效应。基于虚功原理推导了平衡方程和边界条件，并以受双向正弦载荷作用的简支板为例分析了尺度效应对板弯曲挠度产生的影响。算例结果表明：基于模型得到的板弯曲挠度总是小于传统一阶剪切板理论给出的结果，即捕捉到了尺度效应；尺度效应在尺度参数与几何尺寸接近时显著，而在几何尺寸远大于尺度参数时消失；此外，功能梯度变化指数和板跨厚比也会对尺度效应产生一定影响。

修正偶应力理论；功能梯度材料；正交各向异性；尺度效应；材料尺度参数

功能梯度材料是由两种或两种以上组份材料混合制备的先进复合材料。与传统复合材料层合结构相比，功能梯度材料因其具有沿梯度方向连续变化的力学性能有效避免了传统层合结构中由层间应力不连续导致的结构脱层失效，从而被广泛应用到实际工程领域，其中就包括微米/纳米量级的装置和系统，如：薄膜[1-2]、原子力显微镜[3]、微机电系统(MEMS)[4]、纳机电系统(NEMS)[5]以及生物传感装置[6]。

当材料进入到微尺度领域，其力学性能往往表现出较宏观状态更高的刚度，这种现象被称为材料力学行为的尺度效应[7-8]。传统的连续介质理论由于缺乏描述微观结构特性的方法而无法对尺度效应做出合理的解释。非传统广义连续介质理论，如：应变梯度理论[9]和偶应力理论[10-11]则通过引入材料尺度参数(MLSPs)而具备了这种能够描述尺度效应的能力。其中，偶应力理论可以被视为应变梯度理论的一种特殊形式，但包含更少的MLSP。由于这些参数都只能通过复杂的试验来进行测定，因此包含更少尺度参数的理论在工程应用的便利上更具优势。

Yang等[12]在传统偶应力理论的基础上提出了一种只含有一个MLSP的修正偶应力理论，该理论被广泛应用到微尺度功能梯度梁/板力学性能的分析中[13-15]。值得注意的是，修正偶应力理论是一种各向同性理论，而少数学者[16-17]通过该理论建模各向异性结构则意味着在保留材料宏观各向异性的同时忽略了微观各向异性。为了能够建立微尺度下层合板/梁结构的力学模型,陈万吉[18]提出了一种适用于各向异性材料的新修正偶应力理论，并基于该理论开展了一系列对微尺度层合梁/板弯曲[19]、振动[20]、稳定[21]等问题的研究。在该理论中，分别表征纤维和基体的两个MLSPs被引入到本构方程中并最终忽略了基体MLSP，而这种忽略较小尺度参数的做法显然不适用于各方向上微观结构差异较小的正交各向异性功能梯度材料。

本文首次尝试在一阶剪切板理论的基础上，将正交各向异性功能梯度板拓展至微观尺度，建立能够描述尺度效应的平面正交各向异性功能梯度板静弯曲模型。模型中引入两个沿正交方向用于描绘微观结构特性的材料尺度参数,使其在考虑材料宏观各向异性的同时也把微观各向异性考虑在内，由此具备了分别描述由尺度效应带来的两个正交方向上不同程度的板弯曲刚度增强的能力。

1 新修正偶应力理论

由陈万吉[18]提出的新修正偶应力理论将各向同性修正偶应力理论[12]推广至各向异性领域。在该理论中，应变张量的定义与传统理论相同，曲率张量则被重新定义为

χij=ωi,j

(1)

其中：ui为平动位移；ωi=eijkuk,j/2为转动位移；由式(1)可以清楚地看到应变张量εij是对称的，而曲率张量χij是非对称的。本构关系定义为

σij=Cijklεkl

(2)

式(2)中：σij和mij是对称的应力张量与偶应力张量；Cijkl为刚度矩阵系数；Gi(i=1,2,3)为各向异性材料不同方向上的剪切模量；i(i=1,2)则为两个正交方向上用于描绘材料微观结构特性的MLSPs(修正偶应力理论中其数量唯一)。

2 考虑尺度依赖的平面正交各向异性功能梯度板

由两种功能梯度组份材料构成的平面正交各向异性功能梯度矩形板的几何尺寸，坐标系的建立如图1所示。其中：a为板的长度，b为宽度，h为板的总厚度。

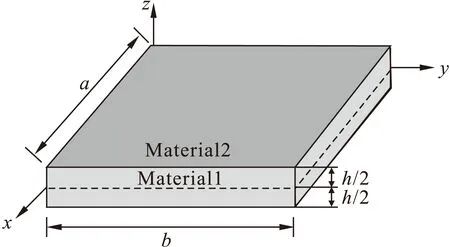
图1 平面正交各向异性功能梯度板的几何尺寸和坐标系

2.1 几何方程

本文模型采用一阶剪切变形Mindlin板理论，即将板的位移表示为

u(x,y,z)=u0(x,y)+zθx(x,y)

v(x,y,z)=v0(x,y)+zθy(x,y)

w(x,y)=w(x,y)

(3)

其中：u，v，w分别为板任意一点沿x轴，y轴和z轴方向上的位移；u0，v0为板几何形心面上一点沿x轴和y轴方向上的位移；θx和θy分别为绕x轴和y轴的截面转角。将式(3)代入到式(1)中，得到板的应变分量

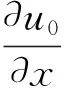
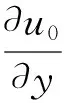
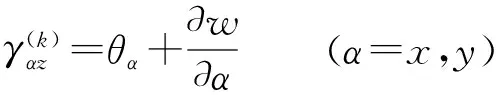
(4)

板的转动位移可由表达式θi=eijkuk,j/2及式(3)得到

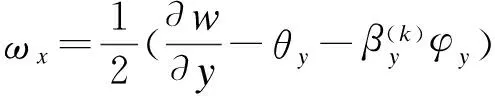
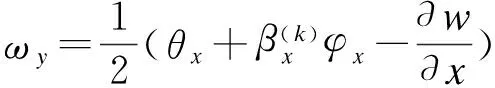
(5)

其中：ωz=0假定[22]被用来简化公式和减少计算量而不会造成任何误差。将式(3)代入到式(1)中可以得到板的非零曲率分量

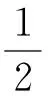
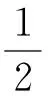
(6)

2.2 本构关系

对于如图1所示的正交各向异性功能梯度微板，假设其宏观材料属性(如：弹性模量、剪切模量)沿厚度方向遵循式(7)中的幂指数形式[23]连续变化

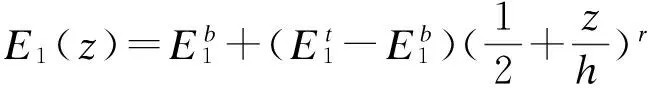
(7)

其中：r为功能梯度变化指数；h为梁的高度，z为梁内一点距梁几何形心面的距离；角标t、b分别代表功能梯度梁的顶端和底部；E1、E2、G12、G13、G23分别为正交各向异性材料不同方向上的弹性模量和剪切模量。

由式(2)可知：各向异性修正偶应力理论下的正交各向异性弹性体本构关系可以表示为

σ=Cε

(8)

其中：

σ=[σx,σy,τxy,τxz,τyz,mx,my,mxy,myx]T，

ε=[εx,εy,γxy,γxz,γyz,χx,χy,χxy,χyx]T,C为忽略横法向应力的刚度矩阵。

(9)

其中：Ci(z)(i=11,12,21,22,44,55,66)为宏观状态下与应力-应变有关的弹性矩阵系数；1(z)，2(z)则为两个正交方向上与微观状态下偶应力-曲率有关的MLSPs。对于功能梯度板来说，这些系数均为沿板厚度方向坐标z的函数，而这些系数与工程弹性常数之间的关系，可在相关文献[24]中获得。

3 基于虚功原理的平衡方程和边界条件

通过虚功原理来推导平面正交各向异性功能梯度微板的平衡方程和边界条件。该原理可以表述为

δU-δW=0

(10)

其中：基于新修正偶应力理论的虚应变能δU可以表示为

δU=∭V(σxδεx+σyδεy+τxyδγxy+τxzδγxz+

τyzδγyz+mxδχx+myδχy+mxyδχxy+myxδχyx)dV

(11)

式(11)中：V为整个板区域。虚外力功δW为

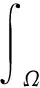
(12)

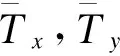
(13)

将式(11)和(12)代入式(10)中得到用内力表示的平衡方程及边界条件

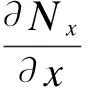
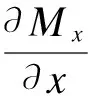
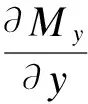
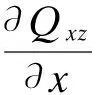
+q=0

(14)

式(14)中与传统合力、合力距以及偶应力力矩相关的符号定义为：

(NxMxNyMyNxyMxyQxzQyzYxYyYxyYyx)=

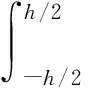
其中：Ks为横向剪切修正系数。边界条件为

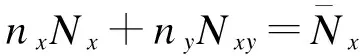
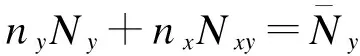
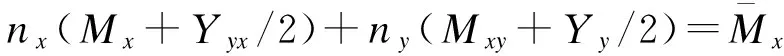
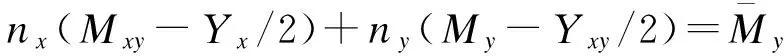
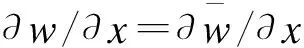
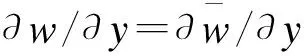
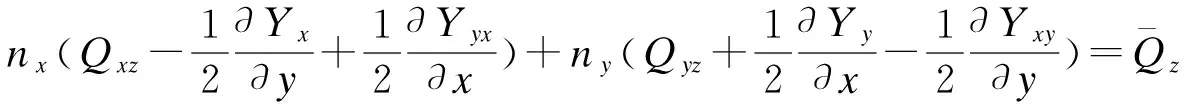
(15)

式(15)中：nx，ny为板边界外法线方向余弦。

4 算例分析

采用如图2所示的受双向正弦载荷作用的功能梯度简支板。其中，板的宏观材料属性在沿板厚度方向遵循式(7)中的幂指数形式连续变化。同时，假设板的微观属性(MLSPs)及泊松比沿板厚度方向保持不变。双向正弦载荷q=q0sin(πx/a)sin(πy/b)。

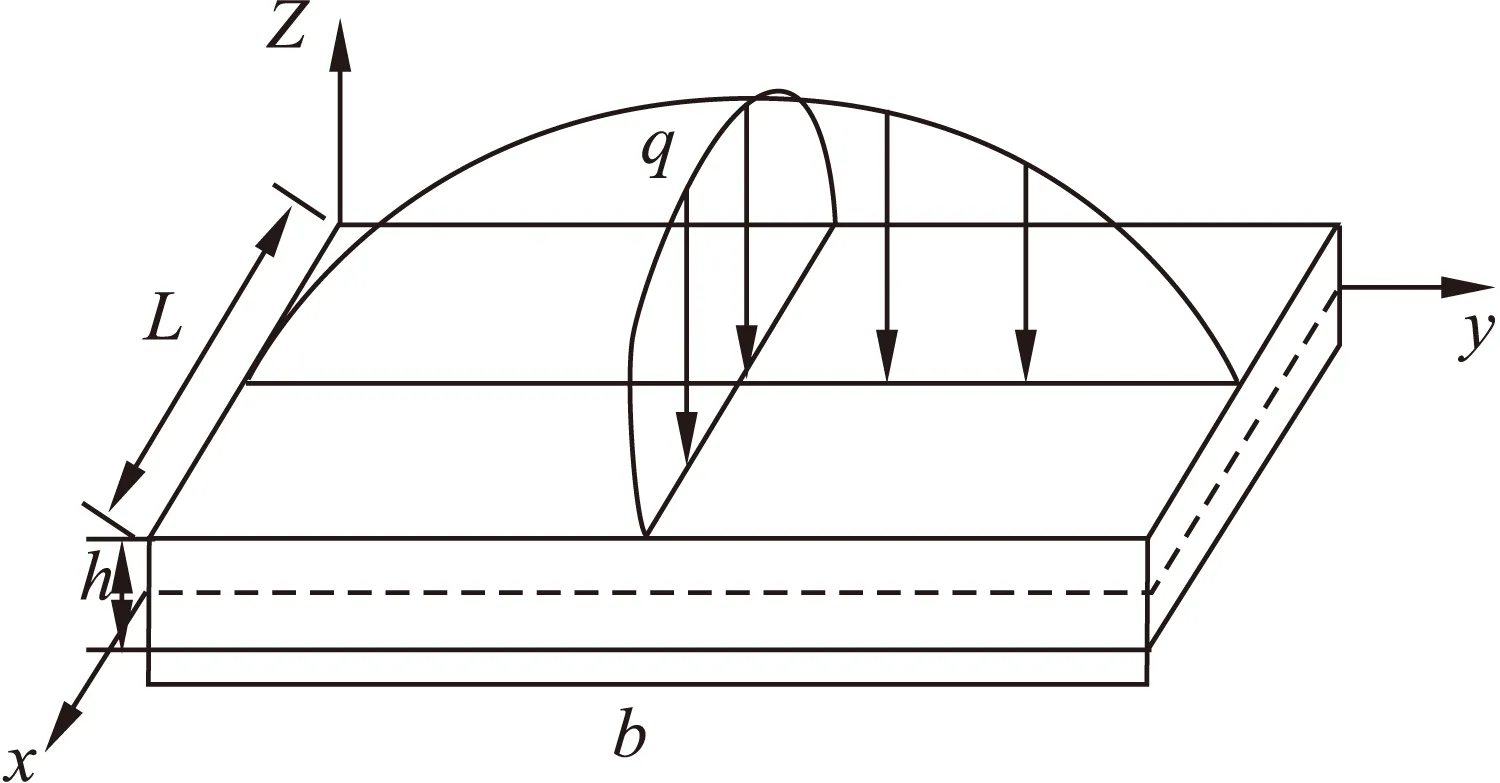
图2 受双向正弦载荷作用的功能梯度简支板

简支板的边界条件为

x=0,a:v0=w=∂w/∂y=θy=φy=Nx=Mx=Yyx=0

y=0,b:u0=w=∂w/∂x=θx=φx=Ny=My=Yxy=0

(16)

满足所有边界条件的位移试函数将取为

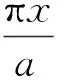
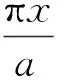
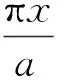
(17)

将式(17)代入到平衡方程(14)中，便可以得到位移试函数中的未知系数{U,V,W,Θx,Θy}，从而获得完整板位移表达式。简支板的工程弹性常数以及横向剪切修正系数如表1所示。

表1 微尺度平面正交各向异性功能梯度梁的弹性模量及工程常数

4.1 功能梯度微板中的尺度效应

本节主要研究多组跨厚比下功能梯度方板中的尺度效应对板弯曲挠度产生的影响。其中，与参考文献[25]一致的无量纲处理为

(18)

当板跨厚比取不同值时，尺度效应对功能梯度微板弯曲挠度产生的影响如图3所示。图3中，横坐标分别为两个正交方向上的MLSPs与板厚度h的比值；纵坐标为无量纲挠度。功能梯度变化指数r在本算例中取值为3。

由图3可知：当功能梯度微板的几何形状保持不变(a/2h=constant)时，基于本文模型所预测的无量纲挠度总是小于基于传统一阶剪切变形板理论得到的结果。此时，简支板表现出较宏观状态下更高的抗弯刚度，结构出现所谓的“尺度效应”；尺度效应会在MLSPs与板几何尺寸接近时更加明显，而在几何尺寸远大于MLSPs时消失。这种趋势与微弯曲试验中观察到的现象一致，因此可以证明本文模型能够有效地捕捉和反映尺度效应，而这是传统板理论无法做到的。此外，由尺度效应引起的板弯曲刚度增强在两个正交方向上程度不一。这种由微观各向异性导致的现象最终被引入两个MLSPs的本文模型解释，弥补了以往各向同性偶应力理论模型的不足。

4.2 板跨厚比对尺度效应产生的影响

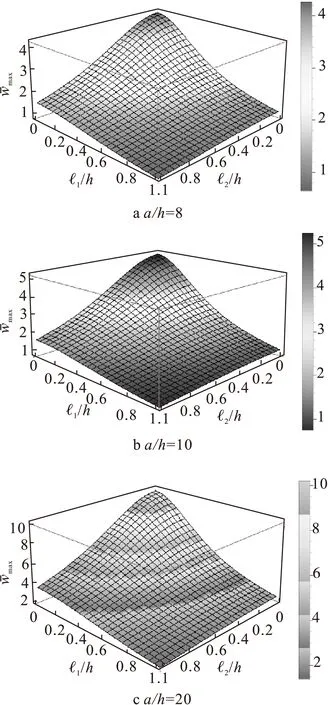
图3 MLSPs取不同值时功能梯度微板的全局响应

由图4可知：基于本文模型得到的在板y=b/2处的弯曲挠度均小于基于传统一阶剪切板理论得到的结果；当MLSPs一定时，二者间的差值随着功能梯度微板跨厚比的增加而逐渐变大。由此可以推断：当板跨厚比较小，模型较厚时，尺度效应消失。

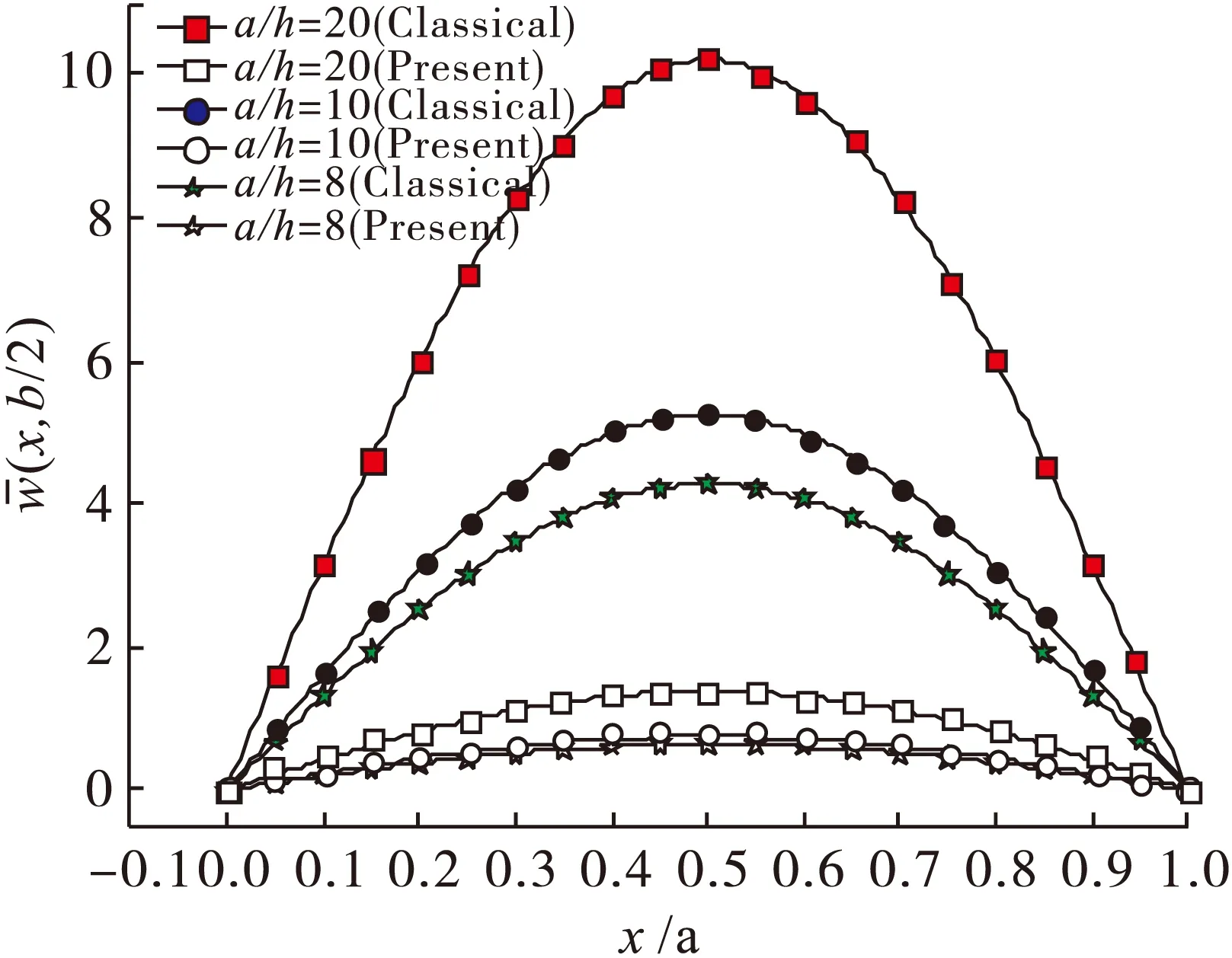
图4 不同板理论下，功能梯度微板在y=b/2处弯曲挠度对比图

4.3 功能梯度变化指数对尺度效应产生的影响

当微板MLSPs及几何形状保持不变时，功能梯度变化指数r对尺度效应的影响如图5所示。图5中，横坐标为功能梯度变化指数；纵坐标为基于本文模型(p)得到的简支板无量纲挠度与传统一阶剪切变形理论(c)结果的比值，其值越小，尺度效应越明显。

由图5可知：当简支板几何形状和MLSPs保持不变时，不同板理论下简支板无量纲挠度的比值随着功能梯度变化指数的增加先是明显减小。在达到最小值后，随着r值的继续增大，比值缓慢增加，简支板表现出的尺度效应逐渐减弱，但并不会消失，而是逐渐收敛于某一特定值。同时，通过对比图5中板跨厚比取不同值的3条曲线可以发现，随着板跨厚比的减小，尺度效应逐渐减弱，验证了算例4.2中得到的结论。

5 结论

(1)本文在各向异性修正偶应力理论的基础上建立了能够描述尺度效应的功能梯度微板静弯曲模型。模型中引入了两个沿着正交方向上的材料尺度参数，因此能够分别描述两个正交方向上由尺度效应带来的不同程度的板弯曲刚度增强。

(2) 基于本文模型得到的简支板无量纲挠度总是小于传统一阶剪切变形板理论给出的结果。此时微板表现出较宏观状态下更高的抗弯刚度，即捕捉到尺度效应。

(3) 当板跨厚比保持不变时，尺度效应在MLSPs与板几何尺寸接近时显著，而在几何尺寸远大于MLSPs时消失；当MLSPs保持不变，尺度效应随板跨厚比的增加而逐渐增强。当板跨厚比较小，模型较厚时，尺度效应消失。

(4) 功能梯度变化指数对尺度效应也有一定的影响，这种影响与功能梯度材料具体的变化形式有关，其相关结论可以为今后关于功能梯度夹心微梁/板的研究分析提供参考。

[1] FU Y,DU H,HUANG W,et al.TiNi-based thin films in MEMS applications:a review[J].Sensors & Actuators A Physical，2004,112(2-3):395-408.

[2] FU Y,DU H,ZHANG S.Functionally graded TiN/TiNi shape memory alloy films[J].Materials Letters,2003,57(20):2995-2999.

[3] RAHAEIFARD M,KAHROBAIYAN M H,AHMADIAN M T.Sensitivity analysis of atomic force microscope cantilever made of functionally graded materials[Z].San Diego.USA:American Society of Mechanical Engineers,2009539-544.

[4] WITVROUW A,MEHTA A.The use of functionally graded poly-SiGe layers for MEMS applications[C].Trans Tech Publ,2005.

[5] LEE Z,OPHUS C,FISCHER L M,et al.Metallic NEMS components fabricated from nanocomposite Al-Mo films[J].Nanotechnology,2006,17(12):3063-3070.

[6] SHAAT M,ABDELKEFI A.Modeling of mechanical resonators used for nanocrystalline materials characterization and disease diagnosis of HIVs[J].Springer-Verlag,2016,22(2):305-318.

[7] FLECK N A,MULLER G M,ASHBY M F,et al.Strain gradient plasticity:Theory and experiment[J].Acta Metallurgica Et Materialia,1994,42(2):475-487.

[8] STÖLKEN J S,EVANS A G.A microbend test method for measuring the plasticity length scale[J].Acta Materialia,1998,46(14):5109-5115.

[9] MINDLIN R D.Micro-structure in linear elasticity[J].Archive for Rational Mechanics & Analysis,1964,16(1):51-78.

[10]TOUPIN R A.Elastic materials with couple-stresses[J].Archive for Rational Mechanics and Analysis,1962,11(1):385-414.

[11]MINDLIN R D,TIERSTEN H F.Effects of couple-stresses in linear elasticity[J].Archive for Rational Mechanics and Analysis,1962,11(1):415-448.

[12]YANG F,CHONG A C M,LAM D C C,et al.Couple stress based strain gradient theory for elasticity[J].International Journal of Solids and Structures,2002,39(10):2731-2743.

[13]PARK S K,GAO X L.Bernoulli-Euler beam model based on a modified couple stress theory[J].Journal of Micromechanics and Microengineering,2006,16(11):2355.

[14]MA H M,GAO X L,REDDY J N.A microstructure-dependent Timoshenko beam model based on a modified couple stress theory[J].Journal of the Mechanics and Physics of Solids,2008,56(12):3379-3391.

[15]TSIATAS G C.A new Kirchhoff plate model based on a modified couple stress theory[J].International Journal of Solids & Structures,2009,46(13):2757-2764.

[16]TSIATAS G C,YIOTIS A J.A microstructure-dependent orthotropic plate model based on a modified couple stress theory[J].Recent Developments in Boundary Element Methods,A Volume to Honour Professor John T.Katsikadelis,2011,46(13):2757-2764.

[17]GUO J,CHEN J,PAN E.Size-dependent behavior of functionally graded anisotropic composite plates[J].International Journal of Engineering Science,2016,106:110-124.

[18]CHEN W,LI X.A new modified couple stress theory for anisotropic elasticity and microscale laminated Kirchhoff plate model[J].Archive of Applied Mechanics,2014,84(3):323-341.

[19]CHEN W,LI L,XU M.A modified couple stress model for bending analysis of composite laminated beams with first order shear deformation[J].Composite Structures,2011,93(11):2723-2732.

[20]CHEN W,LI X.Size-dependent free vibration analysis of composite laminated Timoshenko beam based on new modified couple stress theory[J].Archive of Applied Mechanics,2013,83(3):431-444.

[21]李莉，陈万吉，郑楠.修正偶应力理论层合薄板稳定性模型及尺度效应[J].工程力学,2013(5):1-7.

[22]YANG S,CHEN W.On hypotheses of composite laminated plates based on new modified couple stress theory[J].Composite Structures,2015,133:46-53.

[23]ASGHARI M,RAHAEIFARD M,KAHROBAIYAN M H,et al.The modified couple stress functionally graded Timoshenko beam formulation[J].Materials & Design,2011,32(3):1435-1443.

[24]矫桂琼，贾普荣.复合材料力学[M].西安：西北工业大学出版社,2008.

[25]IURLARO L,GHERLONE M,SCIUVA M D.Bending and free vibration analysis of functionally graded sandwich plates using the Refined Zigzag Theory[J].Journal of Sandwich Structures & Materials,2014,81(5):641.

(责任编辑：吴萍 英文审校：赵欢)

Staticbendingmodelofsize-dependentplaneorthotropicfunctionallygradedMindlinplate

HE Dan，YANG Zi-hao

(Key Laboratory of Liaoning Province for Composite Structural Analysis of Aerocraft and Simulation,Shenyang Aerospace University,Shenyang 110136,China)

A static bending model of size-dependent plane orthotropic functionally graded plate was proposed based on an anisotropic modified couple stress theory.The model included two orthogonal material length scale parameters,and thus can describe separately effects with different scale in orthogonal directions.The equilibrium equations and boundary conditions were deduced by the virtual work principle.The effects of scale effect on bending deflections were analyzed for a simply supported plate with a double sinusoidal load.Numerical results indicated that the scale effect was depicted well,and deflections calculated by the present model were smaller than those from the classical one.The scale effect was obvious as the geometry size approached the material length scale parameters,but it disappeared when the geometry size was much higher than those parameters.In addition,both grading index and span-to-thickness ratio have specific impacts on the scale effect.

modified couple stress theory;functionally graded material;orthotropic;scale effect;material length scale parameter

2017-05-12

国家自然科学基金(项目编号:11572204,11572081)

贺丹(1979-),辽宁沈阳人,副教授,博士,主要研究方向:微细观复合材料力学及结构优化,E-mail:Danhe@sau.edu.cn。

2095-1248(2017)04-0041-07

TB330.1

： A

10.3969/j.issn.2095-1248.2017.04.005