具有独立安装时间和恶化效应的单机成组排序问题研究
王吉波,赵伯来
(沈阳航空航天大学 理学院,沈阳 110136)
基础科学与工程
具有独立安装时间和恶化效应的单机成组排序问题研究
王吉波,赵伯来
(沈阳航空航天大学 理学院,沈阳 110136)
研究具有恶化效应且带有准备时间的单机成组排序问题,其中同一组内工件的加工时间具有简单线性恶化效应和独立的常数准备时间,各组之间的调整时间为独立的常数安装时间。目标是确定同一组内工件的排列顺序和各组之间的排列顺序使所有工件的最大完工时间最小。对此问题给出了一个下界和一个启发式算法,即上界,从而可以用分支定界算法来求此问题的最优解。
排序;单机;恶化效应;准备时间;分支定界算法
在经典排序中,假设工件的加工时间为常数,但在许多实际问题中,工件的加工时间可能与其开工时间有着某种联系。如在钢铁制造企业的连铸-轧制生产过程中,炼钢的基本单元是炉次,它是指同一座转炉一次共同冶炼的钢水。在炼钢的连铸阶段,高温熔融钢水在连铸机底部连续凝固成钢坯。当等待时间增加时(即加工开始时间延后),在连铸机上加工的炉次的温度将会降低,从而造成炉次加工时间的恶化(如刘鹏等[1])。具有恶化工件的这类问题在塑料工业、军事以及医疗等其他方面也有着广泛的应用(如Browne和Yechiali[2],Mosheiov[3-4],Ji和Cheng[5],Ng等[6],Sun等[7],Pei等[8])。关于工件加工时间具有恶化效应的综述,可参考文献Gawiejnowicz[9]。
随着市场竞争的日趋激烈,为适应多品种小批量生产方式的需求,成组技术成为排序问题研究领域中的一类热点问题。在成组排序问题中,工件可以分成“类似”工件的工件组。同组的工件连续加工时,不需要或需要较少的安装时间;不同组的工件接连加工时,需要一定的或需要较多的安装时间。柔性制造系统的发展给成组技术带来新的生机和活力,这是因为数控机床的高度柔性可以适应加工越来越多的不同种类的工件,避免和大大减少工件的安装时间,从而减少成本。近年来,国内外不仅重视成组技术的研究,更重视分组后组内工件的排序和组与组之间的排序。研究基于成组技术下的排序问题,对于提高柔性制造系统的生产能力具有重大的意义(如Potts和Van Wassenhove[10],Webster和Baker[11],唐国春等[12],Neufeld等[13])。
由以上两方面,很自然地会考虑具有恶化工件的成组排序问题。Wu等[14]研究了组内工件加工时间和组间安装(调整)时间都为恶化效应的排序问题,这里的恶化效应指的是加工时间(安装时间),是开工时间的简单函数。对最大完工时间问题和加权总完工时间问题,他们分别给出了多项式时间最优算法。Wang等[15]研究了组内工件加工时间和组间安装时间都为成比例线性恶化函数,对最大完工时间问题和加权总完工时间问题,他们同样给出了多项式时间最优算法。
Wu等[16]研究了组内工件加工时间和组间安装时间都为开工时间的线性恶化函数问题,其中组内工件恶化率相同,组间安装时间的恶化率也相同。对最大完工时间极小化问题,他们给出了多项式时间最优算法。对总完工时间极小化问题,他们证明了组内工件按基本加工时间的非减顺序排列,当各组工件个数相同时,能够得到多项式时间最优算法。对于各组内工件个数不同的总完工时间问题,他们猜测是NP-难的,并且给出了一个启发式算法。Wang等[17]研究了组内工件加工时间和组间安装时间都为一般线性函数的问题,目标函数为极小化最大完工时间,对这个问题,他们给出了多项式时间最优算法。Wei等[18]研究了组内工件加工时间和组间安装时间都为开工时间的简单恶化函数的排序问题,对加权完工时间平方和问题与加权等待时间平方和问题,他们分别给出了多项式时间最优算法。Lee等[19]研究了组内工件加工时间和组间安装时间都为开工时间的简单恶化函数的排序问题,对加权误工数问题,他们给出了一些优势性质,一个下界,一个启发式算法和分支定界法。并用数值例子进行了模拟,结果表明这个分支定界法非常有效。Wang等[20]研究了组内工件带有准备时间的简单线性恶化排序问题,其中组间的安装时间为独立的,即与开工时间无关。对最大完工时间极小化问题的一种特殊情况,他们给出了多项式时间最优算法。Xu等[21]研究了同Wang等[20]类似的问题,只是组内工件的加工时间为开工时间的成比例恶化函数。对最大完工时间极小化问题的一种特殊情况,他们给出了多项式时间最优算法,他们还对一般情况给出了启发式算法。
Wang等[20]研究的成果只是对一种特殊情况给出了多项式时间最优算法,但对于一般情况并没有给出什么结果,本文将继续研究Wang等[20]的排序模型,对最大完工时间极小化问题的一般情况将给出两个下界,从而提出分支定界精确算法。同时为了克服分支定界算法效率差的特性,提出了一个快速的启发式算法。
1 提出描述
假设有n个工件分别属于m个组,每一组Gi(1≤i≤m)中包含ni个工件{Ji1,Ji2,…,Jini},它们要在一台机器上进行加工,并假设第i组第j个工件(即工件Jij)的准备时间为rij(rij>0)。若工件Jij的开工时间为t,则其加工时间为
pij=αijt
(1)
其中αij是工件Jij的恶化率,此模型称为简单线性恶化函数。我们假设同组工件必须放在一起连续加工,每组都有一个独立的常数安装时间Si>0。令Cij表示工件Jij的完工时间,Cmax=max{Cij|i=1,2,…,m;j=1,2,…,ni}表示所有工件的最大完工时间。我们的目标是确定同组内工件的排列顺序和各组之间的排列顺序,使所有工件的最大完工时间最小(也就是机器的利用率最高),利用三参数表示法,这个排序问题可表示为1|rij,pij=αijt,Si,GT|Cmax,其中,1表示单机,GT表示成组技术(Group technology)。
2 启发式算法(上界)
引理1(Wang等[20]):
对于问题1|rij,pij=αijt,Si,GT|Cmax,如果各组之间的排列顺序已经给定,则在最优排序中把同组内的工件按照准备时间rij从小到大排序,即队组Gi,满足
ri(1)≤ri(2)≤…≤ri(ni),i=1,2,…,m,j=1,2,…,ni
(2)
引理2(Wang等[20]):


由引理1和引理2,我们可以给出如下的启发式算法,并作为分支定界法的上界。
启发式算法(HA)
(1)各组内的工件顺序按照准备时间从小到大排序ri(1)≤ri(2)≤…≤ri(ni),i=1,2,…,m。
(3)组间排序
①组间按照Si从小到大排序。



(4)选择①至④目标函数值最小的排序为解。
3 下界
分支定界法的有效性受它下界的影响是很大的,下面我们将给出确定下界的方法。设前k组为已经确定的排序,未排序的工件组有m-k组。已经排序的部分称之为序列PS,未排序的部分称之为序列US,π是一个通过US追加PS获得的完整的序列;即π=(PS,US)。
根据成组恶化模型,在序列π中第(k+1)组最后工件的完工时间为

(3)
类似地,在序列π中第(k+2)组最后工件的完工时间为
αk+2(l))

αk+2(l))
同理可得:在序列π中第m组工件的完工时间满足

(4)
因此,序列π的最大完工时间满足条件
(5)
引理3:对于表达式α1α2α3…αm-1αm+α2α3…αm-1αm+…+αm-1αm+αm,若要其取得最小值,则需将αi按非增的顺序进行排列,即α1≥α2≥α3≥…≥αm。反之,将αi按非减的顺序进行排列,则可以得到该表达式的最大值。
证明:用相邻交换法很容易证明。
同理可推广得到:若满足α1≥α2≥α3≥…≥αm且S=min{S1,S2,S3…Sm}可得到表达式S1α1α2α3…αm+S2α2α3…αm+…+Smαm≥Sα1α2α3…αm+Sα2α3…αm+…+Sαm的最小值。根据引理3和公式(5)可得出第一个下界LB1:

(6)

根据式(3),在序列π中第(k+1)组最后工件的完工时间为

(7)

同理可得:在序列π中第m组工件的完工时间满足
(8)
因此,根据公式(7)和(8)可得出第二个下界LB2。

(9)

为了得到更好的下界,我们取LB1和LB2的最大值,即
LB=max{LB1,LB2}
(10)
接下来我们举个例子来帮助更好地理解分支定界法及下界。

解:启发式算法(HA):
(1)组内工件排序按照rij从小到大排序得
G1:[J12→J11],G2:[J23→J22→J21],G3:[J31→J33→J32];G4:[J42→J41]

(3)组间排序
①组间按照Si从小到大排序得G1→G2→G3→G4,Cmax=3 939。
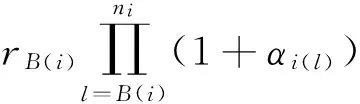


(4)选择①至④目标函数值最小的排序为解,即G2→G3→G4→G1,Cmax=968(上界)。
则根据上文提到的计算下界的方法我们可以得到分支过程,如图1所示。
图1中内的数字代表计算出的下界的值,如果定义组G0为第零层的话,那么第一层最左侧组G1旁边的数字3 918就代表组G1固定的下界,计算过程如下:
由于组G1固定,那么根据公式(6)及公式(9)给出的计算下界方法得:

图1 分支定界法过程
α(l))
=16×18×4×3+2×18×4×3+2×4×3+2×3=3 918


因为LB=max{LB1,LB2},所以LB=3 918,即G1固定的下界为3 918。其余下界的计算过程类似,在此不再一一列出。从图1可以看出,最优排序为G2→G1→G3→G4,最优值为Cmax=939。
4 结论
本文研究了工件具有恶化效应和准备时间的单机成组排序问题,其中组和组之间有一个独立的安装(调整)时间。目的是求组内工件和组间工件的加工顺序,并使最大完工时间(时间表长)最小,本文结合下界和上界给出了一个分支定界算法,从而能求出该问题的一个最优排序,并给出相应的例子来说明分支定界算法(包括上界和下界)的计算过程。本文只是研究单机简单线性恶化函数情况下的成组排序问题,可以将其延伸到平行机或流水作业等多机排序问题;加权完工时间和等复杂的目标函数;或者考虑更一般的恶化函数的情况。
[1] 刘鹏,周晓晔,衣娜.带有减少线性恶化效应的双代理调度问题[J].系统工程学报,2011,26(3):387-392.
[2] BROWNE S,YECHIALI U.Scheduling deteriorating jobs on a single processor [J].Operations Research,1990,38(3):495-498.
[3] MOSHEIOV G.V-Shaped policies to schedule deteriorating jobs [J].Operations Research,1991,39:979-991.
[4] MOSHEIOV G.Scheduling jobs under simple linear deterioration [J].Computers and Operations Research,1994,21(6):653-659.
[5] JI M,CHENG T.C.E.Batch scheduling of simple linear deteriorating jobs on a single machine to minimize makespan [J].European Journal of Operational Research,2010,202(1):90-98.
[6] NG CT,WANG J-B,CHENG T C E,et al.Flowshop scheduling of deteriorating jobs on dominating machines [J].Computers & Industrial Engineering.2011,61(3):647-654.
[7] SUN L-H,SUN L-Y,WANG M-Z,et al.Flow shop makespan minimization scheduling with deteriorating jobs under dominating machines [J].International Journal of Production Economics,2012,138(1):195-200.
[8] PEI J,PARDALOS PM,LIU X,et al.Serial batching scheduling of deteriorating jobs in a two-stage supply chain to minimize the makespan [J].European Journal of Operational Research,2015,244(1):13-25.
[9] GAWIEJNOWICZ S.Time-dependent scheduling [M].Berlin Springer,2008.
[10]POTTS CN,VAN WASSENHOVE LN.Integrating scheduling with batching and lot-sizing:a review of algorithms and complexity [J].Journal of Operational Research Society 1992,43(5):395-406.
[11]WEBSTER S,BAKER KR.Scheduling groups of jobs on a single machine [J].Operations Research,1995,43(4):692-703.
[12]唐国春,张峰,罗守成,等.现代排序论[M].上海:上海科学普及出版社,2003.
[13]NEUFELD JS,GUPTA JND,BUSCHER U.A comprehensive review of flowshop group scheduling literature [J].Computers and Operations Research,2016,70(C):56-74.
[14]Wu CC,SHIAU YR,LEE WC.Single-machine group scheduling problems with deterioration consideration [J].Computers and Operations Research,2008,35(5):1652-1659.
[15]WANG J-B,LIN L,SHAN F.Single machine group scheduling problems with deteriorating jobs [J].International Journal of Advanced Manufacturing Technology 2008,39(7-8):808-812.
[16]WU CC,LEE WC.Single-machine group-scheduling problems with deteriorating setup times and job-processing times [J].International Journal of Production Economics,2008,115(1):128-133.
[17]WANG J-B,GAO W-J,Wang L-Y,et al.Single machine group scheduling with general linear deterioration to minimize the makespan [J].International Journal of Advanced Manufacturing Technology 2009,43(1-2):146-150.
[18]WEI C-M,WANG J-B.Single machine quadratic penalty function scheduling with deteriorating jobs and group technology [J].Applied Mathematical Modelling,2010,34(11):3642-3647.
[19]LEE W-C,LU Z-S.Group scheduling with deteriorating jobs to minimize the total weighted number of late jobs [J].Applied Mathematics and Computation,2012,218(17):8750-8757.
[20]WANG J-B,HUANG X,WU Y-B,et al.Group scheduling with independent setup times,ready times,and deteriorating job processing times [J].International Journal of Advanced Manufacturing Technology 2012,60(5-8):643-649.
[21]XU Y-T,ZHANG Y,HUANG X.Single-machine ready times scheduling with group technology and proportional linear deterioration [J].Applied Mathematical Modelling 2014,38(1):384-391.
(责任编辑:刘划 英文审校:刘勇进)
Researchonsingle-machinegroupschedulingwithindependentsetuptimesanddeteriorationeffect
WANG Ji-bo,ZHAO Bo-lai
(College of Science,Shenyang Aerospace University,Shenyang 110136,China)
This paper considers a single-machine group scheduling problem with deterioration effect and ready times,where the processing time of a job within each group is a simple linear deterioration effect,ready time of a job within each group is an independent constant,and the setup times of groups are independent constants.Our objective is to determine the schedule of jobs within each group and the schedule of groups to minimize the make-span.A branch-and-bound algorithm incorporating with a lower bound and a heuristic algorithm(i.e.,an upper bound) are proposed to find the optimal solution for the problem.
scheduling;single-machine;deterioration effect;ready time;branch-and-bound algorithm
2017-05-31
国家自然科学基金项目(项目编号:71471120),沈阳航空航天大学大学生创新创业训练计划项目(项目编号:X1611405)
王吉波(1975-),男,辽宁沈阳人,教授,博士后,主要研究方向:生产计划与排序,E-mail:wangjibo75@163.com。
2095-1248(2017)04-0082-06
O223;C934
: A
10.3969/j.issn.2095-1248.2017.04.011

