静态中立体带电导体电荷分布概率的计算及趋肤效应的诠释

北京北方长城光电仪器有限公司 徐卫星

静态中立体带电导体电荷分布概率的计算及趋肤效应的诠释

北京北方长城光电仪器有限公司 徐卫星

为了能够了解导体内电荷的分布概况,利用麦克斯韦方程组中电场积分式,令其电场强度与闭环回路(或封闭空间)的积分和为零的理念,建立坐标模型和数学模型进行运算求得分布概率结果所采用的一种方法。

麦克斯韦方程积分式；库仑定律；导体内电场强度处处为零；电荷分布概率；趋肤效应

引言

上两篇论文阐述了对线性带电导体电荷分布概率的计算方法(发表在《电子技术与软件工程》2016年16期第138页 国际刊号ISSN 2095-5650)和对平面带电导体电荷分布概率的计算方法(发表在《电子世界》2017年9月期刊 国际刊号ISSN 1003-0522)本次继续论述关于立体导体电荷分布概率的计算。

1.为了更好地描述这种方法先阐述几个基本概念

1.1 立体分割：将带电导体分割成n×m×l多个边长为2△正方形小块体。

1.2 中心电荷条（线）：将条状带电体分割成n×m多个边长为2△条形状。

1.3 单端电源：导体一端或两端与具有电势（位）单电源体的连接。（会形成电荷的静态分布）

1.4 双端电源：导体两端与具有不同电势（位）两个电源体的连接。（会形成电流）

1.5 多端电源：导体多处与两个以上具有不同电势（位）多个电源体的连接。（会形成电流）

1.6 趋肤时间Th：从电开通到形成电密度一致均匀电流的时间。

1.7 外电场：除导体自身电荷作用以外其它电源电场的作用。

1.8 外层面：带电导体相对于外电场力方向所有垂直平面的边缘环线。

2.证明论述

2.1 计算方法：将任意立体的带电导体分割出n×m×l多个小正方体。(一般边长是2△的正方体)将n×m×l多个凡是存有电荷小正方体中的电荷量，集中在选定的各自小正方体中的中心电荷点处。n×m×l多个中心点电荷的相互电场力可利用库仑定律建立函数关系。再经过合力分解方法转化为三条互相垂直的线性上，令其处处为零。解出各小正方体的电荷量，从而求得各自密度值。

2.2 计算步骤：在任意立体的带电导体中任意分割出厚为2△的片，在片上任意分割二条垂直于片平面间距为2△的平行面，在二平行面中取n多个边长2△的正方体，左右外延直至导体的边缘。将二平行面以同样方法前后外延m多个平行面，直至导体的边缘，将片平面以同样方法上下外延直至导体的边缘。并取得n×m×l个边长2△的正方体。在含有导体的小正方体中心确定中心电荷点。（因导体往往处于不规则形状，会有小正方体中没有导体存在）利用库仑定律建立出每个中心电荷点相互作用力的关系，并分解为水平纵向分量、水平横向分量和垂直分量。建立测试点使其各自为零。推算出各个电荷量，便求得电荷分布概率。即：

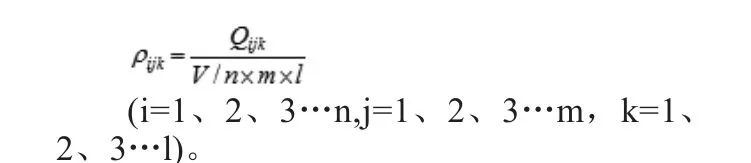
式中ρijk为电荷体密度，Qijk为中心电荷点电量，V为导体体积。

2.3 可行性论证：在立体导体中任取一个分割小体积，此处为某一小正方体。如图1当求得测试点q1、q2、q3、…q12、都为零时q0测试点处必为零。其它小正方体具有同理。而当n→∞，m→∞，l→∞，△→0时，因导体是连续、电荷分布是连续，所以任意点处在平衡状态下是无电场力和电荷移动的存在，任何闭环的积分必为零。

图1

3.举例

为了更好地理解这种方法，下面举几个简单而有特性的例子。

3.1 扁正方体带电导体

3.1.1 环境与条件：

一块边长为4△×6△×6△的正方体带有QS电量的导体，在没有任何电磁场干扰的理想情况下计算电荷分布概率。

3.1.2 阐述：

将带有电荷导体分割为n=3，m=3，l=2，边长为2△的18个小正方体。如图2,其中Q111、Q112、Q113、Q121、Q122、Q123、Q131、Q132、Q133、Q211、Q212、Q213、Q221、Q222、Q223、Q231、Q232、Q233为中心电荷点，q111y、q112y、q121y、q122y、q131y、q132y、q211y、q212y、q221y、q222y、q231y、q232y为水平横向测试点，q111x、q112x、q121x、q122x、q131x、q132x、q211x、q212x、q221x、q222x、q231x、q232x为水平纵向测试点。

Q11z、q12z、q13z、q21z、q22z、q23z，q31z、q32z、q33z为垂直测试点。

例如：Q111对测试点q132y的电场作用力根据库仑定律为：

（K为库仑常量，q为测试点电量，Q111为中心电荷点电量，r为Q111与q132y的距离），即：

其水平分量为：

以此类推。

3.1.3 图例：

为了观察清晰只画一部分

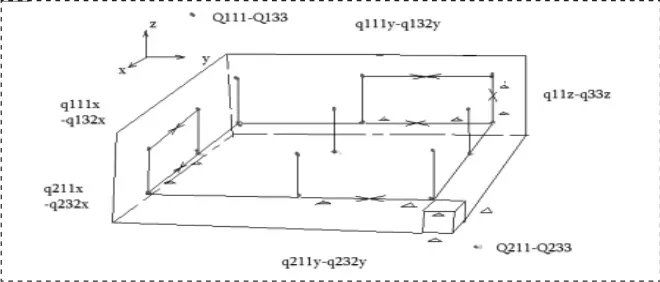
图2

3.1.4 根据图示和运算方法建立数学模型：

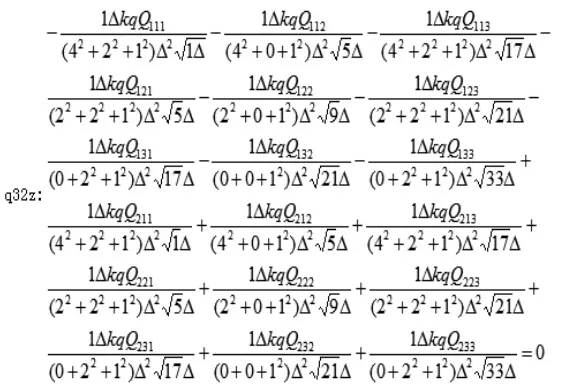
3.1.5 运算结果：约去△、K、q解得：

3.2 柱形体带电体：

3.2.1 环境与条件：有一条4△×6△长度很长的柱形带电导体。在没有任何电磁场干扰的理想情况下，为了便于计算在柱状导体轴向上只取2△长度中存储电荷量QS0来加以计算，进行密度的相对比较。

3.2.2 阐述：如图3，从第一篇论文中可知非常大平面导体其中部电荷密度值是一样的，因此可以认为在很长的柱状导体中轴向方向每条平行条上电荷密度是一致的。而径向长度只有4△和6△长,所以径向电荷会有很大的变化。在此将柱状带电导体分割为n=3，m=2条边长2△×2△条状体,建立6个中心电荷条（线）ρQi(i=1、2、3、4、5、6)和7个测试点q14、q25、q36、q12、q23、q45、q56，l为测试点到中心电荷条的距离，A为测试点到电荷点dQi的距离，ρQi为中心电荷条的密度。

由于轴向电荷密度一致，将中心电荷点改用中心电荷条，采用积分的方法将条上各个电荷点对测试点的电场径向作用力进行积分并令其各个为静态，可求得电荷分布概率。

对于中心电荷条上每个电荷点ρQi2△dt(i=1、2、3、4、5、6)对测试点q的径向作用力为：

将(3-2)代入(3-1)得：

对式(3-3)进行2倍0-90度的积分。

3.2.3 图例：

图3

3.2.4 根据图示和运算方法建立数学模型：

3.2.5 运算结果：约去△、K、q，解得：

3.3 球形带电体：

如图4在球形静态导体中任取一点A，在过A点直径的切平面上电场力为零时，必然存在这么一种情况，在球内有无数个相对于此直径的对称点，其对称点中的电荷密度分别必相等。在此条件下必然存在切面方向的静态平衡。而当某一趋近于此直径的对称点如B、C两点若Qb点要等于Qc则ρb必等于ρc。(导体为连续的电荷分布也是连续的)由于对称性的球形，直径与B、C两点可存在于以圆心为轴心的任何球内地方，所以同半径的球形曲面中的电荷密度是相等的。也同时证明此直径的所有对称点的电荷密度也是分别相等的。而直径方向电荷密度的变化在上一篇论文圆平面的计算证明边缘密度大于中心的，同样球表面的电荷密度也是大于球心的，由于球体计算十分复杂这里就不阐述了。

图4

4.对趋肤效应的诠释

在外电场开始作用的瞬间，由于静态平衡导体外层面的电流密度必定很大，而中心会很小。而双端源两个端头的电势不同，电荷密度的分布会有很大的差异，而带电导体根据自身所带容余电荷的不同（或是电子或是空穴）使其端头的边缘、中心与双源两端头边缘、中心产生不同电势差，而且会使一端电势差比另一端要大（或小）特别是在外层面上，在极短的时间内使得导体外层面流入流出的电荷量大但不相等。这会使外层面的电荷密度下降，当最外层面的电荷密度下降到与次外层电荷密度一样时，最外层面的电荷与次外层电荷会产生共同变化。成为导体内电流密度最大、流入流出此层面电荷差值最大，电荷密度下降最快。同样继续达到更次外层面电荷密度后又与更次外层面电荷共同变化，依此类推。外层面电流厚度逐渐增加直到与中心电荷密度相同。电流才均匀分布在整个横截面上。

这个过程再快也是需要时间。如果是直流或低频交流即周期T＞Th时导体会成为均匀的电阻体，而当T≤Th时只有外层面和其它次外层面成为导体。（即不均匀的电阻体）当T〈〈Th导体会成为非常非常薄外层面的导电体。

在变化过程中会不会产生静态分布状态?答案是不会的。因为在外电场力作用下无法产生。如图5，当A区域电荷在垂直外电场力的平面上移到B区域，使B区域电荷密度高于周围区域时，很快在外电场力作用下使的流进B区域电荷少于流出的量。直到B区域电荷密度与周围区域一样为止。A区域也是同样道理。

图5

当双端电源为交流时，两端电势的高低是交替互换的，当两端电势差为零时，会形成单端效果即导体形成静态分布状态。周而复始，产生了趋肤效应的机理。

5.结束语

通过上述的论证得到了以下结果：

5.1 带电导体中心与表面的电荷密度值是不相等的，离中心区域越远密度越高。

5.2 处于静态平衡的带电导体，由于电荷密度分布不均匀，在其内部不同位置形成的电势（位）也不同。

5.3 从不同的角度诠释了趋肤效应，同样也在验证此论证推理的实际效果。

有不对之处请多指正。

[1]迪派克(Dipak,L．S)唯迪斯(Valdis,V．L)著;沈远茂等译．应用电磁学与电磁兼容[M]．北京:机械工业出版社,2009．

[2]汪泉弟,张淮清．电磁场[M]．北京:科学出版社,2013．

[3]张洪欣,沈远茂,韩宇南．电磁场与电磁波[M]．北京：清华大学出版社,2013．

[4]付云起,张光甫,莫锦军,吴微微．天线理论与工程[M]．北京:电子工业出版社,2015．

徐卫星（1957-），高级工程师，主要研究方向：电气测量。