基于反射波动方程的叠前地震反射数据波阻抗相对变化成像研究

陈生昌,周华敏

(1.浙江大学地球科学学院,浙江杭州310027;2.长江水利委员会长江科学院,湖北武汉430010)

基于反射波动方程的叠前地震反射数据波阻抗相对变化成像研究

陈生昌1,周华敏2

(1.浙江大学地球科学学院,浙江杭州310027;2.长江水利委员会长江科学院,湖北武汉430010)

波阻抗是地震数据岩性处理解释中的重要参数。提出了一种基于反射波动方程的叠前地震反射数据深度域波阻抗相对变化成像方法。从变密度的声波方程出发,首先利用高频近似,推导出基于波阻抗相对变化的一次反射波场的线性传播方程,然后基于该传播方程,利用线性反演理论推导出获得深度域波阻抗相对变化近似估计的成像公式。受反射地震数据频带范围的限制和波形线性反演问题近似求解成像方法的限制,该波阻抗相对变化成像方法所获得的成像结果的保真性和分辨率会存在不足,但其计算量与逆时偏移的计算量基本相当。合成数据的模型试验结果验证了波阻抗相对变化成像方法的有效性。

叠前地震反射数据;高频近似;反射波动方程;线性反演;波阻抗相对变化;成像

波阻抗是联系地质与反射地震数据的一个重要的物性参数,在油气地震勘探开发的数据处理解释中,特别是在岩性油气藏勘探开发中,发挥了十分重要的作用[1-2]。因此,波阻抗反演在地震数据处理中具有特殊的地位。

自20世纪70年代初LAVERGNE[3]首先提出波阻抗反演方法以来,有关波阻抗反演方法技术的研究有了很大的发展,提出了各种不同的波阻抗反演方法。如叠前地震数据波阻抗反演和叠后地震数据波阻抗反演。在叠前地震数据波阻抗反演方法中,有基于Zoeppritz方程近似的弹性波阻抗反演方法[4-5]和全波形反演方法[6-8]。在叠后地震数据波阻抗反演方法中,有直接反演方法[9]、基于模型反演方法[10-13]和非线性反演方法[14-15]。叠前地震数据波阻抗反演尽管计算复杂、计算量大,而且对数据的要求也高,但可以得到相对多的地层信息,特别是基于全波形的波阻抗反演,不仅可以充分利用地震数据的波形信息,还可以适应地下介质的横向变化。因此叠前地震数据波阻抗反演是波阻抗反演的发展趋势。叠后地震数据波阻抗反演是当前生产中比较常用的方法技术,计算效率高,但由于地震数据叠加处理方法技术本身存在的不足,叠后地震数据波阻抗反演在复杂地区的应用受到限制。

反射地震波是地下波阻抗变化产生的,ZHANG等[16]提出了一种利用真振幅逆时偏移估计地下波阻抗扰动的方法,并认为在角度域共成像点道集中的小角度成像波场信息反映了波阻抗的扰动,为利用波动方程偏移方法技术进行地下波阻抗成像提供了思路,但是他们的地下波阻抗扰动估计方法是通过对偏移方法中成像公式的改造得到,而不是根据与波阻抗有关的反射波场传播方程得到。基于波动方程的逆时偏移对地下介质模型空间变化具有很好的适应性[17-22]。与其它偏移成像方法一样,当前的逆时偏移也是基于CLAERBOUT[23]所提出的偏移成像原理,并认为对偏移成像结果进行积分就可以实现对波阻抗的成像[24]。CLAERBOUT偏移成像的核心思想是其提出的“时间一致性成像原理和成像公式”,我们认为其成像原理仅是一个有关地震波传播旅行时的概念性描述,成像公式缺乏严格的数学物理推导,也不满足描述地震波传播的数学物理方程。陈生昌等[25]将地震数据偏移成像定义为近似求解地震数据的波形线性反演问题,由地震波所满足的波动方程,利用高频近似给出了反射面上反射率的定义,进而推导出了基于反射率分布的反射波传播方程,然后在反射波传播方程的基础上应用线性反演的方法对地震数据偏移成像进行了重新推导,建立了对地下反射率进行成像的偏移成像公式,为基于地震波场传播方程的偏移成像方法研究与应用提供了坚实的理论基础。

根据文献[25]对偏移成像的重新定义与推导,本文在变密度声波方程的基础上,首先应用地震波传播的散射理论和地震波方法理论中的高频近似,推导出基于波阻抗相对变化的一次反射地震波线性传播方程,然后再应用线性反演的方法推导出波阻抗相对变化的成像公式,最后将提出的波阻抗成像方法应用于简单的层状介质模型和Marmousi模型的合成地震数据,均取得了理想的结果。

1 方法原理

我们采用变密度声波方程描述地震波传播:

(1)

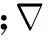
(2)

将方程(1)和方程(2)变换到频率域,分别得到:

式中:ω表示频率;F(ω)为f(t)的傅里叶变换;G(x,ω;xs)和P(x,ω;xs)分别为g(x,t;xs)和p(x,t;xs)的傅里叶变换。

1.1 基于波阻抗相对变化的反射波动方程

为了构建反射地震数据的波阻抗相对变化成像方法,首先要推导出基于波阻抗相对变化的反射波动方程。

令v0(x)和ρ0(x)分别为v(x)和ρ(x)的背景速度模型和背景密度模型,则它们的相对扰动分别为:

(5)

将(5)式代入方程(3)可得到由相对扰动引起的散射波场传播方程:

(6)

式中:Ps(x,ω;xs)为速度和密度相对扰动产生的散射波场;P(x,ω;xs)表示总波场,有P(x,ω;xs)=Pi(x,ω;xs)+Ps(x,ω;xs),其中,Pi(x,ω;xs)表示背景速度和密度模型下的波场,也称为背景波场或入射波场,有:

(7)

假定v0(x)和ρ0(x)为光滑的背景模型,则方程(7)中的Pi(x,ω;xs)仅包含直达波和透射波,而不包含散射波和反射波。

在一阶Born近似下,对于方程(6)有:

(8)

将方程(8)返回到时间域,并利用形如方程(2)背景模型中的Green函数将其写为积分形式,有:

(9)

式中:v0(y)和ρ0(y)为光滑的背景模型;g(x,t;y)为背景模型中描述散射波传播的Green函数;“*”代表时间褶积。经推导与简化[7],方程(9)可写为:

(10)

将方程(10)写为频率域形式,有:

(11)

(12)

进一步化简,有:

(13)

式中:Pr(x,ω;xs)为高频近似下由地下速度、密度相对扰动产生的反射波场。

令:

(14)

根据波阻抗定义I(y)=v(y)ρ(y),对于背景模型有I0(y)=v0(y)ρ0(y),波阻抗扰动有δI(y)=δ·[v(y)ρ(y)]=ρ(y)δv(y)+v(y)δρ(y)。对于法向入射α=0,有:

(15)

式中:Ir(y,α=0)为法向入射时的波阻抗相对扰动。由(14)式可知,Ir(y,α)是一个随半开角α变化的波阻抗相对扰动。随着α的增大,Ir(y,α)由阻抗型相对扰动逐渐转变为速度型相对扰动。当α=π/2时,有:

(16)

将(14)式代入方程(13),有:

(17)

将(17)式写为时间域形式,有:

(18)

方程(17)和方程(18)分别为高频近似条件下基于波阻抗相对变化的反射波动方程的频率域形式和时间域形式。

1.2 基于反射波动方程的深度域波阻抗相对变化成像

1.1节在高频近似条件下得到的基于波阻抗相对变化的反射波动方程(17)、(18)是利用反射波地震数据对地下波阻抗相对变化进行反演和成像的基础。我们将成像定义为基于正演算子的伴随算子的近似反演(或称为粗糙反演)。相对于基于逆算子的反演,利用成像得到的解的估计通常会存在保幅性差、分辨率低的问题。

利用背景介质模型下的Green函数,方程(7)中的入射波场可表示为:

(19)

在光滑背景模型的假定下,根据方程(17),对于炮点xs激发,检波点xg接收的反射波地震数据Dr(xg,ω;xs)可表示为:

(20)

根据陈生昌等[26]提出的时间二阶积分波场的全波形反演方法,方程(20)可写为:

(21)

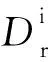
令:

(22)

得到:

(23)

将线性积分方程(23)写为矩阵形式,有:

(24)

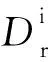
(25)

式中:W-g代表W的最小二乘广义逆矩阵;W*为W的伴随矩阵。

将(25)式求得的m和方程(19)得到的入射波场Pi(x,ω;xs)代入(22)式,可得到波阻抗相对变化的估计:

(26)

式中:Re表示取实部运算。

考虑到(25)式计算的稳定性和逆矩阵计算的复杂性,我们用伴随矩阵W*代替(25)式中的最小二乘广义逆矩阵W-g:

(27)

(27)式的运算实质上是对波场数据u的伴随传播(反向传播)。

再考虑(26)式中波场相除运算的不稳定性问题,并结合(27)式将(26)式改写为:

(28)

式中:“*”代表复共轭运算。

(19)式、(27)式和(28)式为波阻抗相对变化在角度α上的近似求解,实质上实现了对Ir(x,α)的成像。将上述对Ir(x,α)的成像运算转换到时间域。

1) 地下入射波场的计算(对应公式(19)所表示的运算):

(29)

2) 地下时间二阶积分反射波场的伴随(逆时)重建(对应公式(27)所表示的运算):

(30)

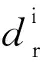
3) 对波阻抗相对变化Ir(x,α)的成像(对应公式(28)所表示的运算):

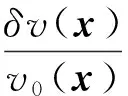
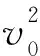
(31)

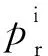
(32)

对于不考虑地下介质密度变化的标量波动方程,则可得到基于速度相对变化vr(x,α)的反射波动方程,有vr(x,α)=av(x)cos2α=2δv(x)cos2α/v0(x),相应地得到对速度相对变化的成像,对应的计算公式如下。

1) 地下入射波场的计算:

(33)

2) 地下时间二阶积分反射波场的伴随(逆时)重建:

(34)

3) 对速度相对变化vr(x,α)的成像:

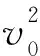
(35)

2 数值试验

为了验证上述基于反射波动方程提出的叠前地震反射数据波阻抗相对变化成像方法的正确性与有效性,我们采用两个二维模型的合成数据进行试验。由于在模型试验中没有考虑密度的变化,因此试验得到的波阻抗相对变化成像结果实际是速度相对变化的成像结果。

2.1 简单模型试验

图1显示了简单层状模型的速度分布,在速度值为3000m/s的均匀背景中包含一个低速层和一个高速层,上部低速层的速度值为2500m/s,下部高速层的速度值为3500m/s。在该速度模型上进行地震数据数值模拟,得到试验所需的合成地震反射数据。将本文所提出的波阻抗相对变化成像方法应用于简单模型的合成地震反射数据,得到图2所示的速度相对变化成像结果。图3为图2红框中速度相对变化成像结果的波形放大图。

对比图1和图2可以看出,波阻抗相对变化成像方法所得到的波阻抗相对变化成像结果中的低阻层和高阻层与模型中的低速层和高速层在空间位置和相对幅值变化方面都对应很好,验证了本文所提出的波阻抗相对变化成像方法的正确性。

2.2 Marmousi模型试验

Marmousi模型地震反射数据是检验波动方程叠前深度偏移成像算法的标准模型数据。Marmousi模型数据共有240炮,每炮96个接收道,炮间距25m,道间距25m,记录长度3s,时间采样率4ms。

图1 简单模型的速度分布

图2 简单模型的速度相对变化成像结果

图3 图2红框中的波形放大显示

图4显示了Marmousi模型的速度相对变化。图5 为利用本文提出的波阻抗相对变化成像方法得到的速度相对变化成像结果。为了对比,我们还利用逆时偏移方法对Marmousi模型数据进行了构造偏移成像,图6为由逆时偏移得到的构造成像结果。

对比图4,图5和图6可以看出,由波阻抗相对变化偏移成像方法得到的速度相对变化成像结果能更清楚地反映地下岩性的变化,而由逆时偏移得到的构造成像结果主要反映地下构造界面的几何结构。

图4 Marmousi模型的速度相对变化分布

图5 Marmousi模型的速度相对变化成像结果

图6 Marmousi模型的逆时偏移成像结果

3 结论

地震反射数据成像是一种基于反射波动传播方程的波形线性反演问题的近似求解。建立基于波阻抗相对变化的反射波动方程,通过线性反演方法提出的利用逆时传播的深度域波阻抗相对变化成像方法是对地震数据反射率成像方法的推广,可为进一步的岩性成像方法研究打下基础。本文方法的计算量与当前常用的逆时偏移成像方法的计算量基本相当,仅增加了计算量非常少的反射地震数据时间二阶积分计算。与当前对反射面空间位置和反射率变化进行成像的偏移成像方法不同,本文提出的波阻抗相对变化成像方法可对地下波阻抗的相对变化进行成像,可为地震数据的岩性处理解释提供基础数据。

[1] 李庆忠.走向精确勘探的道路——高分辨地震勘探系统工程剖析[M].北京:石油工业出版社,1993:1-196 LI Q Z.The way to obtain a better resolution in seismic prospecting:a systematical analysis of high resolution seismic exploration[M].Beijing:Petroleum Industry Press,1993:1-196

[2] 李庆忠.岩性油气藏地震勘探若干问题讨论(Ⅰ)[J].岩性油气藏,2008,20(2):1-6 LI Q Z.Discussion on seismic exploration of lithologic reservoirs(Ⅰ)[J].Lithologic Reservoirs,2008,20(2):1-6

[3] LAVERGNE M.Pseudo-diagraphics de vitesse en offshore profound[J].Geophysical Prospecting,1975,23(4):695-711

[4] CONNOLLY P.Elastic impedance[J].The Leading Edge,1999,18(4):438-452

[5] WHITECOMBE N.Elastic impedance normalization[J].Geophysics,2002,67(1):60-62

[6] LAILLY P.The seismic inverse problem as a sequence of before stack migrations[J].Expanded Abstracts of Conference on Inverse Scattering,Theory and Application,Society for Industrial and Applied Mathematics,1983:206-220

[7] TARANTOLA A.Inversion of seismic reflection data in the acoustic approximation[J].Geophysics,1984,49(8):1259-1266

[8] VIRIEUX J,OPERTO S.An overview of full-waveform inversion in exploration geophysics[J].Geophysics,2009,74(6):WCC1-WCC26

[9] LINDSETH O.Synthetic sonic logs:a process for stratigraphic interpretation[J].Geophysics,1979,44(1):3-26

[10] COOKE D A,SCHNEIDER W A.Generalized linear inversion of reflection seismic data[J].Geophysics,1983,48(6):665-676

[11] OLDENBURG D W,SCHEUER T,LEVY S.Recovery of the acoustic impedance from reflection seismograms[J].Geophysics,1983,48(10):1318-1337

[12] 杨文采.地震道的非线性混沌反演I:理论和数值试验[J].地球物理学报,1993,36(2):222-232 YANG W C.Nonlinear chaotic inversion of seismic traces I:theory and numerical experiments[J].Chinese Journal of Geophysics,1993,36(2):222-232

[13] 杨文采.地震道的非线性混沌反演Ⅱ:关于Lyapunov指数和吸引子[J].地球物理学报,1993,36(3):376-387 YANG W C.Nonlinear chaotic inversion of seismic traces Ⅱ:about Lyapunov exponent and attractor[J].Chinese Journal of Geophysics,1993,36(3):376-387

[14] ROGERS S T,FANG J H,KARR C L,et al.Determination of lithology from well logs using a neural network[J].AAPG Bulletin,1992,76(5):731-739

[15] 杨立强,宋海滨,郝天珧.基于BP神经网络的波阻抗反演及应用[J].地球物理学进展,2005,20(1):34-37 YANG L Q,SONG H B,HAO T Y.Application of impedance inversion based on BP neural network[J].Progress in Geophysics,2005,20(1):34-37

[16] ZHANG Y,DUAN L,ROBERTS G.True amplitude reverse time migration:from eflectivity to velocity and impedance perturbations[J/OL].[2016-10-01].http:∥www.cgg.com/technicalDocuments/cggv_0000014832.pdf

[17] HEMON C.Wave equations and models[J].Geophysical Prospecting,1978,26(4):790-821

[18] BAYSAL E,KOSLOFF D,SHERWOOD J.Reverse time migration[J].Geophysics,1983,48(11):1514-1524

[19] MCMECHAN G.Migration by extrapolation of time-dependent boundary values[J].Geophysical Prospecting,1983,31(3):413-420

[20] WHITMORE D.Iterative depth migration by backward time propagation[J].Expanded Abstracts of 53rdAnnual Internat SEG Mtg,1983:382-385

[21] ETGEN J,GRAY S,ZHANG Y.An overview of depth imaging in exploration geophysics[J].Geophysics,2009,74(6):WCA5-WCA17

[22] LEVEILLE J,JONES I,ZHOU Z,et al.Subsalt imaging for exploration,production,and development:a review[J].Geophysics,2011,76(5):WB3-WB20

[23] CLAERBOUT J.Toward a unified theory of reflector mapping[J].Geophysics,1971,36(3):467-481

[24] ROBEIN E.Seismic imaging:a review of the techniques,their principles,merits and limitations[M].Houten:EAGE Publications,2010:1-244

[25] 陈生昌,周华敏.再论地震数据偏移成像[J].地球物理学报,2016,59(2):643-654 CHEN S C,ZHOU H M.Re-exploration to migration of seismic data[J].Chinese Journal of Geophysics,2016,59(2):643-654

[26] 陈生昌,陈国新.时间二阶积分波场的全波形反演[J].地球物理学报,2016,59(10):3765-3776 CHEN S C,CHEN G X.Full waveform inversion of the second-order time integral wavefield[J].Chinese Journal of Geophysics,2016,59(10):3765-3776

(编辑：陈 杰)

Arelativeimpedancevariationimagingofpre-stackseismicreflectiondatabasedonreflectionwaveequation

CHEN Shengchang1,ZHOU Huamin2

(1.SchoolofEarthSciences,ZhejiangUniversity,Hangzhou310027,China;2.ChangjiangRiverScientificResearchInstituteofChangjiangWaterResourcesCommission,Wuhan430010,China)

Impedance of subsurface media is an important parameter for lithologic processing and interpretation of seismic data.In this paper,a relative impedance variation imaging in depth domain based on the reflection wave equation is proposed.Starting from the variable density acoustic wave equation,the proposed method derives a linear propagation equation of the primary reflection waves based on the relative impedance variation through high frequency approximation.Then,on the basis of the linear propagation equation,it derives the relative impedance variation imaging method and its formula by using the linear inversion theory.The relative impedance variation imaging results obtained by the proposed method are deficient in fidelity and resolution,owing to the limitation of the frequency band of the reflected seismic data and to the inherent limitations of the imaging methods,which are approximate solutions to the waveform linear inversion problem.However,the computational complexity is equivalent to that of reverse time migration.The result of the model tests on synthetic data showed the effectiveness of the proposed method.

pre-stack seismic reflection data,high frequency approximation,reflection wave equation,linear inversion,relative impedance variations,imaging

P631

：A

1000-1441(2017)05-0651-07DOI:10.3969/j.issn.1000-1441.2017.05.005

陈生昌,周华敏.基于反射波动方程的叠前地震反射数据波阻抗相对变化成像研究[J].石油物探,2017,56(5):657

CHEN Shengchang,ZHOU Huamin.A relative impedance variation imaging of prestack seismic reflection data based on reflection wave equation

[J].Geophysical Prospecting for Petroleum,2017,56(5):657

2016-10-11;改回日期：2017-04-06。

陈生昌(1965—),男,教授,博士生导师,主要从事勘探地球物理和计算地球物理研究。

国家自然科学基金项目(41074133,41374001)、国家科技重大专项(2016ZX05033002)共同资助。

This research is financially supported by the National Natural Science Foundation of China (Grant Nos. 41074133,41374001) and National Science and Technology Major Project of China (Grant No. 2016ZX05033002).