高速列车车体可靠性参数灵敏度分析方法对比研究
向鹏霖,卢耀辉,党林媛,冯振,曾京
(1.西南交通大学 机械工程学院,四川 成都 610031; 2.西南交通大学 牵引动力国家重点实验室,四川 成都 610031)*
高速列车车体可靠性参数灵敏度分析方法对比研究
向鹏霖1,卢耀辉1,党林媛1,冯振1,曾京2
(1.西南交通大学 机械工程学院,四川 成都 610031; 2.西南交通大学 牵引动力国家重点实验室,四川 成都 610031)*
以某型高速列车车体为研究对象,建立车体参数化有限元模型,将车体的材料属性、几何尺寸和载荷大小等参数设为随机变量,基于概率分析方法,通过统计分析得到其分布参数,分别基于蒙特卡洛和响应面数值模拟方法,求解车体的参数灵敏度.分析结果表明:在所选随机变量中,车体底架板材1、板材4和板材6的板厚尺寸对车体关注部位应力影响显著,设计过程中应对该变量进行严格控制;使用蒙特卡洛法和响应面法得到的灵敏度结果一致,其中响应面法缩减了求解时间;采用概率设计方法代替传统的定值设计方法,可以为高速列车车体的可靠性设计提供新的途径.
高速列车车体;参数灵敏度;可靠性;蒙特卡罗法;响应面法
0 引言
高速列车车体的强度可靠性受到多项变量的影响,在传统的车体强度设计中,这些变量采用确定性的数据,利用安全系数来评价其可靠性[1].当对可靠性的要求较高时,往往会造成结构的冗余[2- 3].因此,分析车体结构变量参数灵敏度,对车体进行参数优化成为了研究热点.随着研究的不断深入,一次二阶矩法迅速发展并广泛应用于实际工程设计中,已经成为结构可靠度分析计算的基本方法.张义民等[4- 6]利用神经网络法得到应力关于变量的显式表达式,分别对构架等的参数灵敏度进行了分析,对其可靠性参数优化提出了指导建议.蒙特卡洛法不用考虑功能函数的非线性和极限状态曲面的复杂性,回避了可靠性分析中的数学困难[7].卢耀辉[8]采用蒙特卡洛方法对构架参数灵敏度进行计算,为构架优化设计提供了参考.白迎春[9]对客车的中门梁的尺寸参数进行了灵敏度分析,为客车中门梁的结构优化
提供参考.虽然蒙特卡罗法具有直接解决问题的能力,但所需要的数值模拟数目通常很大,耗费计算资源且效率较低.响应面法通过拟合一个响应面来替代未知的真实状态曲面进行可靠度分析,则可以提高计算效率[10].梁明轩通过有限元仿真构建了轿车主减速齿轮最大接触应力完全二次响应面,研究了可靠度对参数的灵敏度,得到可靠度对压力角较为敏感的结果[11].目前,响应面方法还没有被广泛地使用在高速列车车体的参数灵敏度分析中.
为了确保高速列车车体具有高的运行安全可靠性,将概率理论和可靠性设计方法应用于高速列车车体的设计中,综合考虑列车服役过程中载荷随机性、车体铝合金材料性能随机性以及车体几何参数随机性,研究这些变量参数灵敏度,同时比较参数灵敏度计算方法,为车体的结构参数优化提供依据.
1 车体参数化有限元模型建立
本文以某型动车组头车为研究对象,针对其采用中空铝合金挤压型材薄板焊接的特点,采用shell63单元进行离散,网格尺寸设为50 mm,模型一共包括993 176个单元、871 559个节点,见图1.通过对车体空气弹簧安装位置进行约束,施加静态重力载荷,对车体进行静强度计算,车体当量应力分布如图2所示.选择车体强度薄弱的部位作为可靠度参数灵敏度计算的关注点,共6处,点1为车门上门角位置,点2、点3为二位端车窗窗角位置,点4为底架设备悬挂处,5为车门门柱底架连接部位,点6为一位端空气弹簧约束位置处.

图1 车体有限元模型
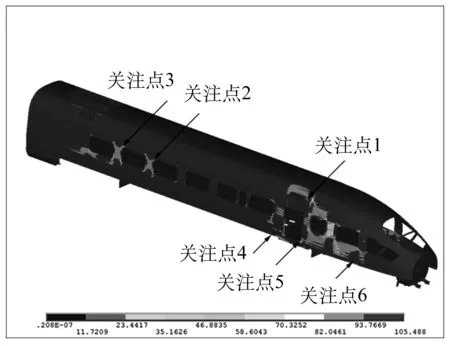
图2 车体当量应力分布及关注点位置示意图
根据确定的6个关注点位置,选择可能对这些位置的应力产生影响的变量进行灵敏度分析,选取的随机变量包括底架侧梁板厚、设备与空簧载荷及材料属性等.在有限元软件中将这些变量用变量名表示而非具体的数值,分别在单元的实
常数或者材料属性中采用这些参数的变量名,建立出参数化的车体有限元模型.通过软件中的概率设计模块(PDS)设定这些变量分布的均值和标准差,则这些变量的取值会在按照响应的分布进行随机抽样,最后输入到参数化的有限元模型中进行分析计算,获得响应特征的仿真结果,即可对车体结构不确定性问题进行量化描述.各变量分布参数确定方法如下:
(1)载荷分布参数确定:列车运行过程中,轮轨激励导致车体与转向架空气弹簧之间产生动态变化的作用载荷,确定四个空气弹簧载荷变化均服从正态分布并统计得到其分布参数;车体底架集中设备载荷考虑为随机载荷变量,设定其为正态分布,参照EN12663-1中给定的经验加速度确定变异系数为0.1;
(2)板厚分布参数确定:高速列车车体底架采用无中梁结构,侧梁为主要承载结构,几何尺寸的随机性主要考虑底架侧梁,侧梁横截面如图3所示,其板厚服从正态分布,分布参数由加工几何公差依据3σ原则,参考GB/T 14848-2008《铝及铝合金挤压型材尺寸偏差》来确定;
(3)材料性能分布参数确定:车体铝合金型材弹性模量均值为70 GPa,文献表明材料性能参数服从正态分布,确定其变异系数为0.03[12- 13].

图3 车体底架侧梁截面图
文中所考虑的车体载荷、几何尺寸及材料性能概率分布参数如表1所示,表中板材分布示意图见图3.

表1 车体随机变量分布类型及分布参数
2 车体结构参数灵敏度分析方法
2.1 结合有限元分析的蒙特卡洛方法
蒙特卡洛法(Monte Carlo)是一种以概率论和数理统计为理论基础的数值模拟方法,被广泛用来处理随机性问题.与有限元法相结合的蒙特卡洛法基于Spearman秩相关系数对参数灵敏度进行分析.Spearman秩相关系数检验方法是非参数统计中用来检验变量之间相关程度的重要方法.以求解结构响应应力σ对结构变量板厚t的灵敏度为例,介绍Spearman秩相关系数计算过程.对输入变量t进行n次随机抽样得到样本值t1,t2,…,tn,从而进行相应次数的有限元计算得到n次结构响应应力σ1,σ2,…,σn.记ti在t1,t2,…,tn中的秩为Ri,σi在σ1,σ2,…,σn中的秩为Qi,则上述数据对Spearman秩相关系数为:

Spearman秩相关系数取值范围为[-1,1],其绝对值越大,表明两变量的相关性越大,当两变量关系为单调递增时,相关系数为正,反之表明两变量呈单调递减关系.
采用拉丁超立方抽样方法对板厚、材料性能和载荷等输入变量进行随机抽样,由于模型计算量较大,抽样次数设置为1 000次.将抽样值调入参数化有限元模型进行确定性计算,记录6个关注部位应力响应参量值,基于Spearman秩求解参数灵敏度.
2.2 响应面函数方法
响应面法的基本思想是通过近似构造一个具有明确表达形式的多项式来表达隐式功能函数,本质上来说,响应面法是一套统计方法,用这种方法来寻找考虑了输入变量值的变异或不确定性之后的最佳响应值[14].利用有限元进行响应面灵敏度计算包括以下步骤:试验设计、样本计算、响应面拟合和参数修正.以结构的应力σ为因变量,xi(i=1,2,…,k)为k个设计参数,并假设以下关系成立:

根据表1中的参数分布进行分析,采用响应面进行残差计算,最终得到参数灵敏度G结果.
式中,p为设计参数,且VLB≤p≤VUB,VLB,VUB为设计参数的上、下限;{fE},{fA}分别为分析和试验的结果;G为灵敏度矩阵;Δp为设计参数的修改量.
在灵敏度计算中,响应面法考虑基本输入变量与蒙特卡洛法所考虑变量相同,参数化有限元模型也相同.基于有限元软件概率设计(PDS)模块,采用回归分析方法拟合车体关注部位的应力响应面函数.表2为经过步进回归分析滤掉不灵敏参数,略去极小的函数项系数(如β7,β8等)后得到的23个响应面函数项及其相关系数,各项函数项下标数字与表1中变量序号相对应,响应特征值等于23个函数项与其相关系数乘积的总和,见式(2).

表2 响应面函数参数计算结果
响应面拟合质量的优劣密切关系到参数灵敏度分析结果的准确性,所以需要对拟合得到的响应面函数进行评价.将采用响应面函数与有限元计算求得的车窗位置应力结果进行对比,得到最大相对误差为0.4%,这说明响应面函数较好地逼近了有限元结果,具有很高的精度.
3 两种方法灵敏度结果对比分析
3.1 基于蒙特卡洛方法的参数灵敏度结果
为方便对比载荷、板厚和材料性能对车体应力的影响,将随机输入变量对6个关注点应力的参数灵敏度因子列出,见表3,表中“—”表示该变量对应力影响不显著.将车门门角位置关注点1的灵敏度结果绘制为图4后可以看出,变流器载荷和一位端二系载荷对其应力影响最为显著,参数灵敏度因子分别为32.75%和18.73%,均为正相关;底架侧梁板材厚度对应力也有一定影响,其中板材1、板材4和板材6对其影响相对较大,随着板厚的增加,关注点1应力响应减小,为负相关.综合来看,底架侧梁板材对不同位置关注点影响不同,其中板材1、板材4和板材6对应力影响显著,在设计生产过程中对影响显著的板厚尺寸进行严格控制,对于影响不显著的板材尺寸可以在优化设计中减小冗余设计;二系空气弹簧载荷对车体应力影响显著,可通过调整车体悬挂参数减小轮轨冲击导致的垂向振动;同时车底悬挂设备对6个关注点应力均有显著影响,对悬挂设备质量及吊挂点的选择应加以控制.
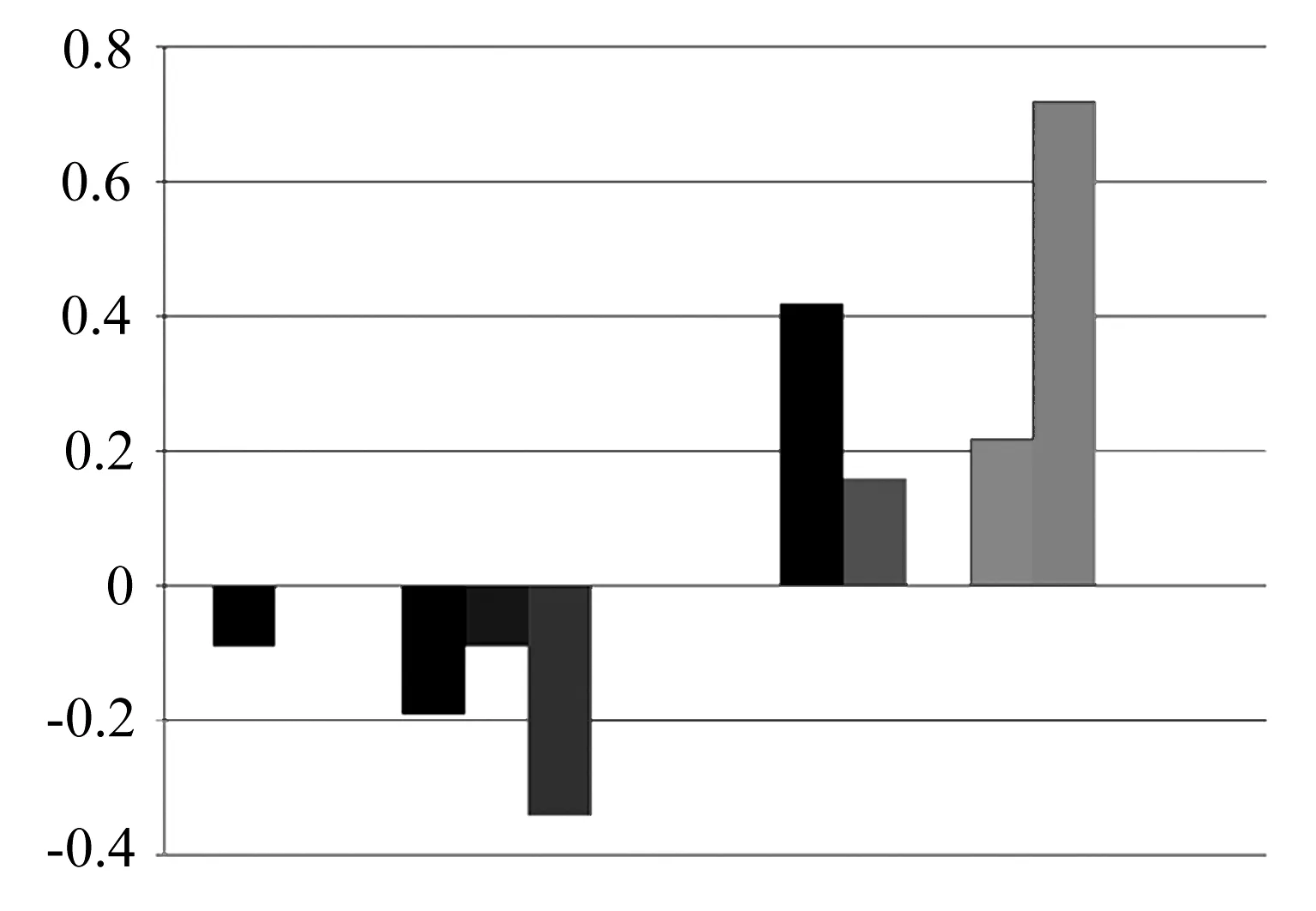

图4 关注点1应力的参数灵敏度及灵敏度因子图

表3 车体关注部位参数灵敏度因子表 %
3.2 基于响应面法的参数灵敏度结果
通过表2中的拟合系数建立响应面函数求解应力响应,进行10 000次模拟仿真,求解得到随机变量参数灵敏度结果,关注点1的灵敏度及灵敏度因子结果见图5.
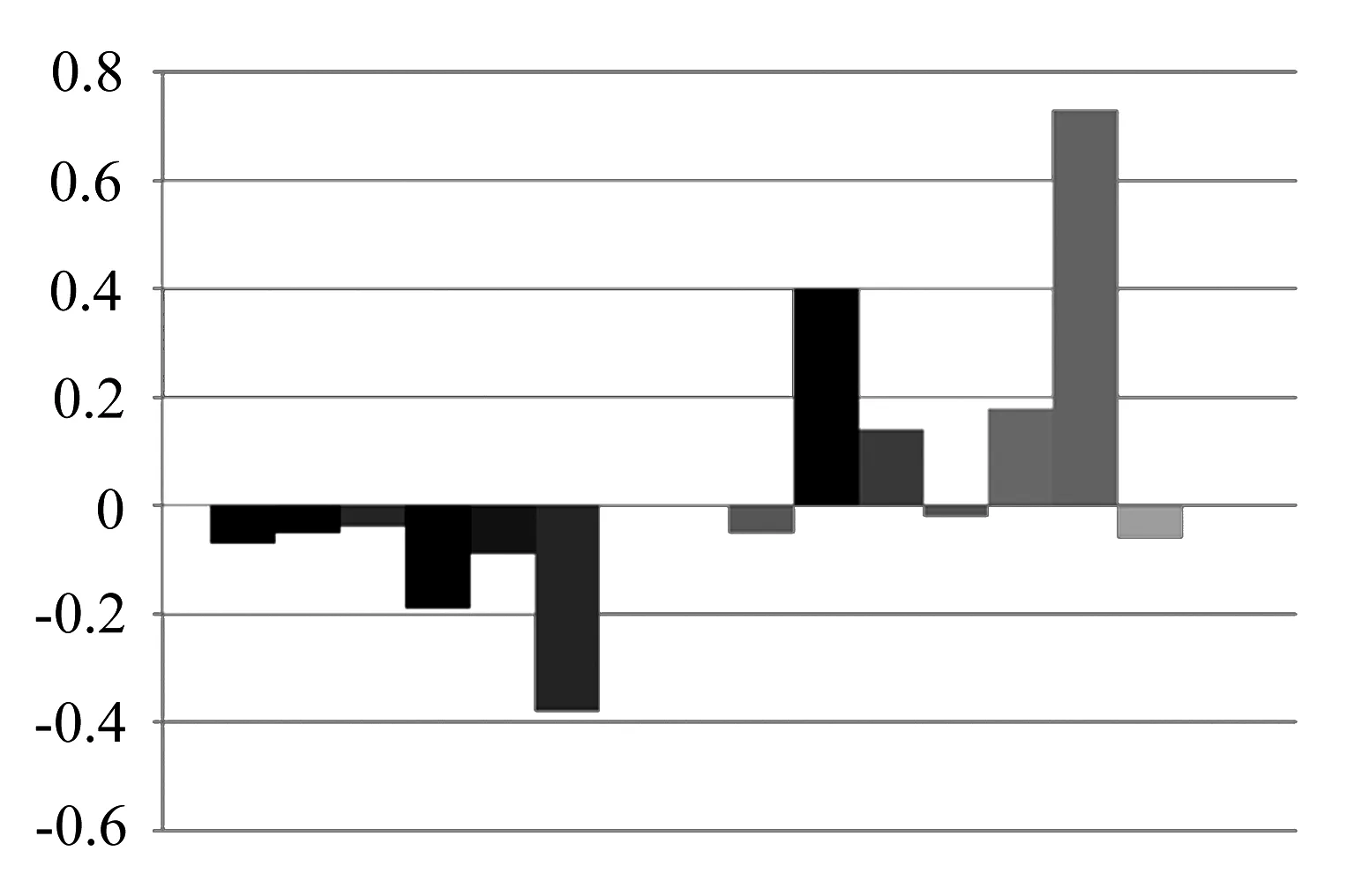
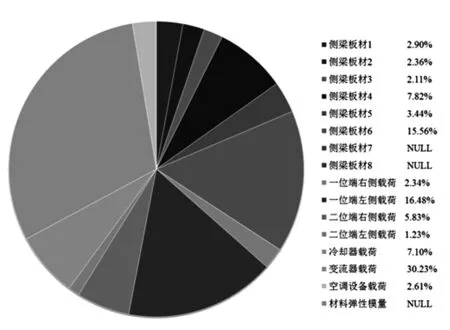
图5 关注点1应力的参数灵敏度及灵敏度因子图
同样将随机输入变量中对应6个关注点应力的参数灵敏度因子结果列出,见表4.可以看出,响应面法计算的灵敏度因子结果与表3中所示的结果差别不大,根据灵敏度因子结果所能够推测出的结构变量对可靠性的影响规律也基本一致,但可以发现在响应面法计算的关注点1的结果中,反映出了更多参数的灵敏度因子,如板材2、板材3、二位端左侧载荷、空调设备载荷等.

表4 车体关注部位参数灵敏度因子表 %
3.3 蒙特卡洛法与响应面法结果对比分析
采用同一个参数化有限元模型,确定响应面函数,针对表1随机输入变量进行10 000次模拟仿真,得到参数灵敏度结果与上文蒙特卡洛法得到结果一致.对于6个关注点位置的应力,响应面法得到影响最为显著的参量同样分别是变流器载荷、一位端左侧空簧处载荷、二位端右侧空簧处载荷、侧梁板材6板厚尺寸、侧梁板材4板厚尺寸和侧梁板材1板厚尺寸,并且求得最大的参量灵敏度因子结果相近,如图6所示.由于响应面法模拟次数远远多于蒙特卡洛法模拟次数,故响应面法结果中反映出更多对应力影响显著的参量.
蒙特卡洛法对随机变量抽样后代入有限元模型进行计算,针对本文车体模型完成一次有限元计算需要15 min,进行1 000次模拟计算花费大量的时间.而拟合得到响应面后,将随机输入变量抽样值代入函数进行数学运算,完成10 000次模拟仅仅需要几秒钟,可见大大减少了运算时间.但需要指出的是,增加响应面法仿真次数并不能提高其求解精度,因为其求解精度由所拟合响应面的准确程度而非循环仿真次数决定.
4 结论
针对某型高速列车车体,考虑车体几何尺寸、材料性能和载荷的随机性,确定这些随机变量的分布参数,建立车体概率有限元模型,分别采用蒙特卡洛数值模拟法和响应面数值模拟法对车体进行可靠性分析,求解车体强度参数灵敏度,并对两种数值模拟方法进行对比分析,得到以下主要结论:
(1)计算分析得到了对车体强度影响显著的参数,车体底架板材1、板材4和板材6的板厚尺寸对车体关注部位应力影响显著,设计生产过程中应对该变量进行严格控制,对于影响不显著的板材尺寸可以在优化设计中减小冗余设计;
(2)大型复杂结构的功能函数无法显式表达时,可采用与有限元相结合的数值计算方法求解其参数灵敏度,其中采用蒙特卡洛法和响应面法得到灵敏度结果基本一致,但响应面法可极大缩减求解时间,对多变量大型复杂结构采用响应面法求解其参数灵敏度较经济;
(3)高速列车车体的强度可靠性是关系其运行安全的最重要的保障,在高速列车车体设计中采用参数灵敏度分析的结果对车体进行优化设计显得非常重要.
[1]卢耀辉.铁道客车转向架焊接构架疲劳可靠性研究[D].成都:西南交通大学, 2011.
[2]REH S,BELEY J D,MUKHERJEE S,et al.Probabilistic finite element analysis using ANSYS [J].Structural Safety,2006,28:17- 43.
[3]周元,傅茂海,邵朋朋,等.基于ANSYS的快速货车转向架牵引拉杆可靠性分析[J].机械工程与自动化,2012,170(1):33- 35.
[4]张义民,朱丽莎,唐乐,等.刚柔混合非线性转子系统的动态应力可靠性及可靠性灵敏度研究[J].机械工程学报,2011,47(2):159- 165.
[5]王长一,张义民,张振先,等.某转向架构架的可靠性及可靠性灵敏度[J].东北大学学报(自然科学版),2012,33(5):711- 714.
[6]朱丽莎,张义民,卢昊,等.基于神经网络的转子振动可靠性灵敏度分析[J].计算机集成制造系统,2012,18(1):149- 155.
[7]穆志韬,邢玮,周立建.基于神经网络与蒙特卡洛方法的疲劳寿命可靠性分析[J].海军航空工程学院学报,2012,27(1):55- 60.
[8]卢耀辉,曾京,邬平波,等.铁道车辆转向架构架可靠性参数灵敏度分析[J].中国铁道科学,2010,31(1):111- 115.
[9]白迎春.基于灵敏度分析的客车结构优化设计[D].合肥:合肥工业大学,2009.
[10]吕大刚,贾明明,李刚.结构可靠度分析的均匀设计响应面法[J].工程力学,2011,28(7):109- 116.
[11]梁明轩,王晓林,袁惠群,等.基于响应面法的轿车主减速齿轮可靠性灵敏度研究[J].中国机械工程,2016,27(4):555- 559.
[12]郭小农,沈祖炎,李元齐,等.国产结构用铝合金材料本构关系及物理力学性能研究[J].建筑结构学报,2007,28(6):110- 117.
[13]牟致忠.机械可靠性—理论·方法·应用[M].北京:机械工业出版社,2011:84- 85.
[14]王永菲,王成国.响应面法的理论和应用[J].中央民族大学学报(自然科学版),2005,14(3):236- 240.
Method Comparison Research of Reliability Parametric Sensitivity Analysis for High Speed Train Carbody
XIANG Penglin1,LU Yaohui1,DANG Linyuan1,FENG Zhen1,ZENG Jing2
(1.School of Mechanical Engineering,Southwest Jiaotong University,Chengdu 610031,China; 2.Traction Power State Key Laboratory,Southwest Jiaotong University,Chengdu 610031,China)
A high speed train carbody was taken as the research subject,and its parametric finite element model was established with material attributes, geometric parameters and loads as the random variables.Based on probabilistic method,the distribution parameter values were obtained by using statistical analysis which is used in the calculation of parametric sensitivity of carbody by Monte Carlo method and response surface method respectively.The results show that in all chosen random variable parameters,the thickness of plates 1,4 and 6 in chassis show significant influence on the stress of concerned positions,which should be controlled strictly in design process.The sensitivity results calculated by Monte Carlo method and Response Surface method are basically consistent,but using the response surface method can greatly reduce the solution time.Using probability design method to replace the traditional fixed value design method could provide a new way for the reliability design of the high-speed train carbody.
high speed train carbody;parametric sensitivity;reliability;Monte Carlo method;response surface method
1673- 9590(2017)05- 0015- 07
A
2016- 12- 15
国家自然科学基金资助项目(51275428)
向鹏霖(1992-),男,硕士研究生; 卢耀辉(1973-),男,副教授,博士,主要从事车辆结构疲劳强度可靠性与动力学研究
E-mail:yhlu2000@suojut.edu.cn.

