弧面凸轮侧铣加工刀轨的空间线性回归分析

胡东方 郭建伟 任小中

1.河南科技大学机电工程学院,洛阳,4710032.机械装备先进制造河南省协同创新中心，洛阳,471003

弧面凸轮侧铣加工刀轨的空间线性回归分析

胡东方1,2郭建伟1,2任小中1,2

1.河南科技大学机电工程学院,洛阳,4710032.机械装备先进制造河南省协同创新中心，洛阳,471003

为减小弧面凸轮非等径加工存在的法矢异向误差，根据空间线性回归算法的NURBS直纹面生成原理，寻求加工误差最小的刀轴矢量，进行初步拟合。通过迭代逼近减小初始刀轴矢量误差，将刀轴作为NURBS直纹面母线来重构理论刀轴回归轨迹面。利用最小二乘法进行进一步优化，建立了弧面凸轮侧铣加工刀轨误差优化模型，提出了求解该优化模型的一种实数编码的人工免疫算法。以左旋弧面凸轮进行矢量数值计算和仿真，验证了该算法的有效性。

弧面凸轮；非等径侧铣；线性回归；NURBS直纹面

0 引言

由于凸轮机构具有结构紧凑、分度精度高、模态性能好等优势，高速精密凸轮机构被越来越多地应用在纺织、动力以及航空航天领域，因此对凸轮的制造工艺要求也越来越高。凸轮廓面的加工精度决定了其廓面的准确度，进而影响了机构分度和传动的精度。在传统的加工方式中，弧面凸轮的加工多采用范成法[1]加工，即通过刀具与工件之间类似滚子与凸轮的共轭运动，采用与滚子直径相同的刀具进行加工，再通过刀具补偿消除螺旋角和走刀转角误差即可加工出精度很高的弧面凸轮[2]，这种加工方式称为等径加工。该加工方式要求在精加工时刀具直径必须与滚子直径保持一致，但是在实际的加工中不可避免地会出现刀具磨损，从而因刀具半径减小造成工件加工误差。在生产滚子半径较大的凸轮时，制造和使用等径刀具加工成本较高，因此，可选择非等径刀具进行加工，即在侧铣加工中采用刀具半径小于滚子半径的加工方式，扩大了工艺范围，同时这也是实际生产加工弧面凸轮中经常用到的加工方式。

近年来，凸轮非等径侧铣加工刀轨优化问题引起了国内外广大学者的关注,研究重点放在两种加工方式上，即两重包络法加工[3]和刀位补偿法加工[4-5]。前者是一种点位加工方式，其廓面上的每一处有不同的刀位点，而重构过程中由于存在理论上的误差必然导致加工精度低，表面质量差；后者虽然刀位补偿的方向较为固定，但是在处理凸轮廓面时将其作为自由曲面处理，从而造成重构出的凸轮廓面存在较大的理论误差。孔马斌等[6]根据现有的弧面凸轮廓面加工工艺方法，提出刀轴轨迹面与凸轮廓面等距曲面的极差最小为优化目标的弧面凸轮单侧面数控加工刀位数据计算的优化算法；胡东方等[7]根据拟合误差敏感点的选择方法对理论加工刀轨曲面误差敏感点进行曲面重构，根据误差敏感点定义的等参数曲线来调整刀轨直纹面形状；葛荣雨等[8]根据NURBS曲面重构原理，利用最小二乘法从整体上提高理论加工精度；葛荣雨等[9]根据NURBS直纹面重构理论刀轴轨迹面，利用遗传算法对理论非等径刀轨曲面的刀位进行了优化。上述文献只考虑到刀具与工件的实时局部误差，没有考虑数控加工刀轨生成的要求，另外需要对理论刀轨面进行离散后再重构，所需初始数据量较大，采集过程繁琐，效率较低。

本文根据直纹面逼近的原理对NURBS拟合算法的应用进行研究，提出基于线性回归的NURBS直纹面重构的弧面凸轮侧铣加工刀轨优化算法，在减小加工误差生成的同时简化计算过程。

1 弧面凸轮数学模型分析

1.1弧面凸轮的理论表达式

利用微分几何建立三维坐标模型，针对弧面凸轮机构在实际啮合过程中滚子曲面与弧面凸轮廓面为共轭曲面的特点，建立弧面凸轮机构的几何模型如图1所示。 图中,o1x1y1z1为绝对坐标系，因为它与机架相连，所以也称固定坐标系；o2x2y2z2为弧面凸轮坐标系；o3x3y3z3为分度盘坐标系；orixriyrizri为滚子坐标系；ξ为滚子顶端到分度盘转轴的距离。

图1 弧面凸轮机构的数学模型Fig.1 The mathematical model of arc surface cam mechanism

按照空间包络曲面的共轭原理推导出弧面分度凸轮的廓面方程为

(1)

Γi=(i-1)×60°

(2)

式中，jCri为坐标系ojxjyjzj转换为坐标系oixiyizi的变换矩阵,i=1,2,3；γ2为凸轮转角；γ3为分度盘转角；L为分度盘与凸轮之间的距离，即z2轴与z3轴之间的距离；Γi为分度盘上滚子的角度关系；p为o3到滚子顶端的距离。

共轭曲面的曲面方程Fri在滚子坐标系orixriyrizri的矩阵表示为

(3)

式中，r为滚子半径；v、α为滚子与凸轮廓面啮合中的曲线坐标值;l为滚子长度。

弧面凸轮的滚子轴心轨迹面为不可展直纹面，弧面凸轮的工作廓面是滚子轴心轨迹面的等距曲面，根据式(2)和式(3)可得弧面凸轮在坐标系o2x2y2z2中的共轭曲面为

(4)

X2F=Lcosγ2-(ξ+v)cosγ2cos(γ3+Γi)+

rcosαcosγ2sin(γ3+Γi)+rsinαsinγ2

Y2F=-Lsinγ2+(ξ+v)sinγ2cos(γ3+Γi)-

rcosαsinγ2sin(γ3+Γi)+rsinαsinγ2

Z2F=-(ξ+v)sin(γ3+Γi)-rcosαcos(γ3+Γi)

根据直纹面等距曲面的性质，可得弧面凸轮的工作廓面为非直纹异型曲面,根据式(4)可推导出滚子轴心轨迹面的法矢方向n：

(5)

根据空间啮合原理可推导出啮合点处的法矢量方向的相对速度为零，则

(6)

将式(6)代入式(4)、式(5)中可求得凸轮与滚子的接触角θ为

(7)

根据直纹面的方程及等距面方程得到理论刀具轨迹曲面参数表达式：

S(ξ,γ)=Fri(ξ,γ)+rn(ξ,γ)

(8)

1.2非等径侧铣可加工性分析

侧铣加工刀位生成的本质是刀轨轴心作为直纹面母线生成侧铣加工曲面，而实际回转刀具侧刃与工件接触后生成所需曲面。对于弧面凸轮的侧铣加工，实际加工的刀具接触线是空间螺旋线。对于传统的误差控制方法就是通过测算刀轴始末点的刀具接触线和小尺寸刀具接触线之间距离来分析加工误差，最佳补偿半径就是Δr=R-r，即滚子半径r与刀具半径R之差。近年来对侧铣加工误差的控制主要是采用非等径刀轨曲面逼近的方法，该算法的思想是依靠重构曲面逼近理论非等径刀轨曲面，由式(7)知，接触角θ是关于分度盘与凸轮之间的距离L的非线性函数，所以任意给定一个凸轮转角γ2i，所对应的凸轮与滚子的理论接触线则发生变化，如图2所示。直线A为刀轴矢量的等径加工刀轴线，曲线B、曲线C为非等径加工刀轴曲线，并且直线A与曲线B、曲线C为凸轮与滚子的理论接触线上各点垂直滚子轴线的法矢方向的所有点集形成的曲线。

图2 非等径加工刀轴曲线Fig.2 Non equal diameter cutter shaft

对于等径加工的刀轴直线A可以实现凸轮廓面的重构即滚子半径等于刀具半径，进而可以得到弧面凸轮理论滚子轴线表达式：

(9)

而非等径加工刀轴理论曲面即为曲线B和曲线C扫掠生成的曲面。从本质上来分析，重构刀轨面逼近方法是一种基于自适应多点偏置约束算法，在优化侧铣加工算法过程中，从方向u和方向v划分网格采集数据点，可基于数据点进行曲面重构。

1.3理论刀轴轨迹面网格化离散分析

离散数据点的采样密集程度是由最终误差理论计算结果能否满足加工精度需求来决定的，并且提升加工精度方法之一即为增加数据点取样密度，而以往的文献中数据点采样方法通常为等距拓扑矩形阵列[10]，从本质上来说依然为固定方向上等弧长进行节点的划分。若采用拓扑矩形阵型对理论廓面进行划分，则这种划分方法并不能根据曲面实际曲率分布情况合理采集到能够反映曲面曲率分布的数据点。因此，需要一种算法来根据凸轮廓面曲面几何特性对数据点进行采集。数据点采集的过程在概率上可理解为一个抽样的过程，其抽样原则是采集的数据点分布应尽可能反映曲线和曲面的性质，最简单的思路就是在曲率变化较大的区域采用密集抽样，在相对平坦的区域采用稀疏抽样。

2 弧面凸轮侧铣加工刀轴矢量拟合

2.1基于线性回归的NURBS直纹面生成

回归问题的条件如下：

(1)收集的有效的数据；

(2)建立假设模型即一个函数，这个函数里含有未知的参数，通过学习，可以估计出参数。然后利用这个模型去预测/分类新的数据。

2.1.1型值点的初步确定

在加工过程中，回归函数u(x)未知，需要有效的实验数据去估计回归函数。在非等径侧铣加工中，要保证刀轴最优就需要保证加工误差最小，从式(9)中可以看出，非等径加工理论刀轴为空间曲线，空间曲线的曲率k和挠度τ的最值点是曲线形状变化最为剧烈的部分。因此可根据式(9)和下面公式得到采集数据点：

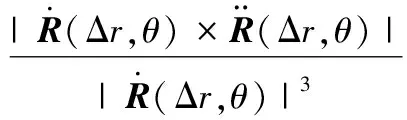
(10)

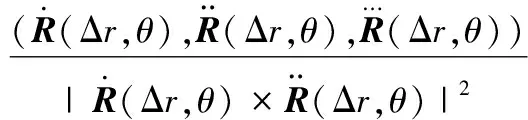
(11)

除了上述点外，曲线B的端点也能决定曲线的形状，因此也作为有效数据点，其值可在l∈[l0,l1]根据式(9)求得。

2.1.2空间型值点基于线性回归拟合模型

空间直线的方程可以化为

(12)

要求的参数是x0、y0、a、b(a、b均为正整数)。直线的方程可以化简成

(13)

写成矩阵形式为

(14)

当有b个点时第i个点的方程为

(15)

并联b个方程得到

(16)

刀轨直线拟合：

(17)

(18)

最终通过式(18)可求出回归模型解算的瞬时点刀轴的空间位置。

2.1.3线性回归的迭代优化

根据线性回归的性质可知，在线性回归中对参数m、n的解算是基于正交函数平方求极值的方法进行的，在概率问题解决过程中要求算法具有稳健性，即回归函数在求解中会出现异常值点，即个别变化较大的点[11],而正交函数平方求极值的方法对异常值点较为敏感。寻求刀轴的最优解过程即是找到空间中的某条直线段，使得非等径加工的理论刀轴曲线到该直线段的最大距离最小。因为在实际中所谓的“异常值点”均为刀轴上的有效点，因此可利用回归算法的敏感性，通过插入新的型值点来增加“异常值点”的个数，通过迭代对瞬时点刀轴的空间位置进行优化。

优化方法可通过以下过程进行：

(1)由式(18)初步拟合得到刀轴直线段l0；

(4)若满足则输出刀轴直线段，若不满足则采用等参数法增加新的型值点后，再次利用式(18)推导得到刀轴直线段lj，返回步骤(1)。

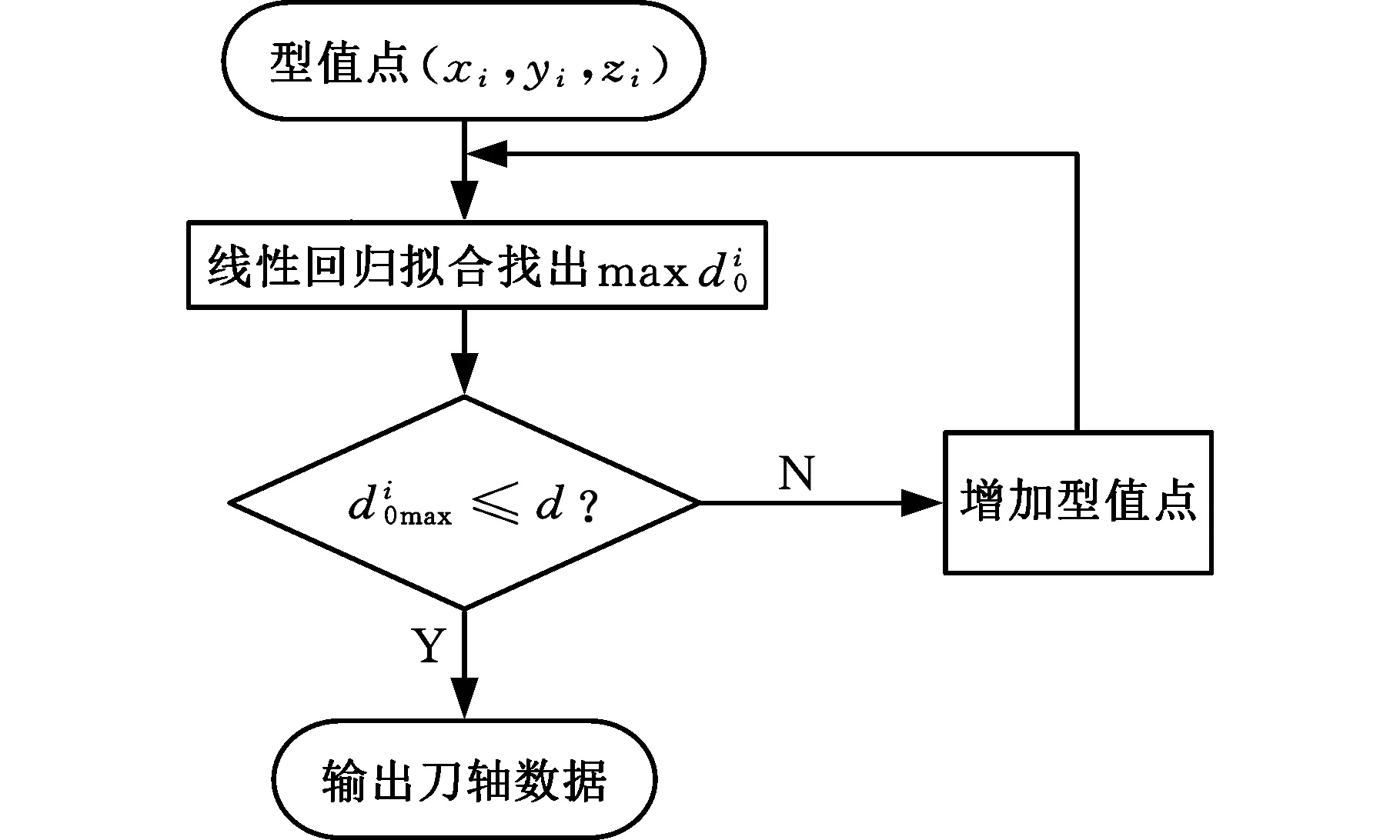
图3 线性回归算法流程图Fig.3 Flow chart of linear regression algorithm

2.1.4加工直纹面生成

由于理论刀轨面数据点之间权重相等，因此取NURBS曲面所有权因子w=1。CAM中常使用三次NURBS直纹面来表达曲线曲面，对于刀轨的非可展直纹面的重构这里也采用三次NURBS直纹面，因此令k=3。由微分几何，NURBS直纹面两条准线可表示为三次B-Spline形式[12]：

(19)

S(u,v)=(1-v)S1(u)+vS2(u)

(20)

u，v∈[0,1]

将式(19)代入式(20)中的NURBS直纹面方程得

(21)

2.1.5最小二乘优化法

由于上述算法的刀轴矢量是经过线性回归得到的，只是保证了单点刀位点的最优，因此利用蒙面插值法生成的直纹面还需优化才能作为刀轨轴迹面以达到整体误差最小。因为滚子轴迹面为直纹面[13]，故可以以逼近直纹面与滚子轴迹面的距离平方和为优化目标，建立最小二乘优化的目标函数：

(22)

2.2人工免疫算法的解算

人工免疫法是一种全局性概率搜索算法[14]，它基于自然选择和遗传变异等生物的遗传机制，其选择概率包括适应度和浓度信息，模拟了自然界生物免疫系统的功能。人工免疫算法将数学求解过程模拟为人或其他高等动物免疫系统的过程，通过复制、交叉、变异等算子进行遗传操作，产生优于父代的子代抗体，经逐代循环逼近最优解。

2.2.1抗体基因编码

人工免疫算法中的抗体由识别抗原的基因产生，抗体与抗原的特异性结合(即基因匹配程度)称之为亲和度[15]。由于基本的计算单元类似染色体的二进制字符串，故可以对优化后的数据点进行离散采集。考虑非等径侧铣加工刀位优化的求解属于多变量函数的求解问题，对于多个变量，采用二进制代码对每个变量的位置进行编排，然后根据信息熵来计算抗体和抗原之间的亲和度。

设抗体的容量为N，染色体的长度为M，等位基因的数目为S，采用二进制对抗体的基因进行编码，Ui={μ1,μ2,…,μn}，Ui∈Mi，Mi={m1,m2,…,mm},其中Mi为抗体总群，μi为等位基因，μi∈{0,1}，可得第i位的信息熵为

(23)

其中，ζ为基参数，ζ∈[2,N]，qij为等位基因在抗体中出现在第i位的概率，表达式为

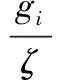
(24)

式中，gi为基因i上出现等位基因的总数。

抗体的平均信息熵为

(25)

2.2.2抗体与抗原的亲和度计算

根据抗原基因的二进制编码，定义抗原σ和抗原ω之间的亲和度ayσω：

(26)

式中，S(σ，ω)为抗原σ和抗体ω的结合强度。

在给定的抗体群中，任意给定的抗体ω的浓度为

(27)

式中，Ta和m分别为预先设定的阈值和常数。

2.3理论加工误差模型

侧铣加工的理论误差模型是通过刀轨曲面与滚子直纹面之间对应点之差的绝对值来测算的。由于理论刀轴轨迹面S(u,v)，其直纹面母线对应的即为刀具轴心线。逼近法理论加工误差为

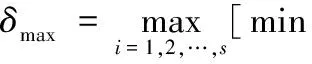
(28)

3 计算仿真与分析

现利用非等径刀具加工一个左旋弧面凸轮，如图4所示,已知从动件的半径为20 mm,长度为180 mm,转盘分度期的运动周期为正弦曲线，弧面凸轮分度周期为120°，72 mm≤ξ≤102 mm。

图4 弧面凸轮三维模型Fig.4 The 3D model of arc surface cam

根据式(8)得到了36条初始直纹面母线，通过采集数据点，通过线性回归算法优化得到三次NURBS直纹面的36×2个控制顶点，并根据式(21)和式(22)得出优化后的弧面凸轮的理论刀轨逼近直纹面,同时也生成了刀轨面，如图5和图6所示。

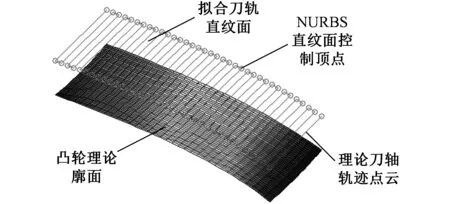
图5 理论刀轨型值点和刀轨直纹面Fig.5 The oretical cutter path value point and cutter rail ruled surface

图6 加工刀轴与理论刀轨面误差分布Fig.6 The error distribution of the cutter axis and the theoretical tool path

分别用不同半径的圆柱铣刀进行非等径侧铣加工，根据式(19)计算最大加工误差，并与刀位补偿法进行比较，结果如表1所示。

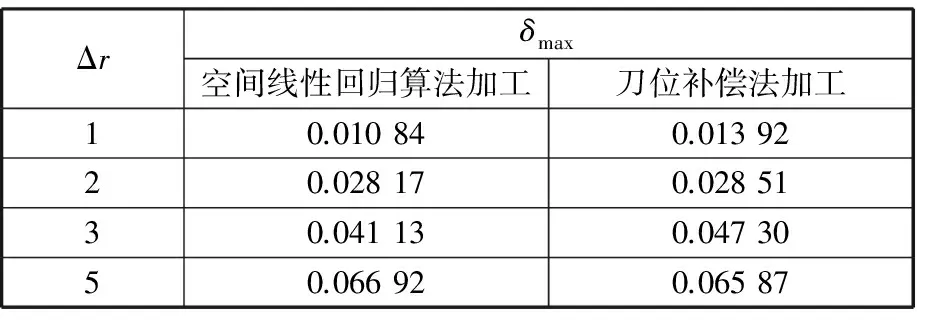
表1 最大加工误差比较

根据本文的空间线性回归算法和刀位补偿法拟合刀轨曲面的误差波动情况如图7所示。

图7 两种方法理论加工误差分布图Fig.6 The theoretical error distribution of two methods

通过表1和图7可以看出，在使用不同半径的立铣刀时，空间线性回归算法的拟合误差小于刀位补偿法拟合误差。相比刀位补偿法，空间线性回归算法在半径之差较小的区域内误差控制能力并不突出，但是在半径之差较大时，空间线性回归算法的误差控制能力优于刀位补偿法，这是因为该算法在此区域内曲率较大，获得的控制点较多，增加了该算法的控制能力。

4 结论

(1)弧面凸轮非等径加工存在法矢异向误差，且在瞬时刀位点上法向误差分布规律呈非可展直纹面。

(2)根据NURBS自身误差缺陷，分析了其误差变化趋势，并且在计算仿真数值验证中证明了当凸轮滚子半径与刀具之差较大时本文算法优于基于NURBS直纹面拟合的定量点的多点偏置算法。

(3)基于空间线性回归的非定量点的多点自由直纹面算法的刀位计算方法避免了繁琐的算法过程，并具有较高的理论加工精度，同时在一定程度上避免了以往NURBS算法缺陷，保证了刀位的连续性和光滑性，提高了实际的加工精度。

[1] YAN H S，CHEN H H. Geometry Design and Machining of Roller Gear Cams with Cylindrical Rollers[J]. Mechanism & Machine Theory，1994，29(6)：803-812.

[2] 牛兴华, 迟荣兰, 陈红, 等. 摆动从动件槽形圆柱凸轮的刀具轨迹及生成方法[J]. 农业机械学报, 2007, 38(1): 203-205. NIU Xinghua, CHI Ronglan, CHEN Hong, et al.Tool Path and Method for Forming Groove Shaped Cylindrical Cam with Oscillating Follower[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(1): 203-205.

[3] 邹惠君, 何有均, 郭为忠. 空间凸轮的两重包络法加工原理初探[J]. 机械传动, 1999, 23(4): 32-34. ZOU Huijun, HE Youjun, GUO Weizhong. Study on Machining Principle of Double Enveloping Method for Spatial Cam[J]. Journal of Mechanical Transmission, 1999, 23(4): 32-34.

[4] 尹明富. 弧面分度凸轮单侧面加工原理及刀位控制方法研究[J]. 中国机械工程， 2005， 16(2)： 127-130. YIN Mingfu， ZHAO Zhenhong. Study on One-side Machining Principle and Tool Path Control Method of the Globoidal Cam[J]. China Mechanical Engineering， 2005， 16(2)： 127-130.

[5] ZHANG Yitong, LU Ling, YIN Mingfu. Optimal Control Parinciple of Profile Errors for Machining of Cylinder CAM[J]. Chinese Journal of Mechanical Engineering, 1997, 10(3): 176-194.

[6] 孔马斌， 胡自化， 李慧， 等. 基于等距曲面的弧面凸轮单侧面数控加工刀位优化算法[J]. 机械工程学报， 2008， 44(11)： 277-282. KONG Mabin， HU Zihua， LI Hui， et al. New Cutter-location Optimization Algorithm and Error Analysis for Five-axis Flank Milling of Integral Impeller[J]. Journal of Mechanical Engineering， 2008， 44(11)： 276-282.

[7] 胡东方, 张文博. 基于NURBS直纹面拟合敏感点的空间凸轮侧铣刀轨算法优化[J]. 中国机械工程, 2016, 27(14): 1917-1924. HU Dongfang, ZHANG Wenbo. Flank Milling Cutter Path Optimization Method in Spatial Cam Machining Based on Reconstruction of NURBS Ruled Surface Driven by Sensitive Points[J]. China Mechanical Engineering， 2016, 27(14): 1917-1924.

[8] 葛荣雨， 冯显英， 宋现春， 等. 空间凸轮廓面侧铣加工及最小二乘优化刀位方法[J]. 中国机械工程， 2007， 18(15)： 1842-1845. GE Rongyu， FENG Xianying， SONG Xianchun， et al. Algorithm of Cutter Position for Side Milling of Spatial Cam Based on Least Square Optimization[J]. China Mechanical Engineering， 2007， 18(15)： 1842-1845.

[9] 葛荣雨， 冯显英， 宋现春， 等. 弧面凸轮非等径侧铣刀位计算与遗传算法优化[J]. 农业机械学报， 2007， 38(10)： 132-135. GE Rongyu， FENG Xianying， SONG Xianchun， et al. Calculation of Cutter Position for Unequal Diameter Milling of Globoidal Cam and Optimization Based on Genetic Algorithm[J]. Transactions of the Chinese Society for Agricultural Machinery， 2007， 38(10)： 132-135.

[10] 刘春明, 方漪. 寻找三维散乱数据点拓扑结构的一种算法[J]. 青岛大学学报(工程技术版), 2003, 18(3): 20-24. LIU Chunming, FANG Yi. An Algorithm of Searching Topological Structure from 3D Unorganized Points[J]. Journal of Qingdao University(Engineering & Technology Edition), 2007， 38(10)： 132-135.

[11] 冯守平, 石泽, 邹瑾，等. 一元线性回归模型中参数估计的几种方法比较[J]. 统计与决策, 2008, 24(12): 152-153. FENG Shouping, SHI Ze, ZOU Jin, et al. Comparison of Several Methods for Parameter Estimation in Linear Regression Model[J]. Statistics and Decision, 2008, 24(12): 152-153.

[12] 施法中. 计算机辅助几何设计及非均匀B样条曲线[M]. 北京： 高等教育出版社， 2013. SHI Fazhong. Computer Aided Geometric Design and Non-uniform B-spline Curve[M]. Beijing: High Education Press, 2013.

[13] 宫虎， 曹利新， 刘健， 等. 数控侧铣加工非可展直纹面的刀位整体优化原理与方法[J]. 机械工程学报， 2005， 41(11)： 134-139. GONG Hu， CAO Lixin， LIU Jian， et al. Global Optimization of Positioning Strategy for NC Flank Milling Undevelopable Ruled Surfaces[J]. Chinese Journal of Mechanical Engineering， 2005， 41(11)： 134-139.

[14] 李茂军, 罗安, 童调生. 人工免疫算法及其研究[J]. 控制理论及应用, 2004, 21(2): 153-157. LI Maojun, LUO An, TONG Tiaosheng. Artificial Immune Algorithm and Its Applications[J]. Control Theory & Applications, 2004, 21(2): 153-157.

[15] 刘韬. 人工免疫系统及其数据挖掘应用研究[M]. 徐州: 中国矿业大学出版社, 2010. LIU Tao. The Applications of Data Mining Technology in Artificial Immune System[M]. Xuzhou: China University of Mining and Technology Press, 2010.

(编辑郭伟)

LinearRegressionAnalysisofArcSurfaceCamSideMillingToolPaths

HU Dongfang1,2GUO Jianwei1,2REN Xiaozhong1,2
1.School of Mechatronics Engineering,Henan University of Science and Technology,Luoyang,Henan,471003 2.Collaborative Innovation Center of Machinery Equipment Advanced Manufacturing of Henan Province,Luoyang,Henan，471003

In order to reduce normal vector direction error exists for the arc surface cam unequal diameter machining method, according to the space linear regression algorithm NURBS (non-uniform rational B-Spline) ruled surface generation principles, a method was sought to minimize the machining errors of cutter axis vectors, and preliminary fitted. The initial cutter axis errors were reduced by iterative approximation, the cutter axis was taken as generatrix of NURBS ruled surface to restructure regression trajectory surface theoretical cutter axis. Using the least square method to further optimize, the optimization model of tool path errors for arc surface cam side milling was established, and a real coded artificial immune algorithm was proposed to solve the optimization model. The effectiveness of the proposed algorithm was verified by vector numerical calculations and simulations of the left-hand arc surface cams.

arc surface cam; unequal diameter side milling; linear regression; NURBS ruled surface

2017-02-16

国家自然科学基金资助项目(51575160)；河南省教育厅重大科技攻关项目(13A520232)；河南科技大学高级别项目培育基金资助项目(2011CX016)

TH132.47

10.3969/j.issn.1004-132X.2017.18.016

胡东方，男，1967年生。河南科技大学机电工程学院副教授。主要研究方向为虚拟产品设计与开发。出版专著1部，获河南省科技进步二等奖 1项、三等奖1项，发表论文30余篇。E-mail: hdf@haust.edu.cn。郭建伟，男，1991年生。河南科技大学机电工程学院硕士研究生。任小中，男，1957年生。河南科技大学机电工程学院教授。