平面四杆机构运动轨迹多目标综合优化及误差仿真研究*
王 琦,何 仁
(1.镇江高等专科学校 汽车工程学院,江苏 镇江 212003;2.江苏大学 汽车与交通工程学院,江苏 镇江 212013)
平面四杆机构运动轨迹多目标综合优化及误差仿真研究*
王 琦1,何 仁2
(1.镇江高等专科学校 汽车工程学院,江苏 镇江 212003;2.江苏大学 汽车与交通工程学院,江苏 镇江 212013)
针对平面四杆机构运动轨迹所产生的误差较大问题,引用改进差分进化算法对平面四杆机构运动轨迹误差进行优化。构造平面四杆机构运动简图,分析四杆机构变量参数。通过欧几里得距离误差函数推导出优化目标函数,采用改进差分进化算法对四杆机构约束条件进行多目标综合优化。结合具体实例,将优化后结果输入到Matlab软件进行误差仿真,并且与优化前误差仿真结果进行对比和分析。仿真结果表明:优化前,四杆机构运动轨迹所产生的横向和纵向误差峰值分别为0.25cm和0.19cm,优化后,四杆机构运动轨迹所产生的横向和纵向误差峰值分别为0.17cm和0.13cm,横向和纵向误差峰值分别降低了32.0%和31.6%。采用改进差分进化算法优化四杆机构运动轨迹,可以降低四杆机构运动轨迹产生的误差。
平面四杆机构;改进差分进化;运动轨迹;多目标优化
0 引言
随着机器向自动化方向的发展,连杆机构在机器中的作用越来越重要[1]。由于平面连杆机构连杆曲线具有多样性,所以可以实现各种复杂运动,特别是四杆机构和六杆机构应用非常广泛。平面连杆机构具有许多优点:①结构简单,加工容易,安装方便;②摩擦小,易于润滑,适合各种重载要求;③运动相对灵活,可以控制远距离危险物品的搬运等。平面连杆机构主要包括四杆机构、五杆机构、六杆机构及八杆机构等[2]。其中,四杆机构是其它连杆机构的重要组成部分。因此,四杆机构应用最为广泛,主要应用于缝纫机、搅拌机及起重机等。
目前,研究者从不同方向对四杆机构运动轨迹精度进行了研究。例如:文献[3]研究了平面四杆机构运动轨迹仿真问题,将四杆机构位置问题转换为空间坐标点,引用VB语言对运动轨迹进行编程,通过Matlab/Simulink软件进行仿真,VB语言程序较为复杂,四杆机构运动轨迹误差较大。文献[4-5]研究了四杆机构运动轨迹误差问题,确定四杆机构设计变量,采用了修正距离误差函数法构造目标函数,通过Matlab软件求解出最佳设计变量,并且对优化结果进行仿真,误差产生的峰值较大。文献[6-7]研究了轨迹生成四杆机构的遗传算法问题,创建平面四杆机构简图模型,构造平面轨迹点数学方程式,确定设计参数变量与目标函数表达式,采取遗传算法对四杆机构参数变量进行优化,优化结果容易陷入局部最优解,从而影响四杆机构运动轨迹的精度。针对以上问题,本文引入差分进化算法对四杆机构运动轨迹进行优化,并且对运动误差仿真和分析。建立平面四杆机构简图模型,通过欧几里得距离误差推导出优化目标函数,确定四杆机构优化参数变量。采用改进差分进化算法对平面四杆机构参数变量进行优化,得出四杆机构最优仿真参数。通过Matlab软件对四杆机构运动轨迹误差进行仿真验证,并且与优化前的误差仿真结果进行对比和分析。仿真结果显示出优化前与优化后的四杆机构运动轨迹误差曲线,为提高四杆机构运动的精度提供了参考。
1 平面四杆机构误差函数
1.1 坐标点方程式
平面四杆机构运动简图模型如图1所示。E表示连接点,φ1表示水平面与机架之间夹角,φ2表示输入角,l1表示机架长度,l2表示输入连杆长度,l3表示连接杆长度,l4表示输出连杆长度,l5和l6分别表示连接点E局部坐标长度。φ3表示连接杆l3与水平面之间夹角。x0和y0表示机架固定点O1的坐标。根据数学平面几何关系式可知,点E在平面坐标系中的方程式如下所示:
(1)

图1 四杆机构简图模型
1.2 运动参数设计
根据平面四杆机构运动的性质可知,平面四杆机构运动轨迹优化参数分别为x0、y0、l1、l2、l3、l4、l5、l6和φ1。同时,还需要优化输入角度φ2,将输入角度分成n个,然后对其进行优化。平面四杆机构优化参数的矢量关系式如下所示:
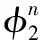
(2)
式中:n表示优化轨迹点的个数。
1.3 误差目标函数
欧几里得距离又名为欧式距离,在二维平面内,任意两点之间最短的距离就是欧几里得距离,计算公式[8]如下所示:
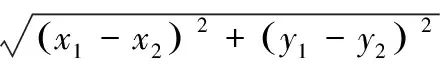
(3)
式中:d表示两点之间最短距离,(x1,y1)表示二维平面第一点坐标,(x2,y2)表示二维平面第二点坐标。
平面四杆机构运动轨迹误差函数是指理论轨迹与实际生成轨迹所构造的目标函数。以往研究大多采用欧几里得距离误差累积平方函数,如下所示:
(4)
式中:(xi,yi)表示四杆机构第i个理论轨迹点,(xi′,yi′)表示四杆机构第i个实际生成轨迹点,n表示四杆机构轨迹点个数。
因此,平面四杆机构运动轨迹位置平均误差目标函数计算式如下所示:
(5)
1.4 约束条件
平面四杆机构运动轨迹的约束条件必须满足以下3个部分:
(1)在四杆机构中,至少有一个连杆能够作整周旋转。因此,四杆机构的杆长应该满足曲柄摇杆机构整周运动的条件,即:
2[min(r1,r2,r3,r4)+max(r1,r2,r3,r4)]<
(r1+r2+r3+r4)
(6)
(3)四杆机构连杆长度必须为正值。
2 改进差分进化算法优化
2.1 多目标综合优化
多目标综合优化指的是在多个条件下搜索出最大值或者最小值。本文四杆机构目标函数误差是求最小值,其多目标综合优化数学表达式[9-10]如下所示:
miny=f(x)=[f1(x),f2(x),…,fn(x)]
(7)
s.t.gi(x)≤0,i=1,2,…,n
(8)
式中:x∈Rn表示n个未知设计变量,y∈Rn表示由变量组成的n个目标函数,gi(x)表示可行解区域内不等式约束条件。
2.2 差分进化算法
差分进化算法通常用来求解连续变量的全局最优问题,和其它算法类似,主要包括变异、交叉和选择三个部分[11]。改进差分进化算法主要是对变异和选择的改进,由帕累托搜索出的最优解和种群中产生变异的任意两个个体表达公式[12]如下:
(9)

2.3 变异改进
因为上一代是属于帕累托最优解集,算法的收敛速度较快,导致种群数量减少。所以,为了避免搜索过程中出现局部最优解,需要对其进行变异操作。在具体问题研究过程中,每个基因都会对目标函数产生影响也不同,有的基因对目标函数结果影响很大。因此,对基因的排列方式可以根据基因对目标函数的影响程度,影响程度越大,变异概率也就越大。本文研究的平面四杆机构,l5和l6的值对运动轨迹影响最大,那么变异概率就是最大。对此,本文把基因划分为4组进行变异操作[13],如下所示:
x←x+range×(2×U(0,1)-1)
(10)
(11)
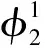
2.4 选择改进
差分进化算法的性能会受到选择操作的影响,选择操作不仅会影响差分进化算法收敛速度和多样性,而且还会影响到全局寻优能力。由平面四杆机构的约束条件(1)、(2)和(3)可以得出,改进后的选择操作如下所示:
(12)
(13)
(3)二者都不符合约束条件1,ga(Xi)最小的遗传给下一代,即:
(14)
(4)二者都符合约束条件1,起到支配作用的个体遗传给下一代。若二者无法进行比较,则目标函数和最小的遗传给下一代,即:
(15)
3 误差仿真与分析
平面四杆机构轨运动迹点选择11个指定点,借助于Matlab软件对改进差分进化算法优化尺寸进行计算,计算过程中需要的参数如下:种群最大迭代次数为500,种群数量为200,缩放因子为0.7,交叉概率为0.95,变异概率为0.85,变异操作过程中,a=0.35,b=0.65,c=0.85,选择操作过程中,n=400,则平面四杆机构优化前与优化后的参数对比结果如表1所示。
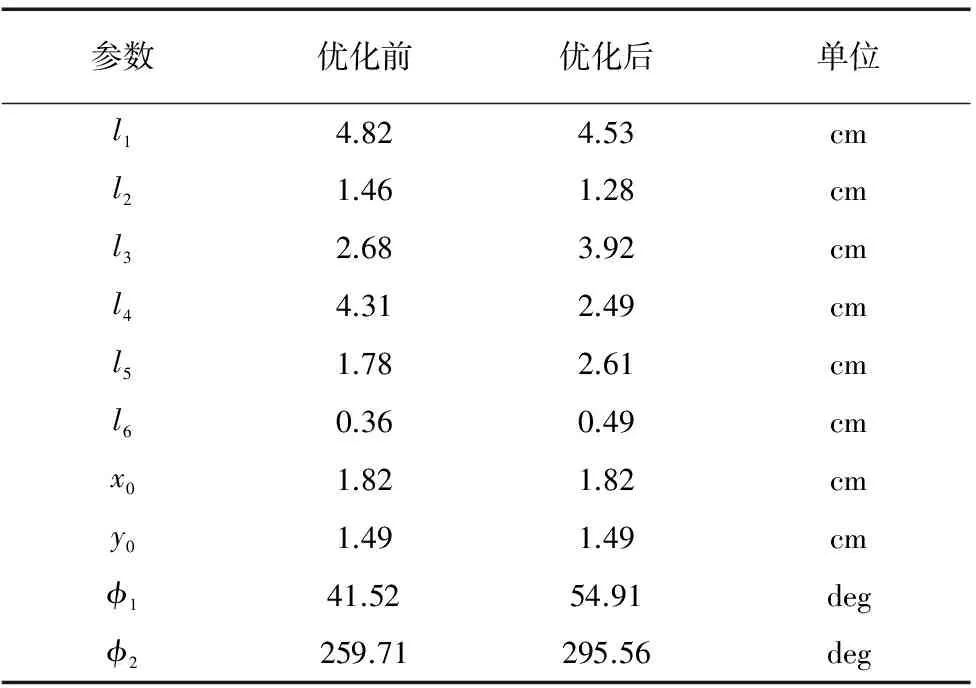
表1四杆机构优化参数
优化后的平面四杆机构及运动轨迹如图2所示。

图2 优化后四杆机构及运动轨迹
采用Matlab软件对优化后的平面四杆机构运动轨迹进行误差仿真。同时,与优化前的运动轨迹误差仿真结果进行对比。平面四杆机构横向运动轨迹误差仿真结果如图3所示,平面四杆机构纵向运动轨迹误差仿真结果如图4所示。
由图3仿真结果可知,优化前平面四杆机构运动轨迹横向误差产生的峰值为0.25cm,优化后平面四杆机构运动轨迹横向误差产生的峰值为0.17cm,横向误差大约降低了32.0%。由图4仿真结果可知,优化前平面四杆机构运动轨迹纵向误差产生的峰值为0.19cm,优化后平面四杆机构运动轨迹纵向误差产生的峰值为0.13cm,纵向误差大约降低了31.6%。因此,采用改进差分进化算法优化平面四杆机构,运动轨迹产生的误差相对较小,提高了平面四杆机构运动轨迹精度。
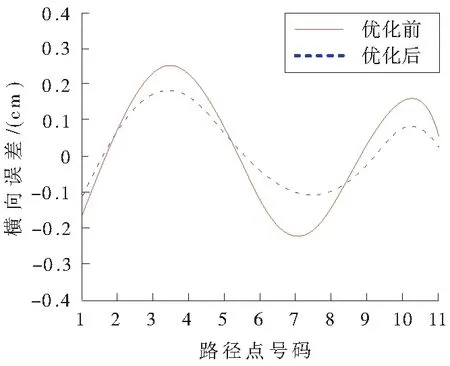
图3 运动轨迹横向误差仿真结果

图4 运动轨迹纵向误差仿真结果
4 结束语
本文研究了平面四杆机构运动轨迹误差问题,采用改进差分进化算法对四杆机构运动尺寸进行了优化。创建了平面四杆机构简图模型,设置了优化参数变量,推导了优化目标函数,添加了四杆机构运动约束条件。采取改进差分进化算法,将优化参数变量划分为4组,通过遗传迭代,得出最优仿真参数。采用Matlab软件对平面四杆机构横向和纵向运动轨迹误差进行仿真。同时,优化前仿真结果进行对比和分析。仿真结果表明,采用改进差分进化算法优化后的平面四杆机构横向和纵向运动轨迹误差峰值降低,为平面四杆机构运动轨迹深入的研究提供了参考依据。
[1] 赵彦微.平面四杆机构轨迹综合方法及可视化表达[D].哈尔滨:哈尔滨工业大学,2014.
[2] 张云娇.基于并联原理的机构运动学分析[D].天津:天津大学,2013.
[3] 贺兵,吴吉平,符浩,等.基于变速原动件的四杆机构轨迹和速度双目标优化综合[J].机械传动,2016,40(3):78-81.
[4] 魏静.采用Matlab和误差函数法对轨迹生成四杆机构的优化及仿真研究[J].机械与电子,2016,34(1):11-14.
[5] M Shariati. Optimal synthesis of function generator of four-bar linkages based on distribution of precision points [J].Meccanica,2011, 46(5):1007-1021.
[6] 张国平.食品机械平面四杆机构的遗传算法优化设计[J].食品机械,2010,26(3):117-119.
[7] 郭威,王水生,李华.基于实数编码遗传算法的轨迹综合优化设计[J].沈阳航空工业学院学报,2010,27(3): 68-69.
[8] 杨 帆.轨迹生成四杆机构优化及仿真研究[J].组合机床与自动化加工技术,2016, (10):36-39.
[9] 汪从哲,方跃法.基于差分进化算法的平面四杆机构轨迹和速度双目标优化综合[J].北京交通大学学报,2011,35(6):73-77.
[10] Jacek Bus′kiewicz. A method for optimal path synthesis of four-link planar mechanisms[J].Inverse Problems in Science and Engineering,2015,23(5):818-834.
[11] 乔英,高岳林,江巧永.一种新局部搜索策略的差分进化算法[J].太原理工大学学报,2011,42(4):349-351.
[12] 车林仙.面向机构分析与设计的差分进化算法研究[D].徐州:中国矿业大学,2012.
[13] P S Shiakolas,D Koladiya,J Kebrle.On the optimum synth-esis of four-bar linkages using differential evolution and the geometric centroid of precision positions[J].Inverse Problems in Engng,2012,10(6):485-500.
(编辑李秀敏)
ResearchonMulti-objectiveSyntheticOptimizationandErrorSimulationofMotionTrajectoryofPlanarFour-barLinkage
WANG Qi1,HE Ren2
(1.Department of Automotive Engineering, Zhenjiang College, Jiangsu Zhenjiang 212003,China; 2.School of Automobile and Traffic Engineering,Jiangsu University,Zhenjiang Jiangsu 212013,China)
Aiming at the large error of the motion of the planar four-bar mechanism,an improved differential evolution algorithm is used to optimize the trajectory error of planar four-bar mechanism. Structure four-bar mechanism,and analyze the variable parameters of four-bar mechanism.By using Euclidean distance error function,the optimal objective function is deduced,and an improved differential evolution algorithm is used to optimize the constraints of the four-bar linkage mechanism.The optimized results are input to the Matlab software for error simulation, and compared with the pre-optimization error simulation results. The simulation results show that the transverse and longitudinal error peaks of the four-bar mechanism are 0.25cm and 0.19cm respectively, and the peak of the transverse and longitudinal errors are 0.17cm and 0.13cm,and the horizontal and vertical error peak values decreased by 32.0% and 31.6% respectively.Using the improved differential evolution algorithm to optimize the trajectory of the four - bar mechanism, the error generated by the trajectory of the four - bar mechanism can be reduced.
Planar four-bar mechanism;Improved differential evolution;trajectory;multi-objective optimization
TH122;TG65
:A
1001-2265(2017)09-0055-04
10.13462/j.cnki.mmtamt.2017.09.014
2016-11-21;
:2016-12-17
国家自然科学基金项目(51275212);江苏省高等职业院校教师国内高级访问学者计划资助项目(2015FX098)
王琦(1976—),女,江苏东台人,镇江高等专科学校副教授,硕士,研究方向为机械自动化,(E-mail)qwang201611@163.com;何仁(1962—),男,南京人,江苏大学教授,博士生导师,研究方向为汽车机电一体化。

