5-DOF仿人型机械臂关节空间轨迹规划研究*

张 程，张 卓

(1.吉林大学 珠海学院，广东 珠海 519041;2.广东科学技术职业学院，广东 珠海 519041)

5-DOF仿人型机械臂关节空间轨迹规划研究*

张 程1，张 卓2

(1.吉林大学 珠海学院，广东 珠海 519041;2.广东科学技术职业学院，广东 珠海 519041)

文章以5-DOF仿人型机械臂为研究对象，讨论了工业机器人轨迹规划方法及相关问题。对该机械臂进行了运动学分析，建立了机械臂运动学方程，并针对典型搬运作业方式，以距离最优为目标选取空间梯形路径关键点，设计了基于关节空间五项多项式插值算法的轨迹规划方法，利用Robotics Toolbox工具箱进行机械臂虚拟建模及关节空间轨迹规划仿真。经验证，相对于传统矩形路径作业方式，该方法可以更好完成工业机器人搬运作业的轨迹规划问题，对进一步结合工艺参数研究工业机器人控制系统具有必要的理论及实践意义。

仿人型机械臂；轨迹规划；关节空间

0 引言

工业机器人是迄今为止机器人技术最重要的商业应用。工业机器人在执行某项操作任务时，会依据工艺参数附加某些实时的约束条件，如轨迹参数、运动位置、速度及加速度等，这些参数的确定即是轨迹规划的问题[1-2]。运动轨迹规划的优劣将直接影响机器人作业的质量。随着国内外学者在运动轨迹规划领域(如，机器学习、相似性运动及运动解析算法等)研究的不断深入，运动轨迹规划已经成为机器人研究领域的重要课题之一[3-5]。本文针对机器人运动轨迹规划的问题，以5-DOF仿人型机械臂为研究对象，利用分段轨迹规划的方法针对典型搬运作业进行轨迹规划研究，设计了一种5-DOF机械臂运动轨迹规划方法。该方法依据搬运作业任务设计梯形路径关键节点，采用关节空间法计算出预期的运动轨迹，使得机械臂可沿规划轨迹稳定、平滑且快速地到达位置，且能够移植到其它型号的串联机器人之中，具有良好的科研意义。

1 机械臂运动学模型

1.1 机械结构

仿人型机械臂也称为关节型机械臂，是由一系列通过关节相连的连杆组成的一个运动链[6]。关节通常分为旋转和平移两种，在机械臂和末端执行器之间的运动链中的关节称为手腕，机械臂和手腕组件主要用于定位末端执行器(以及其携带的工具)完成作业操作。图1展示了本文所研究的5-DOF仿人型机械臂的机械结构，其依据人类手臂的特征而设计，包括肩部、肘部和腕部。可以完成肩部旋转、大臂俯仰、肘部俯仰、小臂俯仰及腕部旋转的人体上肢运动，并配有末端执行器——夹持器，完成抓放、夹取等人体手部运动。该仿人型机械臂可以用于完成如搬运、码垛、喷漆及弧焊等作业。

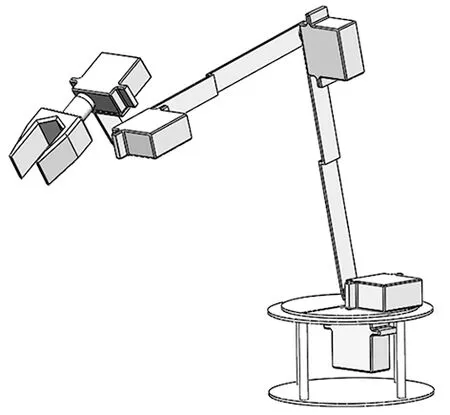
图1 5-DOF仿人型机械臂机械结构

1.2 运动学正解模型

(1)D-H参数确定

根据Denavit-Hartenberg参数法定义连杆坐标系。设x0y0z0为基座坐标系，其原点位于z0和z1的交点；z2平行于z3及z4；z4垂直于z5。xiyizi与机械臂第i个杆件固连，坐标原点在第i+1个关节的中心点处，选择xi轴与相应连杆的方向一致且处于(x0,y0)平面上，杆件长度αi-1为沿xi轴从zi-1到zi的距离；扭转角αi-1为绕xi-1从zi-1到zi旋转的角度；偏移距di为沿zi从xi-1到xi距离；关节角θi为绕zi从xi-1到xi旋转的角度[2,6]。由此确定5-DOF机械臂连杆坐标系如图2所示，连杆参数与关节变量的D-H参数表见表1。

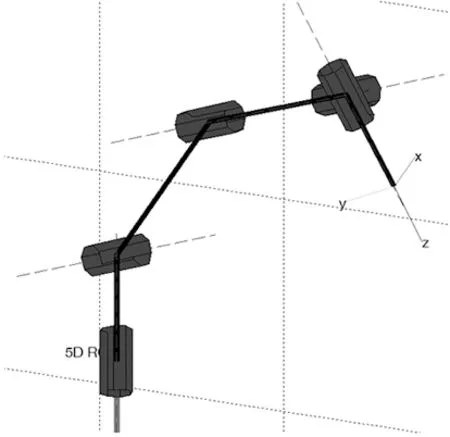
图2 机械臂连杆坐标系

表1 机械臂D-H参数与关节变量表

(2)变换矩阵计算

(1)

(2)

(3)

(4)

(5)

将各连杆变换矩阵相乘，即可得到机械臂的运动学方程：

(6)

式(6)为关节变量θ1，θ2，……，θ5的函数。该方程描述了末端执行器位置坐标与各关节转角关系，即机械手坐标系n的位置和方向相对基坐标系的坐标变换矩阵。至此，机械臂的运动学模型建立完毕。

2 关节空间轨迹插补算法

工业机器人轨迹规划可以在两种空间中进行：关节空间和操作空间。对于在奇异位形邻域内和存在冗余自由度情形的运动，操作空间轨迹规划可能面临难于求解的问题[7]。在此情形下，例如抓放作业和搬运作业的机器人比较适合于在关节空间进行规划，本文选择关节空间法进行轨迹规划。

2.1 运动学逆解

由上文所建立的运动方程，当已知机械臂末端执行器相对于基座标系的位姿矩阵T时，求解方程即可求出机械手的各个关节角度，此为运动学逆解[7]。关节空间规划轨迹，即使用关节角度的平滑插值函数θ(t)表达机器人的运行轨迹，得到一组满足轨迹约束条件的关节变量时间序列。

2.2 关节轨迹多项式插值算法

在轨迹规划之前，需设定约束条件。以机械臂的搬运作业为例，当抓取并移动释放物体时，要知道机械臂末端执行器在移动中的每个节点(起始点、上升点、下降点和目标点)的位姿、速度以及加速度的要求，且其极值不能超出每个关节变量可以移动的范围[6]。在满足上述条件的情况下，利用平滑插值函数θ(t)产生不同的轨迹曲线。假设起始点时刻的起始关节角度为θ0，经过运动学逆解能够获得终止点时刻tf的终止关节角度为θf。该轨迹函数θ(t)需要满足五个关节角度、角速度和角加速度在起始点和终止点的约束条件。其中，各关节角度在起始点和终止点的约束条件为式(7)：

(7)

各关节角速度在起始点和终止点的约束条件为式(8)：

(8)

各关节角加速度在起始点和终止点的约束条件为式(9)：

(9)

在上述各关节边界约束条件下，可以确定一个五阶多项式：

θ(t)=k0+k1t+k2t2+k3t3+K4t4+k5t5

(10)

其中，多项式(10)的系数k1，k2，……，k5必须满足上述各关节约束条件：

(11)

该线性方程组含有6个未知数和6个方程，其解为：

(12)

由此得到在约束条件下，对于初速度及终速度为零的关节运动的五次多项式插值函数为θ(t)，该插值函数表达了从起始点关节角度到终止点关节角度θf的变化。至此，完成了5阶多项式插值轨迹规划。

3 机械臂关节空间轨迹规划仿真

基于上述5-DOF机械臂的运动学模型，利用Robotics Toolbox工具箱进行关节空间插补算法的运动轨迹仿真[8-10]。首先根据本文中5-DOF机械臂的D-H参数，建立相应的机械臂对象模型5D-ROBT，如图3所示。

>>L{1} = link([alpha(1) a(1) theta(1) d(1)],'standard');

>>L{2} = link([alpha(2) a(2) theta(2) d(2)],'standard');

……

>>ROBT = robot(L,'ROBT');

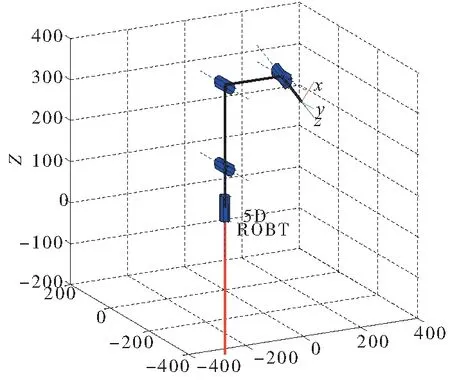
图3 机械臂Robotics Toolbox模型5D-ROBT

以机械臂的搬运作业为研究对象，预先对轨迹途径的关键点进行选定，将较复杂的运动路径分解成在关键点间的分段运动。在整个搬运任务实现过程中，在工作单元内设定5个工作点(机械臂预备点、物料初始点、抬手点、落手点和物料目地点)分别为Q0、Q1、Q2、Q3和Q4。机器人末端执行器从初始位置Q0出发，经规划路径到达Q1，抓取物块后经规划路径顺次经过Q2和Q3完成抬手、平移及落手动作，到达终点Q4并释放物料，最终完成对物料的搬运。给定末端执行器初始位置及依次到达的位姿矩阵如下：

>>Q0= [0 -1.57 1.57 -0.79 0];

>>Q1= [0 -0.95 1.67 -1.00 0];

>>Q2= [-0.21 -1.25 1.87 -1.00 0.79];

>>Q3= [-1.36 -1.25 1.87 -1.00 0];

>>Q4= [-1.57 -0.95 1.67 -1.00 0];

该分段轨迹规划方法与传统分段轨迹规划方法有所不同：传统分段轨迹规划方法抬手点处于物料原点空间位置的正上方，同时，落手点也处于物料目的点空间位置的正上方，运动轨迹为矩形轨迹，如图4所示，这样做是为了增加正确拾取的几率，但牺牲了时间。本文抬手点和落手点的空间位置是其投影在物料原点与物料目的点空间连线上的一点，即在物料抬起与落下的同时，在水平位置上还存在一段位移，运动轨迹为梯形轨迹。这种轨迹规划方法可以使物料从原点到目的点所经过的空间距离在一定程度上缩短，即距离最优。值得一提的是，若需多次往返的搬运动作，则可通过搬运策略的优化即可极大地缩短搬运时间，更好地提高工作效率及正确率。

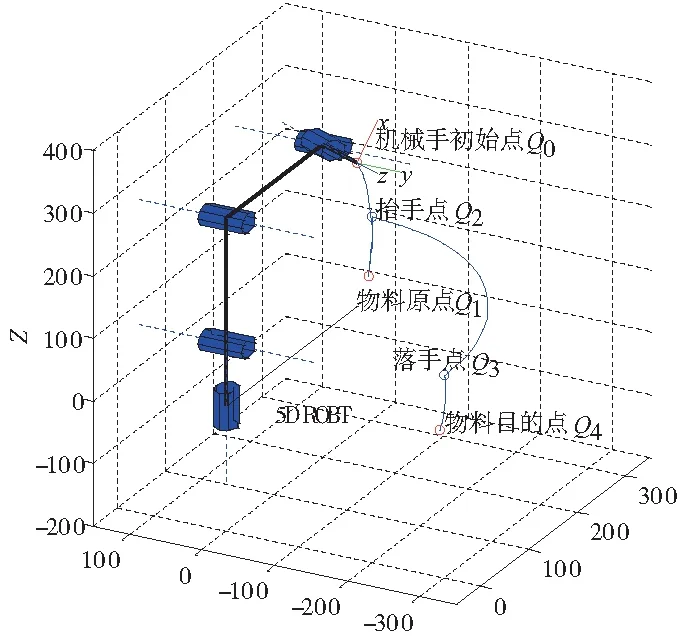
图4 传统分段轨迹规划路径

利用Robotics Toolbox工具箱进行逆运动学求解，得到各关节运动学变量。其计算结果是有关各个路径段的一组数据，在仿真图中对机械臂各关节的运动情况进行观察，根据关节空间内变量变化情况对末端执行器轨迹合理性进行验证，得到搬运作业过程及机械臂末端执行器轨迹路径如图5和图6所示。

>>plot(ROBT,theta)

>>hold on;hidden off;plot3(x,y,z)

>>hold on;hidden off;

>>plot3(T00(1,4),T00(2,4),T00(3,4),′ro′,′linewidth′,5)

……

>>plot3(T34(i,4,length(t)),T34(i+1,4,length(t)),T34(i+2,4,length(t)),′ro′,′linewidth′,5)

图5 搬运作业轨迹规划(起始点)

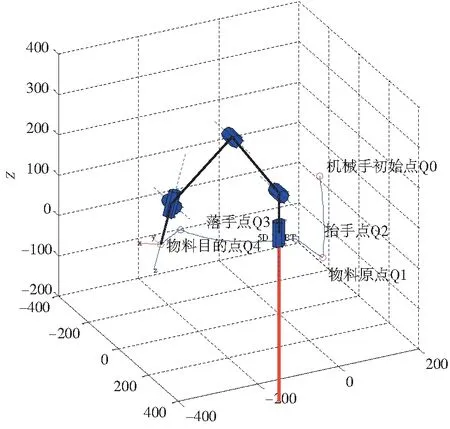
图6 搬运作业轨迹规划(终止点)

经算法仿真得到各关节角位移、角速度及角加速度数值对比曲线分别见图7、图8及图 9，图中实线为梯形规划参数曲线，虚线为矩形规划参数曲线。

>>plot(T,[Q01(:,i);Q12(:,i);Q23(:,i);Q34(:,i)])

>>plot(T,[QD01(:,i);QD12(:,i);QD23(:,i);QD34(:,i)])

>>plot(T,[QDD01(:,i);QDD12(:,i);QDD23(:,i);QDD34(:,i)])

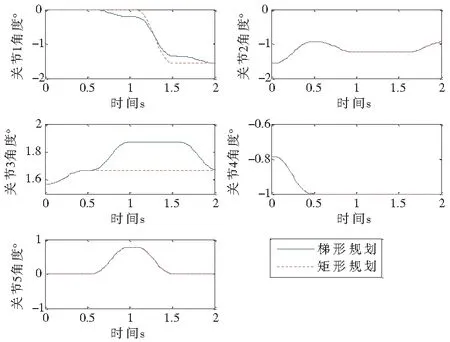
图7 各关节角位移随时间变化曲线对比

图8 各关节角速度随时间变化曲线对比

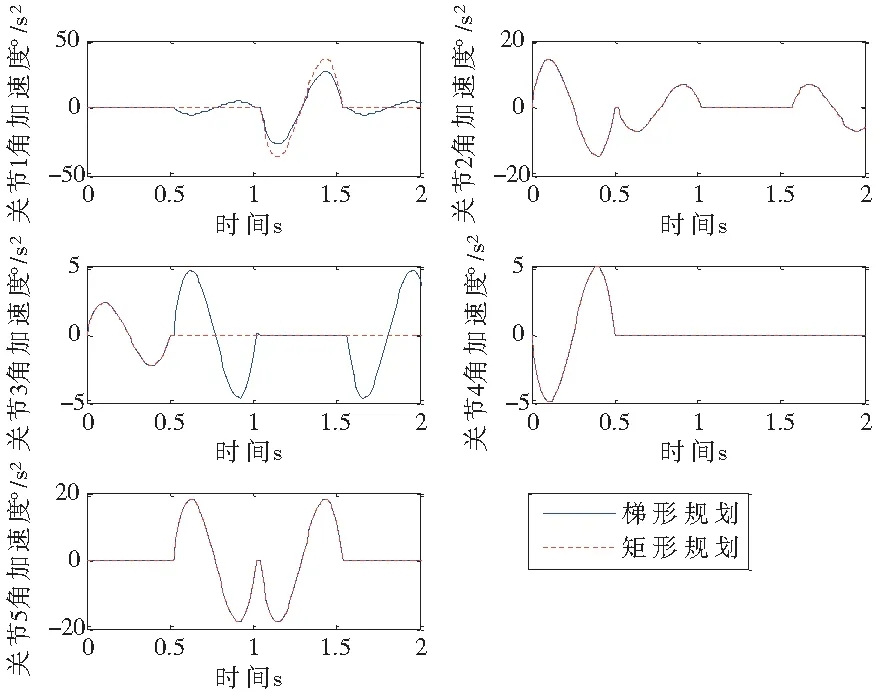
图9 各关节角加速度随时间变化曲线对比

根据图示对5个关节角运动学参数进行分析，可见本文方法从整体上改善了各关节轨迹运动参数。如关节1的角速度最大值减少了1.6°/s，角加速度最大值减少了10°/s2，使得角速度变化幅度较小，运动参数明显趋于平稳，运动曲线较平滑；与此同时，关节3角速度最大值增加了0.37°/s，角加速度最大值增加了2.3°/s2，该变化中机械臂关节角始终保持处于安全范围以内，且增幅较小，相对于关节1的明显改善，关节3的参数调整是完全符合作业运动要求的。据此可得本文所规划运动轨迹在整个运动过程中平稳光滑且速度较快，相对于传统矩形运动轨迹可以更好地满足搬运作业的实际需求。

4 结 论

本文以5-DOF仿人型机械臂为研究对象，设计了基于关节空间五次多项式的插补算法，以搬运作业为例，根据设定的作业关键点进行轨迹规划，设计基于梯形路径的关键点规划方法，计算各插补点的位姿，并通过运动学逆解得到各关节角度值。经Robotics Toolbox工具箱仿真验证，该算法可以满足机械臂运动平稳、连续的要求，相对于传统矩形规划路径具有距离最优、运动参数更稳定的优势，为下一步将工业机器人空间轨迹同现场工艺参数进行联合规划并实现提供了必要的理论及实践基础。

[1] 杨前明,刘亚琼,王伟,等.基于D-H算法的棉桶更换复合机器人运动学建模与仿真分析[J].组合机床与自动化加工技术,2016(12):52-55.

[2] Bruno Siciliano.机器人手册[M]. 机器人手册编译委员会,译.北京:机械工业出版社,2016.

[3] 任晓平,侯涛,苏建良.仿人双臂多自由度工业机器人设计[J].工业控制计算机,2016,29(11):64-65.

[4] 王鲁平,朱华炳,秦磊.基于MATLAB的工业机器人码垛单元轨迹规划[J].组合机床与自动化加工技术,2014(11):128-132.

[5] Madjid Hank, Moussa Haddad. A hybrid approach for autonomous navigation of mobile robots in partially-known environments[J].Robotics and Autonomous Systems,2016,86(9): 113-127.

[6] 蔡自兴.机器人学基础[M].2版.北京:机械工业出版社,2016.

[7] Guo-Shing Huang. Inverse kinematics analysis trajectory planning for arobot arm[C]. Control Conference,2011: 965-970.

[8] 高帅.工业机器人轨迹规划研究[J].计算机仿真,2015,32(10):409-413.

[9] XIAOYUN DENG. Robot Workcell Modeling and Collision Detection with MATLAB Robotics Toolbox[D].Master of Science Thesis, Tampere University of Technology,2012.

[10] Mark W Spong.机器人建模和控制[M]. 贾振中,译.北京:机械工业出版社,2016.

(编辑李秀敏)

ResearchonTrajectoryPlanningof5-DOFHumanoidManipulatorinJointSpace

ZHANG Cheng1, ZHANG Zhuo2

(1.Zhuhai College of Jilin University, Zhuhai Guangdong 519041, China; 2.Guangdong Polytechnic of Science and Technology, Zhuhai Guangdong 519041, China)

In this paper, the 5-DOF humanoid robot arm is taken as the research object, and the trajectory planning method of industrial robot is discussed. The kinematics of the manipulator is analyzed in this paper, and the kinematics model of manipulator is established. Based on the key points of the task, a trajectory planning method based on joint space five polynomial interpolation algorithm is designed. By using the Robotics Toolbox toolbox, the virtual modeling of the manipulator and the simulation of joint space trajectory planning are carried out. This method can be applied to the trajectory planning of industrial robot, which is of great theoretical and practical significance for the further study of industrial robot control system.

humanoid manipulator; trajectory planning; joint space

TH166;TG659

：A

1001-2265(2017)09-0023-04

10.13462/j.cnki.mmtamt.2017.09.007

2017-02-12；

：2017-03-23

广东省科技发展专项资金(基础与应用基础研究方向)项目(2016A030313658)；广东省工业高新技术领域科技计划项目(2013B010101020)；吉林大学珠海学院创新能力培育工程项目(2016XJCQCX19)；广东科学技术职业学院科研项目(XJPY2016022)；吉林大学珠海学院教学质量工程项目(ZLG20170701)

张程(1986—)，女，沈阳人，吉林大学珠海学院讲师，硕士，研究方向为机器人控制系统，(E-mail)orange1221@163.com。