典型回转闭锁自动机开锁过程动强度数值分析
牟奥敏,徐 诚,唐刘建,杨宇召
(南京理工大学 机械工程学院, 南京 210094)
【装备理论与装备技术】
典型回转闭锁自动机开锁过程动强度数值分析
牟奥敏,徐 诚,唐刘建,杨宇召
(南京理工大学 机械工程学院, 南京 210094)
在设计自动武器时,往往重视闭锁时期零部件的强度而忽视开锁阶段惯性力和碰撞力引起的动强度。针对某枪械回转闭锁机构关键部件在开锁过程中相关零件断裂问题,采用数值分析的方法,建立了枪机、枪机框、开闭锁导柱、击针等零部件开锁过程的惯性应力和撞击应力计算模型。基于仿真结果分析了自动机零部件强度薄弱处的等效动应力情况,为该自动机部件结构的改进提供了理论依据以及数据支撑,也为类似自动机动强度研究提供了分析方法。
自动机强度;数值模拟;惯性应力;闭锁机构
自动机零部件的动强度是枪械设计需要重点考虑的问题,在自动机的诸机构中,开闭锁机构的强度设计尤其重要。回转闭锁机构是枪械常采用的闭锁机构,在对其机构进行设计时,常常重视闭锁时期闭锁支撑面的强度,忽视开锁阶段惯性力和撞击力引起的动强度。其主要原因是闭锁支撑面载荷确定和强度校核较为简单,开锁阶段惯性载荷和撞击力确定非常复杂,动强度校核较为困难。近年来,由于非线性有限元的发展,使得进行回转闭锁机构开锁过程动应力和动强度的计算成为可能。
非线性有限元方法已在枪械行业应用。邹衍等[1]建立了拉机柄在复进过程中受力瞬态弯曲变形的有限元模型,对实验结果和数值计算结果进行了对比分析,发现该有限元模型可以有效地模拟实验中碰撞产生的最大应变;王永娟等[2]建立了考虑由热载荷和压力载荷共同影响的某小口径枪械弹壳弹膛系统的数学和物理模型,采用非线性有限元法数值分析获得了弹壳、弹膛系统在瞬态热载荷和瞬态压力载荷同时作用下弹壳、弹膛系统热应力特性;刘国庆等[3]建立狙击步枪弹头挤进过程有限元计算模型,分析仿真结果得到了多组坡膛锥角与挤进力间的关系,揭示了狙击步枪弹挤进力的作用机理;景银萍等[4]应用大型有限元分析软件对某自动武器的击发过程进行动态仿真,得出该自动武器可靠击发时击针需要具有的能量和速度;张克等[5]使用ABAQUS有限元分析软件,建立起了包含弹壳弹膛系统、迁移式自动机系统的全枪有限元模型,对关键部件进行了强度与刚度分析。但是,关于回转闭锁机构开锁过程的动强度数值计算,未见有公开报道。
本文结合实弹射击中自动机关键部件的破损问题,应用LS-DYNA有限元分析软件建立与之对应的有限元模型[6]、[7],再现了开锁瞬间,自动机各部件发生突然运动和接触碰撞时的受力情况。数值计算获得的危险部位与实验破损情况的一致性较好,从而验证了数值方法的可行性和有效性。在此基础上,进一步分析可能强度薄弱部位的等效动应力大小,给该自动机部件结构的优化提供依据。
1 典型回转闭锁自动机开锁数值计算模型
1.1 开锁过程简述
某枪械回转闭锁自动机开锁过程[8-9]如图 1所示。在开锁自由行程的起点(图 1(a)),火药气体压力通过活塞作用于枪机框的前端面,枪机框在火药气体压力的作用下向后运动;枪机框中的开闭锁螺旋槽带动开闭锁导柱与枪机转动;在开锁行程的终点,枪机框以6 m/s的速度与开闭锁导柱发生碰撞(该速度由高速摄影测得),开闭锁导柱与枪机以3 rad/s的速度顺时针自转;此时,枪机的闭锁突榫由于自转而与节套的闭锁支撑面解脱,枪机与开闭锁导柱在接触力和碰撞力的作用下与枪机框一起后坐。在开锁行程的终点,枪机框撞击开闭锁导柱,该碰撞力可能造成枪机框与开闭锁导柱相关部位破损;开闭锁导柱在接触力和碰撞力的作用下带动枪机突然运动,开闭锁导柱与枪机之间的相互作用力可能造成开闭锁导柱与枪机相关部位破损。本文针对开锁行程终点时刻自动机各零部件的运动特性建立数值计算模型,重点关注开锁过程和开锁行程终点自动机各相关零部件之间的惯性力与碰撞力的作用,研究自动机各相关零部件的破损情况。
1.2 有限元模型
建立自动机部件在开锁行程终点瞬间,枪机框撞击开闭锁导柱带动枪机后坐时刻的有限元模型,在对数值模拟结果影响不大的情况下对几何模型进行简化,以提高计算效率。模型各部分名称见图2。为了提高计算效率,将枪机框与仿真结果影响不大的部分略去,以质量补偿模块取代。自动机部件皆采用四面体网格模型。采用*INITIAL_VELOCITY_GENERATION关键字赋予枪机框6 m/s的初始速度(该初始速度由高速摄影所得,为枪机框开锁行程终点的真实速度);由于开闭锁螺旋槽的存在,枪机与开闭锁导柱相对于枪机框转动,根据开闭锁螺旋槽的角度,计算出枪机与开闭锁导柱相对枪机框的转速3 rad/s,并采用*INITIAL_VELOCITY_GENERATION关键字赋予枪机与开闭锁导柱;各个部件之间采用*CONTACT_AUTOMATIC_SURFACE_TO_SERFACE定义接触,该接触类型适用于可以预见的两表面之间的接触。

图2 自动机部件有限元模型
1.3 材料模型
自动机部件采用JOHNSON_COOK材料模型[10]和GRUNEISEN状态方程描述其材料特性。该模型综合考虑了材料的应变强化、应变率效应和热软化效应,特别适合模拟金属材料在高加载率下的动态响应。自动机部件材料模型参数如表1所示。
质量补偿材料也采用表 1所列的材料参数数据,但材料密度不同,保证枪机框的总质量与几何模型修改之前相等。

表1 自动机部件材料参数
2 数值结果分析
借助仿真结果,可以方便的再现该枪械开锁行程各零部件碰撞的过程,获得开锁过程中自动机各部件不同时刻、不同位置时的等效动应力。
2.1 枪机动应力变化情况
枪机在不同时刻的von Mises应力云图如图3。在枪机与开闭锁导柱配合处的von Mises应力明显比枪机其他区域要大,故该处是枪机上强度薄弱的区域。枪机在仿真全过程的最大应力为1200MPa左右,最大应力出现在枪机与开闭锁导柱配合的圆孔位置。结合材料的屈服极限,由仿真结果可推断该处网格单元可能已经屈服。

图3 枪机von Mises应力云图
该枪械在五连发射击试验过程中,存在枪机断裂的情况。枪机断裂图如图4。从图中可以看出,枪机与开闭锁导柱配合处圆孔发生断裂,实际断裂截面与理论强度最薄弱截面存在一个偏角。存在偏角的原因是枪机有自转;仿真结果中,高应力单元的分布也存在一个偏角。对比仿真所得应力云图与实弹射击试验中枪机的断裂情况,仿真结果显示的危险截面与实际结果吻合较好,所得仿真结果具有实际参考价值。
枪机断裂处选定单元的等效动应力(von Mises应力)随时间的变化曲线如图5所示。开闭锁导柱与枪机的碰撞发生在第20 μs,碰撞发生后等效应力开始攀升,经过大概15 μs的时间,等效动应力达到最大值1 200 MPa,然后以1 200 MPa保持大约10 μs左右的时间。此后等效动应力开始下降到800 MPa左右,然后重新攀升到1 200 MPa左右,之后等效动应力开始下降,最低时为50 MPa左右,然后等效应力值继续有一个回升。从等效应力数值的变化可以看出,开锁行程终点枪机与开闭锁导柱应该有多次的碰撞,在30 μs到75 μs的时间段内,等效动应力的数值都处于800 MPa以上。

图4 枪机断裂图

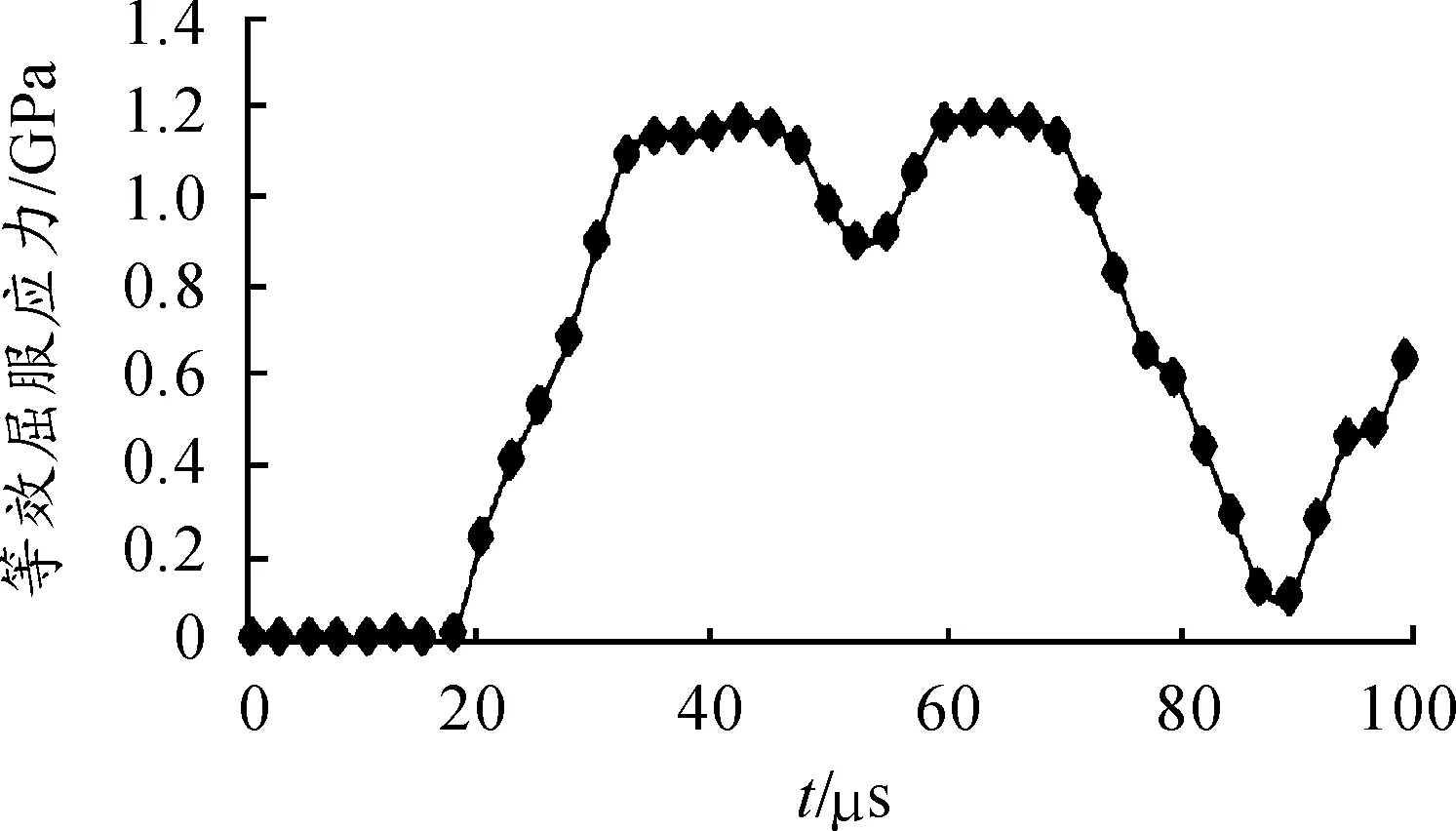
图5 枪机断裂处选定单元的von Mises应力随时间变化曲线
2.2 枪机框动应力变化情况
枪机框部件的von Mises应力云图如图6。不难发现,枪机框上存在三处危险部位。危险部位1是开闭锁导柱与枪机框发生碰撞的位置;危险部位2是直接受碰撞所产生的应力波冲击的位置;危险部位3是枪机框上厚度最薄的位置,撞击产生的应力波传播到此处也可能破坏此处结构。从理论上分析,这三处也是最可能发生塑性变形的位置。
该枪械在五连发射击试验过程中,发现枪机框上有些位置出现了裂纹。图7为其中一处裂纹的照片,该处裂纹出现在危险部位1与危险部位2的连线上。危险部位3处也有裂纹出现,但是裂纹较细,无法在图片中显示。对比仿真结果与枪机框实弹射击后的裂纹情况,二者结果能较好的吻合,所得仿真结果具有实际参考价值。
枪机框危险部位选定单元von Mises应力随时间变化曲线如图8。A单元von Mises应力的最大值为780 MPa,这个值是三个单元中最大的,该应力数值与屈服极限非常接近;B单元von Mises应力的最大值与C单元的von Mises应力最大值差不多大,都为590 MPa左右。相对于枪机上的von Mises应力,枪机框上的von Mises应力情况要稍好一些,最大von Mises应力在材料屈服极限之内。由于每一发弹的装药量存在差别,个别枪弹在发射时所产生的膛压可能比一般情况要大,导致枪机框的开锁速度变大产生裂纹。

图6 枪机框von Mises应力云图

图7 枪机框裂纹


图8 枪机框危险部位选定单元von Mises应力 随时间变化曲线
2.3 开闭锁导柱动应力变化情况
开闭锁导柱不同时刻的应力云图如图9。从图中可以看出,开闭锁导柱应力较大的位置为开闭锁导柱与枪机框碰撞部位,该部位有可能存在塑性变形。经实弹射击后,开闭锁导柱没有出现断裂或存在裂纹的情况,但是开闭锁导柱上出现一条撞击纹路与仿真结果中的高应力单元分布区域相吻合。开闭锁导柱危险部位选定单元von Mises应力随时间变化曲线如图11所示。从图中可以看出,选定单元的最大应力为800 MPa左右,达到材料的屈服极限所以该处有可能存在塑性变形,是危险部件。

图9 开闭锁导柱von Mises应力云图
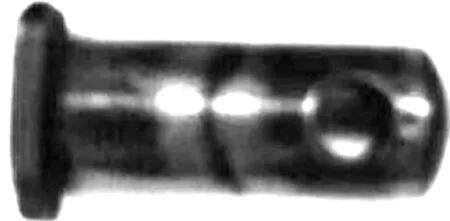
图10 实弹射击后的开闭锁滚柱


图11 开闭锁导柱危险部位选定单元von Mises应力 随时间变化曲线
3 结论
建立了本回转闭锁自动机开锁过程有限元计算模型,计算获得的零部件危险部位与实弹射击零部件破损情况基本一致,验证了模型的正确性。数值计算表明,开锁过程中枪机最大动应力出现在与开闭锁导柱配合的圆孔处,在第40 μs时达到最大应力值,为1 200 MPa;枪机框最大动应力出现在枪机框与开闭锁导柱直接碰撞的部位,在第65 μs时达到最大应力值,为780 MPa;开闭锁导柱最大动应力出现在与枪机框碰撞的部位,在第75 μs时达到最大应力值,为800 MPa。本文计算揭示了该回转闭锁自动机开锁过程关键部件的损坏机理,为该自动机零部件结构改进提供了科学依据,也为类似自动机开锁过程动强度研究提供了分析方法。
[1] ZHOU Yan,WANG Yaping,LUO Shaomin,et al.Experiment and numerical research of transient response under Inertia effect of firearm cocking handle[C]//2015 2nd International Conference on Simulation and Methodologies,Technologies and Applications(SMTA 2015).
[2] 王永娟,赵军,唐竹秀.压力载荷与温度场作用下弹壳弹膛系统的动态响应[J].兵工学报,2010,31(6):669-673.
[3] 刘国庆,徐诚.狙击步枪弹准静态弹头挤进力研究[J].兵工学报,2014,35(10):1528-1535.
[4] 景银萍,杨臻.有限元仿真在枪械击发中的应用[J].机械工程与自动化,2007(3):48-49.
[5] 张克,袁点.微后坐冲锋枪全枪有限元仿真研究[J].四川兵工学报,2015,36(12):1-5.
[6] 白金泽.LS-DYNA3D理论基础与实例分析[M].北京:科学出版社,2005.
[7] 赵海欧.LS-DYNA动力分析指南[M].北京:兵器工业出版社,2003.
[8] 王裕安,徐万和,薄玉成.自动武器构造[M].北京:北京理工大学出版社,1994.
[9] 欧学炳,殷仁龙,王学颜.自动武器结构设计[M].北京:北京理工大学出版社,1994.
[10] JOHNSON G R,COOK W H.A constitutive model and data for metals subjected to large strains,high strain rates and high temperature[C]//Proceedings of the 7th International Symposium on Ballistics.Hague,Netherlands:IBC,1983:541-526.
(责任编辑周江川)
NumericalAnalysisofDynamicStrengthofTurningBlockAutomaticMechanismatUnlockingTime
MOU Aomin, XU Cheng, TANG Liujian, YANG Yuzhao
(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)
Turning block automatic mechanism spare parts are important parts of turning block automatic weapon,and they require a high safety factor. During the design of an automatic weapon,more importance has been attached to the strength of the spare parts at locking time,but the dynamic strength problems caused by inertia force and impact force during unlocking time often were ignored. Aimed at the problem that a firearm turning block mechanism’s key component fractured at the locking time, a computational model is built by using numerical analysis method to compute inertia force and impact force of action, action frame, lock and unlock column, firing pin during locking time. Based on simulation results, the equivalent dynamic stress of the weak parts of automatic mechanism spare parts has been obtained. The results of the simulation can provide theoretical basis and data support for the improvement of the automatic mechanism spare parts’ structure.
automatic mechanism’s strength; numerical analysis; inertia force; locking mechanism
2017-03-29;
:2017-05-06
:企业合作项目
牟奥敏(1992—),男,硕士研究生,主要从事自动武器数值模拟研究。
徐诚(1962—),男,博士,教授,南京理工大学机械工程学院博士生导师,轻武器学会副主任委员、兵工学报编委。
10.11809/scbgxb2017.09.011
format:MOU Aomin, XU Cheng, TANG Liujian, et al..Numerical Analysis of Dynamic Strength of Turning Block Automatic Mechanism at Unlocking Time[J].Journal of Ordnance Equipment Engineering,2017(9):53-57.
TJ23
:A
2096-2304(2017)09-0053-05
本文引用格式:牟奥敏,徐诚,唐刘建,等.典型回转闭锁自动机开锁过程动强度数值分析[J].兵器装备工程学报,2017(9):53-57.

