基于时间序列神经网络的山核桃化学成分分析1)

栗晓禹 黄兴召

(国家林业局调查规划设计院，北京，100714) (安徽农业大学)

基于时间序列神经网络的山核桃化学成分分析1)

栗晓禹 黄兴召

(国家林业局调查规划设计院，北京，100714) (安徽农业大学)

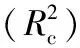
核桃；蛋白质；脂肪；时间序列神经网络法；神经网络法；偏最小二乘法

山核桃(CaryacathayensisSarg.)是我国特有的高档干果和木本油料树种，主要分布于浙、皖交界的天目山区。有近7万农户从事山核桃生产经营，主产区农户的收入70%以上来源于山核桃[1]。山核桃的营养成分含量是评价山核桃质量好坏的重要指标。因此，对果实的化学成分(脂肪、蛋白质、氨基酸等)含量分析具有重要的价值。王冀平等[2]较早的利用氨基酸分析仪和气相色谱仪及经典的化学分析法对山核桃仁中的氨基酸、脂肪酸、蛋白质、脂肪的组成和含量进行了测定。同时，也对山核桃外果皮的化学成分的进行了测定和分析[3-4]。山核桃化学成分的测定过程复杂，费时费力。但是，运用光谱数据与植物生理特性的相关性，分析果实的化学成分含量，方法简单、操作快速，越来越受到重视[5-7]。

偏最小二乘法(PLS)能够在自变量存在严重多重相关性的条件下进行回归建模，并且在样本点个数少于变量个数的条件下进行线性回归[8]。但是，样本数据变异范围较大时，样本数据和光谱参数的非线性关系就会增大，预测效果就会变差[9]。人工神经网络(ANN)从信息处理的角度，对人脑神经元网络进行抽象，建立简单模型，按不同的连接方式组成不同的网络，通过模拟大脑神经网络处理、记忆信息的方式进行信息处理[10]。ANN是由大量处理单元互联组成的非线性、自适应信息处理系统，同时，将PLS分析中得到的特征变量作为ANN的输入参考，不仅减少了ANN的计算量，加快训练速率，还可以去除光谱干扰，提高预测效果[11]。偏最小二乘法的人工神经网络(PLS-ANN)方法可以很好的利用光谱数据预测样品的化学成分[12]。

山核桃化学成分的含量随着果实的生长不断增加，利用PLS-ANN预测山核桃果实生长过程中化学成分的变化，必须考虑时间因素。因为山核桃果实化学成分含量的变化与时间序列(TS)具有典型非线性相关。因此，可以通过前期的果实脂肪含量，预测后期的果实脂肪含量。时间序列的神经网络(TSNN )作为一种非参数的方法，利用前期的数据来识别隐含着时间序列中的相关性和记忆效应，解决有时间序列的预测问题[12]。因此，通过测定6个时间梯度的山核桃果实的蛋白质和脂肪含量，利用PLS、PLS-ANN和TSNN等方法建模，预测山核桃果实蛋白质和脂肪含量，以期为经济林果实成分分析提供新的数据处理方法。

1 研究地概况

实验地点位于安徽省金寨县山核桃示范园，地处安徽省西部，大别山主脉北坡,该区属北亚热带季风湿润季候，年平均气温16 ℃，全年无霜期210 d，年降水量1 400 mm,土壤为典型的沙壤土，土壤厚度≥60 cm，pH值6.0～6.5。

2 研究方法

2.1 实验样品及化学成分测定

实验所需山核桃样品的采集地点为安徽省金寨县山核桃示范园，据果实生长发育过程将采集样品分为6个时间梯度：2014年7月21日、8月1日、8月11日、8月21日、8月31日和9月10日。每个时间梯度的间隔均为10 d， 每次采集15颗山核桃果实，带到实验室进行分析。

山核桃果实蛋白质含量采用凯式定氮法测定。每颗山核桃经破壳、取仁、粉碎均匀后，其中取1 g置于 500 mL燥的凯氏烧瓶内，利用CuSO4、K2SO4、浓硫酸、2%的H3BO3、甲基红-溴甲酚混合指示剂、饱和氢氧化钠溶液和0.01 mol/L的HCl标准滴定液，测定每个果实的蛋白质质量分数。

山核桃果实脂肪质量分数采用酸水解法测定。取粉碎均匀的果仁2 g置于50 mL试管内，通过浓盐酸、乙醚、石油醚和5%乙醇，使用水浴锅、具塞量筒和干燥箱提取脂肪，根据样品质量及提取的脂肪质量计算每个果实的脂肪质量分数。

2.2 样品光谱数据

山核桃经破壳、取仁、粉碎均匀后剩余的样品，使用美国ASD公司的FieldSpec3 型光谱仪(350～2 500 nm)进行样品测试每颗山核桃样品。采样间隔在350～1 000 nm为1.4 nm，1 000～2 500 nm为2 nm。整个过程都在暗室中进行，以卤素灯为唯一光源，最大限度减小外来光线的影响[13]。光源入射角45°，距样品表面30 cm，探头位于山核桃果仁样品垂直上方15 cm处，视场角45°，果仁样品覆盖面积20 cm2。每个样本取10条光谱曲线数据算术平均，得到该山核桃果仁样品实际反射光谱数据；每测8个样本做一次白板校正，以获得无量纲的相对反射率。

山核桃果仁的光谱图有一定的共性，即本身的特征性和指纹性(见图1)。不同时间梯度的山核桃果仁的光谱图有明显区别。除了350～450 nm 和900～1 400 nm的光谱有重叠外，在450～750 nm和1 800～2 500 nm 的光谱有明显的差异。

图1 山核桃果实发育阶段的6个时间梯度的光谱图

2.3 预测方法

偏最小二乘法(PLS)：采用 PLS 对山核桃样品的实际反射光谱数据进行降维和正交化处理，得到原始数据矩阵的 PLS 主成分及相应的主成分得分矩阵[14]，并建立 PLS 回归模型，对山核桃果实样品中的蛋白质和脂肪含量进行预测。

偏最小二乘法的人工神经网络(PLS-ANN)：ANN中处理典型的单元类型如图2所示，输入层、隐藏层和输出层。输入层接受实验测定的光谱数据，输入向量X包含M维数据；隐藏层是处在输入和输出单元之间，不能由系统外部观察的单元，包含H个单元；输出层实现处理结果，输出向量Y包含N维数据。输入层与隐藏层之间的连接权值为wij，隐藏层与输出层之间的连接权值为wjk，其中i∈[1，M]，j∈[1，H]，k∈[1，N]。利用样本中的导出值得到输出层误差，然后根据德尔塔法则，在网络中反向传播误差来修正网络中的各层误差，反复这个过程直到网络的输出误差符合期望误[15]。

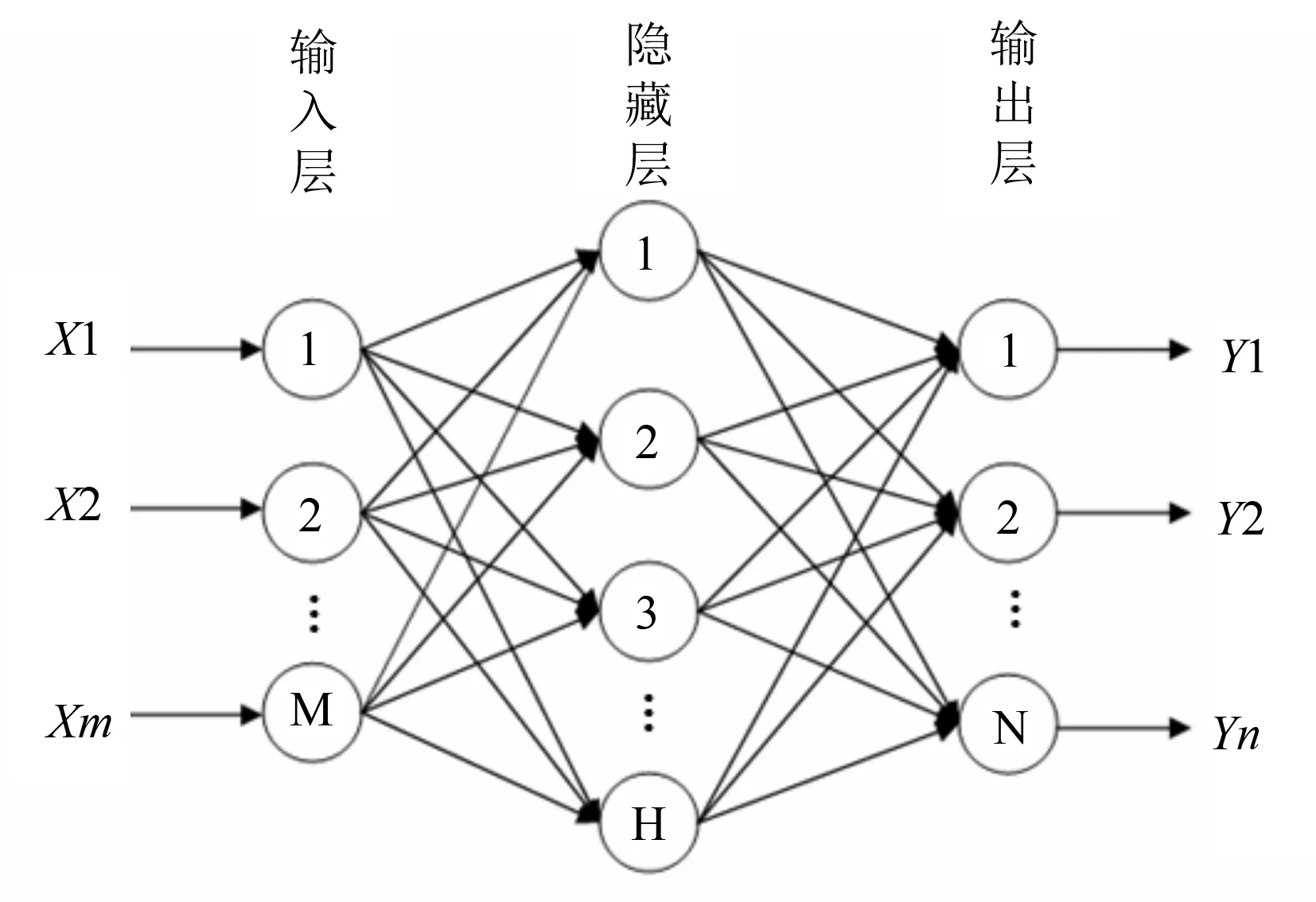
图2 人工神经网络示意图

本研究中PLS-ANN网络输入层、隐藏层和输出层节点数分别为8、11、1。输入层节点为PLS 主成分个数，输出层设定的输出值分别为[0, 1]和[0.1, 0.9]，最小训练速度为0.4，迭代次数设定为1 000次。

时间序列的神经网络(TSNN)：TSNN方法的关键是规格化处理，可以有效防止数值范围过大使激活函数失去作用[16]。以山核桃化学成分含量预测为例，因数据来源于不同时间梯度的观测点，故需要对数据进行整合，以代表山核桃蛋白质或脂肪含量的变化情况。然后对数列进行归一化处理，以加快网络的收敛速度。山核桃蛋白质或脂肪含量的归一化处理，是将数列值与最小序列值做差，除以序列最大值与最小值之差，数列就转化到[0, 1]或者[0.1, 0.9]。

TSNN用于时间序列的预测，其方法就是按照固定长度分割样本，本研究样本的固定长度为10 d，使每一个样本都对应着1个或多个未来的序列值，每一个样本输入人工网络就得到一个输出，输出值就是样本对应的未来序列的预测值，通过与真实值的对比，训练网络最终达到预测时间序列的目的[17]。

TSNN数学表达如下：

式中：aj、βij分别是神经网络的连接权重，i=0、1、2、…、h，j=0、1、2、…、n，n和h分别是网络的输入层及隐藏层节点数。

基于时间序列的神经网络的数学表达式，本质上是一个对于过去时间序列(yt-1，yt-2，yt-3，…，yt-h)到未来时间(yt)的一个非线性函数，即：yt=f(yt-1，yt-2，yt-3，…，yt-h)+wt。其中：函数f(x)代表了TSNN的结构和连接权重因素，TSNN的权重参数为wt。TSNN网络输入层、隐藏层和输出层节点数、输出层设定输出值、最小训练速度及迭代次数与ANN相同。

3 结果与分析

表1 3种方法预测山核桃蛋白质质量分数的检验

由图3可知，PLS方法的误差较大，大部分蛋白质质量分数预测值离回归线较远；PLS-ANN方法优与PLS方法，预测值大部分分布在回归线两侧；TSNN方法最优，预测值均匀分布在回归线上。因此，说明TSNN方法较好，且预测精度最高。

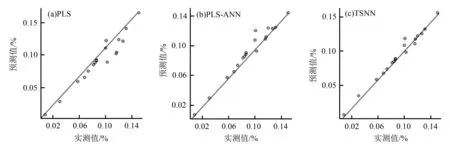
图3 山核桃蛋白质质量分数的预测值和实际值的散点图

表2 3种方法预测的山核桃脂肪质量分数的检验

由图4可知，PLS方法预测的脂肪质量分数误差较大，大部分脂肪质量分数预测值离回归线较远；PLS-ANN方法优与PLS方法，脂肪质量分数预测值大部分分布在回归线两侧；TSNN方法最优，脂肪质量分数预测值均匀分布在回归线上，说明TSNN方法最优，且预测精度最高。

图4 山核桃脂肪含量的预测值和实际值的散点图

4 结论与讨论

本文偏重拟合方法研究，利用偏最小二乘法(PLS)，人工神经网络(PLS-ANN)和时间序列的神经网络(TSNN)3种方法，分别拟合山核桃果实蛋白质和脂肪的含量，TSNN可以消除果实生长发育过程中时间对其影响，显著提升山核桃果实在生长发育过程中蛋白质和脂肪含量的估算效果。KHALED 等[12]、HAROLD 等[15]在林分物理化学性质、果实的养分含量等指标的预测中，表明人工神经网络(PLS-ANN)和偏最小二乘法(PLS)之间存在显著差异，且PLS-ANN可以提升预测精度。因为，PLS-ANN是由大量处理单元互联组成的非线性、自适应信息处理系统，按不同的连接方式组成不同的网络，通过模拟大脑神经网络处理、建立某种简单模型，不仅减少了计算量，还可以去除光谱干扰。

山核桃蛋白质和脂肪的含量，随着果实的生长不断增加，预测模型必须考虑时间因素。时间序列的神经网络(TSNN)按照时间长度将样本分割，进行规格化处理，防止数值范围过大使激活函数失去作用[17]。不同时间段的山核桃蛋白质和脂肪含量，在TSNN中以时间梯度进行了行归一化处理，以加快网络的收敛速度。因此，消除时间梯度对山核桃蛋白质和脂肪含量预测的影响，提升了预测精度。

基于山核桃果实发育阶段的6个时间梯度的光谱图，分别使用PLS方法、PLS-ANN方法和TSNN方法预测山核桃果实蛋白质和脂肪的含量，TSNN的预测均方根误差最小。因此，TSNN方法分析时间梯度的数据时，具有较好的预测能力和稳健性。

[1] 黄坚钦，夏国华.图说山核桃生态栽培技术[M].杭州：浙江科学技术出版社,2008:36-41.

[2] 王冀平，李亚南，马建伟.山核桃仁中主要营养成分的研究[J].食品科学,1998,19(4):44-46.

[3] 林君阳.山核桃外果皮化学成分及抑菌活性研究[D].临安:浙江林学院,2008：32-35.

[4] 陈仕云，吴德玲，金传山，等.山核桃外蒲壳化学成分初步分析及总黄酮含量测定[J].安徽中医药大学学报,2010,29(1):64-66.

[5] 顾志宏.基于高光谱的大麦籽粒蛋白质含量遥感预测[J].光谱学与光谱分析,2012,32(2):435-438.

[6] AITHALA K B, KUNMAR S M R, RAO N B, et al. Juglone, a naphthoquinone from walnut, exerts cytotoxic and genotoxic effects against cultured melanoma tumor cells[J]. Cell Biology International,2009,33(10):1039-1049.

[7] 叶旭军,KENSHI S,何勇.基于机载高光谱成像的柑橘产量预测模型研究[J].光谱学与光谱分析,2010,30(5):1295-1300.

[8] RÖNKKÖ M, MCINTOSH C N, ANTONAKIS J. On the adoption of partial least squares in psychological research: Caveat emptor[J]. Personality and Individual Differences,2015,87:76-84.

[9] HAZAMA K, KANO M. Covariance-based locally weighted partial least squares for high performance adaptive modeling[J]. Chemometrics and Intelligent Laboratory Systems,2015,146:55-62.

[10] ATA R. Artificial neural networks applications in wind energy systems: a review[J]. Renewable and Sustainable Energy Reviews,2015,49:543-562.

[11] MAXIME J, JULIEN P, PIERRICK N, et al. Fractionation in position-specific isotope composition during vaporization of environmental pollutants measured with isotope ratio monitoring by 13C nuclear magnetic resonance spectrometry[J]. Environmental Pollution，2015,205：299-306.

[12] KHALED C, EDDY E T, LOUBNA B, et al. Predicting the flame characteristics and rate of spread in fires propagating in a bed of pinus pinaster using artificial neural networks[J]. Process Safety and Environmental Protection,2015,98:50-56.

[13] EUNYOUNG C, FREEK M, FRANK R, et al. Mapping of heavy metal pollution in stream sediments using combined geochemistry, field spectroscopy, and hyperspectral remote sensing: A case study of the rodalquilar mining area, SE Spain[J]. Remote Sensing of Environment,2008,112(7):3222-3233.

[14] MAJID B， SAYED A M， ZAHRA B. Modeling and optimization of activated sludgebulking for a real wastewater treatment plant using hybrid artificial neural networks-genetic algorithm approach[J]. Process Safety and Environmental Protection,2015,95:12-25.

[15] HAROLD W W, DANIEL S J C, BRUCE D B, et al. Testing complex models with small sample sizes a historical overview and empirical demonstration of what partial least squares (PLS) can offer differential psychology[J]. Personality and Individual Differences,2015,84:73-78.

[16] LEONEL A L, RICARDO A S F, GUILHERME G L. Maximum and minimum stock price forecasting of brazilian power distribution companies based on artificial neural networks[J]. Applied Soft Computing,2015,35:66-74.

[17] HU Z Y, BAO Y K, CHIONG R, et al. Profit guided or statistical error guided? a study of stock index forecasting using support vector regression[J]. Journal of Systems Science and Complexity,2017(2):1-18.

NeuralNetworkofTimeSeriesinChemicalContentofHickory//

Li Xiaoyu
(Academy of Inventory and Planning, SFA, Beijing 100714, P. R. China);
Huang Xingzhao
(Anhui Agricultural University)//Journal of Northeast Forestry University，2017,45(9)：54-57.

CaryacathayensisSarg.; Protein; Fat; Neural network of time series; Artificial neural networks; Partial least squares

S715.3

1)林业行业标准(2017-LY-086)；林业科普项目(2017-KP13)；安徽农业大学青年项目(2014rz013)。

栗晓禹，女，1982年7月生，国家林业局调查规划设计院，工程师。E-mail:lixiaoyu@afip.com.cn。

黄兴召，安徽农业大学林学与园林学院，讲师。E-mail:xingzhaoh@163.com。

2017年6月19日。

责任编辑：王广建。

We proposed a neural network of time series method (TSNN), and compared with the partial least squares (PLS) and the artificial neural networks of partial least squares (PLS-ANN) to test the results of modeling and prediction. The measured data of spectra and proteins and fat contents in six growth stages were studied. The PLS, PLS-ANN and TSNN method were used to establish the model, and the results were compared. For the contents of protein, the root mean square error (RMSEP) of the TSNN was reduced by 18.82% and 7.39% PLS and PLS-ANN, respectively. For the contents of fat, the RMSEP of the TSNN were reduced by 39.95% and 35.02% compared with PLS and PLS-ANN, respectively. The correlation coefficient squared and the prediction correlation coefficient squared of TSNN were improved compared with PLS and PLS-ANN.