鼓励一题多解，开拓学生的思维

文湛江一中培才学校 姚 琳 麦 良

鼓励一题多解，开拓学生的思维

文湛江一中培才学校 姚 琳 麦 良

数学问题的解决途径，往往是多角度、多方面的，而要进行多角度思考，学生必须先掌握基础知识，其次则要对这些知识之间的联系有充分的认识。在当前应试教育的压力下，我们在教学中容易存在这样的误区：热衷于升学率，开展机械化练习。呆板的教学模式，学生只有被动地接受知识，对知识却“不知所以然”，容易形成 “不授不会，新题不会”的局面，最终使得学生对数学的学习失去信心。我们应该走出误区，培养学生灵活运用知识解决问题的能力。

一、一题多解的培养方式

1.重视基础，识别概念

数学是由众多概念、定理构成的体系，已知的概念和定理是推理的根据。不管多么复杂的数学问题，它都是由若干个基础知识整合而成的，因此学生只有掌握了这些基础知识，一题多解才能继续进行，否则，只能导致推理的错误。为此，课堂教学中，教师应注重基础知识的讲解，特别是容易混淆的知识点。

2.数形结合，寻求突破

数学是千变万化的，但又万变不离其宗。有时候遇到几何问题，当你无从下手的时候，从代数的角度出发，可能会柳暗花明又一村。

例：如图1，在平面直角坐标系中，已知O为原点，四边形ABCD为平行四边形，A、 B、 C的坐标分别是A点D在第一象限．

图1

（1）求D点的坐标；

（3）求平行四边形ABCD与四边形A1B1C1D1重叠部分的面积？

解： （1）由B、C的坐标可知，AD=BC=4，则可得点D的横坐标为1，点D的纵坐标与点A的纵坐标相等，为2，可得点D的坐标为 （1，2）。

（2）依题意得A1、B1、C1、D1的坐标分别为

（3）如图2，平行四边形ABCD与四边形 A1B1C1D1重叠部分的面积为平行四边形DEB1F的面积

图2

由题意易得∠FA1N=∠FB1M，∠A1NF=∠B1MF=90°，A1N=B1M=

∴△B1MF≌△A1NF（AAS）

1│xB│）

∴平行四边形DEB1F的边

DF=xD-xA1-NF=-

平行四边形DEB1F的高为

B1M=2

本题的难点主要在于第3小问，初步主要考查平行四边形的性质，坐标与图形的性质及坐标与图形的平移问题，但仔细思考，如能进行数形结合，采用一次函数观点解题，又有另一番景象。

解： （3）如图，平行四边形ABCD与四边形A1B1C1D1重叠部分的面积为平行四边形DEB1F的面积

图3

设直线A1B1解析式为y=kx+b（k10）

解得

∴直线A1B1解析式为 y=2

∴平行四边形 DEB1F的边DF=xD-xF=

平行四边形 DEB1F的高为B1M=2

3．陌路相遇，解决困境

数学是一门灵活的学科，知识点间的关系千丝万缕，往往表面看似无关，但内里暗含玄机，只要把握住题目所能牵出的关联点，在解题过程中就可赢得时间和计算上的简便。

例：如图4，在Rt△ABC中，∠C=90°，AB，BC，CA的长分别为c，a，b，求△ABC的内切圆⊙O的半径。

解：如图5，⊙O内切于Rt△ABC中，切点为D、E、F，连结AO、BO、CO、DO、EO、FO，则设⊙O半径为r

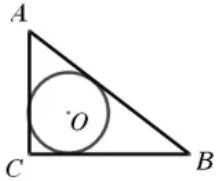
图4

图5

∴OD=OE=OF=r，OD⊥AC，OE⊥BC，OF⊥AB

∵SRt△ABC=AC·BC=ab

且 SRt△ABC=S△BOC+S△AOC+S△AOB

△BOC△AOC△AOB

△BOC

△AOC

△AOB

△BOC△AOC△AOBcr=ab

本题考查了三角形的内切圆、三角形的面积等知识，但如果联系圆本章的切线长定理和之前正方形的内容，本题又有另一番景象。

解：如图6，⊙O内 切 于 Rt△ABC中，切点为D、 E， 连结OD、OE、OF，则设⊙O半径为r

图6

∴OD=OE=OF=r，且OD⊥AC，OE⊥BC，OF⊥AB

∴∠C=∠ODE=∠OED=90°

∴四边形CEOD是矩形

∵OD=OE

∴矩形CEOD是正方形

∴CE=CD=OD=r

∴AD=b-r,BE=a-r

又∵⊙O内切于Rt△ABC中，切点为D、E、F

根据切线长定理有AD=AF, BE=BF

∴AB=AF+BF=AD+BE=b-r+ar=a+b-2r

又∵AB=c

二、事半功倍的教学效果

在初三复习课的教学中，例题的选取显得尤为重要。一道好的例题，即便题目简单，它也能像一部情节曲折的电影，跌宕起伏中透漏出真相。当 “山重水覆”的困惑被“柳暗花明”的喜悦取代之后，学生又怎能不增添多几分信心呢？

例：如图7，在△ABC中，AD= BD=CD， 求 证 ：△ABC是直角三角形。

图7

证法1：如图1

∵AD=CD，CD=BD

∴∠1=∠A，∠2=∠B

在△ABC中，∵∠A+∠B+∠ACB=180°

∴∠A+∠B+∠1+∠2=180°

∴2（∠1+∠2）=180°

∴∠1+∠2=90°

即∠ACB=90°

∴△ABC是直角三角形

这种证明方法说明了 “如果一个三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形”。

证法2：如图8，延长AC到E使CE=AC，连接BE．

图8

∵AD=BD

∴CD 是△ABE的中位线

∴AB=BE

∴BC⊥AC

∴△ABC是直角三角形．

这种证法利用了等腰三角形“三线合一”的性质，在完成例题的同时又复习了这一性质。

证法3：如图9

图9

设AC=b，BC=a，AB=c，取BC中点E，连接DE．

∴DE是△ABC的中位线．

∵CD=BD，∴DE⊥BC。

在Rt△DEB中，∵DE2+BE2= BD2，

∴a2+b2=c2，∴△ABC是直角三角形。

这种证法利用了勾股定理的逆定理。

三角形的知识点有很多，在复习课上如何让学生牢记并运用这些性质定理，是复习的关键。如果直接复习讲定理，易显得枯燥无味，特别是在初三复习课中，周而复始的讲会让学生觉得很烦，但由学生自己推理得到，就能加深印象，有利于复习。而由于课堂时间有限，不可能讲很多题，此时小组合作一题多解便打开了新的大门。所谓是“横看成岭侧成峰”，一道题，不同的人有不同的想法，在合作的过程中让学生自行领悟方法，进行学法交流，从不同方法中领悟到不同的知识点。

[本论文是广东省教育科研“十二五”规划2013年度研究一般项目 （批准号2013YQJK246）课题成果之一。有删改]

责任编辑 王思静