列车荷载作用下地基动力及沉降特性分析

陈 俊

(吉河高速公路建设管理处，山西 临汾 041699)

列车荷载作用下地基动力及沉降特性分析

陈 俊

(吉河高速公路建设管理处，山西 临汾 041699)

为分析列车荷载作用下的地基动力及沉降特性，建立了轨道-路堤-地基在列车荷载作用下的动力耦合分析数值模型，考虑列车速度、路堤高度和基床刚度的影响，研究了列车荷载作用下的地基动应力分布及地表沉降特性，并对不同地基加固形式的加固效果进行了探讨。研究结果表明：列车荷载作用下地基动应力沿水平方向和地基深度迅速减小；地基竖向动应力和地基沉降随列车速度的增大而增大，随路堤高度和基床刚度的增大而减小，路堤高度不宜小于2 m；地基沉降随加固深度和加固区刚度增大而减小，列车速度越高，影响越明显，最佳地基加固深度为3 m。

铁道工程；列车荷载；数值模拟；地基动应力；地基沉降；地基加固

0 引 言

高速铁路列车的高速运行会对轨道和路基造成很大的冲击振动，进而导致路基变形和不均匀沉降的不断累积，严重影响列车运行的平顺性、舒适性和安全性[1-2]。相比于普通铁路，高速铁路对基床厚度、填料参数和压实标准等提出了更高要求，当上述参数满足规范要求时，路基动力及变形控制的关键在于地基，列车荷载作用下的地基动力和变形控制己成为高速铁路路基设计的关键难点之一。

普通铁路路基设计在考虑列车荷载时，通常采用换算土柱法将静荷载和动荷载一并简化为等效静荷载加以处理，这种简单采用静力学的观点在分析实际路基的动力稳定性及长期附加沉降时具有很大局限性；T.EKEVID等[3]采用边界元分析了高速列车移动引起的波在周围路基中的传播特征，建立了考虑路基无限边界的地基振动模型；R.PAOLUCCI等[4]将列车与轨道分离，建立了轨道-路基结构的二维和三维分析模型；蔡英等[5]研究了铁路路基的动应力、永久变形和弹性变形随列车轴重、运行速度及列车荷载作用次数的变化规律，提出了改善路基动力特性的措施；董亮等[6]基于三维有限元轨道-路基动力模型，计算得到了列车荷载作用下沿路基深度分布的动偏应力。

笔者通过建立轨道-路堤-地基在列车荷载作用下的动力耦合分析数值模型，考虑列车速度、路堤高度和基床刚度的影响，研究列车荷载作用下地基的动力及沉降特性，并对不同地基加固形式的加固效果进行探讨。

1 数值模型的建立

1.1 计算模型及边界条件

由于路基具有对称性，可取半幅路基结构建立三维有限元模型进行分析，以有效减少数值模型单元数量和计算时间[7]。数值建模采用大型有限元程序ABAQUS，模型主要包括轨道板、道碴、基床表层、基床底层、路堤和地基5个部分，路堤断面尺寸参照TB10621—2014《高速铁路设计规范》[8]确定，如图 1，不考虑下卧层变形和地下水的影响。

图1 计算模型(单位：m)Fig. 1 Numerical model

陈果[9]指出轨道在某种脉冲激扰源作用下引起的振动，大体可影响激振点前后10跨轨枕范围，超出该范围，振动传播极弱，可认为无影响。文中数值模型纵向尺寸为30 m，第一轮对激振点与最后轮对激振点至模型纵向边界的距离均为15跨轨枕。模型中心对称边界采取水平约束，地基侧面边界采用弹簧-阻尼模拟无限远，模型底部采用各向固定约束。为方便对计算结果进行分析，沿路基中心线设置监测点A0、A1、A2和A3，深度依次为0、1、2、3 m，在地基表面距路基中心线1.5 m处设置监测点B0。

1.2 材料本构模型及参数

对于高铁路基，若填料参数满足相关设计规范，则路基填筑部分的压缩变形量很小，路基沉降主要由地基压缩引起。因此，轨道板、基床表层、基床底层和路堤均采用弹性模型；地基土看作弹塑性模型，采用Mohr-Coulomb模型进行模拟，各部分建模参数见表 1。

表1 建模参数

1.3 列车荷载模拟

列车运行时，路基承受的动荷载主要来自于列车自重在不平顺轨道上形成的激振力，大量列车荷载监测结果表明路基中动荷载幅值为20～100 kPa。铁道部科学研究院对列车运行试验数据进行分析计算，提出了路基设计动应力幅值经验计算式[10]

σd=0.26×P×(1+αv)

(1)

式中：σd为路基设计动应力幅值，kPa；P为单节车厢静轴重，kN；v为列车速度；α为速度影响系数，高速和准高速铁路无缝线路分别取0.003和0.004；1+αv为冲击系数，最大冲击系数为1.9，即速度在300 km/h以内时，按式(1)计算，超过300 km/h时，按300 km/h计算。笔者参考该研究成果确定动荷载幅值。

根据大量高铁路基动荷载监测成果[11-12]，实际高铁列车运行时的动荷载波形如图 2，为方便数值模拟，对动荷载波形做如图 2所示的简化。

图 2 高速列车荷载简化示意Fig. 2 Simplified sketch of high-speed train load

从图 2可以看出，列车荷载简化波形的波长为列车车厢长L1和转向架长L2之和，我国CH2型动车组的L1一般为25 m，L2为2.5 m。因此，确定列车时速后可根据式(2)求得列车动荷载频率f。

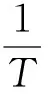
(2)

以我国CRH2A型动车组列车为例，单节车厢长25 m，转向架固定轴距2.5 m，车体轴重不超过14 t，一般约为12 t。列车时速为300 km/h时，按照式(2)确定的f和σd分别约为3.5 Hz和60 kPa。考虑实际条件下列车振动频率比简化后的频率高，对于一般工况，笔者取振动频率f为5 Hz，动应力幅值σd为60 kPa。

1.4 计算工况

式(1)表明高铁列车动荷载幅值与列车速度成正相关关系，列车速度越高，对应的列车荷载幅值也越大。笔者以列车速度的大小来表征动荷载幅值的大小，重点分析列车速度、路堤高度和不同基床刚度组合对地基动应力及长期沉降的影响，数值模拟工况见表2。

将每次列车经过视为一次加载过程，计算经过一定次数循环加载之后的地基沉降。已有研究成果表明：地基沉降随列车加载次数的增加呈幂函数增加，加载次数达一定程度时，沉降趋于稳定，笔者取沉降稳定值进行分析。

表2 数值模拟工况

2 数值模拟结果分析

2.1 地基动应力分布

列车运行引起的地基动应力分布是地基动力稳定性分析的关键，也是计算列车运行引起的地基长期沉降的基础。采用三维有限元可以得到地基沉降稳定时地基内部任意位置的6个动应力分量σxx、σyy、σzz、τxy、τxz、τyz的幅值，并据此计算得到mises应力σs。

图 3 地基动应力沿水平方向变化曲线Fig. 3 Variation curve of dynamic stress of foundation changing along the horizontal direction

图3为列车速度为40 m/s时地基动应力变化。随着距路基中心距离增大，σxx先小幅增加后逐渐减小，而σyy、σzz和σs均快速减小，距路基中心3 m时，σzz衰减幅度达90%，距路基中心7.5 m时，σxx和σzz均已接近于0。

图4为列车速度为40 m/s时路基中心线和距中心线1.5 m处σzz随深度的变化。σzz随深度增加不断减小，5 m深度内σzz迅速衰减，路基中心线5 m深度处的σzz与地表处相比，衰减幅度达50%；路基中心线处σzz随深度衰减速度是距路基中心线1.5 m处的1.5倍；地基深度7 m处，σzz均小于4 kPa。

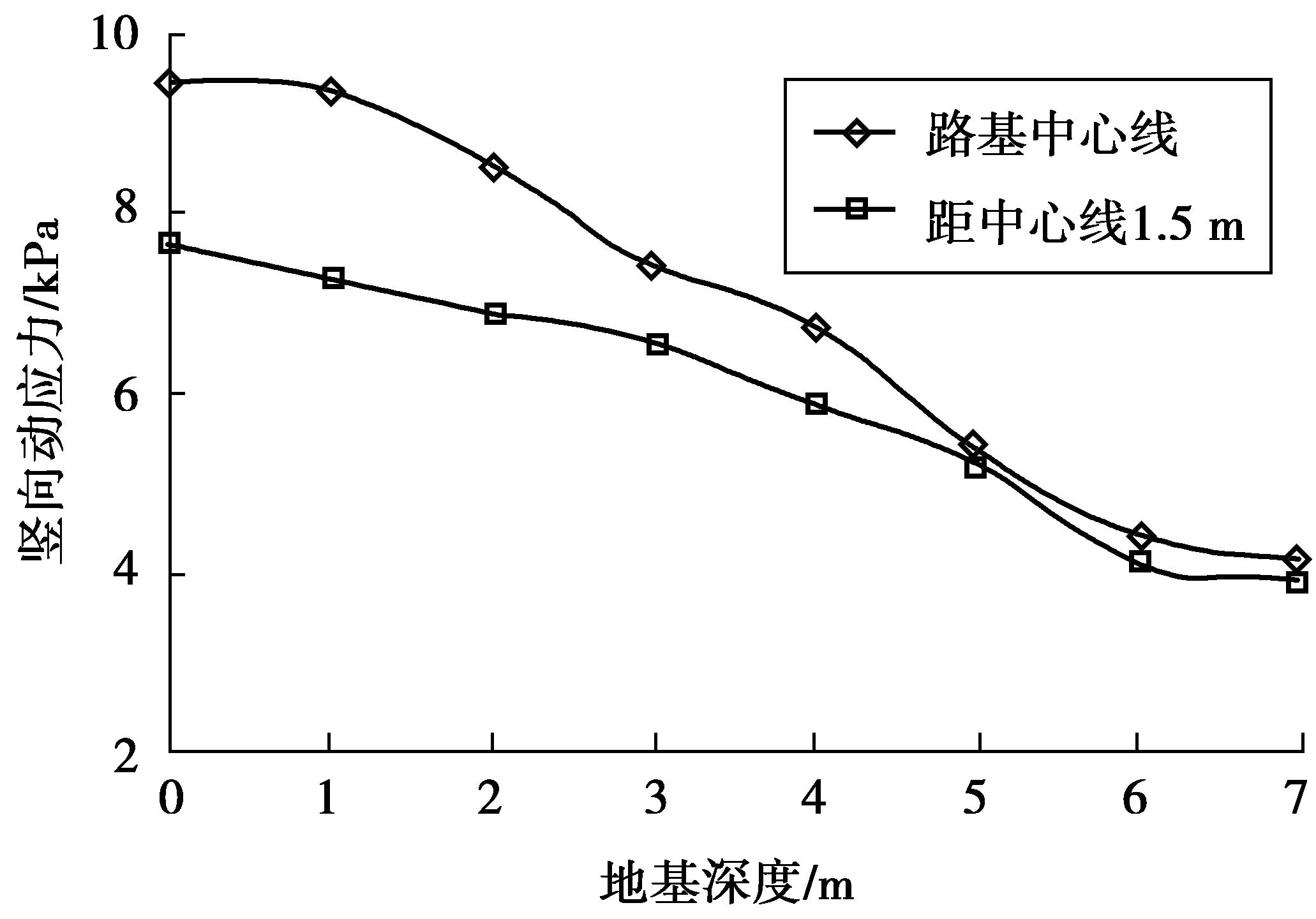
图4 地基竖向动应力随深度变化曲线Fig. 4 Variation curve of vertical dynamic stress of foundation changing with depth

2.2 列车速度的影响

图 5为列车速度对地基竖向动应力的影响。随列车速度增加，不同地基深度D处的σzz均不断增大；列车速度由40 m/s提高到60 m/s时，σzz增大速率较快，列车速度由60 m/s增大到100 m/s时，σzz增大速率较小；列车速度由40 m/s提高到60 m/s时，地基表面监测点A0的σzz提高了20%，而地基表面下3 m处监测点A3的σzz则提高了30%。

图6为列车速度对地基沉降的影响，取路基中心线处监测点A0和A1的沉降进行分析。随列车速度增加，地基沉降近似线性增长，监测点A0和A1的沉降趋势相近；列车速度由40 m/s提高到100 m/s时，监测点A0和A1的沉降均约增加了0.16 cm。

图5 列车速度对地基竖向动应力的影响Fig. 5 Effect of train speed on the vertical dynamic stress of foudation

图6 列车速度对地基沉降的影响Fig. 6 Effect of train speed on foudation settlement

2.3 路堤高度的影响

分别取路堤高度H为1、2和3 m 3种工况进行分析，列车速度取100 m/s。图 7为路堤高度对路基中心线处地基竖向动应力的影响。随路堤高度增加，σzz逐渐减小，不同路堤高度下σzz沿深度变化趋势相近；路堤高度由1 m增加到3 m，不同深度处σzz均降低了约20%；随地基深度增加，路堤高度对σzz的影响逐渐减小。

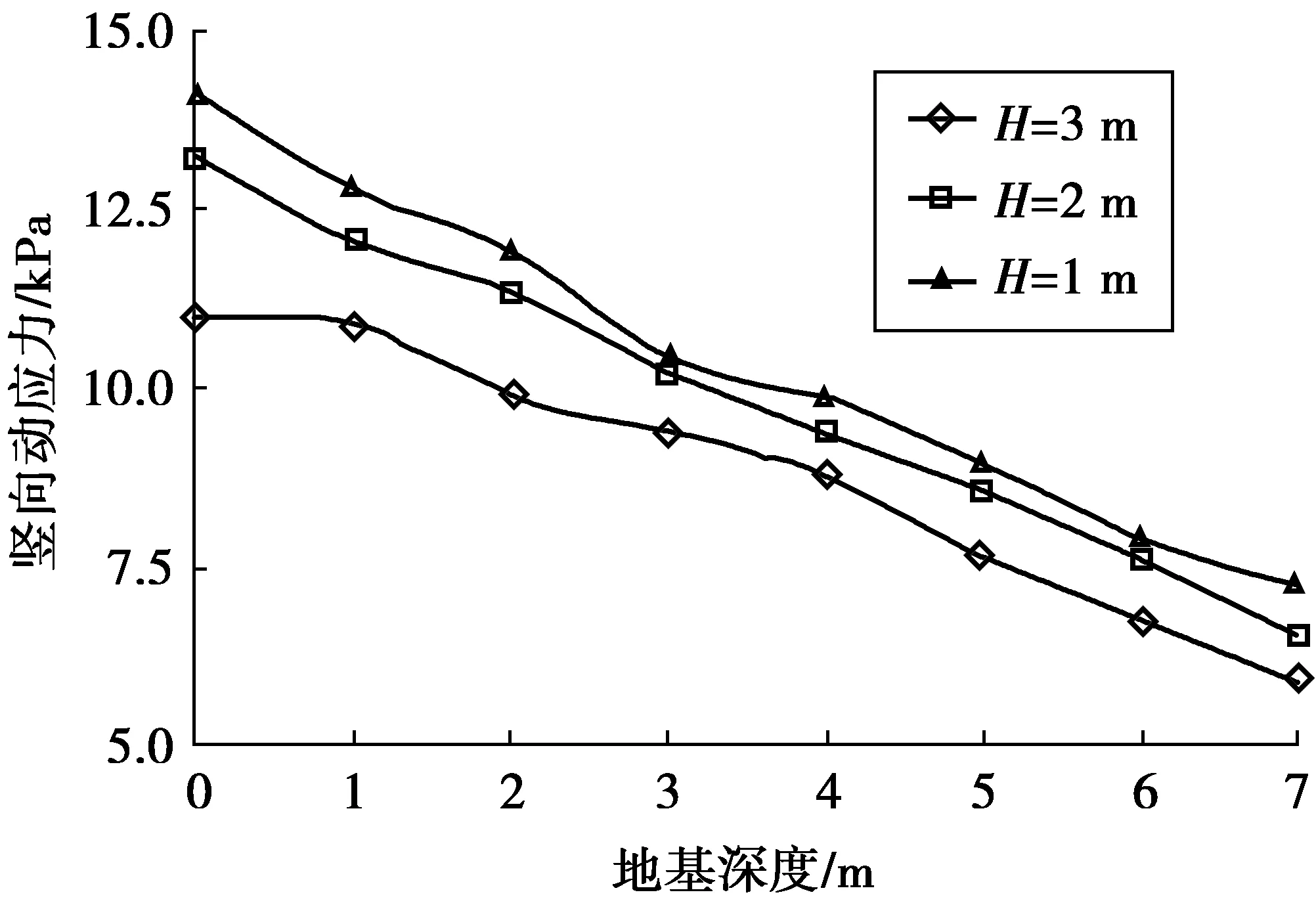
图7 路堤高度对地基竖向动应力的影响Fig. 7 Effect of embankment height on the vertical dynamic stress of foudation

图8为路堤高度对地基沉降的影响，取路基中心线处监测点A0和A1进行分析。随路堤高度增加，地基沉降近似线性减小；路堤高度由1 m增加到3 m时，监测点A0和A1的沉降均减小了约0.14 cm；对于不同高度的路堤，监测点A0和A1的沉降差值始终保持在0.15 cm左右。

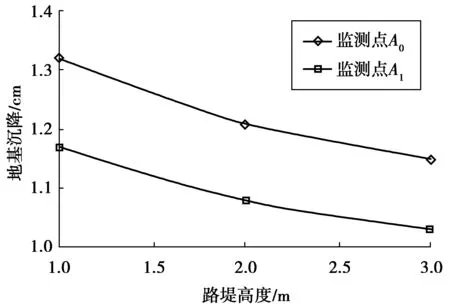
图8 路堤高度对地基沉降的影响Fig. 8 Effect of embankment height on the foudation settlement

2.4 基床刚度的影响

选取3种基床刚度组合工况，分别为组合①(100+40 MPa)、组合②(150+60 MPa)和组合③(200+80 MPa)，列车速度取100 m/s。图 9为基床刚度组合对路基中心线处地基竖向动应力的影响。随基床刚度增大，σzz明显降低，不同刚度组合下，σzz沿深度变化趋势相近；地基表面下不同深度处，基床刚度由组合①增大到组合③时，σzz均降低20%左右；随地基深度增加，基床刚度对σzz的影响逐渐降低。

图9 基床刚度对地基竖向动应力的影响Fig.9 Effect of base stiffness on the vertical dynamic stress of foudation

图10为基床刚度组合对路基中心线处地基沉降的影响。随基床刚度增大，相同深度处的地基沉降明显减小，组合③的沉降比组合①小0.2 cm；随地基深度增加，不同基床刚度组合下的沉降及沉降差值均逐渐减小；地基表面下3 m深度范围内沉降受基床刚度影响较为明显。列车动荷载引起的长期沉降主要存在于地基浅层。

图10 基床刚度对地基沉降的影响Fig. 10 Effect of base stiffness on foudation settlement

4 地基加固效果分析

为降低列车荷载作用下的地基沉降，需对不良地基进行处理。本节采用弹性加固区对地基进行改良，分析加固区深度和刚度对地基沉降的影响。

图11为地基加固示意图，加固宽度B=30 m，加固深度D=0～5 m。为研究加固区刚度的影响，分别取加固区刚度为20、40和60 MPa，分析对应工况下的地基沉降。

图11 地基加固示意(单位：m)Fig. 11 Sketch of foundation reinforecment

图12为加固深度对地基沉降的影响，取路基中心线处监测点A0和A1的沉降进行分析，加固区刚度取20 MPa。列车速度为60 m/s时，随加固深度增加，监测点A0和A1的沉降均逐渐减小，且减小速率逐渐降低，加固深度达3 m时，增大加固深度对降低沉降的效果不明显；列车速度为100 m/s且加固深度不大于3 m时，监测点A0和A1的沉降随加固深度的增大明显降低，加固深度超过3 m时，继续增大加固深度对降低地基沉降的影响不大。

图12 加固深度对地基沉降的影响Fig. 12 Effect of reinforcement depth on foudation settlement

图13 加固区刚度对地基沉降的影响Fig. 13 Effect of stiffness of the reinforeced area on foundation settlement

图13为加固区刚度对地基沉降的影响。不同列车速度下，随加固区刚度增加，地基沉降均明显降低，加固区刚度达60 MPa时，继续提高加固区刚度对于降低地基沉降的效果不明显；列车速度为100 m/s时，加固区刚度对地基沉降的影响较列车速度为60 m/s时更显著。

5 结 论

1)列车荷载作用下，地基内部动应力沿地基深度迅速减小，目前实际运营动车组的动应力对地基的影响主要集中在5 m深度内。

2)地基竖向动应力和沉降随列车速度增大而增大，随路堤高度和基床刚度增大而减小，总体而言，路堤高度对地基竖向动应力影响较大，而基床刚度对地基沉降影响较大。为减小列车荷载对地基的影响，路堤高度不宜小于2 m。

3)列车荷载作用下，地基沉降随加固深度和加固区刚度增大而减小，列车速度越高，影响越明显，最佳地基加固深度为3 m。

[1] 王常晶,陈云敏. 列车荷载在地基中引起的应力响应分析[J].岩石力学与工程学报,2005, 24(7): 1178-1186. WANG Changjing, CHEN Yunmin. Analysis of stresses in train-induced ground[J].ChineseJournalofRockMechanicsandEngineering, 2005, 24(7): 1178-1186.

[2] 陈建国, 肖军华, 李前进, 等. 提速列车荷载作用下铁路路基动力特性的研究[J]. 岩土力学, 2009, 30(7): 1944-1950. CHEN Jianguo,XIAO Junhua,LI Qianjin,et al. Dynamic responses of existing-railway subgrade with train speed increasing[J].RockandSoilMechanics, 2009, 30(7): 1944-1950.

[3] EKEVID T, WIBERG N E. Wave propagation related to high-speed train: A scaled boundary FE-approach for unbounded domains[J].ComputerMethodsinAppliedMechanicsandEngineering, 2002, 191(36): 3947-3964.

[4] PAOLUCCI R, MAFFEIS A, SCANDELLA L, et al. Numerical prediction of low-frequency ground vibrations induced by high-speed trains at Ledsgaard, Sweden[J].SoilDynamicsandEarthquakeEngineering, 2003, 23(6): 425-433.

[5] 蔡英，曹新文. 重复加载下路基填土的临界动应力和永久变形初探[J]. 西南交通大学学报, 1996, 31(1): 1-5. CAI Ying, CAO Xinwen. Study of the critical dynamic stress and permanent strain of the subgrade-soil under the repeated load [J].JournalofSouthwestJiaotongUniversity, 1996, 31(1): 1-5.

[6] 董亮, 蔡德钩, 叶阳升, 等. 列车循环荷载作用下高速铁路路基累积变形预测方法[J]. 土木工程学报, 2010, 43(6): 100-108. DONG Liang, CAI Degou, YE Yangsheng, et al. A method for edicting the cumulative deformation of high-speed railway subgrades under cyclic train loads[J].ChinaCivilEngineeringJournal, 2010, 43(6): 100-108.

[7] 肖军华, 周顺华, 韦凯. 列车振动荷载下铁路粉土路基的长期沉降[J]. 浙江大学学报(工学版), 2010, 44(10): 1912-1918. XIAO Junhua, ZHOU Shunhua, WEI Kai. Long term settlement of railroad silt subgrade induced by train loading[J].JournalofZhejiangUniversity(EngineeringScience),2010,44(10):1912-1918.

[8] 中华人民共和国铁道部. 高速铁路设计规范：TB10621—2014[S].北京:中国铁道出版社, 2014. National Railway Administration of the People’s Republic of China.CodeofDesignforHigh-SpeedRailway:TB10621—2014[S].Beijing: China Railway Publishing House, 2014.

[9] 陈果. 车辆-轨道耦合系统随机振动分析[D].成都: 西南交通大学, 2001. CHEN Guo.TheAnalysisonRandomVibrationofVehicle/TrackCouplingSystem[D].Chengdu:Southwest Jiaotong University, 2001.

[10] 李向国.高速铁路技术[M].北京:中国铁道出版社, 2005:35-38. LI Xiangguo.High-SpeedRailwayTechnology[M]. Beijing: China Railway Publishing House, 2005: 35-38.

[11] 刘晓红. 高速铁路无砟轨道红黏土路基动力稳定性研究[D].长沙: 中南大学, 2011. LIU Xiaohong.ResearchonDynamicStabilityofRedClaySubgradeunderBallastlessTrackofHigh-SpeedRailway[D].Changsha: Central South University, 2011.

[12] 吉林. 列车荷载作用下复合地基沉降特性研究[D].北京:北京交通大学, 2011. JI Lin.StudyonSettlementCharactersofCompositeFoundationunderTrainLoad[D].Beijing:Beijing Jiaotong University, 2011.

(责任编辑：朱汉容)

DynamicStressandSettlementCharateristicsofFoundationunderTrainLoad

CHEN Jun

(Construction Management Office of Ji-He Expressway, Linfen 041699, Shanxi, P.R.China)

In order to analyze the dynamic stress and settlement charcteristics of the foudation under train load, the dynamic coupling numerical model of rail-embankment-foudation interaction under train load was established, considering the effect of train speed, embankment height and base stiffness. The dynamic stress distribution of the foudation and settlement charcteristics of surface under train load were researched, and the reinforcement effect of different foundation reinforcement forms was discussed. The results show that the dynamic stress of foundation decreases quickly along the horizontal and vertical direction under train load. The vertical dynamic stress of foundation and foundation settlement increase as the train speed increases, while decrease with the increase of the embankment height and base stiffness. The embankment height should not be less than 2 m. The foudation settlement decreases with the increase of the reinforcement depth and stiffness of the reinforced area. The higher train speed, the more obvious effect; and the best foundation reinforcement depth is 3 m.

railway engineering; train load; numerical simulation; dynamic stress of foundation; foundation settlement; foundation reinforcement

U231.1

：A

：1674- 0696(2017)09- 032- 06

10.3969/j.issn.1674-0696.2017.09.07

2016-04-19；

：2016-06-20

陈 俊(1967—)，男，山西襄汾人，高级工程师，主要研究方向为道路工程。E-mail:sxjt_jgc@126.com。