钢箱梁角焊缝表面裂纹应力特征及影响因素分析

吉伯海，谢曙辉，傅中秋，姚 悦

(河海大学 土木与交通学院，江苏 南京 210098)

钢箱梁角焊缝表面裂纹应力特征及影响因素分析

吉伯海，谢曙辉，傅中秋，姚 悦

(河海大学 土木与交通学院，江苏 南京 210098)

结合钢箱梁局部模型试件，针对角焊缝表面裂纹进行数值模拟，进行了裂纹尖端与裂纹前缘应力分布分析，并基于最大切向应力准则计算了裂纹面参考点的应力强度因子，最后结合疲劳裂纹实际扩展变化，考虑了不同裂纹形状对应力和应力强度因子的影响。分析结果表明：裂纹尖端存在严重的应力集中，裂纹区应力下降明显，裂纹前缘的应力水平与未出现裂纹时相同位置截面上表面应力水平相当；裂纹面受拉压应力，II型和III型应力强度因子基本为0，I型应力强度因子总体上随着参考点角度的增大而逐渐减小；裂纹尖端应力与裂纹短长轴比基本呈线性增大关系，在短长轴比0.6以后增速减缓，随着短长轴比的增大，裂纹深度方向前缘处应力强度因子变化幅度较裂纹尖端处更大，与长裂纹区相比，短裂纹区这种差异性较明显。

桥梁工程；疲劳；表面裂纹；应力；应力强度因子

0 引 言

正交异性钢桥面板结构自重轻，承载能力强，因而在大跨度桥梁中广泛使用[1]。根据实际工程应用，钢桥构件之间的连接焊缝大致分为角焊缝和对接焊缝两种。由于桥面板直接承受重车往复作用，加之正交异性桥面板肋间传力复杂，应力集中现象明显，不可避免会产生疲劳裂纹[2]，据日本土木学会钢构造委员会2007年对东京高速公路和阪神高速公路的钢桥面板疲劳裂纹的统计，纵肋与顶板、纵肋与横隔板连接的角焊缝处疲劳裂纹占总疲劳裂纹的主要地位[3]。裂纹可分为边裂纹、穿透裂纹、内埋裂纹和表面裂纹[4]，角焊缝处疲劳裂纹大多为表面裂纹[5]。

焊缝处裂纹在深度上的变化往往难以察觉，国内学者在裂纹检测方面做了相关研究[6]。目前除了钢桥连接焊缝的疲劳寿命分析[7]以外，疲劳裂纹的有限元分析也值得关注。对于裂纹的有限元分析，不可避免涉及到尖端应力奇异性，通过将单元中心节点移至四分之一处的1/4节点法对边裂纹分析简便易行[8]，而对表面裂纹及内埋裂纹的裂纹面曲线前缘来说处理相对困难，往往要自编程序才能实现[9]。美国西北大学T.BELYTSCHKO教授为代表的研究组，于1999年首先提出来的扩展有限元法[10]，是求解不连续力学问题最有效的一种数值方法。国内外学者利用有限元方法在裂纹扩展模拟[11-12]、应力强度因子计算[13-14]等方面做大量工作，但研究分析大多以紧凑拉伸试件以及中央单裂纹试件为对象，而结合钢桥疲劳裂纹的实际情况进行应用分析的还较少。笔者利用ABAQUS扩展有限元技术对角焊缝处表面裂纹进行应力特征分析、应力强度因子计算，最后结合裂纹扩展过程中形状的变化对应力和应力强度因子的影响进行了探讨。

1 应力特征分析

1.1 分析模型

根据钢箱梁局部模型试件进行有限元模拟分析。模型参数：顶板长600 mm，宽300 mm，厚16 mm，U肋厚8 mm。Q345qD钢材材料参数：弹性模量E=206 GPa，泊松比υ=0.3。荷载情况：共计4个加载面，荷载集度为0.53 MPa，使得模型在未设置裂纹时，距焊趾10 mm截面上表面中心位置处的拉应力大小为50 MPa。边界条件：顶板U肋锐角侧，距边缘230 mm范围内全自由度约束。

图1 模型尺寸(单位：mm)Fig. 1 Model size

考虑到实际裂纹并不是恰巧产生在焊趾处，故模拟裂纹位置位于距焊趾0.5 mm处。裂纹类型为表面裂纹，裂纹几何参数为：半长轴a=50 mm，半短轴b=10 mm，即短长轴比为0.2。长轴端点为裂纹尖端，两点之间的曲线段为裂纹前缘，对于裂纹面应力及应力强度因子的比较，选取半椭圆长轴左侧为0°方向，逆时针方向标示角度，具体参考点如图2。

图2 表面裂纹示意Fig. 2 Sketch of surface crack

采用ABAQUS 6.13-1进行建模分析，利用扩展有限元技术处理裂纹尖端应力奇异性问题。采用C3D8R八节点线性缩减积分六面体单元以及C3D10十节点二次四面体单元进行网格混合划分，整体网格划分及局部网格加密如图3。

图3 有限元模型Fig. 3 Finite element model

1.2 裂纹尖端应力分析

通过有限元计算，得到裂纹尖端附近应力云图如图4。

图4 裂纹尖端应力云图Fig. 4 Stress contour of crack tip

从应力云图上可以看出，由于裂纹的存在，引起了截面应力分布严重不平衡，裂纹区间几乎不存在应力，而在裂纹尖端存在明显的应力集中现象，且存在类似四分之一圆的应力辐射区。

进行裂纹设置前后的模型应力对比分析，提取距焊趾0.5 mm，平行于焊趾方向的Mises等效应力，即表面裂纹截面处，顶板上表面路径上的应力，绘制应力分布图如图5。

需要说明的是，ABAQUS提供两种应力结果插值计算方式，分别是compute scalars before average和compute scalars after average。理论上，在模型网格划分较好的情况下，前一种情形设置阈值为100%时插值得到的计算结果，与后一种情形的插值方法计算出的结果应该接近。可以看出，本次计算中，两者结果符合较好，为表达简洁，接下来的应力分析选取其一进行讨论。

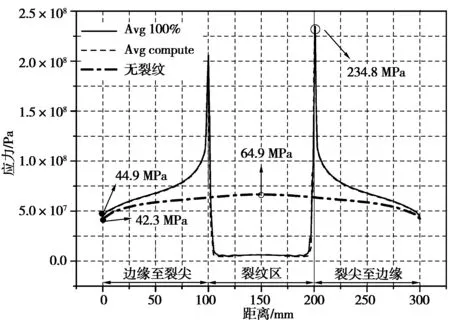
图5 Mises应力分布Fig. 5 Mises stress distribution

从图5可以看出，模型未设置裂纹时，最大应力位置出现在截面中央为64.9 MPa，截面边缘应力为42.3 MPa，考虑到加载位置的影响，截面应力分布曲线呈半椭圆形，总的来说构件的整体应力分布均匀。

但是，当模型设置100 mm长的表面裂纹后，从截面边缘至裂纹尖端方向上，应力急剧上升，两个裂纹尖端位置之间应力大幅下降，在裂纹尖端位置出现明显的应力集中现象。

经计算，裂纹区的平均应力值为12.1 MPa，与未设置裂纹模型相比，相同区间的平均应力为64.6 MPa，下降了81.3%。构件边缘应力略有升高，为44.9 MPa，而裂尖应力值达到了234.8 MPa，裂纹尖端至截面边缘之间的应力有不同幅度的提高。

在材料的弹性范围内，反映局部应力增高程度的参数称为应力集中系数Kt，它是局部峰值应力与名义应力的比值。据此，可以计算出本模型裂尖处的应力集中系数Kt。

式中：σmax为局部峰值应力；σnom为名义应力。

由此可以看出，当构件出现裂纹后，截面应力发生重新分布，裂纹区几乎不参与截面受力，而裂纹尖端应力急剧增大，适当情况下会达到材料的屈服强度。因此，在实际工程中，当构件出现裂纹后，应重视对裂纹尖端应力集中的处理。

1.3 裂纹前缘应力分析

通过有限元计算，得到裂纹前缘附近应力云图如图6。

图6 裂纹前缘应力云图Fig. 6 Stress contour of crack front

从应力云图上可以看出，在远端弯矩的作用下，构件截面上下侧均出现较大的应力，在裂纹前缘也存在较大的应力，裂纹尖端应力集中现象明显，且在裂纹尖端附近，存在一定范围的应力辐射区。

由于裂纹面对称，分别提取裂纹面0°～90°位置处截面深度方向上的应力，绘制深度方向上应力分布图如图7。

从图7可以看出，在裂纹面0°方向上，即裂纹尖端处，应力随着深度的增大呈先增大后减小、再增大的趋势，这是由于截面在弯矩作用下，构件上下表面存在较大应力，而截面中性轴附近应力较小，加之上表面存在裂纹尖端，即应力集中点，故上表面相对下表面来说应力很大。

在裂纹面的其余方向上，构件在外力作用下，裂纹面分离，导致上表面的应力往裂纹区两侧分布，故裂纹区上表面的应力都很小，在深度方向上，应力值总体呈上升趋势，其中，各角度在深度方向上，在裂纹前缘处出现一个明显的应力高峰，峰值应力处在50～75 MPa区间内，应力水平与未设置裂纹时构件截面上表面应力水平相当。峰值过后，应力先减小后增大，可以看作裂纹区受力面减小，截面中性轴下移。另外可以发现，除了裂纹尖端，其余各角度上应力存在一个共性，即深度方向上的应力最大值出现在下表面。

1.4 应力强度因子计算

应力强度因子是反映裂纹尖端弹性应力场强弱变化的物理量。

根据断裂力学理论，依据裂纹前缘邻域的变形状态，有如图8所示的3种裂纹类型。这3种类型裂纹分别称作张开型裂纹、滑开型裂纹、撕开型裂纹。根据其相应变形状态计算出的应力强度因子分别为KI、KII、KIII。在单向应力作用下的裂纹，称为纯裂纹，其他各种状况下都称为复合型裂纹。

根据本次计算模型中裂纹面对称，故提取0°～90°方向上各点来计算表面裂纹尖端不同角度上的应力强度因子，绘制应力强度因子随裂纹面参考点角度变化的趋势图如图9。

另外可以看出，KII和KIII在各个角度上值都在0附近，考虑到构件模型在远端承受压应力作用，裂纹面承受弯矩，截面上下两侧以拉压应力为主，II、III类型的应力强度因子大小基本为0，因此接下的裂纹形状影响分析以I型应力强度因子分析为主。

2 裂纹形状的影响

2.1 短裂纹

结合疲劳裂纹在萌生阶段首先以深度方向扩展为主的特点。在半长轴a=15 mm情况下，考虑不同短长轴比b/a对裂纹尖端应力以及I型应力强度因子的影响。为了直观地表明各工况下短裂纹的变化，绘制裂纹面的分析示意如图10。

为了明显地比较裂纹面应力及应力强度因子随着裂纹形状变化的规律，将上述各工况的裂纹尖端应力以及裂纹面各角度I型应力强度因子汇总，绘制变化趋势图如图11、图12。

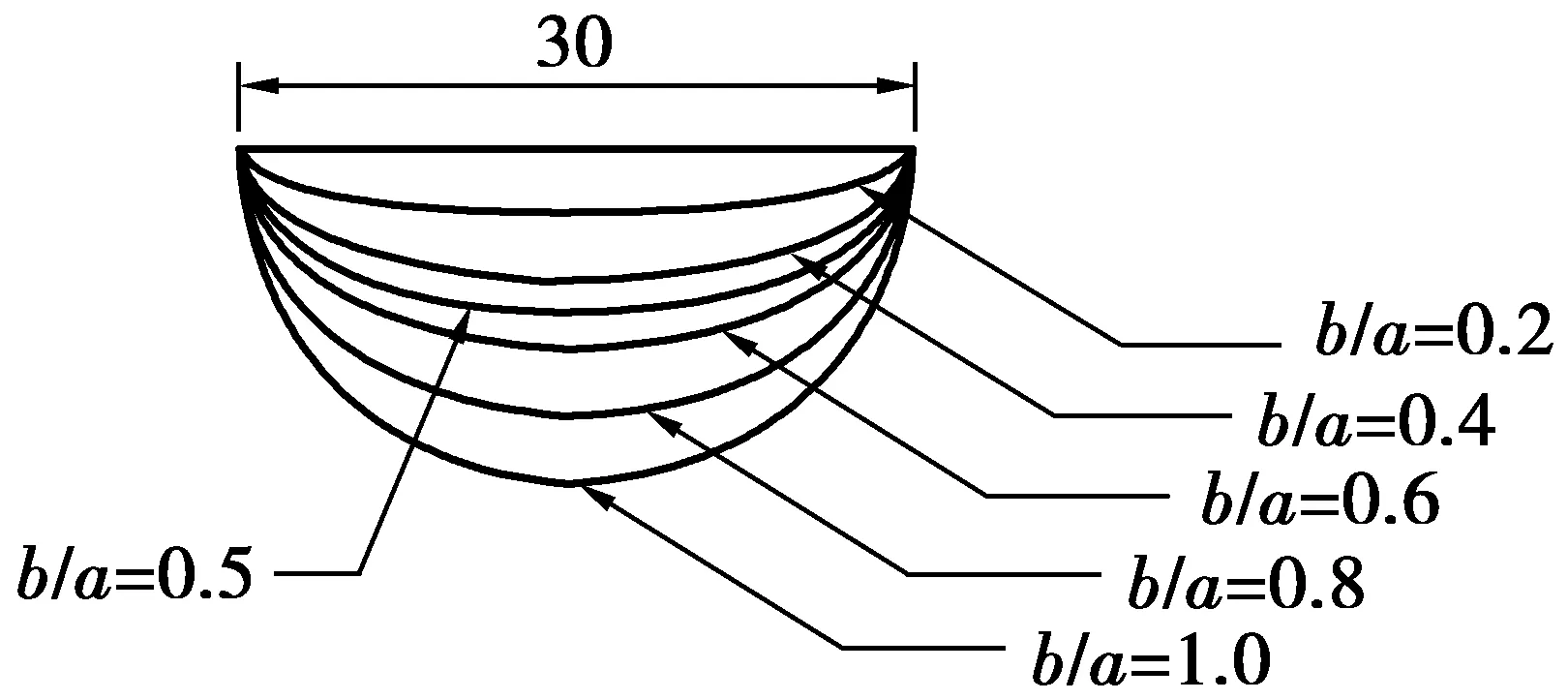
图10 短裂纹分析示意Fig. 10 Sketch of short cracks

图11 短裂纹裂纹尖端应力随裂纹形状变化趋势Fig. 11 Variation trend chart of crack tip stress of short crack changing with crack shape

图12 短裂纹I型应力强度因子随裂纹形状变化趋势Fig. 12 Variation trend chart of I type SIF of short crack changing with crack shape

从图11可以看出，在短裂纹区，随着裂纹面b/a值逐渐增大，裂纹尖端应力也随之逐渐增大，但在b/a=0.6以后，应力增幅速度有所放缓。

2.2 长裂纹

结合疲劳裂纹萌生到一定长度后，也会在深度方向继续扩展的特点。在半长轴a=50 mm情况下，考虑不同短长轴比b/a对裂纹尖端应力以及I型应力强度因子的影响。同样，为了直观地表明各工况下长裂纹的变化，绘制裂纹面的相关示意图如图13。

图13 长裂纹分析示意Fig. 13 Sketch of long cracks

为了明显地比较裂纹面应力及应力强度因子随着裂纹形状变化的规律，将上述各工况的裂纹尖端应力以及裂纹面各角度I型应力强度因子汇总，绘制变化趋势图如图14、图15。

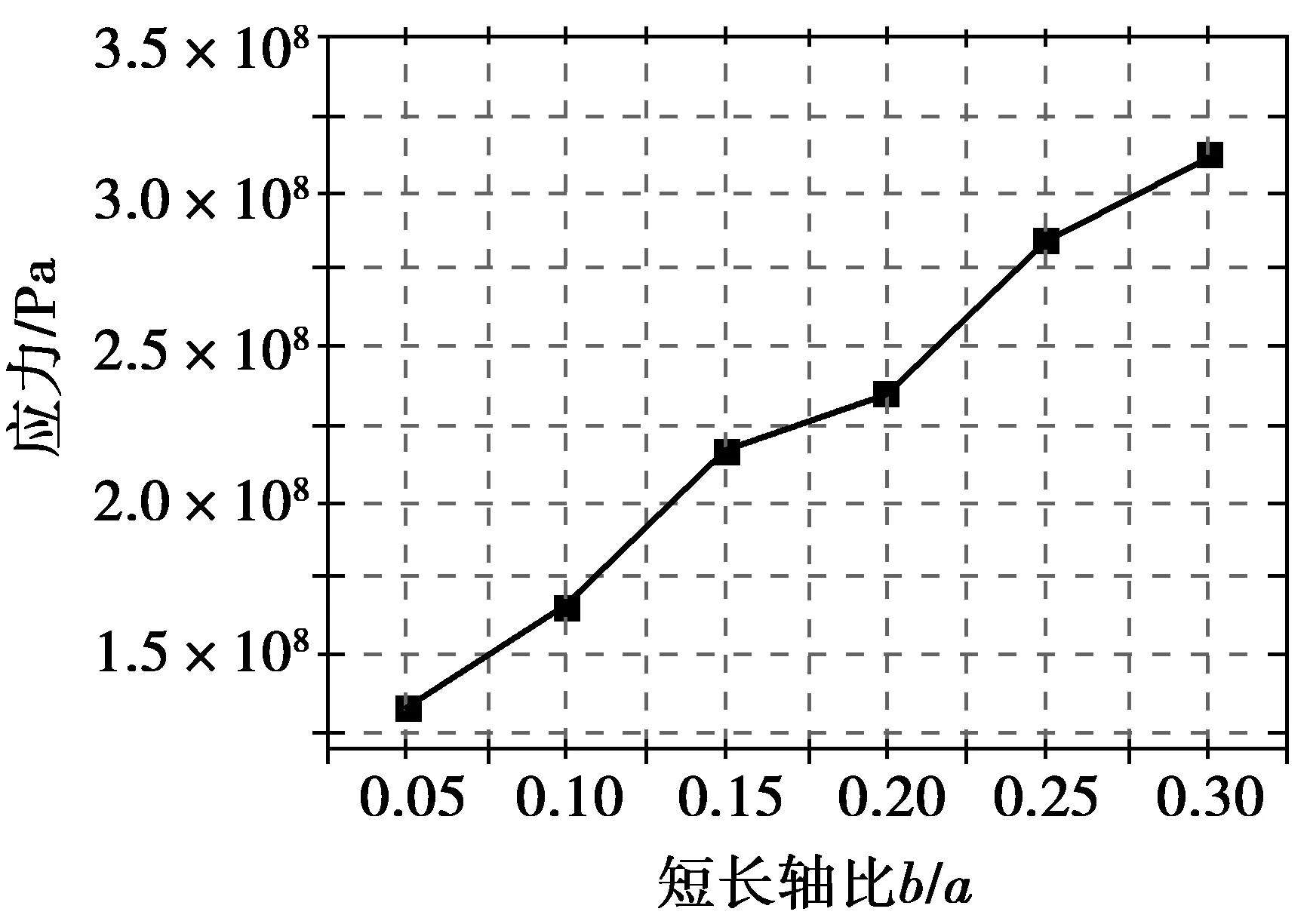
图14 长裂纹裂纹尖端应力随裂纹形状变化趋势Fig. 14 Variation trend of crack tip stress of long crack changing with crack shape

图15 长裂纹I型应力强度因子随裂纹形状变化趋势Fig. 15 Variation trend of I type SIF of long crack changing with crack shape

从图14可以看出，在长裂纹区，随着裂纹面b/a值逐渐增大，裂纹尖端应力也随之逐渐增大，裂纹尖端应力值与裂纹面b/a值总体上呈线性增大关系。

3 结 论

1)构件出现裂纹，引起截面应力重分布，在裂纹尖端出现严重的应力集中现象，裂纹区应力下降明显，裂纹前缘的应力水平与未出现裂纹时相同位置截面上表面应力水平相当。裂纹面深度方向上，在裂纹前缘处应力出现峰值，应力最大值出现在截面下表面。

2)在远端弯矩作用下，构件截面承受拉压应力，裂纹面曲线前缘上II型和III型应力强度因子基本为0，I型应力强度因子总体上呈现随裂纹面参考点角度增大而逐渐减小的趋势。

3)裂纹尖端应力与裂纹短长轴比基本呈线性增大关系，在短长轴比0.6以后增速减缓；随着裂纹短长轴比的逐渐增大，裂纹深度方向前缘处应力强度因子变化幅度较裂纹尖端更大，与长裂纹区相比，短裂纹区这种差异性较明显。

[1] 张陕锋. 正交异性板扁平钢箱梁若干问题研究[D].南京：东南大学, 2006. ZHANG Shanfeng.StructureCharacteristicsResearchofOrthotropicDeckFlatSteelBoxGirders[D].Nanjing:Southeast University, 2006.

[2] 曾志斌. 正交异性钢桥面板典型疲劳裂纹分类及其原因分析[J]. 钢结构, 2011, 26(2):9-15. ZENG Zhibin. Classification and reasons of typical fatigue cracks in orthotropic steel deck [J].SteelConstruction, 2011, 26(2): 9-15.

[3] 土木学会剛構造委員會. 厚板溶接継手に関する调査研究小委员会报告书[R].日本:[s.n.], 2007. Steel Structure Committee of Civil Society.ReportofThickPlateWeldingJointRelatedResearch[R].Japan:[s.n.], 2007.

[4] 张晓敏. 断裂力学[M].北京：清华大学出版社, 2012. ZHANG Xiaomin.FractureMechanics[M].Beijing:Tsinghua University Press, 2012.

[5] 成建国, 阿布雷克. 不同超载条件下带有角焊缝钢焊件的疲劳裂纹扩展速率[J]. 南京工业大学学报(自然科学版), 1983,5(2):10-19. CHENG Jiangguo, Albrecht. Fatigue crack growth rate of steel weld under overload conditions[J].JournalofNanjingTechnologyUniversity(NaturalScience), 1983, 5(2): 10-19.

[6] 袁周致远, 吉伯海, 傅中秋,等. 基于电阻法的钢桥疲劳裂纹检测方法研究[J]. 重庆交通大学学报(自然科学版), 2014,33(3):27-31. YUANZHOU Zhiyuan, JI Bohai, FU Zhongqiu, et al. Deck fatigue crack detection based on electrical resistance method [J].JournalofChongqingJiaotongUniversity(NaturalScience), 2014, 33(3): 27-31.

[7] 吉伯海, 朱伟, 傅中秋,等. 正交异性钢桥面板U肋对接焊缝疲劳寿命评估[J]. 重庆交通大学学报(自然科学版), 2015,34(1):16-21. JI Bohai, ZHU Wei, FU Zhongqiu, et al. Fatigue life evaluation of U-rib butt weld of the orthotropic steel bridge[J].JournalofChongqingJiaotongUniversity(NaturalScience),2015, 34(1): 16-21.

[8] 王永伟, 林哲. 表面裂纹的三维模拟及应力强度因子计算[J]. 中国海洋平台, 2006, 21(3):23-26. WANG Yongwei, LIN Zhe. 3D simulation and stress intensity factors [J].ChinaOffshorePlatform, 2006, 21(3): 23-26.

[9] 于培师. 含曲线裂纹结构的三维断裂与疲劳裂纹扩展模拟研究[D]. 南京：南京航空航天大学, 2010. YU Peishi.StudiesonThree-DimensionalFractureandFatigueCrackGrowthSimulationofCurveCrackedStructures[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2010.

[10] BELYTSCHKO T, BLACK T. Elastic crack growth in finite elements with minimal remeshing[J].InternationalJournalforNumericalMethodsinEngineering, 1999, 45(5): 601-620.

[11] 徐杰. 表面疲劳裂纹扩展的数值模拟[D]. 杭州：浙江理工大学, 2012. XU Jie.NumericalSimulationofFatigueCrackGrowthofSurfaceCrack[D]. Hangzhou: Zhejiang Sci-Tech University, 2012.

[12] NASRI K, ABBADI M, ZENASNI M, et al. Double crack growth analysis in the presence of a bi-material interface using XFEM and FEM modeling[J].EngineeringFractureMechanics, 2014, 132: 189-199.

[13] JIANG S, DU C, GU C, et al. XFEM analysis of the effects of voids, inclusions and other cracks on the dynamic stress intensity factor of a major crack[J].Fatigue&FractureofEngineeringMaterials&Structures, 2014, 37(8): 866-882.

[14] 彭志刚, 赵小兵, 刘青峰,等. 半椭圆表面裂纹前缘应力强度因子的计算[J]. 计算机仿真, 2008, 25(7):332-335. PENG Zhigang, ZHAO Xiaobing, LIU Qingfeng, et al. Calculation of stress intensity factor of semi-elliptical surface crack front[J].ComputerSimulation, 2008, 25(7): 332-335.

(责任编辑：朱汉容)

StressCharacteristicsandInfluenceFactorsofSurfaceCracknearFilletWeldinSteelBoxGirder

JI Bohai, XIE Shuhui, FU Zhongqiu, YAO Yue

(School of Civil and Transportation Engineering, Hohai University, Nanjing 210098, Jiangsu, P.R.China)

Based on specimen of steel girder bridge local model, the numerical simulation of fillet weld surface crack was carried out. Stress distribution of crack tip and front was analyzed, and stress intensity factor of reference point was calculated based on maximum tangential stress criterion. Additionally, according to actual fatigue crack shape change during propagation, the influence of different crack shapes on stress and stress intensity factor was considered. Analysis results indicate that crack tip appears severe stress concentration phenomena and stress of crack zone decreases obviously. Stress level of crack front is closed to that of cross-section at the same location surface without crack. Under tensile stress, stress intensity factor of type II and type III is approximately equal to zero; and KIdecreases gradually with the increase of angles of surface reference points on the whole. Crack tip stress increases linearly with the ratio of minor axis to major axis, and the growth rate slows down when the ratio is larger than 0.6. With the increase of the ratio of minor axis to major axis, the change range of stress intensity factor at front along crack depth is larger than that at crack tip, and comparing with long crack zone, this difference is more obvious in short crack zone.

bridge engineering; fatigue; surface crack; stress; stress intensity factor (SIF)

U448.36

：A

：1674- 0696(2017)09- 001- 05

10.3969/j.issn.1674-0696.2017.09.01

2016-03-30；

：2016-05-21

国家自然科学基金面上项目(51478163)；江苏省交通运输科技与成果转化项目(2017Y09)

吉伯海(1966—)，男，江苏扬州人，教授，博士，博士生导师，主要从事钢桥疲劳与维护方面的研究。E-mail：hhbhji@163.com。