基于Grey-Sigmoid核函数支持向量机高光谱遥感图像分类方法研究
王颢霖, 郭 伟, 师 越, 乔红波
(1.郑州外国语新枫杨学校,河南 郑州 450001; 2.河南农业大学信息与管理科学学院,河南 郑州 450002)
基于Grey-Sigmoid核函数支持向量机高光谱遥感图像分类方法研究
王颢霖1, 郭 伟2, 师 越2, 乔红波2
(1.郑州外国语新枫杨学校,河南 郑州 450001; 2.河南农业大学信息与管理科学学院,河南 郑州 450002)
针对传统支持向量机方法中存在的野值噪声敏感问题,提出了一种基于紧密度的Grey-Sigmoid核函数支持向量机,不仅考虑样本与所属类中心之间的关系,还考虑了各个样本之间的距离。通过样本之间的紧密度来描述各个样本之间的关系,利用包围同一类样本的最小超球半径来衡量样本间的紧密度,样本灰度依据样本在球中的位置确定。通过对田间小麦全蚀病的遥感图像分类的实验验证,证明Grey-Sigmoid核函数和传统的Sigmoid核函数相比,计算速度更快,且精度没有明显损失。
高光谱遥感;支持向量机;图像;分类
高光谱遥感信息具有数据量大、波段多、波段相关性强、信息冗余多、图谱一体化等特点,蕴含信息丰富,处理过程复杂,如何对其进行高效处理是遥感领域近年来研究的热点[1]。随着人工智能、机器学习、数据挖掘、高性能计算等相关学科技术的发展,遥感信息智能处理近年来已成为一个研究的热点[2]。智能处理有助于解决当前高光谱遥感信息处理中存在的诸如数据量大、处理过程复杂、速度慢、效率低、过多依赖于专家经验和人工参与等问题。支持向量机(Support Vector Machine,SVM)作为一种最新也是最有效的统计学习方法,近年来成为模式识别与机器学习领域一个新的研究热点。遥感图象分析与处理是SVM应用的一个热门研究方向,特别是在高光谱遥感分类中,SVM优越性得到了充分体现。SHAH等[3]试验发现SVM用于分类不需要降维,分类精度达到97%,不受Hughes现象的影响,能够很好地应用于高光谱分类中。NEMMOUR等[4]利用支持向量机技术研究郊区土地利用变化,和人工神经网络相比,支持向量机技术监测土地利用变化效果更好。在神经网络的应用中已经证明Sigmoid核函数具有良好的全局分类性[5-6],因此在支持向量机的研究中,使Sigmoid核函数更广泛的符合核函数的条件具有重要意义。由于Sigmoid核函数的非线性,软件实现起来比较困难且耗时较长。本研究提出一种基于灰色聚类的Sigmoid(以下简称Grey-Sigmoid)核函数,将灰色理论应用于核函数,简化计算且易于软件的实现。
1 材料与方法
1.1高光谱遥感图像获取
试验地点为河南省原阳县原武镇白沙村(35.029°N,113.819°E),供试小麦品种为郑麦366,利用12.5%全蚀净按1∶250、1∶500和1∶1 000 3个质量比梯度拌种,每梯度3个重复,小区面积30 m2,于2015年5月18日利用Headwall成像光谱仪测定其冠层的高光谱图像。Headwall成像光谱仪成像光谱范围为400~1 000 nm,光谱分辨率为5 nm,感光器件为CCD,瞬时视场角0.54 m rad,图像分辨率为1 392×1 024 pixels。测量时将Headwall成像光谱仪固定在Hyperspec®Pan & Tilt扫描云台上,成像光谱仪与地面夹角60°。测量前先进行白板校正,通过自带Hyperspec软件操作成像光谱仪进行数据采集与传输,在120 s内完成125幅窄波段光谱图像的连续采集,数据传输方式为USB 2.0,将采集到数据以BIL格式直接存储在便携式计算机内。
1.2构造基于紧密度的Grey-Sigmoid核函数
在支持向量机中,最优超平面通常由支持向量决定,而支持向量位于类边缘,常常伴随着野值和噪声。在确定样本的灰聚类时,如果无法有效地将样本与噪声进行正确的区分,计算出的超平面就不是最优的分类面[7-8]。因此,在Grey-Sigmoid核函数的构造中,灰色聚类的设计要求能够客观、准确的反应系统的不确定性。本研究提出一种基于紧密度的灰色聚类方法,在确定样本的聚类时,不仅考虑样本与样本中心之间的聚类,还考虑了样本间的紧密度,并在此基础上构造Grey-Sigmoid核函数。
1.2.1 样本集紧密度的确定 样本集的紧密度通过包围同类样本集的最小球半径来度量,通常,在样本数目不变的情况下,球半径越大紧密度越小[9]。当样本集中不存在噪声或野值时,只需寻找一个能包围所有同类样本的最小球半径;当样本集中含有噪声或野值样本时,可以允许小部分该类样本位于球外,此时,则寻找一个能够包围该类样本集中大多数样本的最小球半径。
设样本集x={x1,x2,…,xn},当样本集中不存在噪声或野值,或者事先不知道样本集中是否存在噪声或野值样本时,引入非负的松弛变量ζi(i=1,2,…,n),通过下面目标函数得到最小包围球:
(1)
式中:R为球半径,a为球中心,D>0为惩罚系数,D越大,对样本在球外的约束程度越大。
约束条件为:
‖xi-a‖2≤R2+ζi,i=1,2,…,n
(2)
ζi>0,i=1,2,…,n
(3)
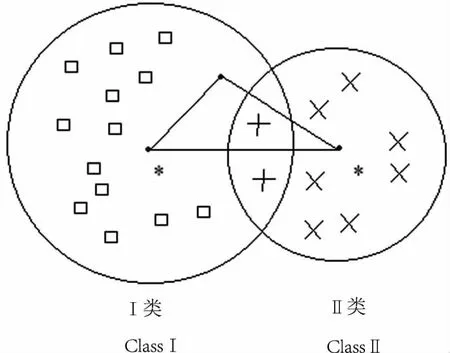
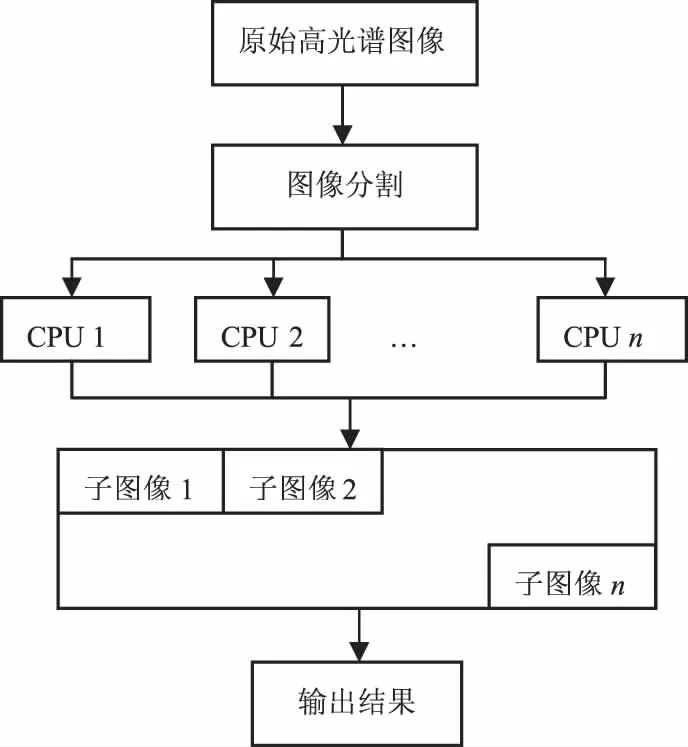
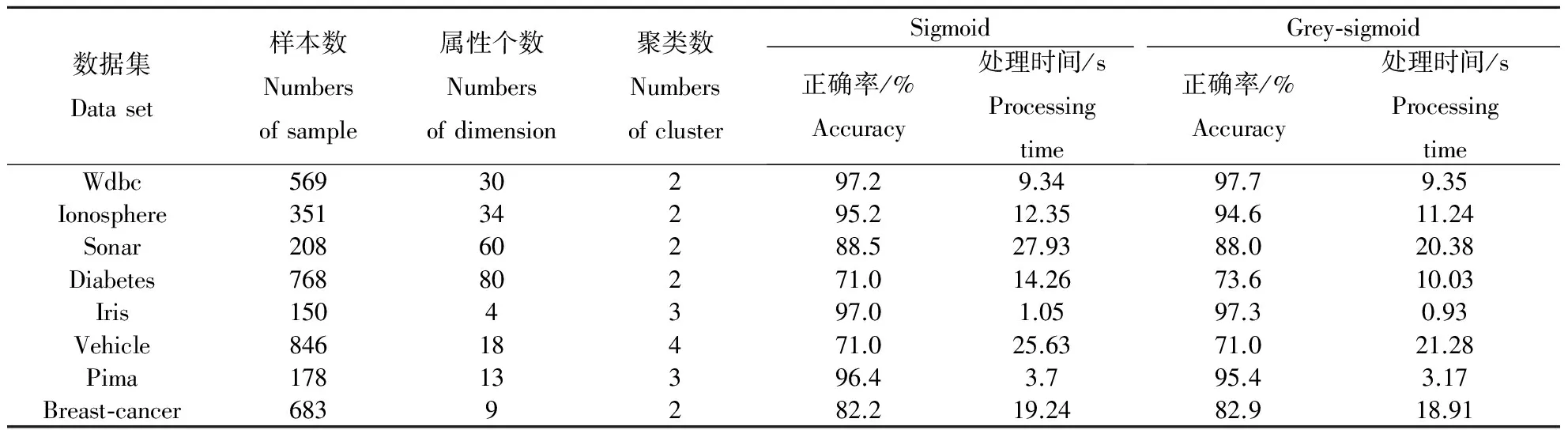
通过上述规划问题的求解,可以得到样本对应的Lagrange系数βi(i=1,2,…,n),当βi>0时,对应的是支持向量机的训练样本;当βi=D时,对应的样本位于包围球外边,称为野值或含噪声的样本。因此,最小的包围半径由0<βi R=‖x-a‖ (4) 式中:x为包围球在0<βi 1.2.2 基于紧密度的灰度计算 由于样本间紧密度是根据包围球半径来衡量,因此,在确定基于紧密度的灰度时,对分布在半径内、外的样本,采用两种不同的方式计算其灰度[10],设不同类别训练样本的数据序列Xi=(xi(1),xi(2)…xi(n)),令si为第i个类别序列的零化像,则: (5) 式中:R为同类样本最小包围球的半径;d(xi(1))为样本xi(1)到类中心的距离,根据公式(6)计算序列间的灰色绝对关联度。 (6) 取阀值r∈[0,1],一般要求r>0.6,当εij≥r(i≠j)时,则X1,Xj为同一聚类特征,r越大分类越细,r越小分类越粗。 1.3Grey集及Grey-Sigmoid核函数算法 首先引入Grey集概念:设论域x={x1,x2,…,xn}上的一个Grey集A由真灰度tA和假灰度fA描述,其中tA(xi)∈[0,1],是由支持xi的特征做导出的灰度下限,fA(xi) ∈[0,1]是由反对xi的特征做出的否定灰度下限,且tA(xi)+fA(xi)≤1,元素xi在Grey集A中被区间[0,1]的一个子集[tA(xi), 1-fA(xi)]界定,称该区间为xi在A中的Grey值,记为GA(xi)。 对于∀xi∈X,称hA(xi)=1-tA(xi)-fA(xi)为xi的Grey度,它描述了xi相对于Grey集A的踌躇度,是xi相对于A的不可知隶属度。 Grey-Sigmoid核函数算法描述: 1)将数据进行预处理,并分为训练样本集和测试样本集2类; 2)求训练样本的灰色聚类中心; 3)计算训练样本点的Grey值; 4)利用Grey-Sigmoid核函数,对带有Grey值得训练样本进行分类和测试。 1.4训练样本的Grey值 (7) 同理,如果属于Ⅱ类的情况,则定义: (8) (9) 1.5Grey集的相似度量及Grey-Sigmoid核 用2个样本点的相似度量代替欧氏距离:首先,计算对应的Grey值,然后表示成另一个空间的点,最后计算点间的相似度。 设样本xi和xj采用本文方法计算出的Grey值为G(xi)和G(xj),则它们在空间中对应的点Di表示为:Di(t(xi) (1+h(xi)),f(xi)(1+h(xi)),h2(xi));Dj(t(xj) (1+h(xj)),f(xj)(1+h(xj)),h2(xj)) 图1 类I中样本Grey值的计算Fig.1 Grey value computation of the sample in Class I 经以上定义的Di,Dj的相似度: (10) Grey-Sigmoid核函数: (11) 式中:γ=-r/a 1.6基于图像分块的并行处理框架 1.6.1 整体结构 对目标识别进行并行处理的核心是将原始光谱图像进行切割,将切割后的子图像分配到不同的处理器上同时进行处理,最后将所有的识别结果合并,得到最终的结果(图2)。 1.6.2 原始图像的切割 为保证分块后的子图像的识别结果与原图分类识别结果不变,要注意切割的方法。如果切割时将某个目标切割成多个子图像,则可能丢失此目标。本研究使用边界覆盖法来解决这个问题,即相邻的子图像之间有一定宽度的相互覆盖。为了尽可能快地提高计算速度,需要注意以下问题:1)子图像的大小要相同或比较接近,使得每台处理器的任务量相近; 2)子图像的长宽度最好相同,以保留更多的目标信息; 3)子图像的数量不宜过多,数量过多会导致目标信息的丢失,增大传输开销。 图2 并行处理框架图Fig.2 The parallel processing frame 2.1UCI数据集实验 为检验本文算法的鲁棒性和有效性,通过UCI选取8个数据集对算法进行验证[11]。在实验中将本文算法与传统Sigmoid核函数的支持向量机算法 进行对比。在1.5GHz,2G内存PC机上利用ENVI和Matlab 2004a实现算法运算。 从UCI中选取8个数据集分别为Wdbc、Ionosphere、Sonar、Diabetes、Iris、Vehicle、Pima和Breast-cancer,这8个数据是对比非监督分类的聚类效果和分类精度的典型数据,其基本特征和分类结果见表1。 支持向量机分类算法的性能很大程度上依赖于参数的优化选择。本文对sigmoid核函数及Grey-Sigmoid核函数的参数进行调优。在实验中存在2类参数:模型参数C(惩罚系数)和Sigmoid核参数a和r,其中参数惩罚系数C取100,a=1/n为固定值,n为输出样本的维数。参数r的选择用格搜索技术,参数r(r=[-4,…,0])被分成20个点。 为参数r选择一组候选值,然后计算参数对应的交叉验证的正确率。为了与Sigmoid核函数的支持向量机进行对比,我们使用10-fold交叉验证法。 从实验中发现,相对于传统的Sigmoid核函数,我们提出的Grey-Sigmoid核函数不仅在处理时间上有明显减少,而且在大多数数据集上分类精度也基本持平,甚至有所提高,但在Sonar,Ionosphere这样的高维数据集上,尽管处理时间有大幅减少,但本文提出的算法在处理效果上优势还不是很明显。 表1 数据集的基本信息及实验结果Table 1 Basic information of data set and results 2.2小麦全蚀病的高光谱图像分类应用实例 高光谱图像具有数据量大和运算复杂性高的特点。而基于sigmoid核函数的SVM算法在处理高光谱图像分类问题的时候,由于其解不具有稀疏性,所以测试和训练的时间比较长,无法满足田间小麦全蚀病高光谱图像的实时处理及病情监测的要求。利用本研究提出的基于紧密度的Grey-sigmoid核函数方法,在满足分类精度的同时,可有效减少分类时间,提高基于高光谱遥感图像的小麦全蚀病实时监测能力(表2)。 表2 2种Sigmoid核函数的支持向量机分类的对比Table 2 The comparative results for different SVM methods based on Sigmoid kernel 注:这里的精确度、Kappa值和处理时间均为实验均值。 Note: The accuracy, Kappa value and processing time are the mean. 由于目标地物的特征差异,高光谱图像的形成受到红移和噪声的影响,不可避免的具有模糊、不均等特点[12]。本研究在图像分块的基础上,将小麦乳熟期原始光谱图像分割成6个子块进行并行处理,采用基于紧密度的Grey-Sigmoid核函数方法进行实验时,同时采用传统Sigmoid核函数进行分类对比试验(图3),各种方法的平均精确度、平均Kappa值和处理时间见表2。 图3 利用图像分块进行分类的并行处理结果Fig.3 Parallel processing results using image block classification 从表2可以看出,采用Grey-Sigmoid核函数的支持向量机在全蚀病程度的分类上精确度和置信度(Kappa值)均与传统的Sigmoid核函数持平且略有提升,而处理时间则有比较明显的减少。根据图3显示的分类结果,相对于传统的Sigmoid核函数,基于Grey-Sigmoid核函数的支持向量机并行处理算法对于分类背景中的野值和噪声有更好的过滤性能,且对于小麦的边缘分类状况有更好的识别度(例如子块5和子块6中产生的较为明显的分类误差)。 针对传统Sigmoid核函数的支持向量机方法中存在的对野值和边缘分类的敏感问题,本文研究了一种基于紧密度的Grey-Sigmoid核函数,不仅考虑了样本与所在类中心之间的距离,也考虑了样本间的聚类信息。在特征空间中,可以用一个紧凑的球或超球将样本集包围起来,此时,样本间的紧密度可以通过包围样本的最小球的半径来度量。对分布在半径内、外的样本,分别计算其灰度。由于考虑样本的灰度,该方法更有效的将野值噪声和样本中的有效样本进行区分,从而更好地反应样本在支持向量机的目标函数的作用。 为了更好地评价基于紧密度的Grey-Sigmoid核函数的分类性能和抗噪能力,分别使用UCI测试数据和田间试验获取的小麦全蚀病光谱图像进行对比实验。结果表明,本文提出的基于紧密度的Grey-Sigmoid核函数支持向量机具有更好的抗噪性及分类能力,结合图像分块的并行处理方法,可以有效地提高支持向量机的运算速率。 [1] DATCU M,SEIDEL K,PELIZARRI A,et.al. Image information mining and remote sensing data interpretation[C]//IEEE Geoscience and Remote Sensing Symposium, 2000. Proceedings. IGARSS 2000. IEEE 2000 International. IEEE, 2000(7):3057-3059. [2] 周成虎,骆剑承,杨晓梅. 遥感影像地学理解与分析[M].北京:科学出版社,1999. [3] SHAH C A, WATANACHATURAPORN P, VARSHNEY P K, et al. Some recent resuIts on hyperspectral image classification[C]//IEEE Workshop on Advances in Techniques for Analysis of Remotely Sensed Data, 2003 IEEE Workshop on. IEEE, 2004:346-353. [4] NEMMOUR H, CHIBANI Y. Multiple support vector machines for land cover change detection: An application for mapping urban extensions[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006,61(2): 125-133. [5] LINKER R, SEGINER I. Greenhouse temperature modeling: a comparison between sigmoid neural networks and hybrid models[J]. Mathematics and computers in simulation, 2004,65: 19-29. [6] CAMPS-VALLS G, MARTN-GUERRERO J D, ROJO-LVAREZ J L, et al. Fuzzy sigmoid kernel for support vector classifiers[J]. Neurocomputing, 2004, 62: 501-506. [7] CHERKASSKY V, MA Y. Practical selection of SVM parameters and noise estimation for SVM regression[J]. Neural Networks, 2004,17(1): 113-126. [8] 刘涵,刘丁. 基于模糊sigmoid核的支持向量机回归建模[J]. 控制理论与应用, 2006,23(2): 204-208. [9] 张翔,肖小玲,徐光祐. 基于样本之间紧密度的模糊支持向量机方法[J]. 软件学报, 2006, 17(5): 951-958. [10] 郭三党,王玲玲,刘思峰,等. 基于最大灰色关联度的聚类方法分析[J]. 数学的实践与认识, 2013, 43(6): 195-201. [11] 黄卫春,刘建林,熊季艳. 基于样本—特征加权的模糊核聚类算法研究及应用[J].计算机工程与科学, 2014. 36(1):169-174. [12] ZHAO J W, CHEN Q, HUANG X, et al. Qualitative identification of tea categories by near infrared spectroscopy and support vector machine[J]. Journal of Pharmaceutical and Biomedical Analysis, 2006,41(4): 1198-1204. (责任编辑:马红春) Studyonhyperspectralremotesensingimageclassificationmethodbasedonthegrey-sigmoidkernelfunctionsupportvectormachine WANG Haolin1, GUO Wei2, SHI Yue2, QIAO Hongbo2 (1.Senior High School of Zhengzhou Foreign Language New Fengyang School, Zhengzhou 450001, China; 2.College of Information and Management Science, Henan Agricultural University, Zhengzhou 450002, China) Since SVM is sensitive to the noises and outliers in the training set, a new SVM algorithm based on affinity Grey-Sigmoid kernel is proposed in the paper. The cluster membership is defined by the distance from the cluster center, but also defined by the affinity among samples. The remote sensing image classification experiments conducted in the field of wheat prove that, compared with the Grey-Sigmoid kernel function and Sigmoid kernel function of the traditional, it is faster in computational speed and there is no obvious loss in accuracy. hyperspectral remote sensing; support vector machine; image; classification TP205 :A 2016-05-06 国家自然科学基金项目(31301604);河南省科技攻关项目(122102110045) 王颢霖(1999-),男,河南郑州人,主要从事计算机应用研究。 乔红波(1978-),男,河南新野人,副教授,博士。 1000-2340(2017)03-0402-06
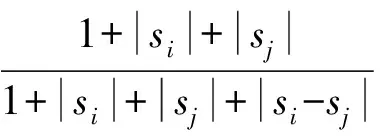
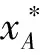


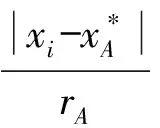
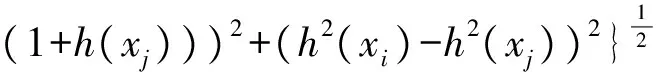
2 结果与分析



3 结论

