一种改进的归一化LMS算法

杨 坡，刘铸华

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225001)

一种改进的归一化LMS算法

杨 坡，刘铸华

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225001)

传统的归一化最小二乘(LMS)算法可以解决算法收敛速度和采样信号收敛误差之间的矛盾。通过对收敛步长的归一化处理，从而减小收敛过程的稳态误差。但是，这种算法却将收敛的步长变为固定，不利于算法的快速收敛。为此，提出一种改进的归一化LMS算法，将Sigmoid 函数变步长最小均方(SVSLMS)算法与归一化LMS算法结合，提高了归一化LMS算法的收敛速度。仿真结果表明，该算法性能较之归一化LMS算法、SVSLMS算法和普通LMS算法均更优异。

归一化最小二乘算法；Sigmoid 函数变步长最小均方算法；收敛速度

0 引 言

传统的最小二乘(LMS)算法因为良好的自适应性能而被广泛应用于雷达通信领域。然而，普通的LMS算法存在着收敛后稳态误差和收敛速度之间的矛盾[1]。当采用的算法收敛步长因子较大时，能加快收敛速度，但是稳态误差却也同时变大；反之，能带来较低的收敛速度和较小的稳态误差[2-3]。但是，系统应用往往需要较快的收敛速度的同时有着较小的稳态误差。归一化的LMS算法通过将收敛步长因子对信号功率归一化，从而解决了收敛速度和稳态误差这对矛盾。但是此时，归一化后的步长因子为固定的，不利于更好地对收敛进行加速。下面，将Sigmoid 函数变步长最小均方(SVSLMS)算法与归一化的LMS算法[4]进行结合，从而对归一化的LMS算法进行快速收敛优化。

1 改进的归一化LMS算法

将SVSLMS变步长算法和归一化的LMS算法进行结合，从而使结合后的算法同时具备变步长加快收敛速度和平衡收敛速度及稳态误差的双重效果。相对SVSLMS和归一化LMS算法，结合后的算法性能明显改善。

1.1 LMS算法

LMS算法通过对系统输出与期望响应之间的误差迭代收敛，从而使得系统输出最终稳定为期望响应。迭代过程中，误差逐步变小，当误差小于一定范围时，迭代结束。LMS算法一般应用于自适应滤波过程。每次迭代后的系统输出与期望响应之间的误差作为反馈值参与到下一轮的迭代过程中，通过系数不断调整，使得系统输出收敛于期望响应附近。

一般的LMS算法步骤如下：

(1) 采样信号系数起始设置：

W(0)=0

(1)

(2) 计算每次输入样本对应的输出值：

y(n)=WT(n)X(n)

(2)

(3) 与期望信号d(n)对比，每次产生样本信号对应的误差：

e(n)=d(n)-y(n)

(3)

(4) 对采样信号系数进行迭代更新：

W(n+1)=W(n)+2μX(n)e(n)

(4)

然后对系数迭代更新过程进行反复操作，其中要使得迭代结果收敛，则步长因子μ应该具备0<μ<1/λmax条件，λmax为采样信号自相关矩阵的最大特征值。通过选择不同的补偿因子，可以调整收敛的速度。但是，当为了提高收敛速度而加大μ时，其稳态误差会加大。因此，引入归一化的LMS算法。

1.2 归一化LMS算法

归一化的LMS算法通过改变步长因子来解决算法的收敛速度和稳态误差之间的矛盾。补偿因子需要用输入信号的功率值进行归一化处理，从而得到与输入信号功率有关的变步长因子μ，该因子随着输入功率改变而改变，从而实现较高收敛速度下较低的稳态误差[5]。对于归一化的过程可以归纳如下：

(1) 归一化步长因子计算：

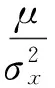
(5)

(6)

(2) 权系数更新过程：

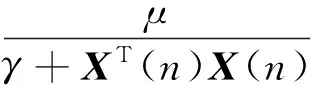
(7)

此时的步长因子随着输入功率的改变而改变，从而使得归一化LMS算法同时具备收敛速度及稳态误差双重保证。这里的γ是为了避免假分数出现而设定的微小量。归一化后的LMS算法虽然解决了收敛速度与稳态误差之间的矛盾，但是步长因子仅由输入功率唯一决定，一旦输入信号确定，步长因子在整个迭代过程中固定，这样不利于收敛算法的加速。为此，接下来介绍一种加速收敛过程的变步长SVSLMS算法。

1.3 SVSLMS算法

为最快取得收敛值，陈景繁等学者提出了SVSLMS算法，其步长μ(n)有如下的形式：

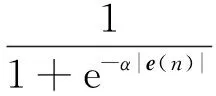
(8)

随着误差减小，步长因子逐步跟着变小。当收敛开始时，误差较大，迭代步长因子也较大，可以使得样本快速收敛。当逐渐进入算法收敛后，误差的减小使得步长因子变小，从而实现稳态误差的减小。β为步长因子取值范围决定项，α则会影响收敛算法的最终稳态误差。通过步长因子在迭代过程中随误差改变而改变的过程，从而实现算法收敛的加速进行。但是，收敛速度的快慢仅随着误差的改变而改变，并不能充分考虑到样本量的权重。

在此，可以发现归一化的LMS算法虽然可以通过用输入功率进行步长因子的归一化，从而实现收敛速度与收敛稳态误差的平衡，但却把步长因子固定为仅由输入功率唯一决定的固定量。而SVSLMS算法虽然可以加快算法的收敛过程，但是收敛过程只随着误差改变而改变，并不能得到较好的收敛速度与稳态误差平衡。这里，将这2种算法进行结合，以使得算法同时具备2种算法的优点。

1.4 改进的归一化LMS算法

对归一化的LMS算法引入SVSLMS算法的思想，从而实现2种算法的结合。此时，提出一种改进的归一化LMS算法，其步长因子的表达形式如下：

(9)

权系数迭代过程如下：

W(n+1)=W(n)+2μ(n)X(n)e(n)

(10)

2 仿真与分析

通过分析归一化LMS算法、SVSLMS算法及改进算法在信号自适应处理中的应用，可以了解改进算法的性能。仿真中取信号为余弦信号，幅度为1，噪声为20 dB高斯白噪声，分别采用归一化LMS算法、SVSLMS算法及改进算法对信号进行滤波，期望信号为未加噪声的余弦信号，幅度为4。其中SVSLMS算法及改进算法中采用的β=2，α=20。归一化LMS算法中采用的μ=0.1。通过对3种算法的收敛速度、稳态误差对比来了解改进算法的性能改善。

分别对比图1和图2，图4和图5，可以发现归一化LMS算法虽然较之SVSLMS算法有稳态误差小的特点，但是，归一化LMS算法明显比SVSLMS算法的收敛速度慢。由图1、图2、图3对比可见，归一化LMS算法的误差大致在40次迭代处稳定下来，SVSLMS算法在15次左右稳定下来，而改进算法在10次左右稳定下来。可见改进算法吸取了SVSLMS算法快速收敛的特点。而对比图4、图5、图6可见，归一化LMS算法和改进算法较之SVSLMS算法的稳态误差要小，可见改进算法吸取了归一化LMS算法的稳态误差小的特点。

3 结束语

分析比较了归一化LMS算法、SVSLMS算法和改进算法的收敛速度和稳态误差性能，改进算法分别吸取了归一化LMS算法稳态误差小的特点和SVSLMS算法的快速收敛特点，通过算法的结合取双方优点来弥补相互的缺点，从而实现算法性能的提升。改进算法在收敛速度和稳态误差性能上均有较大提升。

[1] 成磊,葛临东.变步长 LMS 算法性能比较与仿真[J].信息工程大学学报,2004,4(4):70-73.

[2] 李杨,韩鹏,檀虎.几种变步长 LMS 算法的性能分析与比较[J].国外电子测量技术,2013(3):28-30.

[3] 吕春英,敖伟,张洪顺.一种新的变步长 LMS 算法[J].通信技术,2011,44(3):11-14.

[4] 张银行,杨辉媛,宋志国.基于归一化 LMS 算法的自适应滤波器设计[J].吉首大学学报,2012,33(2)：54-56.

[5] 曾召华,刘贵忠,赵建平.LMS 和归一化 LMS 算法收敛门限与步长的确定[J].电子与信息学报,2004,25(11):1469-1474.

AnImprovedNormalizedLMSAlgorithm

YANG Po,LIU Zhu-hua

(The 723 Institute of CSIC,Yangzhou 225001,China)

The traditional normalized least mean square (LMS) algorithm can solve the contradiction between convergence speed of the algorithm and convergence error of the sampled signals.By normalizing the convergence step-size,the steady-state error of convergence process is reduced.But this algorithm turns the convergence step-size into fixed value,which is unfavorable to fast convergence of the algorithm.Thus this paper proposes an improved normalized LMS algorithm,which combines the Sigmoid variable step-size least mean square (SVSLMS) algorithm with the normalized LMS algorithm,improves the convergence speed of normalized LMS algorithm.Simulation results show that the performance of the proposed algorithm is better than that of normalized LMS algorithm,SVSLMS algorithm and ordinary LMS algorithm.

normalized least mean square algorithm;Sigmoid variable step-size least mean square algorithm;convergence speed

TN911.7

：A

：CN32-1413(2017)04-0059-03

10.16426/j.cnki.jcdzdk.2017.04.015

2017-05-17