运用双向LSTM拟合RNA二级结构打分函数

王 帅 蔡磊鑫 顾 倜 吕 强,2

1(苏州大学计算机科学与技术学院 江苏 苏州 215006)2(苏州大学江苏省计算机信息处理技术重点实验室 江苏 苏州 215006)

运用双向LSTM拟合RNA二级结构打分函数

王 帅1蔡磊鑫1顾 倜1吕 强1,2

1(苏州大学计算机科学与技术学院 江苏 苏州 215006)2(苏州大学江苏省计算机信息处理技术重点实验室 江苏 苏州 215006)

RNA二级结构的打分函数在RNA二级结构预测中扮演着越来越重要的角色。目前对RNA二级结构的打分函数并没有很好地抓住RNA的折叠机制。我们认为递归神经网络层与层之间的信息传递方式和RNA 的折叠方式有相似之处。提出使用双向LSTM(Long Short term Memory)神经网络对RNA二级结构进行打分。在数据集ASE(长度小于500)，以及CRW(大部分长度大于1 000)上，进行了三项实验。通过拟合SEN(Sensitivity)与PPV(Specificity)打分函数确定了在目标函数为mean_squared_error时拟合效果最好；进而对比较复杂的打分函数MCC(Matthews correlation coefficient)进行拟合；最后实验得出双层双向LSTM模型的结果优于单层双向LSTM模型的结果。通过实验，得到的打分函数包含了碱基序列的全局属性。实验结果表明LSTM深度神经网络模型可以很好地拟合RNA二级结构的打分函数。

RNA 打分函数 二级结构 双向LSTM

0 引 言

众所周知，四种核糖核苷酸以氢键联接碱基(A对U;G对C)形成RNA的二级结构。RNA作为生物遗传信息传递和复制的重要组成部分，其结构非常复杂。RNA分子式在生物体内参与各种如细胞分化、代谢、记忆存储等重要生命活动的一类大分子，其常见种类有rRNA、mRNA、tRNA。 其中除tRNA分子量较小外，其余RNA分子都具有非常大的分子量且结构复杂。传统的物理、化学结构预测方法只适用于测量分子量较小的RNA。 而针对大分子量的RNA二级结构预测，使用计算机技术预测是一条行之有效的方法。预测RNA 二级结构[1]一般采用最小自由能模型。该模型假定真实的RNA 会折叠成一个具有最小自由能[3]的二级结构。而二级结构中的每段模体[6]都有相应的自由能计算方法。一般茎区[6-7]的自由能为负值，环区自由能为正值，茎区越长其自由能越小，因此可以近似的认为，配对的碱基[4]使自由能降低，没有形成配对的碱基使自由能升高。

常用的数据拟合方法有线性拟合、曲线拟合、二次函数拟合、数据的n次多项式拟合等，但这些方法不能拟合出比较好的RNA二级结构打分函数。基于序列的机器学习方法有神经网络、支持向量机和隐马尔可夫模型等，尤其是递归神经网络，在基于序列的机器学习方法中取得了比较好的成果。例如：Oriol Vinyals等[24]使用递归神经网络在人工智能连接计算机视觉和自然语言处理方面做出了卓越贡献，在Pascal数据集上BLEU分数由25提高到59；Ilya Sutskever等[25]使用递归神经网络在机器翻译领域作出了重大贡献，在WMT-14数据集中英文翻译中文的BLEU分数从33.3提高到36.5。因为本文的生物信息特征都是基于序列提取的，所以使用双向LSTM[2,8]来对每个RNA序列的整条链信息进行建模，为了避免机器学习过程中出现过拟合现象，本文在模型训练过程中加入了处理过拟合的Dropout技术。实验结果表明，基于双向LSTM[2,8]的深度神经网络明显提高了RNA二级结构打分函数的准确率，另外，Dropout对防止过拟合也起了重要作用。

1 拟合打分函数的数据准备及模型方法

1.1 数据集和评估方法

本文使用ASE以及CRW数据集作为实验的研究对象，在ASE数据集中，总共有450条RNA，RNA序列的长度在200到500之间，每条RNA都有6 000种结构，也就是有2 700 000条序列作为实验对象，在CRW数据集中总共有上千条RNA，本文取其中的100条作为实验对象，序列的长度在1 000以上，每条RNA都有5 000种结构，有500 000条序列作为实验对象。在机器学习和模式识别领域中：训练集是用来估计模型的；验证集是用来确定网络结构或者控制模型复杂程度的参数；测试集则是检验最终选择最优模型的性能。本文将训练集和验证集，以及测试集按照8∶1∶1的方式分配。

对于预测结果的评估，现阶段对RNA二级结构的打分函数绝大多数文献使用的是敏感性SEN(真实结构中所有的碱基对中被正确预测到的百分比)跟特异性PPV(在所有预测到的碱基对中正确预测的百分比)进行测量。一般的预测方法很难两者兼顾，总是偏向于一边，因此通常用马休兹相互作用系数MCC折中衡量。另一种打分函数叫作MEA(MaxExpect Accuracy)，MEA的预测包括了最优结构(拥有最高的碱基配对的准确性期望)和次优结构两种研究对象。

但是MEA作为对RNA二级结构的打分函数并不准确，因为对于同一RNA结构，在其他标准打分函数(MCC、SEN、PPV)高的同时，MEA并不一定同样高，所以能够得到一种比较精确的打分函数是目前亟待解决的问题。本文中对于此模型主要的评估指标有MCC、SEN以及PPV。

1.2 特征提取以及计算目标变量

本文对每条RNA的几千种结构都进行了特征提取，以及对目标变量的计算。

对特征的提取使用的是四种碱基类型A(腺嘌呤核糖核苷酸)、T(胸腺嘧啶核糖核苷酸)、U(尿嘧啶核糖核苷酸)、G(鸟嘌呤核糖核苷酸)作为对RNA二级结构打分的第一个特征属性，输入时使用四种数字分别表示这四类碱基；另一个特征属性为RNA序列的配对情况，哪两个碱基互相配对，特征表示为与此碱基配对碱基的序号，没有形成配对的碱基用零来表示。

目标变量主要包括SEN、PPV和MCC，其计算公式如下：

式中，TP表示正确预测碱基对的个数；FN表示真实结构中存在但没有被正确预测出的碱基对个数；FP表示真实结构中不存在却被错误预测的碱基对个数；TN表示正确预测的不配对的碱基的个数。

1.3 模型及训练

LSTM是对传统递归神经网络的改进，它用记忆单元替换了传统递归神经网络的隐函数。这样的改进使LSTM可以记忆比传统递归神经网络更长范围的上下文。本文使用的LSTM模型表述如下：

it=σ(Wxixt+Whiht-1+bi)

(1)

ft=σ(Wxfxt+Whfht-1+bf)

(2)

ct=ftct-1+ittanh(Wxcxt+Whcht-1+bc)

(3)

ot=σ(Wxoxt+Whoht-1+bo)

(4)

ht=ottanh(ct)

(5)

(6)

式中，σ表示sigmoid激活函数，it、ft、ot分别代表输入门、遗忘门、输出门。ct代表记忆细胞，ht代表隐层输出。记忆细胞存储了序列的过去信息，输入门控制信息的输入，也就是控制当前输入的信息是如何影响记忆细胞的。

众所周知，单向的递归神经网络[10]只是从序列的一端向另一端逐个读取输入数据，所以在任意的时刻，递归神经网络里存储的数据只有当前和过去的信息。然而向RNA序列上的一个碱基，它既与它前面的碱基相关，也会与它后面的碱基相关。对于这样的问题递归神经网络的每个时间点的输出应该包含两个方向的信息，所以单向的递归神经网络是不适合对RNA序列进行建模的。

图1 展开的双向LSTM图

本文使用的模型是基于Theano[5]和Keras(http://keras.io/)编写的。图2为模型整体架构图：模型中包含了两层双向LSTM，第一层的隐节点数为40，第二层的隐节点数为20。第二层双向LSTM的输出再输入给Dense全连接层，Dense层的输出为拟合后的打分值。为了避免过拟合现象，全连接层的后面加入了Dropout层[11]，Dropout的比率为0.5，最后还有一个Logistic层[12]用于分类。对迭代次数的设置为：外层设为20，内层设为动态迭代次数，当训练集的损失函数与验证集的损失函数相差小于0.5%时内层迭代停止。

图2 模型架构图

常规模型一般应用于等长序列的训练，并且均为单层模型，对激活函数也并未做出适当调整，极易出现过拟合现象。所以本文设计的模型架构不同于一般模型，训练过程也和一般模型的训练过程有所不同。另外由于每次训练的序列长度不等，所以运用了随机逐条的方法进行训练，每条序列有几千种结构。优化算法使用Keras实现的Adam[13]，Adam的学习速率设为0.005，目标函数设为mean_squared_error(均方误差公式)、mean_squared_logarithmic_error(均方对数误差公式)，其他参数保持默认值。

按照此模型在本地机器上(CPU：Intel(R) Xeon(R) E5-2620 v2 @ 2.10 GHz 内存：64 GB)训练一个batch数据平均需要1～3分钟。

2 结果与分析

2.1 在ASE数据集上对回归目标变量为SEN与PPV的结果分析

因为CRW数据集上的RNA序列长度都大于1 000，有的序列长度甚至达到了3 000，所以双向LSTM模型对CRW数据集上的拟合需要对模型节点数进行增加，对迭代次数也要进行相应的提高，总体效果与ASE数据集相差不大。所以下面本文着重对ASE数据集进行结果分析。

本文根据皮尔森相关系数PCC[20](Pearson correlation coefficient)，以及标准差SD(Standard Deviation)作为对拟合打分函数前后的评价标准来评价模型对目标变量拟合的好坏。

在目标函数为mean_squared_error下，拟合SEN后的分数与SEN的PCC在[0.2，0.5]之间，SD由SEN的0.02左右降为拟合SEN目标变量的0.005左右。在目标函数为mean_squared_logarithmic_error下，拟合后SEN的分数与SEN的PCC在[0.1，0.3]之间，SD由SEN的0.02左右降为拟合数据的0.005左右。

在目标函数为mean_squared_error下，拟合PPV后的分数与PPV的PCC在[0.05，0.2]之间，SD由PPV的0.02左右降为拟合PPV目标变量的0.01左右。在目标函数为mean_squared_logarithmic_error下，拟合后PPV的分数与PPV的PCC在[0.05，0.2]之间，SD由PPV的0.02左右降为拟合数据的0.005左右。

为了进一步观察两个目标函数的优劣性，本文比较了两者在训练集、验证集，以及测试集上的loss值。图3描述了在目标函数为mean_squared_error下拟合SEN的测试集与验证集的loss变化，训练集与验证集的loss值最终趋于相同，同时测试集的Test score为0.023 945 9，比训练集与验证集的loss值低了一些；图4描述了在目标函数为mean_squared_error下拟合PPV的测试集与验证集的loss变化，训练集与验证集的loss值最终趋于相同，同时测试集的Test score为0.001 214 16，比训练集与验证集的loss值低很多，起到了明显的拟合效果。

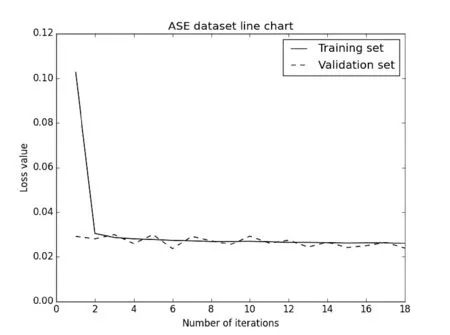
图3 在mean_squared_error下SEN测试集与验证集的loss变化

图4 在mean_squared_error下PPV测试集与验证集的loss变化

2.2 在ASE数据集上对目标变量为MCC的结果分析

本文在与SEN跟PPV相同的数据集上拟合MCC目标变量，因为MCC的计算公式囊括了SEN与PPV的内容，并复杂于上述两种打分函数，所以在同一模型的情况下拟合MCC的打分函数并不是很理想。因此将模型的外层迭代次数增加到40，结果有了一些提升，最终与其他两种打分函数的拟合情况相差并不是很大。

在目标函数为mean_squared_error下，拟合MCC后的分数与MCC的PCC在[0.05，0.35]之间，相关性没有SEN的相关性好，但是高于PPV的相关性。SD由MCC的0.02左右降为拟合数据后的0.005左右。表1代表了两层双向LSTM对MCC打分函数的拟合情况。

表1 在分数为MCC下的双层双向LSTM的拟合情况

为了进一步观察拟合MCC打分函数的情况，本文对其训练集，以及验证集的loss进行分析。图5描述了在目标函数为mean_squared_error下拟合MCC的训练集与验证集的loss变化，同时测试集的Test score为0.001 435 58，比训练集与验证集的loss值低，起到了明显的拟合效果。

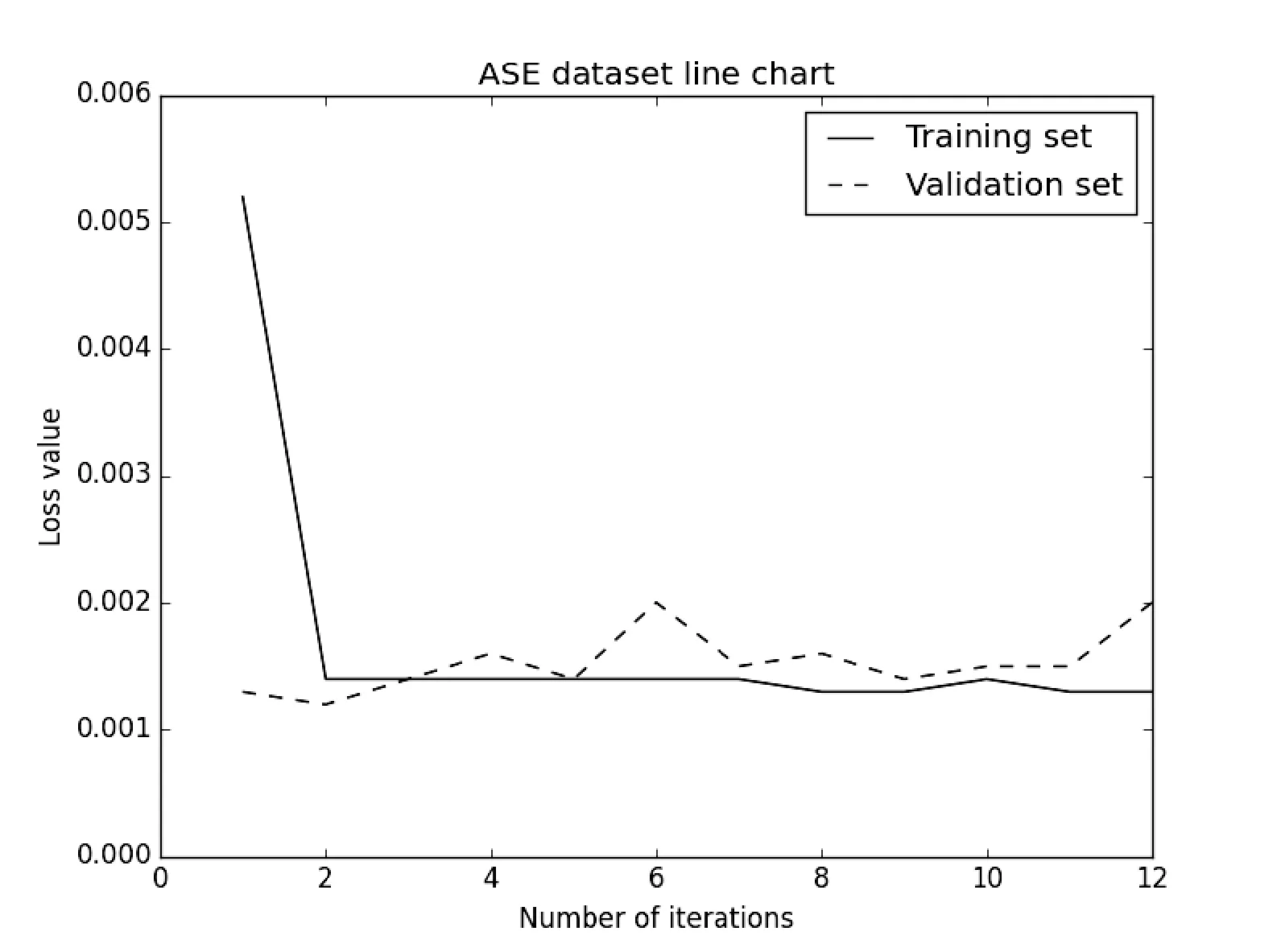
图5 在mean_squared_error下MCC测试集与验证集的loss变化

2.3 在ASE数据集上对两层双向LSTM与单层双向LSTM模型的结果比较

一般情况下，对拟合行为应用双向LSTM只需要单层的双向LSTM即可，但为了能够得到更好的拟合效果，并对两层的双向LSTM与单层的双向LSTM进行性能的比较，本文对同样的数据集也进行了单层的双向LSTM实验。由于数据集比较大，每条RNA的测试集的目标变量个数已经达到600，所以在做表时提取了测试集的六十分之一作为代表。表2给出了两层双向LSTM与单层双向LSTM对打分函数为SEN的拟合情况；表3给出了两层双向LSTM与单层双向LSTM对打分函数为PPV的拟合情况，本文提取出数据集中的同一条RNA序列，并且在两个模型的其他条件均相同的情况下，可以明确地看出两层的双向LSTM的拟合效果优于单层的双向LSTM拟合效果。

表2 在分数为SEN下的双层双向LSTM与单层双向LSTM模型的比较

表3 在分数为PPV下的双层双向LSTM与单层双向LSTM模型的比较

同时，本文对两个模型进行了皮尔森相关系数以及标准差的分析，在相同条件的情况下，拟合SEN后的分数与SEN的PCC由双层双向LSTM的区间[0.2，0.5]降为单层双向LSTM的区间[0.1，0.35]，相关性下降；拟合PPV后的分数与PPV的PCC由双层双向LSTM的区间[0.05，0.2]降为单层双向LSTM的区间[0.05，0.15]，相关性下降。SD由拟合SEN的双层双向LSTM的0.005左右增长为单层双向LSTM的0.01左右；拟合SEN的双层双向LSTM的0.005左右增长为单层双向LSTM的0.008左右，稳定性增强。

双层双向LSTM优于单层双向LSTM的主要原因在于数据集的第一维为300左右，第二维为2，若是只有一层双向LSTM的模型，则维度直接降为10×10，维度变化太过陡峭；若是有两层双向LSTM模型的话，在第一层双向LSTM维度可以减为20×20，继而再进入第二层双向LSTM时维度变为10×10，这样可以令维度变化比较舒缓，可以更好地训练数据集，进而对结果能够得到更大的优化。

2.4 在ASE数据集上Linear regression、双向GRU(Gated Recurrent Unit)、双向LSTM与改进的双向LSTM四种算法的结果比较

本文提到了对RNA二级结构的打分函数有MEA(MaxExpect Accuracy)，此打分函数拥有最高碱基配对的准确性期望。MEA[16]计算公式如下：

(7)

Pbp(i,j)为形成配对碱基i与j的概率，Pss(k)为未形成配对的碱基k的概率。

由于MEA对RNA二级结构的打分并不是很准确，所以本文将配对碱基概率与单链碱基概率按照碱基类型分别在A、G、C、U这四类碱基上分别加上参数，总共是八个参数，利用批量梯度下降算法[17]训练上述参数,进而对打分函数进行拟合。

另一种为双向GRU[19](Gated Recurrent Unit)模型，它比LSTM模型简单易于实现，两者在不同问题上各有优势，两个模型主要区别在于记忆单元内部的构造不同。实现公式如下：

rt=σ(Wxrxt+Whrht-1+br)

(8)

zt=σ(Wxzxt+Whzht-1+bz)

(9)

(10)

(11)

式中，rt和zt分别代表重置门和更新门，ht类似于LSTM的记忆细胞ct。此模型允许丢弃与未来不想关的信息，从而产生更加简洁的输入信息。此模型与双向LSTM相比其他参数不变。

本文还将双向LSTM算法进行了改进，传统的双向LSTM是将前馈神经网络(forward)与后馈神经网络(backward)的输出进行了简单的加和，本文将其运算转换为加和的sigmoid函数，具体公式如下：

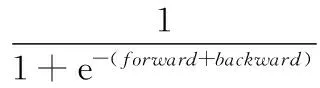
(12)

同时对模型节点数进行了适当的增加，迭代次数也增加到60。表4给出了四种算法的结果比较，可以明确地看出改进后的双向LSTM算法比另外三种算法效果要好5%左右。

表4 Linear regression、双向GRU、双向LSTM与改进的双向LSTM四种算法在目标变量为MCC上的结果比较

皮尔森相关系数值越大，其与原分数的相关性越强，标准差越小说明分数摆动幅度越小，越稳定。从表4可以看出，改进后的双向LSTM的相关性是这四种算法中最好的，稳定性也是最好的，并且这四种算法的相关性与稳定性在原分数的基础上都有所增强。

3 拟合打分函数的结果验证

3.1 对于含假结的RNA的实验验证以及适用程度

在数据集为RNASTRAND中，含有特殊结构(假结[18]Pseudoknots)的RNA有ASE_00001-ASE_00009以及ASE_00011，本文围绕含有假结的RNA进行了实验结果比对，假结结构如图6所示。

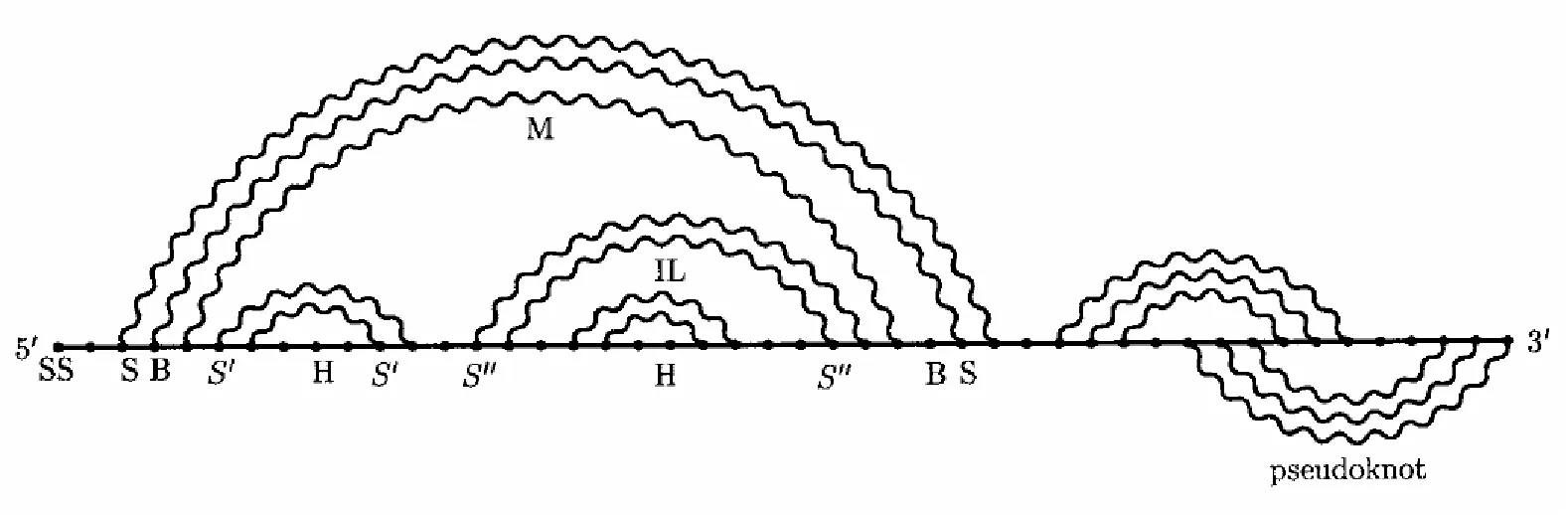
图6 含有假结的RNA序列

本文应用违反率VR(Violation rate)来对经过改进后的双向LSTM模型得出的打分函数与SEN、PPV和MCC三种标准打分函数进行比较。违反率是在标准打分函数排序的情况下所对应模型输出结果排序的违反情况。表5给出了三条含假结的RNA在四种算法上的违反率，可以看出LR算法表现比较差，经过改进后的双向LSTM效果最好。

表5 含假结的RNA在四种算法上MCC违反率的情况

如表5所示，模型越复杂、模型节点数越多、对特征信息记忆得越好其违反率就会越低。ASE_00004与ASE_00006经过改进后的双向LSTM效果变好了一些，但是在ASE_00005上效果会反弹，造成这种现象的原因有两点：第一点ASE_00005此序列的天然结构中含有两个假结结构，在模型训练时，训练集中并不是所有的结构都会含有两个假结，所以模型在训练时会因假结结构造成困扰，以至于经测试集得出的打分函数会出现反弹的现象；第二点在训练模型时，所用的数据集是经过遗传算法[21]以及随机拆取RNA序列的配对情况得出的，而遗传算法有随机性，所以得到的结构也具有随机性。因此结果会出现反弹的情况。

表6给出了三条含假结的RNA在改进的双向LSTM模型上对三种标准打分函数的优劣情况，可以看出改进后的双向LSTM对SEN打分函数的拟合效果比较好一些，对PPV的拟合效果比较差一些。造成此类效果的原因是：在医学上，高敏感性与高特异性不可兼得，高敏感性则低特异性，高特异性则低敏感性。在本文所使用的训练集中大部分的SEN值是比较高的，所以出现了拟合打分函数高敏感性低特异性的现象，然而马修兹相互作用系数MCC是两者的折中衡量，在经过2.2节中迭代次数的增加得出了介于两者之间的结果。

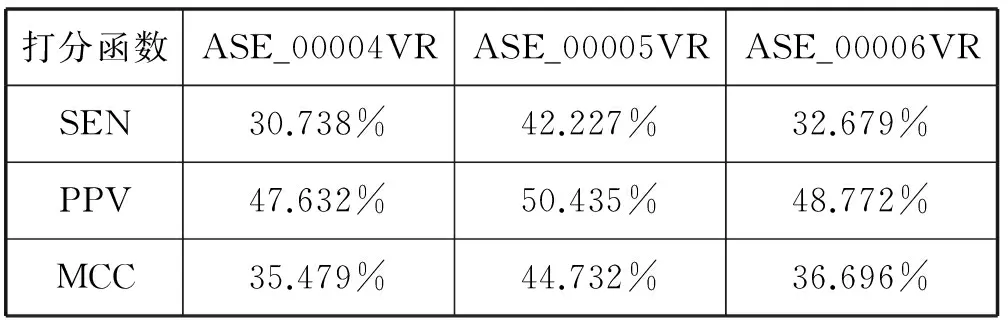
表6 含假结的RNA在改进后的双向LSTM模型上三种打分函数的违反率情况

3.2 对RNA STRAND中最常见的RNA类型的实验验证以及适用程度

在数据集为RNASTRAND中，含有原核生物的三种核糖体RNA[22]，分别为：CRW_00020-CRW_00029十条RNA序列的16S Ribosomal RNA；CRW_00467-CRW_00476十条RNA序列的23S Ribosomal RNA；CRW_00548-CRW_00557十条RNA序列的5S Ribosomal RNA。其中S为沉降系数[23]，本文训练的数据集包括了这三种比较常见的核糖体RNA。表7代表了在三种核糖体RNA中，改进后的双向LSTM对三种打分函数的拟合情况。

表7 在三种核糖体RNA中，改进后的双向LSTM对三种打分函数的拟合情况

如表7所示，在5S Ribosomal RNA上拟合效果最好，在23S Ribosomal RNA上拟合效果最差，造成这样的原因主要两点：其一，序列长度越短，其拟合情况越好；序列长度越长，拟合效果就越差，5S的序列长度一般在120左右，而23S的序列长度达到了2 900以上。其二，在RNA的二级结构中，序列比较长的RNA会出现各种环以及假结的概率很大，对模型的训练造成了一定的困难；而序列比较短的RNA出现假结的概率比较低，模型的训练就会比较顺利，进而拟合出的打分函数也相对比较准确。

4 结 语

本文基于双层双向LSTM的深度神经网络对RNA的二级结构进行打分，在ASE以及CRW数据集上分别对SEN、PPV和MCC三种打分函数进行了拟合。本文提出的模型很大的一个特点是它可以接受不同长度的RNA序列作为输入，这样模型就能够抓住每个碱基的全局信息,并且此模型同样适用于带假结的RNA二级结构预测。实验中通过在模型的全链接层后面添加Dropout层来减轻过拟合现象。由于本文的数据集是由序列长度小于500以及大于1 000的RNA序列组成。由于长序列在模型训练时对碱基的特征信息的叠加比较繁杂，所以在预测长度超过1 000的RNA序列时，预测结果往往没有预测长度小于500的RNA序列准确率高。所以，下一步我们通过增加数据集里的RNA数量。以及对模型的进一步改进来提升模型的精度。

[1] Mathews D H,Sabina J,Zuker M,et al.Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure[J].Journal of Molecular Biology,1999,288(5):911-940.

[2] Informatik F F,Schmidhuber J.LSTM Can Solve Hard Long Time Lag Problems[C]//Advances in Neural Information Processing Systems,1999:473-479.

[3] Heffernan R,Paliwal K,Lyons J,et al.Improving prediction of secondary structure,local backbone angles,and solvent accessible surface area of proteins by iterative deep learning[R].Scientific Reports,2015,5:11476.

[4] Cheng J,Randall A Z,Sweredoski M J,et al.SCRATCH:a protein structure and structural feature prediction server[J].Nucleic acids research,2005,33(S2):W72-W76.

[5] Bastien F,Lamblin P,Pascanu R,et al.Theano:new features and speed improvements[J].arXiv preprint arXiv:1211.5590,2012.

[6] Batey R T,Rambo R P,Doudna J A.Tertiary Motifs in RNA Structure and Folding[J].Angewandte Chemie,1999,38(16):2326.

[7] Gorodkin J,Stricklin S L,Stormo G D.Discovering common stem-loop motifs in unaligned RNA sequences[J].Nucleic Acids Research,2001,29(10):2135-2144.

[9] Björkholm P,Daniluk P,Kryshtafovych A,et al.Using multi-data hidden Markov models trained on local neighborhoods of protein structure to predict residue-residue contacts[J].Bioinformatics,2009,25(10):1264-1270.

[10] Tieleman T,Hinton G.Lecture 6.5-rmsprop:Divide the gradient by a running average of its recent magnitude[J].COURSERA:Neural Networks for Machine Learning,2012,2.

[11] Schmidhuber J,rgen.Learning unambiguous reduced sequence descriptions[C]//International Conference on Neural Information Processing Systems.Morgan Kaufmann Publishers Inc,1991:291-298.

[12] Cutlip D E,Windecker S,Mehran R,et al.Clinical end points in coronary stent trials:a case for standardized definitions[J].Circulation,2007,115(17):2344-2351.

[13] Moody J,Hanson S,Krogh A,et al.A simple weight decay can improve generalization[J].Advances in neural information processing systems,1995,4:950-957.

[14] Srivastava N,Hinton G,Krizhevsky A,et al.Dropout:A simple way to prevent neural networks from overfitting[J].The Journal of Machine Learning Research,2014,15(1):1929-1958.

[15] Schuster M,Paliwal K K.Bidirectional recurrent neural networks[J].Signal Processing,IEEE Transactions on,1997,45(11):2673-2681.

[16] David H Mathews.Using an rna secondary structure partition function to determine confidence in base pairs predicted by free energy minimization[J].Rna,2004,10(8):1178-1190.

[17] Nicolaos B Karayiannis.Reformulated radial basis neural networks trained by gradient descent[J].Neural Networks,IEEE Transactions on,1999,10(3):657-671.

[18] Cao S,Chen S J.Predicting RNA pseudoknot folding thermodynamics[J].Nucleic Acids Research,2006,34(9):2634-2652.

[19] Chung J,Gulcehre C,Cho K H,et al.Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling[J].Eprint Arxiv,2014.

[20] Arthur,Miranda,Neto.Pearson’s Correlation Coefficient:A More Realistic Threshold for Applications on Autonomous Robotics[J].Computer Technology and Application,2014(2):69-72.

[21] Deb K,Pratap A,Agarwal S,et al.A fast and elitist multiobjective genetic algorithm:NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.

[22] Schloss P D,Gevers D,Westcott S L.Reducing the Effects of PCR Amplification and Sequencing Artifacts on 16S rRNA-Based Studies[J].Plos One,2011,6(12):e27310.

[23] Schuck P,Rossmanith P.Determination of the sedimentation coefficient distribution by least-squares boundary modeling[J].Biopolymers,2000,54(5):328-341.

[24] Manning C D.Computational linguistics and deep learning[J].Computational Linguistics,2015,41(4):701-707.

[25] Dean J,Corrado G S,Monga R,et al.Large scale distributed deep networks[C]//International Conference on Neural Information Processing Systems.Curran Associates Inc,2012:1223-1231.

FITTINGTHERNASECONDARYSTRUCTUREOFSCORINGFUNCTIONWITHBIDIRECTIONALLSTM

Wang Shuai1Cai Leixin1Gu Ti1Lü Qiang1,21

(SchoolofComputerScienceandTechnology,SoochowUniversity,Suzhou215006,Jiangsu,China)2(ProvincialKeyLaboratoryforComputerInformationProcessingTechnology,SoochowUniversity,Suzhou215006,Jiangsu,China)

RNA Scoring Function plays a more and more important role in the RNA second structure prediction. At present, some scoring functions of RNA secondary structure do not have a good grasp of RNA folding mechanism. We believe that this mechanism and the way of information transmission between layers on recurrent neural network have similar aspects. Therefore, bidirectional Long Short Term Memory (LSTM) neural network was used to score the RNA secondary structure. We conducted three experiments based on the dataset ASE (length less than 1 000) and CRW (most of the length was greater than 1 000). By fitting the sensitivity (SEN) and specificity (PPV) scoring functions, it was determined that the fitting function was the best when the objective function is mean_squared_error. Then, we fitted the more complex scoring function Matthews Correlation Coefficient (MCC). Finally, the results of the two-layer bidirectional LSTM model were better than those of the single-layer bidirectional LSTM model. This article got the scoring function which contained global properties of the base sequence through experiments. Our approach shows that LSTM neural network model can fit the scoring function of RNA secondary structure well.

RNA Scoring function Secondary structure Bidirectional LSTM

TP391.4

A

10.3969/j.issn.1000-386x.2017.09.046

2016-11-27。国家自然科学基金项目(61170125)。王帅，硕士生，主研领域：生物信息计算。蔡磊鑫，硕士生。顾倜，硕士生。吕强，教授。