牛肉冻结过程中模拟及热值传递理论分析
唐 婉
王金锋1,2
李文俊1,2
谢 晶1,2
(1. 上海水产品加工及贮藏工程技术研究中心,上海 201306;2. 上海海洋大学食品学院,上海 201306)
牛肉冻结过程中模拟及热值传递理论分析
唐 婉1,2
王金锋1,2
李文俊1,2
谢 晶1,2
(1. 上海水产品加工及贮藏工程技术研究中心,上海 201306;2. 上海海洋大学食品学院,上海 201306)
以冰箱冻结牛肉为研究对象,考虑牛肉冻结过程中变物性特点,采用等效热容法处理相变潜热,再用计算流体力学(CFD)数值模拟技术对该冻结过程进行模拟,并建立描述三维食品冻结过程的微分方程,通过数值模拟得出冻结时间的模拟值,各测点(T1、T2、T3、T4、T5)模拟计算的冻结时间与试验冻结时间的误差分别为5.45%,3.90%,5.80%,4.24%,9.60%,各点实时温度的模拟平均误差是1.79 ℃。结果表明,数值模拟能较好地预测牛肉的冻结时间。
数值模拟;冻结时间;食品冻结;温度场
预测食品冻结时间,是对食品冻结过程研究的重要课题之一,冻结时间是衡量冻结设备优劣的重要标准,也是评价冻结食品品质的影响因素之一[1-2]。前人关于食品冻结时间的计算做了大量研究,周小清等[3]对比了现有的计算冻结时间的几种模型,研究发现对于液氮冻结圆柱状食品,国际制冷协会计算模型最为准确。Pham Q T 等[4]研究表明传统的计算食品冻结时间的经验公式在特定的环境下需要修正,才能保证计算的准确性。Becker B R 等[5]研究表明不同形状(无限大平板状、无限长圆柱状一级球形)的食品适用的计算食品冻结时间的模型不同。综上可知:传统的计算冻结时间的模型,具有局限性,而且只能获得热中心的冻结时间,随着计算条件的改变,计算公式需要修正,不具有普适性。CFD模拟技术被证明是计算食品冻结时间的有效方法之一[6-7],不仅可以计算食品的冻结时间,而且改变参数、计算条件等可以获取大量信息、数据,能直观地看到食品内部温度场分布,并实时监测提取食品内部任意一点的温度。
食品冻结是一个复杂的相变过程,其内部的相变发生在一定的温度区间,而非某一个温度值,因而潜热很难直接测量,所以前人在模拟食品冻结过程时,对物性的处理方法有大量的研究。屠建祥等[8]对比模拟了冻结过程中是否考虑物性变化对预测黄瓜冻结过程的影响,研究表明考虑物性变化的计算更符合实际。谢晶等[9]根据已有的食品物性经验公式,利用C语言编程计算,进而获得食品热物性随温度变化的多项式数学模型。Pham Q T等[10]对比分析了处理相变潜热的3种方法等效比热容法、焓法以及温度修正法,研究表明不同的相变处理方法影响了食品在模拟过程中计算的精度以及计算速度。李晓宇等[11]采用试验测量马铃薯的热物性参数,然后进行方程拟合。在以前的模拟研究中,也有假定冻结前后热物性参数为定值的[12]。殷刚[13]验证了利用等效比热容法处理相变潜热,用Basic语言编程对牛肉冻结时间进行数值计算,研究表明等效比热容法处理相变潜热对牛肉冻结时间不会产生影响,且比普朗克公式计算冻结时间精确,但是其存在不足之处,不能直观地看到牛肉内部温度分布情况,实时获得牛肉内部任意一点温度值。
鉴于以上研究,本试验利用Fluent 15.0模拟研究冰箱冻结牛肉内部温度场分布,调用文献[13~14]中利用等效热容处理相变潜热的方法(将食品的相变潜热换算到相变区间内的比容中),获得比热容和热导率的分段线性函数,引用到模拟环境,研究牛肉在冻结过程中内部温度的变化规律,实时监测牛肉内部各点温度,为更好地预测食品冻结时间以及优化、改进制冷设备做铺垫。
1 材料与方法
1.1 物理模型简化
如图1、2所示,本试验采用的是西门子冰箱,KK25F55TI型,牛肉置于冷冻室的中间层(尺寸400 mm×400 mm×130 mm),牛肉的尺寸100 mm×100 mm×70 mm的长方体。不考虑冷冻室内的管道设计对流场的影响。

图1 冰箱冷冻室以及食品摆放示意图
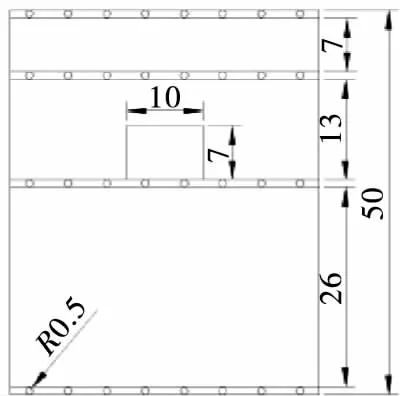
图2 食品摆放位置的主视图(cm)
1.2 控制方程及离散
本试验是研究牛肉在冰箱冷冻室蒸发盘管上的冻结过程,牛肉底部与蒸发盘管直接接触,牛肉上表面和侧面通过与空气自然对流传热,为简化模型作出以下假设:① 牛肉的初始温度均匀一致,且冻结环境温度一定;② 牛肉内部各向同性,相变温度一定;③ 牛肉的内部主要靠导热进行热传递,对流换热次之,且表面对流换热系数保持不变;④ 整个冻结过程,牛肉的密度保持不变(为1 050 kg/m3);⑤ 整个冻结过程中,边界条件保持不变;⑥ 牛肉内部非凝固区不考虑传质与流动。
基于上述假设,食品冷冻过程的导热微分方程为:
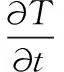
(1)
边界条件:
(1) 食品顶部和侧面第三类边界条件:
q=h(Tw-Tf),
(2)
式中:
Tw——牛肉表面的温度, K;
Tf——冰箱冷冻室内空气的温度(由试验测量获得),K。
表面对流换热系数按文献[15~16]方法赋值。
(2) 食品底面与蒸发盘管直接接触,近似认为牛肉下表面温度与蒸发盘管相同,由试验测量赋值,Tfood bottom(x,y,z)=Tban(x,y,z)=243 K。
(3) 在移动相界面上满足质量守恒和能量守恒:
Ts[S(t),t]=Tl[S(t),t]=Tp,
(3)
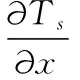
(4)
式中:
Ts——相界面上固相的温度,K;
Tl——相界面上液相的温度,K;
Tp——相界面上相变的温度,K;
λs——相界面上固相的导热率,W/(m·K);
λl——相界面上液相的导热率,W/(m·K);
h——比焓,kJ/kg;
ρ——密度,kg/m3。
初始条件:Tfood(x,y,z)=T0=278.15 K,食品温度按试验测量赋值。
1.3 牛肉冻结过程的数值模拟
本次模拟形状为长方体的牛肉:100 mm×100 mm×70 mm,而冰箱内冻结牛肉主要靠底部蒸发盘管的导热和表面的对流换热相互作用。为研究牛肉在冰箱冷冻室内冻结过程温度分布情况,首先用CAD建立了冰箱冷冻室以及牛肉的几何模型,并在Gambit中完成网格的划分,最后将网格文件导入到Fluent 15.0,在Fluent 15.0中进行参数设置与模拟计算。首先按上述设定好边界条件,选择k-ε计算模型,由于牛肉在冻结过程中存在温度的变化,因而需要激活能量项,其中,能量项的松弛因子按默认值设置,能量方程的收敛精度取10-6,激活重力选项,在Z轴方向,设重力加速度为-9.81 m/s2。其次牛肉在冰箱的冻结属于三维隐式非稳态模型,将牛肉的物性参数(密度、比热容、导热系数)调用到Fluent 15.0,并采用有限体积法离散控制方程。最后设置初始条件,分别给予牛肉初温以及冰箱冷冻室内环境温度,初始化流场后进行计算,时间步长取5 s,为了获取牛肉冻结时间,对牛肉体最大温度进行监测,实时导出牛肉体最大温度,结果表明18 060 s时牛肉内部最高温度低于-18 ℃,模拟结束,牛肉体最高温度分布曲线见图3。
为了清晰地看出牛肉内部冻结的温度分布情况,截取垂直于XOY的5个截面(图4),截面X分别为0.00,0.02,0.04,-0.01,-0.03 m。

图3 牛肉体最高温度分布曲线
由图4、5可知:牛肉底部换热最快,温度降低得最快,而牛肉顶部和侧面降温略慢,这是因为在冻结过程中,食品底部直接与蒸发盘管接触,存在接触导热作用,导热的热阻远小于对流换热的热阻,而且蒸发盘管的温度要低于冷冻室内部环境的温度,所以食品底部的温度下降较快。
2 牛肉冻结过程中试验研究与结果分析
2.1 试验研究
选取新鲜牛肉,准确切取100 mm×100 mm×70 mm规则的长方体形状,用标定好的美国OMEGA四氟测温线TT-T-36型热电偶温度探头固定好测点位置,置于恒温恒湿箱保存2 d,使牛肉获得初温(5 ℃)。然后选取试验测点(见图6)。试验前将冰箱空载运行1 d,保证冰箱冻结室内温度恒定。最后将固定好热电偶的牛肉,按照纤维方向与蒸发盘管平行的方式迅速置于冰箱冷冻室中间位置,并关好冰箱。打开计算机采集程序,每隔30 s用美国Fluke 2640A网络型多点温度采集仪记录一次数据,将采集的温度数据以Excel形式保存在电脑。
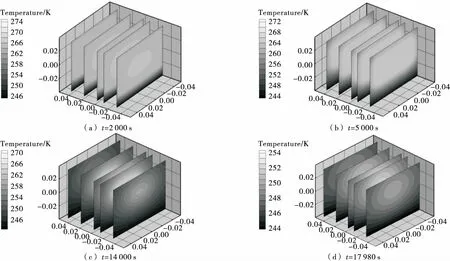
图4 不同时刻牛肉内部各截面的温度分布云图

图5 牛肉垂直中心截面位置不同时刻牛温度分布云图

T1热电偶固定在据牛肉上表面15 mm处,T2热电偶固定在几何中心偏右25 mm处,T3热电偶固定在牛肉的几何中心处,T4热电偶固定在据牛肉上表面45 mm处,T5热电偶固定在据牛肉下表面15 mm处牛肉的初始温度为5 ℃,冰箱冷冻室内部的空气温度为-29 ℃,底部蒸发盘管的温度为-30.4 ℃。图7是食品中心切面各测点试验值,由牛肉的冻结曲线可知:牛肉底部T4温度下降最快,而牛肉偏顶部T1温度下降最慢,冻结的时间最长,而牛肉的几何中心T3并非热中心,冻结时间相比T1短,由此可知冰箱冻结形状规则的长方体食品时,热中心在食品几何中心的上方。T5没有明显的相变期,可能是牛肉直接放置于蒸发盘管上,牛肉的下表面与蒸发盘管的温差较大,导致相变过程不明显。同一高度上测点T2比测点T3冻结速度快、冻结时间短,是因为T2受侧面对流换热和底部导热的相互作用明显。从各点试验值的温度曲线可知:冻结过程中,食品内部各测量点从某一时间点开始,持续一段时间,温度上下波动不明显,是由于从该时间点开始发生了相变过程释放大量的潜热,也可以看出食品冻结过程中相变发生在一定的温度范围内,从图7中可以看出,相变区间在-1.0~-2.6 ℃,而在相变之前和相变之后,食品的温度下降较快。
图6 试验取点示意图(cm)
Figure 6 Experimental take diagram

图7 食品中心切面各测点试验值
2.2 模拟结果与试验结果的对比分析
对照牛肉在冻结过程中模拟与试验的温度曲线可以看出,CFD技术能较好地模拟食品冻结过程中食品内部各部分温度的变化。冻结阶段牛肉的温度无明显变化,是因为在此阶段发生了相变,相变潜热的释放,使得模拟过程中表现为温度变化不明显。而冻结结束后,温度再次快速下降。
由图8(a)~(c)可知,预冷阶段模拟值与试验值存在差异,可能是冰箱冷冻式内部环境温度波动较大,使得对环境温度的测量与实际存在误差,而数值计算带入的环境温度是定值,进而使计算出的模拟值与试验值存在偏差。其次在相变阶段,模拟值温度恒定,而试验值略微下降,主要是因为试验过程中,随着食品的冻结,食品内部水结成冰,溶液的浓度增加,相变温度下降,而模拟时,假设相变温度是一个固定值,故存在差异。另外在相变阶段结束后模拟值与试验值温度偏差较大,可能是设置的牛肉热物性多项式与实际情况存在一定的差异,模拟时相变阶段牛肉的比热容设置比实际偏大,因而造成模拟的相变阶段时间会更长。
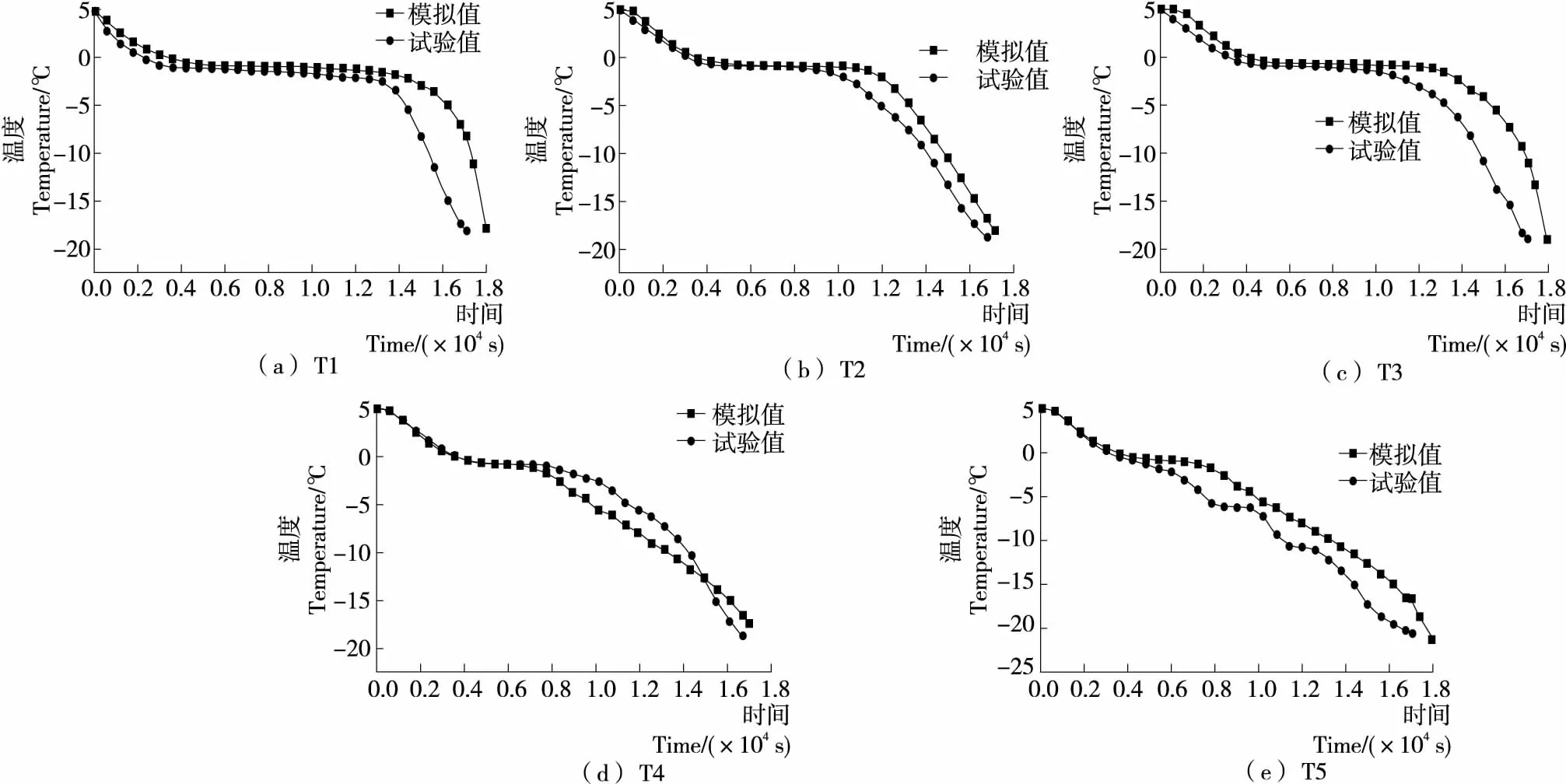
图8 牛肉内部各测点温度的试验值与模拟值的对比
由图8(d)可知,相变之前试验值和模拟值吻合较好,而相变结束后,模拟值与试验值出现了交叉,但总体来看牛肉模拟值围绕试验值附近波动。由图8(e)可以看出,冻结后的模拟值与试验值存在差异,试验值温度呈阶梯状下降,而模拟值温度呈单调递减趋势,可能是牛肉冻结后,模拟时设置的导热系数与实际存在偏差。模拟时冻结后导热系数的设置低于实际情况,可能是冰箱内部环境温度波动等造成的。总之,各测点模拟值能较好反映实际值,各测点(T1、T2、T3、T4、T5)模拟计算的冻结时间与试验冻结时间的误差分别为5.45%,3.90%,5.80%,4.24%,9.60%,各点实时温度的模拟平均误差为1.79 ℃。
3 结论
本试验采用等效热容法处理相变潜热,建立描述三维食品冻结过程的微分方程,通过CFD数值模拟技术对冰箱冷冻室内牛肉的冻结过程进行了计算,从模拟所得的温度云图能直观地观察出牛肉内部的热中心并非几何中心,而是几何中心偏上14 mm处,并对冻结过程进行了验证。试验表明数值模拟能很好地反映牛肉内部温度场的变化,各测点(T1、T2、T3、T4、T5)模拟计算的冻结时间与试验冻结时间的误差控制在±10%,各点实时温度的模拟平均误差为1.79 ℃。该研究表明CFD可以较好地用于预测食品冻结时间,而冻结时间既是衡量冻结设备优劣的重要标准,也是评价冻结食品品质的影响因素之一,因此本研究为研发和优化冻结设备的性能、降低能耗以及提高食品品质提供了一种可靠的理论方法。
[1] 张珍, 谢晶, 李杰. 计算流体力学在制冷设备研发中的应用[J]. 食品与机械, 2008, 24(2): 146-150.
[2] 王金锋, 李文俊, 谢晶. 数值模拟在食品冻结过程中的应用[J]. 食品与机械, 2016, 32(10): 200-204.
[3] 周小清, 柳建华, 徐小进, 等. 液氮冻结食品冻结时间的计算方法及实验验证[J]. 制冷学报, 2016, 37(6): 113-118.
[4] PHAM Q T. Freezing time formulas for foods with low moisture content, low freezing point and for cryogenic freezing[J]. Journal of Food Engineering, 2014, 127(4): 85-92.
[5] BECKER B R, FRICKE B A. Freezing times of regularly shaped food items[J]. International Communications in Heat & Mass Transfer, 1999, 26(5): 617-626.
[6] 李杰, 谢晶. 鼓风冻结虾仁时间的数值模拟及实验验证[J]. 农业工程学报, 2009, 25(4): 248-252.
[7] 李杰, 谢晶, 陆方娟. 食品冻结过程温度场及冻结时间的数值模拟与实验研究[J]. 食品工业科技, 2009, 30(2): 123-125, 128.
[8] 屠建祥, 刘宝林. 黄瓜片冻结过程的数值计算及实验研究[J]. 上海理工大学学报, 2000, 22(4): 304-307.
[9] 谢晶, 施骏业, 瞿晓华. 食品热物性的多项式数学模型[J]. 制冷, 2004, 23(4): 6-10.
[10] PHAM Q T. Modelling heat and mass transfer in frozen foods: a review[J]. International Journal of Refrigeration, 2006, 29(6): 876-888.
[11] 李晓宇, 刘斌, 邸倩倩, 等. 马铃薯冻结过程中不同风速对相变界面的影响[J]. 食品科技, 2015(4): 76-81.
[12] WANG Zheng-fu, WU Han, ZHAO Guang-hua, et al. One-dimensional finite-difference modeling on temperature history and freezing time of individual food[J]. Journal of Food Engineering, 2007, 79(2): 502-510.
[13] 殷刚. 平板状食品冻结时间的数值计算[J]. 哈尔滨商业大学学报: 自然科学版, 2006, 22(5): 99-101.
[14] UYAR R, BEDANE T F, ERDOGDU F, et al. Radiofrequ-ency thawing of food products: A computational study[J]. Journal of Food Engineering, 2015, 146: 163-171.
[15] 王石, 田怀璋, 陈林辉, 等. 冰箱试验包传热过程的仿真计算[J]. 西安交通大学学报, 2005, 39(1): 57-60.
[16] MORGAN V T. The Overall Convective Heat Transfer from Smooth Circular Cylinders[J]. Advances in Heat Transfer, 1975, 11: 199-264.
Stimulation and theoretical analysis of heat transfer during the freezing process simulation of beef
TANGWan1,2
WANGJin-feng1,2
LIWen-jun1,2
XIEJing1,2
(1.ShanghaiEngineeringResearchCenterofAquaticProductProcessing&Preservation,Shanghai201306,China; 2.CollegeofFoodScienceandTechnology,ShanghaiOceanUniversity,Shanghai201306,China)
Freezing is recognized as one of the important technology in food preservation. Considering the change of physical characteristics in beef under the process of the freezing, the equivalent heat capacity method was utilized to process latent heat in phase change, and then the computational fluid dynamics (CFD) numerical simulation technology was applied to simulate the freezing process and establish the differential equations of three dimensional food freezing process. Through the numerical simulation of freezing time, the error between each experimental measuring point (T1, T2, T3, T4 and T5) value and simulation calculation of freezing time were detected to be 5.45%, 3.9%, 5.8%, 4.24%, 5.8%, respectively, and each point temperature real-time simulation of the average error was 1.79 ℃. The results showed that the numerical simulation could predict the beef to freeze time well.
numerical simulation; freezing time; food freezing; refrigerator
国家“十三五”重点研发项目(编号:2016YFD0400303);上海市科委平台能力提升项目(编号:16DZ2280300)
唐婉,女,上海海洋大学在读硕士研究生。
谢晶(1968—),女,上海海洋大学教授,博士生导师,博士。E-mail: jxie@shou.edu.cn
2017—05—09
10.13652/j.issn.1003-5788.2017.07.027

