风攻角对分离双扁平箱梁涡振特性的影响
, , ,
(1.石家庄铁道大学 大型结构健康诊断与控制研究所,河北 石家庄 050043;2.石家庄铁道大学 土木工程学院,河北 石家庄 050043;3.河北省大型结构健康诊断与控制重点实验室,河北 石家庄 050043)
风攻角对分离双扁平箱梁涡振特性的影响
刘小兵1,3,陈帅2,张海东2,张胜斌2
(1.石家庄铁道大学 大型结构健康诊断与控制研究所,河北 石家庄 050043;2.石家庄铁道大学 土木工程学院,河北 石家庄 050043;3.河北省大型结构健康诊断与控制重点实验室,河北 石家庄 050043)
在均匀流场中进行了分离双扁平箱梁涡激振动节段模型风洞试验,研究了-5° ~ +5° 间8个不同风攻角下分离双箱梁在D/B=0.1(D为双箱梁的净间距,B为单箱梁的宽度)时的涡振特性,并将结果与单箱梁的结果进行了对比。结果显示:+5°风攻角下,上下游箱梁的涡激振动受到了抑制,表现为振幅的减小和风速锁定区间的缩短;随着风攻角的逐渐变小,这种抑制效应逐渐变弱,并转变为放大效应; +2°风攻角下,单箱梁未发生涡激振动现象,但上下游箱梁均发生了比较明显的涡激振动。
涡激振动;分离双箱梁;风攻角;风洞试验
0 引言
随着近年来交通流量的不断增大,现代桥梁常采用上下行分离的双箱梁结构,如连接上海崇明区和江苏省启东市的崇启大桥、广东佛山平胜大桥、青岛海湾大桥红岛航道桥等等。这类桥的分离双箱梁一般具有相同的外形、质量及频率特性。由于主梁的阻尼小,且两分离箱梁之间存在气动干扰问题,导致这类桥比较容易发生涡激振动。
由于气动干扰效应的影响,与单箱梁相比,分离双箱梁在某些特定间距和风攻角下的涡振特性可能会变差。针对分离双箱梁的涡激振动问题,已有一些研究者开展了相关研究工作。Kimura 采用节段模型风洞试验的手段研究了不同间距时某分离双箱梁桥的涡振特性[1],研究结果表明:双箱梁涡激振动的干扰效应很显著,即使当双箱梁的净间距为8倍的单箱梁宽时,这种干扰效应仍不可忽略。陈政清等针对佛山平胜桥进行了涡激振动风洞试验[2],试验发现,随着间距的增大,双箱梁涡激振动的气动干扰效应逐渐减弱,当D/B≥0.8(D为双箱梁的净间距,B为单箱梁的宽度)时气动干扰的影响已经很小。刘志文等针对串列双流线型箱梁断面开展了节段模型涡激振动试验研究[3],研究发现:气动干扰对上游箱梁涡激振动的影响在D/B≤3时表现为增大效应,在D/B>3 时影响很小; 下游箱梁的涡激振动主要受上游箱梁涡振振幅的影响。朱乐东等通过风洞试验研究了气动干扰对某分离双箱梁桥涡振特性的影响,试验风攻角为0°、-3°和+3°[4],研究结果表明:气动干扰效应与来流风攻角有关,+3°风攻角时,气动干扰效应最显著,0°风攻角的干扰效应次之,-3°风攻角的干扰效应最小。廖海黎等基于全桥气弹模型风洞试验研究了崇启大桥分离双钢箱梁的涡振特性[5],研究发现:双箱梁的涡激振动存在两个涡振区;前一涡振区对应于上风侧主梁涡激响应,下风侧主梁为上风侧主梁涡激响应引起的共振,两侧主梁涡激振幅相当;后一涡振区为下风侧主梁涡激响应,引起上风侧主梁共振,下风侧主梁涡激振幅强于上风侧主梁。
综合以上文献可以发现,间距和风攻角是分离双箱梁涡振特性的两个主要影响因素。目前的相关研究侧重分析分离双箱梁的涡振特性随间距的变化规律,风攻角对分离双箱梁涡振特性的影响研究较少。本文以某座分离双扁平箱梁桥为背景,开展了一系列的节段模型风洞试验,详细研究了-5° ~ +5°间8个不同风攻角下分离双箱梁的涡振特性,并将结果与单箱梁的结果进行了对比,探讨了风攻角对分离双箱梁涡激振动的影响。
1 风洞试验概况
某分离双箱梁桥设计方案由相邻的两幅斜拉桥共同组成,单幅主梁采用扁平封闭钢箱加劲梁,梁宽为18.5m,梁高为3.2m。以该桥为工程背景,按1∶50的几何缩尺比设计的风洞试验模型如图1所示。单箱梁模型宽B=370mm,高H=64mm,长L=2 000mm,双箱梁模型之间的净间距为D。在本试验中,双箱梁模型的净间距D与单箱梁模型宽B之比D/B为0.1。

图1 双箱梁模型的几何参数(单位:mm)
试验在石家庄铁道大学大气边界层风洞低速试验段中进行,试验流场为均匀流场。试验装置和试验照片如图2和图3所示,上下游箱梁模型分别通过8根弹簧悬挂。风洞试验过程中模型振动引起的弹簧张力时程通过力传感器测得。根据弹簧的张力时程和预先标定好的弹簧刚度,由胡克定律可以得到模型的振动位移时程。表1列出了模型的试验参数。两箱梁模型的质量、频率及阻尼比等基本保持一致。
分别针对单箱梁模型和分离双箱梁模型进行了涡激振动测试,来流风攻角分别为+5°、+4°、+3°、+2°、+1°、0°、-3°和-5°。定义斜向上吹向模型的来流风为正攻角来流风,斜向下吹向模型的来流风为负攻角来流风。试验的风速范围为2.7~13.8 m/s。

表1 分离双箱梁模型的试验参数
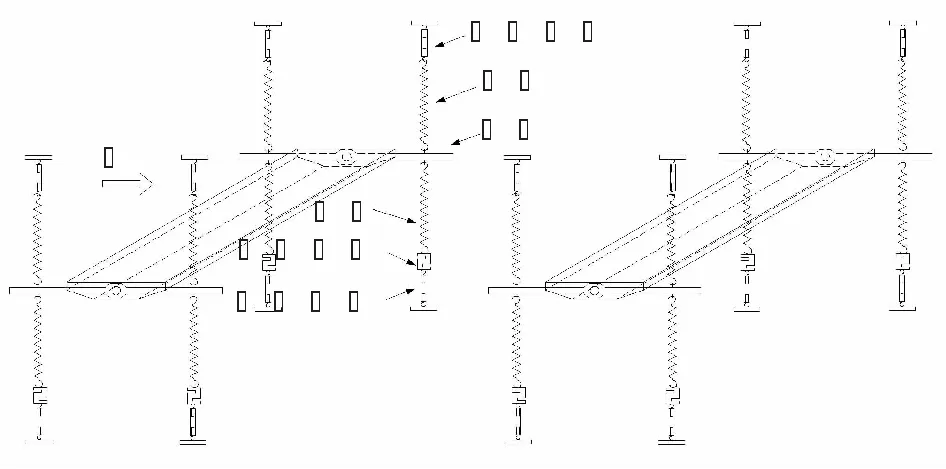
图2 风洞试验装置示意

图3 风洞试验照片
2 风洞试验结果分析
风洞试验发现:在测试的风速范围内,-5°~ +5°之间各风攻角下单箱梁模型及分离双箱梁模型均没有发生明显的扭转涡激振动现象。
在+5°、+4°和+3°风攻角下,单箱梁模型发生了竖弯涡激振动现象。图4为+5°风攻角,风速为5.5 m/s时单箱梁模型的竖向位移时程及幅值谱。需要特别说明的是,本文中给出的所有位移(或振幅)均为试验模型的位移(或振幅),风速均为风洞试验风速。从图4(a)可以发现,单箱梁的振动为类谐波振动。从图4(b)可见两个卓越频率,其中较大幅值对应的频率与单箱梁的固有竖向频率非常接近,约为5.76 Hz。较小幅值对应的频率约为单箱梁固有竖向频率的2倍。

图4 单箱梁的竖向位移时程及幅值谱(风攻角+5°V=5.5 m/s)

图5 单幅箱梁的竖向振幅随风速的变化曲线
图5为单箱梁在8个不同风攻角下的竖向振幅随风速的变化曲线。可以看到, +5°风攻角时涡激振动的风速锁定区间为3.6~5.7 m/s,在5.5 m/s左右的风速下振幅最大。随着风攻角的逐渐减小,单箱梁涡激振动的振幅逐渐变小,风速锁定区间逐渐变短。这说明单箱梁的涡激振动性能随着风攻角的减小逐渐变好。
风攻角为+5°、+4°、+3°和+2°时,分离双箱梁模型发生了比较明显的竖弯涡激振动现象。图6显示了风攻角为+5°,风速V=3.6 m/s时上下游箱梁的竖向位移时程及幅值谱。限于篇幅,其它风攻角下的竖向位移时程及幅值谱没有给出。从图6(a)可以看到,上下游箱梁的振动虽然均为类谐波振动。但振动并不同步。从图6(b)可以发现,上下游箱梁均可见两卓越频率,其中较大幅值对应的频率与单箱梁的固有竖向频率非常接近,较小幅值对应的频率约为单箱梁固有竖向频率的2倍。
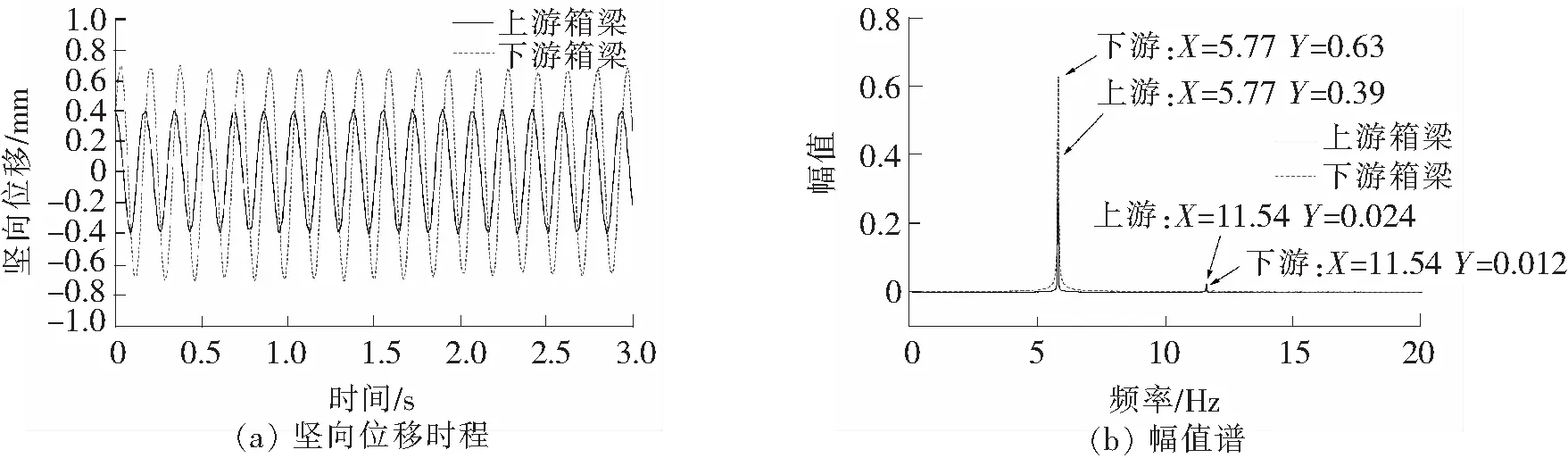
图6 分离双箱梁的竖向位移时程及幅值谱(风攻角+5°V=3.6 m/s)
图7所示为不同攻角上游箱梁与下游箱梁的竖向振幅随风速的变化曲线。
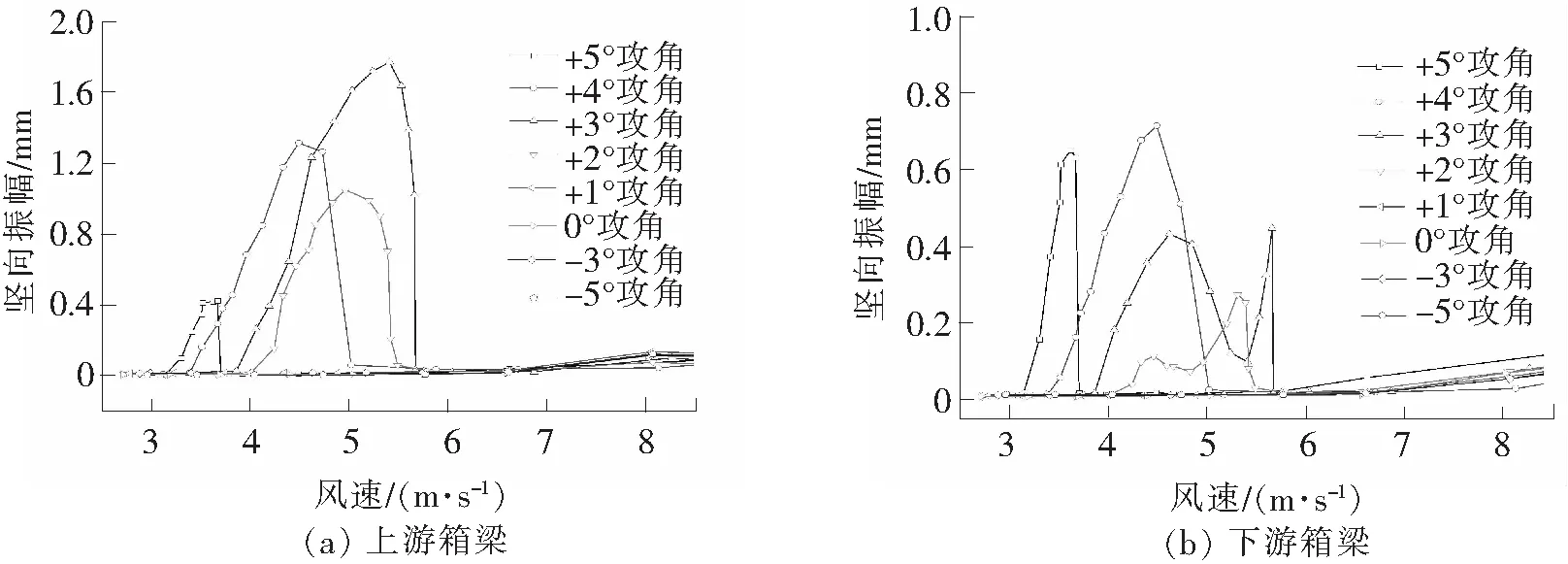
图7 不同攻角时上下游箱梁的竖向振幅随风速的变化曲线
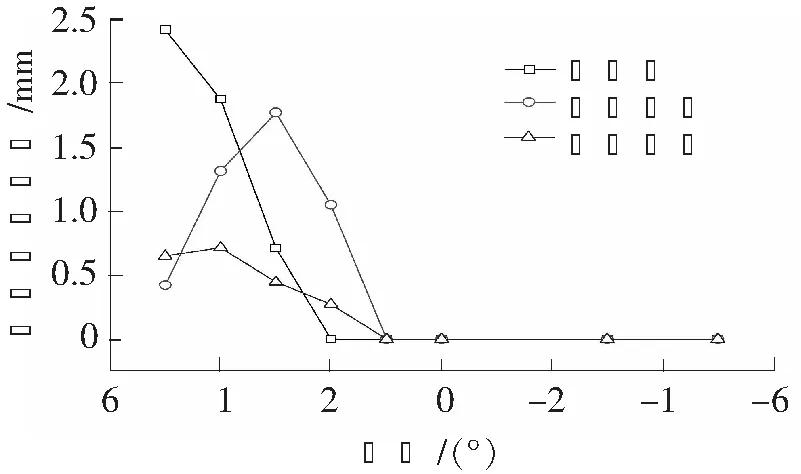
图8 上下游箱梁最大振幅随风攻角的变化曲线
图8所示为上游箱梁和下游箱梁的最大竖向振幅随风攻角的变化曲线,并与单箱梁的最大竖向振幅进行了对比。表2列出了不同风攻角下双箱梁的涡振风速锁定区间及长度,并与单箱梁的结果进行了对比。
综合图7、图8和表2可以发现:
(1)+5°风攻角下,上下游箱梁的最大振幅值均小于单箱梁的最大振幅值,风速锁定区间长度均比单箱梁的风速锁定区间长度短。这表明,在此风攻角下,双箱梁的涡激振动受到了一定的抑制作用。
(2)+4°风攻角下,上下游箱梁的最大振幅值均小于单箱梁的最大振幅值,风速锁定区间长度均比单箱梁的风速锁定区间长度短,但与+5°风攻角的结果相比,+4°风攻角下的这种差异相对较小。这表明,在+4°风攻角下,双箱梁的涡激振动仍受到抑制,只不过这种抑制效应变弱了。
(3)+3°风攻角下,上游箱梁的最大振幅值大于单箱梁的最大振幅值,下游箱梁的最大振幅值虽然仍小于单箱梁的最大振幅值,但与+5°和+4°风攻角相比,这种差异进一步变小。这说明,随着风攻角的进一步减小,双箱梁涡激振动的抑制效应进一步减小,并逐渐转变为放大效应。
(4)+2°风攻角下,单箱梁未发生涡激振动现象,但上下游箱梁均发生了比较明显的涡激振动现象。这表明,与+3°风攻角相比,双箱梁涡激振动的放大效应得到了加强。
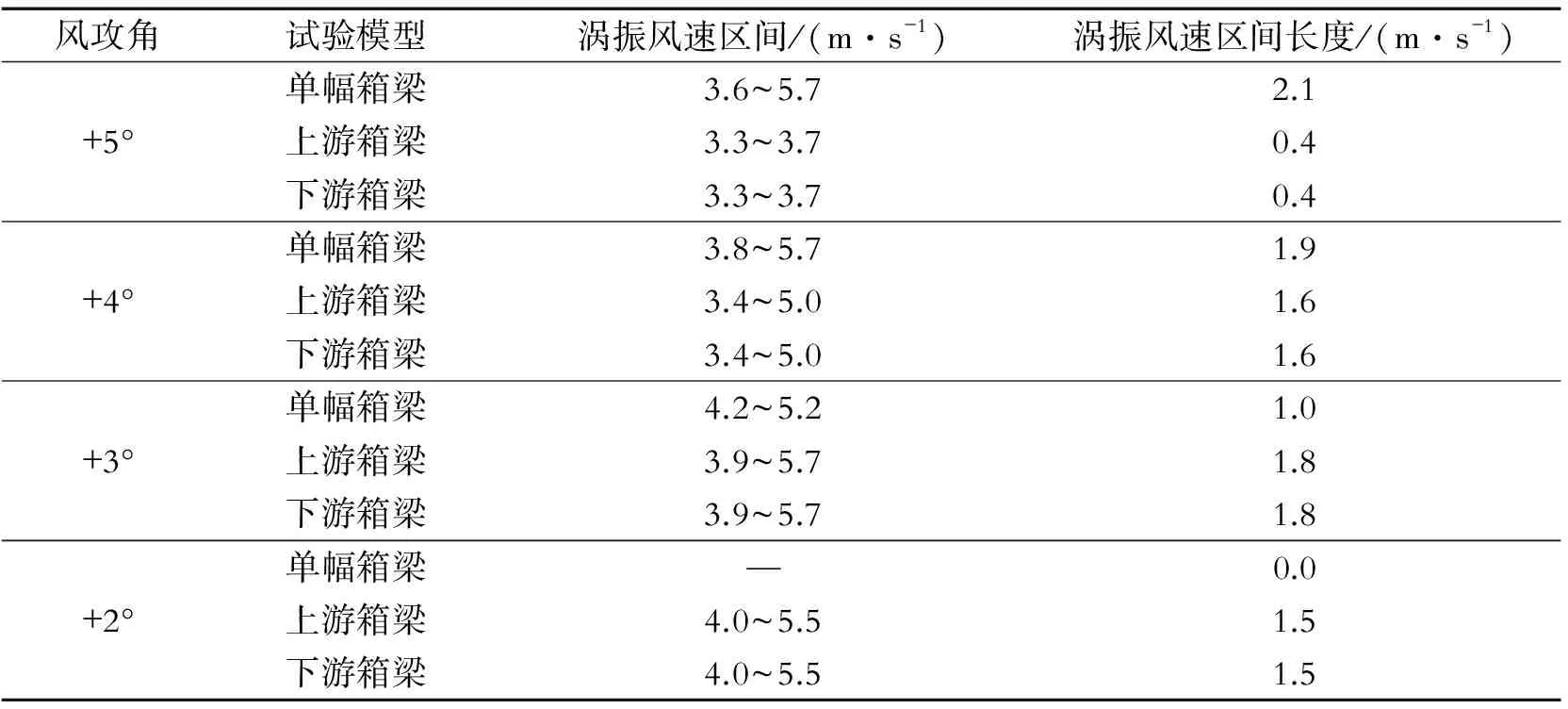
表2 不同攻角下单箱梁与双箱梁涡振风速锁定区间及长度
在D/B=0.1左右的较小间距时,上游箱梁背风面和下游箱梁迎风面之间的风效应可能类似于与双圆(方)柱的临界间距效应[6-7]。当两箱梁的间距小于临界间距时,下游箱梁的存在会对上游箱梁尾部的旋涡脱落产生一定的抑制作用;当两箱梁的间距大于临界间距时,下游箱梁的存在会对上游箱梁尾部的旋涡脱落产生一定的放大作用。在+5°风攻角下,双箱梁的临界间距可能大于0.1倍的单箱梁宽,因而,其涡振受到抑制作用。随着风攻角的变小,双箱梁的临界间距可能逐渐变小,并小于0.1倍的单箱梁宽,因而,随着风攻角的变小,这种抑制效应逐渐变弱,并最终转变为放大效应。
3 结论
基于节段模型风洞试验研究了-5° ~ +5°间不同风攻角下单幅扁平箱梁的涡振特性及分离双扁平箱梁在D/B=0.1(D为双箱梁的净间距,B为单箱梁的宽度)时的涡振特性,主要得到了两点结论:
(1)单箱梁在+5°风攻角时的涡振振幅最大,风速锁定区间最长。随着风攻角的减小,单箱梁的涡激振动性能逐渐变好。
(2)双箱梁的涡振特性与来流风攻角密切相关,在+5°风攻角下,上下游箱梁的涡激振动受到抑制,表现为振幅的减小和风速锁定区间的缩短;随着风攻角的逐渐变小,这种抑制效应逐渐减弱,并转变为放大效应。
本文仅在D/B=0.1这种特定的间距下研究了风攻角对分离双扁平箱梁涡振特性的影响。为了全面深入掌握风攻角对分离双扁平箱梁涡振特性的影响规律,在后续的研究中,将在多个不同的间距下开展研究工作。
[1]Kimura K, Shima K, Sano K, et al. Effects of seperation distance on wind-induced response of parallel box girders[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96: 954-962.
[2]陈政清, 牛华伟, 李春光. 并列双箱梁桥面风致涡激振动试验研究[J]. 湖南大学学报, 2008, 35(1): 16-20.
[3]刘志文, 陈政清, 栗小祜,等. 串列双流线型断面涡激振动气动干扰试验[J]. 中国公路学报, 2011, 24(3): 51-57.
[4]朱乐东, 周奇, 郭震山,等. 箱形双幅桥气动干扰效应对颤振和涡振的影响[J]. 同济大学学报, 2010, 38(5): 632-638.
[5] 秦浩, 廖海黎, 李明水. 大跨度双幅连续钢箱梁桥涡激振动特性风洞试验研究[J]. 振动与冲击, 2014, 33(14): 206-210.
[6]D.Sumner.Two circular cylinders in cross-flow: A review [J].Journal of Fluids and Structures,2010, 26: 849-899.
[7]陈素琴, 黄自萍, 沈剑华,等. 两串列方柱绕流的干扰数值研究[J]. 同济大学学报, 2001, 29 (3) : 320-325.
EffectofWindAttackingAngleonVortexInducedVibrationCharacteristicsofTwinSeparateFlatBoxGirders
LiuXiaobing1,3,ChenShuai2,ZhangHaidong2,ZhangShengbin2
(1. Structural Health Monitoring and Control Institute, Shijiazhuang TieDao University, Shijiazhuang 050043, China;2. School of Civil Engineering, Shijiazhuang TieDao University, Shijiazhuang 050043, China;3. Key Lab of Structural Health Monitoring and Control of Hebei Province, Shijiazhuang 050043, China)
Sectional model wind tunnel tests are carried out in the uniform flow field for twin separate flat box girders underD/B=0.1 (Dis net distance of twin separate flat box girders andBis width of single flat box girder) and wind attacking angle ranging from -5° to +5°. Vortex induced vibration characteristics of twin separate flat box girders are studied and compared with that of single box girder. The results show that when the wind attacking angle is +5°, the vibration amplitude and wind speed range of both upstream and downstream flat box girders are smaller than those of single flat box girder. With decreasing of wind attacking angle, this suppression effect becomes weak and changes to amplification effect gradually. When the wind attacking angle is +2°, no vortex induced vibration occurs for single box girder, while comparatively large vortex induced vibrations is observed for twin box girders.
vortex induced vibration;twin separate box girders;wind attacking angle;wind tunnel test
TU311.3
: A
: 2095-0373(2017)03-0001-05
2016-09-26责任编辑:刘宪福
10.13319/j.cnki.sjztddxxbzrb.2017.03.01
国家自然科学基金(51308359);河北省高等学校科学技术研究基金(QN20131169,QN2015213)
刘小兵(1982-),男,副教授,主要从事桥梁结构抗风研究。E-mail:x_b_liu@126.com 刘小兵,陈帅,张海东,等.风攻角对分离双扁平箱梁涡振特性的影响[J].石家庄铁道大学学报:自然科学版,2017,30(3):1-5.

