基于模糊熵和包络分析的滚动轴承故障特征提取

, ,

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

基于模糊熵和包络分析的滚动轴承故障特征提取

郭学卫,申永军,杨绍普

(石家庄铁道大学 机械工程学院，河北 石家庄 050043)

提出了一种基于模糊熵和包络分析的故障特征提取新方法。这种方法的核心是首先使用包络分析把调制的振动信号进行解调，然后计算并比较这些包络信号的模糊熵，从而实现故障的特征提取。研究表明，用这种方法提取信号特征，可以容易地将正常滚动轴承、内圈故障、外圈故障和滚子故障的信号区分。

模糊熵；包络分析；Hilbert变换；特征提取

0 引言

在机械设备故障诊断中，如何有效提取故障特征信息是故障诊断的关键。近年来，随着各种非线性动力学理论的发展，如分形维数、混沌特征参量、近似熵等方法已被广泛地应用于机械故障诊断领域[1-2]，并取得了不错的成果。2007年，陈伟婷等人对样本熵算法进行了改进，首次提出了模糊熵的概念[3]，并成功应用于体表肌电信号的特征提取与分类。对于滚动轴承振动信号，不同故障的振动信号的复杂性不同，因而其对应的模糊熵值也不同。因此，模糊熵可以对滚动轴承故障特征进行提取。但大量文献[4-5]研究表明如果直接使用原始信号的模糊熵进行特征提取，无法对各故障模式实现有效区分。这是因为原始信号的模糊熵所提供的信息有限，不能反映轴承损伤情况的深层次信息，因而不足以对轴承的所有工况进行区分。同时这也是因为当滚动轴承出现故障时，信号中包含的故障信息往往都是以调制形式出现的，若直接对调制信号进行分析，不利于故障的诊断和识别[6-7]。尤其是当故障处于早期状态或因故障导致的冲击信号不明显时，更难以从调制信号中获得有用的故障特征。包络分析作为信号解调的一种方法，它可以把与故障有关的信号从高频调制信号中解调出来，避免与其他低频干扰信号的混淆，从而有效提高诊断结果的可靠性。

基于上文的描述，提出了一种基于模糊熵和包络分析的故障特征提取新方法。该方法的步骤首先使用包络分析把调制的振动信号进行解调，然后计算并比较这些包络信号的模糊熵，从而实现故障的特征提取。为了说明这种方法的有效性，本文采用凯斯西储大学(Case Western Reserve University,简称CWRU)电气实验室轴承数据中心提供的滚动轴承数据进行分析。研究发现，用包络信号的模糊熵提取信号特征，可以容易地将正常滚动轴承、内圈故障、外圈故障和滚子故障的信号区分。

1 模糊熵

1.1模糊熵的定义

近似熵和样本熵的定义可参见文献[8-9]。在近似熵和样本熵中，两个向量的相似性度量都是基于阶跃函数定义的，而阶跃函数的突变性使得熵值缺乏连续性。模糊熵的定义则借用了模糊函数的概念，并选择指数函数作为模糊函数来测度两个向量的相似性。指数函数具有以下特性：(1)连续性,保证其值不会产生突变；(2)凸性质,保证向量自身的自相似性值最大。因此，与近似熵和样本熵相比，模糊熵算法用指数函数模糊化相似性度量公式,模糊熵值随参数变化连续且平稳。其次，模糊熵通过去均值运算，除去了基线漂移的影响，且向量的相似性不再由绝对幅值差确定，而由指数函数确定的模糊函数确定，从而将相似性度量模糊化，改善了分类效果。

模糊熵的定义如下[3]：

(1)对N点时间序列{u(i):1≤i≤N}按顺序重构生成一组m维向量

(1)

(2)

(3)

(4)

(4)定义函数

(5)

(5)类似的，再对维数m+1，重复上述(1)～(4)，得

(6)

(6)定义模糊熵

(7)

当N为有限数时，式(7)表示成

(8)

1.2参数的选取

由模糊熵的定义，模糊熵的计算和嵌入维数m、模糊函数边界的宽度r、梯度n、数据长度N都有关系。(1)嵌入维数m的选取。同近似熵、样本熵一样，一般取嵌入维数m=2。因为在时间序列进行重构时，m越大，就会有越多的信息，但m越大，计算所需要的数据长度就更长(N=10m～30m)，因此综合考虑，取m=2。(2)r的选取。r表示模糊函数边界的宽度。r过大会造成信号中原始信息的大量丢失；r过小得到的统计特性的效果则不理想，而且熵值会受到噪声的显著影响。一般r取0.1～0.25SD(SD是原始数据的标准差)，本文取r=0.15SD。(3)n的选取。n是模糊函数边界的梯度，n越大则梯度越大。n过大会导致信息的丧失，而且计算量也会增大。为了获得尽量多的信息，文献[3]建议计算时取较小的整数值，如2或3等。综上考虑，本文取n=2。(4)数据长度N的选取。模糊熵值的结果对数据的长度要求不高，若选定m=2，则N=100～900[4]。

2 包络分析

2.1希尔伯特变换

希尔伯特变换是一种线性变换，也就是在同一域中把一个函数映射为另一个函数。它的重要意义在于揭示了可实现的系统函数实部和虚部之间的相互关系。运用Hilbert变换对信号进行包络解调，可以把故障信号从高频调制信号中解调出来，避免了与其他低频干扰信号的混淆，该解调方法简单有效，因此在机械设备故障诊断中应用较多[10]。

(9)

(10)

(11)

2.2包络解调

滚动轴承发生故障时所测得的振动信号通常是调制信号，文献[6-7]研究表明，若直接对调制信号进行分析，不利于故障的诊断和识别。尤其是当滚动轴承故障处于早期状态或因故障导致的冲击信号不明显时，更是难以从调制信号中获得有用的故障特征。包络分析作为信号解调的一种主要方法，能将轴承的故障信息从复杂的调制信号中分离出来，可以挖掘信号中更深层次的信息，获得更加明显的故障特征，从而有效提高诊断结果的可靠性。

3 故障特征提取方法及实例

基于上文的描述，可以建立基于模糊熵和包络分析的故障特征提取新方法。本文将模糊熵和包络分析相结合,提取滚动轴承故障信息具体方法如下。

考虑到直接从传感器获取的振动信息包含了大量的干扰噪声，将对后续分析产生很大的影响，不利于故障特征的提取[11-12]，因此采用小波阈值法对采集的振动信号进行降噪处理，以减少噪声的干扰。因此，首先采用小波阈值法对采集的振动信号进行降噪处理，其中小波基选择DB9。然后对经过小波降噪后的振动信号x(t)进行零均值化处理,并实施Hilbert变换,得到信号的解析信号

(12)

式中，H[(t)]即为x(t)的Hilbert变换，x(t)的包络信号为

(13)

最后计算Z(t)的模糊熵。

为了说明这种方法的有效性，将其应用到滚动轴承故障特征提取中。实验数据由凯斯西储大学(Case Western Reserve University，简称CWRU)电气实验室轴承数据中心提供，滚动轴承的型号为SKF6205。本文数据选择电机旋转速度为1 772 r/min，采样频率为12 kHz的正常轴承、内圈故障、外圈故障和滚动体故障4种工况下的振动数据，故障深度为0.355 6 mm。实验结果如图1、图2所示，线1至线4分别为外圈故障、正常轴承、内圈故障和滚动体故障各24组未经包络的振动信号和经过包络的振动信号的模糊熵计算结果。

图1 小波降噪后信号的模糊熵

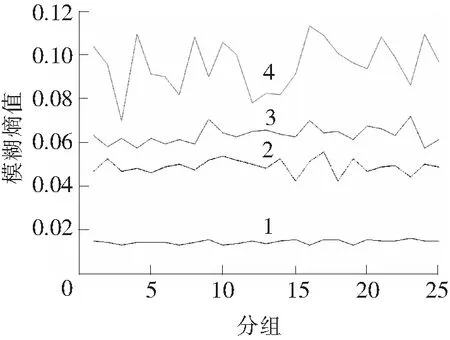
图2 小波降噪后包络信号的模糊熵

由图1和图2可明显看出,未经包络的信号的模糊熵无法将正常轴承、内圈故障、外圈故障和滚动体故障的信号区分开,而包络信号的模糊熵可以容易的将四种状态的信号区分开来。

4 结论

本文对基于模糊熵和包络分析用于滚动轴承故障特征提取这种新方法进行了研究，以滚动轴承为对象,首先使用包络分析把复杂的调制振动信号进行解调，然后计算并比较这些包络信号的模糊熵，成功地将正常、内圈故障、外圈故障和滚动体故障信号进行了区分,效果十分显著。由此可知，把调制的轴承振动信号进行解调，再进行模糊熵特征提取，比直接对轴承振动信号进行模糊熵特征提取，可以挖掘信号中更深层次的信息，能得到更好的诊断效果。

[1]胥永刚, 何正嘉. 分形维数和近似熵用于度量信号复杂性的比较研究[J]. 振动与冲击, 2003, 22(3): 25-27.

[2]Yan R, Gao R X. Approximate entropy as a diagnostic tool for machine health monitoring[J]. Mechanical Systems and Signal Processing, 2007, 21(2): 824-839.

[3]陈伟婷. 基于熵的表面肌电信号特征提取研究[D].上海 上海交通大学生物医学工程学院, 2008.

[4]郑近德, 陈敏均, 程军圣, 等. 多尺度模糊熵及其在滚动轴承故障诊断中的应用[J]. 振动工程学报, 2014, 27(1): 145-151.

[5]刘慧, 谢洪波, 和卫星, 等. 基于模糊熵的脑电睡眠分期特征提取与分类[J]. 数据采集与处理, 2010, 25(4): 484-489.

[6]Shen Y, Yang S, Wang J. Application of Higher-Order Cumulant in Fault Diagnosis of Rolling Bearing[J].Journal of Physics: Conference Series. IOP Publishing, 2013, 448(1): 012008.

[7]张桂才, 史铁林. 基于高阶统计量的机械故障特征提取方法研究[J]. 华中理工大学学报, 1999, 27(3): 6-8.

[8]Pincus S M. Approximate entropy as a measure of system complexity[J]. Proceedings of the National Academy of Sciences, 1991, 88(6): 2297-2301.

[9]Richman J S, Moorman J R. Physiological time-series analysis using approximate entropy and sample entropy[J]. American Journal of Physiology-Heart and Circulatory Physiology, 2000, 278(6): H2039-H2049.

[10]于德介,程军圣. 故障诊断的Hilbert-Huang变换方法[M]. 北京: 科学出版社, 2006.

[11]申永军, 张光明, 祁玉玲, 等. 基于Gabor变换的自适应降噪方法[J]. 石家庄铁道大学学报: 自然科学版, 2010, 23(2): 69-73.

[12]张光明, 申永军, 吴彦彦. 基于Gabor变换的信号降噪方法[J]. 石家庄铁道学院学报: 自然科学版, 2009, 22(3): 86-90.

ApplicationofFuzzyEntropyandEnvelopeAnalysisinFaultDiagnosisofRollingBearing

GuoXuewei,ShenYongjun,YangShaopu

(Department of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043， China)

In this paper a new method of pattern recognition based on fuzzy entropy and envelope analysis is presented. The core of this new method is to demodulate vibration signal by envelope analysis firstly. Then the fuzzy entropy of the envelope signals are computed and compared. The study shows this new method could discriminate between the normal and the three fault signals distinctly.

fuzzy entropy;envelope analysis;Hilbert transform;feature extraction

TH17

： A

： 2095-0373(2017)03-0025-04

2016-03-29责任编辑:刘宪福

10.13319/j.cnki.sjztddxxbzrb.2017.03.05

国家自然科学基金(11372198)；河北省高等学校创新团队领军人才计划(LJRC018)；河北省高等学校高层次人才科学研究项目(GCC2014053)；河北省高层次人才资助项目(A201401001)

郭学卫(1991-)，男，硕士研究生，研究方向为故障诊断。E-mail:1607840744@qq.com

申永军(1973-),男，博士，教授，博士生导师，研究方向为机械系统的动力学分析与振动控制。E-mail:shenyongjun@126.com 郭学卫,申永军,杨绍普.基于模糊熵和包络分析的滚动轴承故障特征提取[J].石家庄铁道大学学报:自然科学版,2017,30(3):25-28.