基于改进遗传算法的餐厅服务机器人路径规划

徐 林，范昕炜

(中国计量大学 质量与安全工程学院，杭州 310018) (*通信作者电子邮箱792243200@qq.com)

基于改进遗传算法的餐厅服务机器人路径规划

徐 林*，范昕炜

(中国计量大学 质量与安全工程学院，杭州 310018) (*通信作者电子邮箱792243200@qq.com)

针对遗传算法(GA)易产生早熟现象和收敛速度慢的问题，提出了一种基于传统遗传算法(TGA)的改进遗传算法——HLGA，用于实际餐厅服务机器人的路径规划。首先，通过基于编辑距离的相似度方法对拟随机序列产生的初始种群进行优化；其次，采用自适应算法的改进交叉概率和变异概率调整公式，对选择操作后的个体进行交叉、变异操作；最后，计算具有安全性评价因子函数的个体适应度值，进一步对比、迭代得到全局最优解。理论分析和Matlab仿真表明，与TGA和基于个体相似度改进的自适应遗传算法(ISAGA)相比，HLGA的运行时间分别缩短了6.92 s和1.79 s，且规划的实际路径更具有安全性和平滑性。实验结果表明HLGA在实际应用中能有效提高路径规划质量，同时缩小搜索空间、减少规划时间。

遗传算法；餐厅服务机器人；拟随机序列；编辑距离；路径规划

0 引言

国际机器人联合会指出，服务机器人是一种半自主或全自主工作的机器人，它能够完成有益于人类健康的服务工作，但不包括从事生产的设备[1]。餐厅送餐机器人是服务机器人的一种。在此过程中,机器人以怎样的路线行进——路径规划(一种有目的性的自我移动技术)，已经成为该领域的核心技术和研究热点之一。它一般是指在某一具有障碍物的环境中寻找出移动机器人由起点到终点的一条安全、节能或行程最短的最优或次优通路[2]。为此，文献[3-5]提出了人工势场法、可视图法、人工神经网络等方法。然而，人工势场法容易产生极小值点，导致移动机器人按此路线行走时停滞不前，不易实现全局路径规划；可视图法产生的规划路径复杂且效率不高；神经网络初始训练条件不易产生。通常情况下，机器人的路径规划都可以转化为一个有约束的非线性优化模型问题；针对这方面，遗传算法(Genetic Algorithm, GA)汲取了仿生自寻优的全局收敛、编码操作和并行性计算等特点，在解决非线性问题上具有良好的适用性和鲁棒性，加之其自身结构的开放性且易与问题结合，近年来，已经被广泛应用于复杂环境下的路径规划。而传统的遗传算法本身易早熟陷入局部最优，算法运行效率较低，不能保证对路径规划的可靠性及其运行效率的要求。

为改善传统遗传算法(Traditional Genetic Algorithm, TGA)的这一缺陷，从而更好运用到路径规划中去，本文结合实际餐厅内部规律布局对其进行有针对性的改进和优化，用于餐厅服务机器人的路径规划。基于此，本文在前人研究的基础之上，针对TGA的不足和餐厅实际环境的特点，提出一种改进遗传算法——HLGA(Halton-Levenshtein Genetic Algorithm)的餐厅服务机器人路径规划方法。仿真结果表明该算法能在实际餐厅环境中快速找到存在的最优路径。

1 改进遗传算法

美国密执安大学J.Holland教授最早提出遗传算法，它是通过模拟自然界生物自然选择和进化而形成的一种全局优化概率搜索的自适应算法[6]。该算法需要的预设参数有种群规模、最大进化代数、交叉和变异概率等；一般包括选择、交叉、变异三个过程；通过不断的迭代，最终得到问题最优解。

1.1 初始种群

1.1.1 基于拟随机序列的种群初始化

遗传算法中，人工选择初始种群费时费力；随机选择初始种群难以满足路径有目的性和无障碍性的要求，且易于生成非通路路径个体，因此，本文利用拟随机Halton序列[7-8]具有较随机序列更高的均匀性、可以产生低差异度个体、获取更多目标信息、执行简单等特点来产生初始种群。

1.1.2 基于Levenshtein距离优化初始种群

初始种群产生后，种群个体之间存在一定相似度。若相似度过大则会减弱种群多样性，使算法易陷入局部最优造成遗传进化停滞；反之则会增强种群多样性，进而使算法运行时间过长，不利于实际问题的解决。本文采用编辑距离(又称Levenshtein距离[9])对初始种群进行个体的相似度优化。

编辑距离是由俄国科学家Levenshtein提出用来计算两字符串相互转化所需最少删除、替换和插入次数的一种算法。个体采用二进制编码，编码后的不同个体可看作不同字符串。初始种群矩阵为I，随机选择两个体Ii和Ij，相似度计算公式[10]如式(1)所示：

α=1-DIS/max(Leni,Lenj)

(1)

其中：α为两个体相似度，取值范围为[0,1]。两字符串间的编辑距离(Distance, DIS)，max表示取两字符串长度的较大者。

1.2 适应度函数

以安全性、路径平滑性和最短距离作为规划路径的可行性评价因子，从而得到个体适应度评价函数。

1.2.1 安全性评价因子

由已知的障碍物和栅格位置坐标信息,可确定路径点的位置距其周围障碍物边界距离的最小值di，由式(2)可得出安全性评价因子f1，如图1所示。

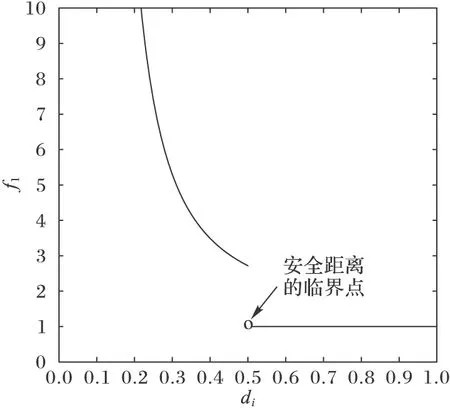
图1 安全性评价因子函数图像

(2)

其中，安全距离(Safety distance,Sd)为0.5(栅格边长的一半)，表示路径点与障碍物的距离。

由图1可知，当安全距离小于设定值时，安全性评价因子函数的值迅速增大。反映到HLGA中表现为：相应的个体适应度函数值增大，被下一代选中的概率迅速下降。

1.2.2 平滑性评价因子

机器人移动过程中，平滑路径更易于其运行且可减少能耗，加之服务机器人自身的物理特性，决定它在移动过程中不能以较大角度进行变向，因此需要加强所规划路径的平滑性——路径转向角尽可能小。如式(3)所示：

(3)

其中：a=(xi-xi-1,yi-yi-1)，b=(xi+1-xi,yi+1-yi)。

1.2.3 距离评价因子

机器人移动过程中，规划的路径长度评价函数——各路径点之间的欧氏距离总和，由式(4)确定：

(4)

为使参数易于调整，排除三项因子简单求积引起的不稳定因素，尽可能使函数简单；先对三项因子归一化处理，然后采用各因子乘积形式作为适应度函数，如式(5)所示：

fitness=f1×f2/(num×π)×f3/dsum

(5)

其中，路径的拐点总数(number,num)和由起点到终点与它们之间垂直交叉点的距离总和(distance sum,dsum)。

由式(5)可知，以fitness作为适应度函数，安全性越高，路径越平滑，路径长度越短时适应度函数值越小。

1.3 遗传算子与概率调整公式

1.3.1 选择算子

采用比例选择算子，个体赌轮盘选择方法向下一代进化。第i个个体被选择的概率P(Ii)由式(6)所示：

(6)

其中，fitness(Ii)表示第i个个体的适应度值。

1.3.2 交叉与变异算子

对交叉、变异概率的选择，谢鹏等[11]提出了能保证种群多样性的自适应选择机制遗传算法，但是这些方法都是依据个体适应度与当前代算术平均适应度(Arithmetic mean,fa)的相对大小进行判定。当种群中有较多适应度较小个体或是有较多适应度较大个体时，fa就会变得更低或更高，那些略大于或略小于平均适应度的个体，就变成了适应度较高或较低的个体；加之fa只能大致衡量当代进化适应度的相对状况，并不能准确衡量整个遗传进化过程中个体适应度的相对大小，因此将fa作为判断个体适应度相对大小的标准具有一定缺陷。基于刘建文等[12]提出的基于个体相似度改进的自适应遗传算法(Adaptive Genetic Algorithm based on Improved individual Similarity， ISAGA)，改进了交叉概率和变异概率的调整公式，如式(7)和(8)所示：

(7)

(8)

其中：Pc1/Pc2=0.9/0.6，Pm1/Pm2=0.5/0.1，fmax、fmin表示种群个体的最大、最小适应度，两交叉个体中较大适应度(Cross individual fitness,fc)，变异个体适应度(Mutate individual fitness,fm)。

如图2所示，几何均值(Geometric mean,fG)与fa的整体进化趋势基本相同，但是fG始终小于fa，这就使得将fG作为交叉概率和变异概率的依据时，更容易得到较小适应度值的个体，提高算法收敛速度。

依据fG判断个体适应度的相对高低，可以从整个进化过程中较为准确的优化每一代种群进化，使得适应度值相对较高的个体以较高概率进行交叉，适应度值相对较低的个体以较高概率进行变异。最终，使种群更具多样性，更好排除局部最优达到全局最优，进而提高算法效率。

图2 两种均值的比较

1.3.3 平滑算子[13]

为保证机器人在较平滑路径上移动，添加平滑算子。首先计算所规划路径的拐角值并得到其fa，然后将大于均值的拐点附近等距离插入两新路径节点，且删除原路径节点。

HLGA整体流程如图3所示。

图3 HLGA流程

2 模型建立

以某餐厅实际布局位置原型图11 m×11 m为例，如图4所示，采用HLGA，对机器人的行走路径进行全局搜索，寻找出一条路径相对较短、较平滑且安全性较高的最优路径。

假设机器人的工作空间可用二维平面图表示(比例尺为1∶100)。空间中障碍物的位置和大小根据实际餐厅布局有规律的排列(不考虑其高度问题)，在机器人运行过程中，障碍物结构、体积及其位置信息均固定不变且已知。基于此，机器人的工作空间模型依据实际餐厅规模按比例确定仿真栅格地图。

为使机器人在栅格中自由移动，设定栅格尺寸略大于机器人的最大直径且固定。工作空间中不含障碍物称为分别代表障碍空间(餐厅的桌椅、吧台和洗手间等)和自由空间，110号栅格代表餐厅服务机器人的起点(Start point， Sp)。

图4 餐厅实际布局(局部)

如图5所示，初始种群规模或遗传进化代数越大，算法收敛至全局最优解的速率越快；然而，当两者至少有一个过大时，收敛速度与其呈现负相关关系；当进化代数为40，50，60时，可以得出对应不同情况下的最优点分别为(32，35.89)、(20，35.95)和(18，36.91)。综合算法收敛速度和实际情况，HLGA的初始种群和最大遗传进化代数分别设定为20，50。以ISAGA的交叉和变异概率进行对应参数设定，进一步设计仿真实验验证。

图5 种群规模和进化代数关系

3 仿真结果及分析

基于某餐厅实际布局图建立的抽象栅格地图模型，本文采用Matlab[14]进行仿真实验。仿真过程以序号110为起点Sp，以序号21为终点(End point， Ep)。针对经过实际餐厅环境下抽象形成的静态障碍栅格地图，分别利用TGA、ISAGA和HLGA，在同一环境下对餐厅服务机器人移动路径进行由起点到终点的仿真规划。3种算法的仿真实验预设参数如表1所示。

依据表1所示的参数预设值，在Matlab上运行3种不同算法各100次后，选取效果较优的路径规划仿真图，如图6所示；得到的路径规划图的相关参数信息，如表2所示。

表1 仿真实验参数预设

表2 3种算法运行效果对比

比较图6中3种算法的路径规划仿真图可知：在同一环境中进行路径规划时，利用HLGA和ISAGA产生的路径较短，且拐点总数较TGA明显减少；与ISAGA相比，HLGA规划方法产生的路径更平滑、更具有安全性、拐点更少，因此，HLGA在规划形成的路径效果上优于ISAGA和TGA，得到的移动路径也更适合于特定环境下的餐厅服务机器人的运行。

从表2中比较可以得出：1)在规划路径的安全性上，只有HLGA表现为安全，原因在于该算法在适应度函数中增加了安全性评价因子。2)在规划路径的长度上，HLGA在加强自身规划路径平滑性基础之上，仅仅较ISAGA增加了0.17，由此所带来的微小增大，较之TGA和ISAGA在规划路径平滑性方面的劣势，完全可以忽略。3)在规划运行的时间上，HLGA较ISAGA减少1.79 s，较TGA减少6.92 s，明显提高了算法的运行速度，即缩短了路径规划的时间，原因在于该算法结合领域知识所设计的初始种群的产生以及对其优化方法都降低了不行解的数量，从而提高了种群进化速度，使算法更容易快速收敛至全局最优解。4)当忽略算法平滑性因子的影响时，利用HLGA和ISAGA产生的规划路径长度相等，均为16.24；而上述图6(c)图较之图6(b)在规划路径的拐点数上小1，原因在于HLGA采用的自适应交叉和变异概率调整公式将fG作为调整公式的标准，综合了每代种群与整个遗传进化过程的整体性。

基于HLGA，在不同起点Sp，不同终点Ep和任意自由栅格的起点Sp、终点Ep的条件下进行的路径规划均具有较优效果，如图7所示。经以上实验比较分析可知，本文提出的HLGA是可行有效的，无论在运行效率还是在路径规划的效果上均优于ISAGA和TGA。

图6 餐厅服务机器人路径规划——Matlab仿真结果

图7 基于HLGA的餐厅服务机器人路径规划

4 结语

本文针对TGA易产生早熟且运行速度慢的缺点，提出了HLGA。与TGA和ISAGA相比，HLGA在运行时间上分别缩短了6.92 s和1.79 s；增加安全性因子，使规划的路径更具有安全性；调整交叉和变异概率公式，使算法更好、更快地收敛至全局最优解；增加平滑算子，使规划路径更合理，可适当减小机器能耗。通过以实际餐厅布局为环境模型进行的仿真实验，确实提高了算法的效率和性能，使得本文提出的HLGA具有可行性，运用到餐厅服务机器人路径规划上是有效的。后续工作重点是，在有动态障碍物的环境中，餐厅服务机器人的路径规划及其算法研究。

References)

[1] SEUNGHWAN P, WONPIL Y, JAEIL C. A user reactivity research for improving performance of service robot[C]// Proceedings of the 8th International Conference on Ubiquitous Robots and Ambient Intelligence. Piscataway, NJ: IEEE, 2011: 753-755.

[2] 邓志燕,陈炽坤.基于改进遗传算法的移动机器人路径规划研究[J].机械设计与制造,2010,2(7):147-150.(DENG Z Y, CHEN C K. Path planning for moving robot based on improved genetic algorithm [J]. Mechanical Design and Manufacturing, 2010, 2(7): 147-150.)

[3] LI G H, TONG S G, CONG F Y. et al. Improved artificial potential field-based simultaneous forward search method for robot path planning in complex environment [C]// Proceedings of the 2015 IEEE/SICE International Symposium on System Integration. Piscataway, NJ: IEEE, 2015: 760-765.

[4] MA Y C, ZHENG G, PERRUQUETTI W. Cooperative path planning for mobile robots based on visibility graph [C]// Proceedings of the IEEE 32nd Chinese Control Conference. Piscataway, NJ: IEEE, 2013: 4915-4920.

[5] ZHANG H. A preliminary study on artificial neural network [C]// Proceedings of the 2011 International Conference on Information Technology and Artificial Intelligence Conference. Piscataway, NJ: IEEE, 2010: 336-338.

[6] 王小平,曹立明.遗传算法理论、应用与软件实现[M].西安:西安交通大学出版社,2002:2-5.(WANG X P, CAO L M. Genetic Algorithm Theory, Application and Software Implementation [M].Xi’an: Xi’an Jiaotong University Press, 2002: 2-5.)

[7] ATANASSOV E, KARAIVANOVA A, GUROV T. Quasi-random approach in the grid application SALUTE [C]// PPAM 2009: Proceedings of the 8th International Conference Parallel Processing and Applied Mathematics. Berlin: Springer, 2010: 204-213.

[8] SCHLIER C. On scrambled Halton sequences [J]. Applied Numeri-cal Mathematics, 2008, 58(10): 1467-1478.

[9] LEVENSHTEIN V. Binary codes capable of correcting deletions, insertions and reversals [J]. Soviet Physics Doklady, 1996, 10(8): 707-710.

[10] 牛永洁,张成.多种字符串相似度算法的比较[J].计算机与数字工程,2012,40(3):14-16.(NIU Y J, ZHANG C. Comparison of multi-string similarity algorithms [J]. Computer and Digital Engineering, 2012, 40(3): 14-16.)

[11] 谢鹏,张红梅.基于自适应遗传算法的EHA控制器优化设计[J].传感技术学报,2016,29(6):909-914.(XIE P, ZHANG H M. Optimum design of electro-hydrostatic actuator controller based on adaptive genetic algorithm [J]. Chinese Journal of Sensors and Actuators, 2016, 29(6): 909-914.)

[12] 刘建文,丁洁玉,潘坤,等.基于个体相似度的改进自适应遗传算法研究[J].青岛大学学报(工程技术版),2016,31(1):16-19.(LIU J W, DING J Y, PAN K, et al. Improved adaptive genetic algorithm based on individual similarity [J]. Journal of Qingdao University (Engineering & Technology Edition), 2016, 31(1): 16-19.)

[13] 束磊.基于栅格地图的月球车任务层路径规划及平滑处理[D].哈尔滨:哈尔滨工业大学,2013:50-59.(SHU L. Mission-level path planning and smoothing of lunar rover based on grid map [D]. Harbin: Harbin Institute of Technology, 2013: 50-59.)

[14] 雷英杰,张善文.Matlab遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2014:62-94.(LEI Y J, ZHANG S W. Genetic Algorithm Toolbox and Application about Matlab [M]. Xi’an: Xidian University Press, 2014: 62-94.)

This work is partially supported by the National Public Welfare Industry Research Projects (201410028- 02).

XULin, born in 1990, M. S. candidate. His research interests include service robot, intelligent control, path planning.

FANXinwei, born in 1973, Ph. D., senior engineer. His research interests include robot, pattern recognition and intelligent control, data mining.

Pathplanningforrestaurantservicerobotbasedonimprovedgeneticalgorithm

XU Lin*, FAN Xinwei

(CollegeofQualityandSafetyEngineering,ChinaJiliangUniversity,HangzhouZhejiang310018,China)

Since the Genetic Algorithm (GA) is easy to produce premature phenomenon and has slow convergence rate, an improved GA based on Traditional GA (TGA), called HLGA (Halton-Levenshtein Genetic Algorithm), was proposed for path planning of real restaurant service robots. Firstly, the similarity method based on edit distance optimized the initial population of quasi-random sequence; secondly, the improved crossover probability and mutation probability adjustment formula based on the adaptive algorithm were adopted to cross and mutate the individuals after they had been selected. Finally, the individual fitness values of the safety evaluation factor functions were calculated, and the global optimal solution was obtained by comparison and iteration. Through theoretical analysis and Matlab simulation, the running time of HLGA was decreased by 6.92 seconds and 1.79 seconds compared with TGA and Adaptive Genetic Algorithm based on Improved independent Similarity (ISAGA), and the actual path of planning was more secure and smooth. The simulation results show that HLGA can effectively improve the quality of path planning in practical applications, meanwhile reduces the searching space and the planning time.

Genetic Algorithm (GA); restaurant service robot; quasi-random sequence; edit distance; path planning

TP249; TP18

:A

2017- 01- 09;

:2017- 03- 01。

国家公益性行业科研项目(201410028- 02)。

徐林(1990—)，男，安徽阜阳人，硕士研究生，主要研究方向：服务机器人、智能控制、路径规划； 范昕炜(1973—)，男，江西广丰人，高级工程师，博士，主要研究方向：机器人、模式识别与智能控制、数据挖掘。

1001- 9081(2017)07- 1967- 05

10.11772/j.issn.1001- 9081.2017.07.1967