含临界参数和临界指数的双调和方程多重解

刘 春 晗

(齐鲁师范学院数学学院，山东 济南 250013)

含临界参数和临界指数的双调和方程多重解

刘 春 晗

(齐鲁师范学院数学学院，山东 济南 250013)

利用对称形式的山路引理，讨论了一类含临界参数和临界指数的奇异双调和方程，获得了方程的无穷多个非平凡解.

双调和方程；对称形式的山路引理；临界指数；非平凡解

1 预备知识

1983年，Brezis-Nirenberg给出了求解含临界指数方程的方法，吸引了国内外众多学者对含临界指数的非线性方程进行研究.文献[1]研究了双调和方程

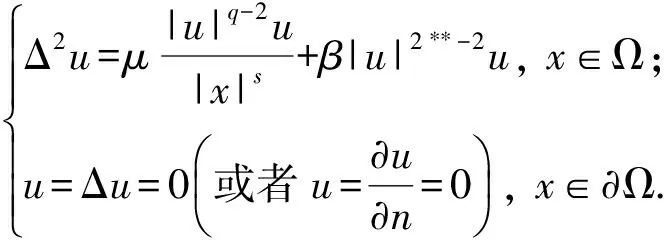
文献[2]讨论了方程

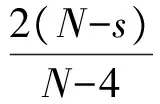
本文利用对称形式的山路引理，研究了奇异双调和方程

(1)

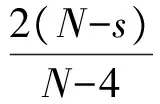
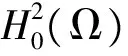
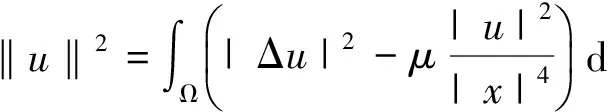
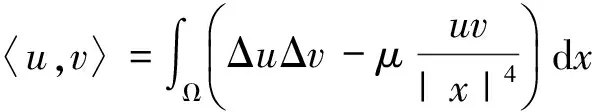
首先在空间H中讨论以下特征值问题非平凡解的存在性：

(2)

第一特征值定义为

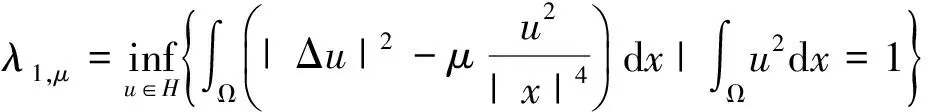
第二特征值定义为

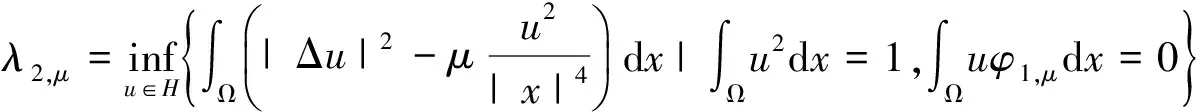
类似地，可以定义第n个特征值为

其相应的特征函数记作φn，μ.

问题(1)的弱解就是泛函

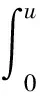
对于任意的φ∈H，

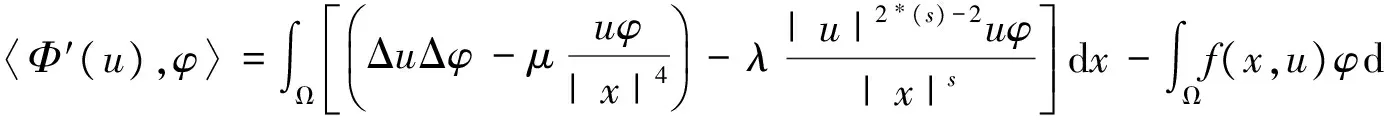
下面给出一些假设条件：

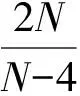
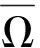
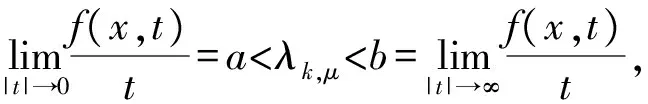
(Ⅴ)f(x，-t)=-f(x，t).

定义1[3]设Φ∈C1(E，R)，称Φ关于每一个c∈R满足(PS)c条件，如果n→∞时，满足

Φ(un)→c，Φ′(un)→0

的任意数列un均有收敛子列；称Φ满足(PS)条件，如果Φ关于任意c∈R满足(PS)c条件.

定义2[3]设Φ∈C1(E，R)，称Φ关于每个c∈R满足(C)c条件，若当n→∞时，任意满足

Φ(un)→c，(1+‖un‖)Φ′(un)→0

的数列un都有收敛子列；称Φ满足(C)条件，如果Φ对于任意c∈R满足(C)c条件.

引理1[2](Sobolev-Hardy不等式) 设0≤s≤4，2≤q≤2*(s).则存在常数c1>0使得

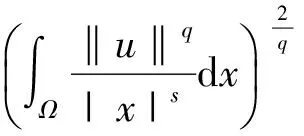
并且空间H嵌入到Lq(Ω)是紧的.

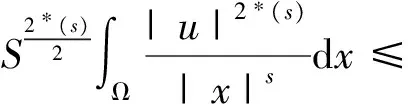
(3)

类似于文献[4]中引理3—4，可证下面两个引理成立.

引理2 特征值问题(2)有一个非平凡解φ1，μ.

引理3 当n→∞时，λn，μ→+∞.

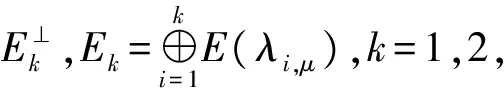
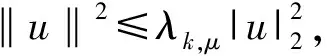
引理5[3](对称形式的山路引理) 假设Φ∈C1(E，R)，Φ(θ)=0.则：

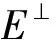
如果Φ满足(PS)条件，则Φ有无限多个对应正临界值的临界点.

注1 若Φ满足(C)条件，则引理5的结论也成立.

2 主要结果

定理1 如果f(x，t)满足假设(Ⅰ)—(Ⅴ)，则存在λ*>0，当0<λ<λ*时，方程(1)存在无穷多个非平凡解.

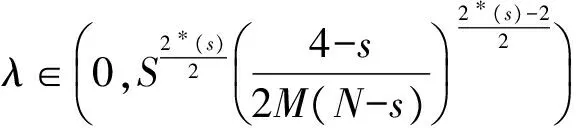
(1+‖un‖)Φ′(un)→0，Φ(un)→c，

(4)

则un是有界的.若不然，设‖un‖→+∞，由假设(Ⅳ)可知存在r>1使得

f(x，t)t-2*(s)F(x，t)≥-δ|t|σ，∀|t|>r.

(5)

设Ωn={x∈Ω||u|>r}，由(4)与(5)式，存在M0>0使得

2*(s)(1+c)≥2*(s)Φ(un)-〈Φ′(un)，un〉=

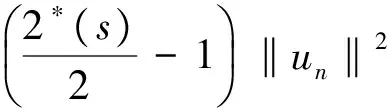
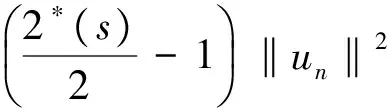
矛盾.因此un在H有界，于是un在H中有弱收敛子列，仍记为un，弱收敛极限记为u.当n→∞时，

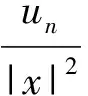
由Brezis-Lieb引理、Vitali定理及文献[6]可知

(6)

(7)

(8)

从而

Φ(un)-Φ(u)-Φ(un-u)=o(1)，

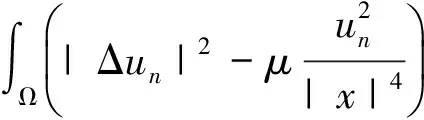
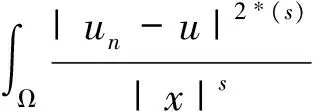
由(4)式及Φ′(u)=0有

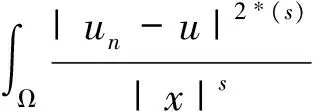
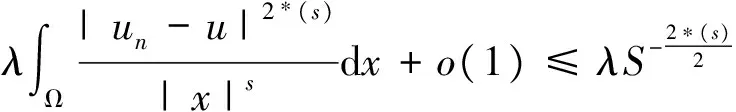
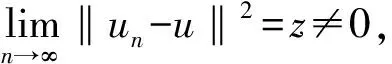
M+o(1)≥Φun=Φu+Φun-u+o(1)≥

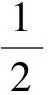
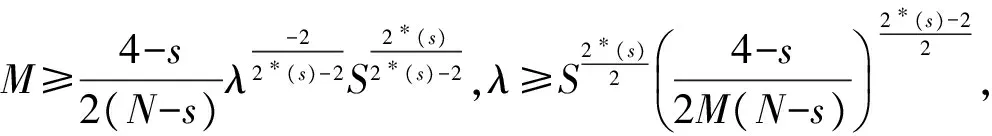
(ⅱ) 证明Φu满足引理5的其他条件.由假设(Ⅲ)，对任意ε>0，存在C2>0使得

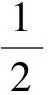
取ε=ε1充分小，使得λk，μ+ε1<λk+1，μ，利用(3)式、引理4和Sobolev-Hardy不等式，有

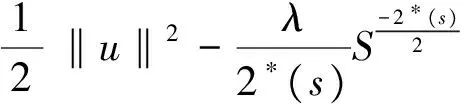
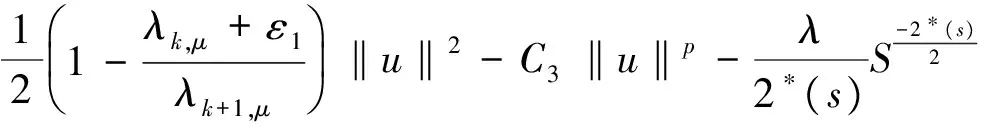
因为0≤s<4，故

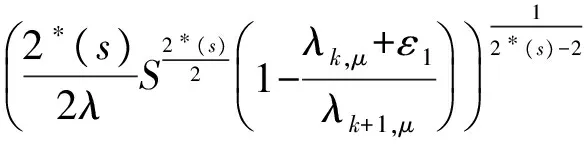
其中Bρ(θ)={u∈H|‖u‖≤ρ}.

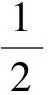
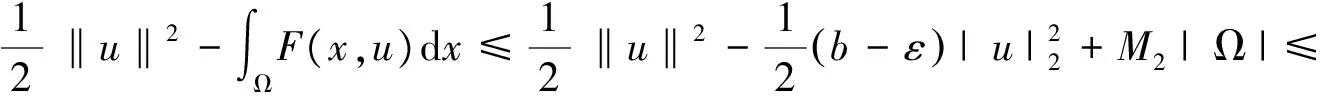
所以存在Rk>ρ，使得Φ(u)≤0，∀u∈EkBRk(θ)，k=1，2，….

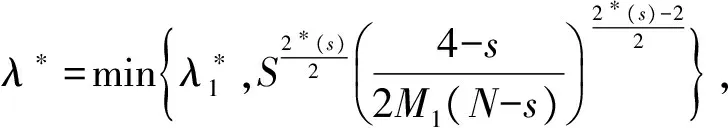
注2 存在R>0，使得2*(s)F(x，u)≤f(x，u)u，∀|u|>R，x∈Ω.从而∀|u|>R，x∈Ω有

f(x，u)u-2*(s)F(x，u)≥0>-δ|u|σ.

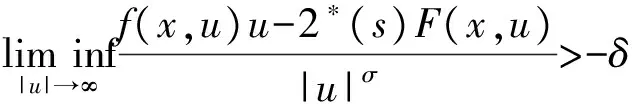
于x∈Ω一致成立.

因此假设(Ⅳ)比Ambrosetti-Rabinowitz型增长条件更弱.

注3 如果f(x，u)u-2*(s)F(x，u)→+∞，当|u|→∞时于x∈Ω一致成立，则

于x∈Ω一致成立.

[1] 王友军，沈尧天.一类含临界指数双调和方程变号解的存在性[J].应用数学，2009，22(2)：233-238.

[2] 杜刚，魏静.一类双调和方程变号解的存在性[J].数学的实践与认识，2011，41 (23)：172-177.

[3] CHANG K C.Infinite dimensional Morse theory and multiple solutions problems [M].Boston：Birkhäuser，1993：103-143.

[4] WANG Y J，SHEN Y T.Multiplicity of solutions for nonlinear biharmonic equation involving critical parameter and critical exponent[J].Chin Quart J of Math，2011，26(3)：317-324.

[5] MARINO B，ENRICO S.Semi-linear elliptic equations for beginners [M].London：Springer-Verlag，2011：39-54.

[6] SCHECHTER M，ZOU W M.Infinitely many solutions to perturbed elliptic equations [J].J Funct Anal，2005，228：1-38.

(责任编辑：李亚军)

Multiplicityofnontrivialsolutionsforbiharmonicequationinvolvingcriticalparameterandcriticalexponent

LIU Chun-han

(School of Mathematics，Qilu Normal University，Jinan 250013，China)

By a symmetric mountain pass lemma，a class of singular biharmonic equation involving critical parameter and critical exponent is discussed，and infinitely many solutions of the equations are obtained.

biharmonic equation；symmetric mountain pass lemma；critical exponent；nontrivial solution

1000-1832(2017)03-0008-05

10.16163/j.cnki.22-1123/n.2017.03.003

2016-03-02

国家自然科学基金资助项目(10971179)；山东省自然科学基金资助项目(ZR2016AB04)；齐鲁师范学院青年教师科研基金资助项目(2016L0603，2014L1001).

刘春晗(1981—)，男，硕士，副教授，主要从事非线性泛函分析及其应用研究.

O 175.25 [学科代码] 110·47

A