曲面插值细分规则的构造与应用

姜涛

（辽东学院师范学院，辽宁丹东118001）

【基础科学理论与应用】

曲面插值细分规则的构造与应用

姜涛

（辽东学院师范学院，辽宁丹东118001）

为解决飞行模拟器及一些三维全息投影模拟器中对三维地形地貌的模拟要求，文中构建了一种曲面插值细分规则，并将该细分规则应用于地形地貌的仿真。通过调整插值多项式的参数生成理想的地形形状。实验表明，该方法为简单、快速模拟自然地形地貌仿真提供了一种有效手段。

细分法；细分规则；插值细分法；地形地貌模拟

地形地貌的模拟是计算机图形学的一项重要内容，它对地理信息的采集模拟有着重要意义。同时，在飞行器的仿真等虚拟实现、三维游戏的地形虚拟实现、3D全息投影中也有着重要应用。

在地形地貌模拟问题的传统解决过程中，通常是先采集数据点，然后应用数据点构造多项式函数，最后对函数求新的插值点及对应值，再通过计算机模拟出来。当显示结果不理想时，需要重新构造函数或重新求插值点及对应值，也就是曲面造型上的离散——连续——离散的传统模式［1］。显然，这种构造图形的方法不符合计算机对图形模拟显示的特点，也过于繁琐和复杂，这对于有些复杂问题的解决是不利的，有时是无法实现的。为符合计算机对图形模拟显示的特征——离散性特征，显然，在图形显示过程中，不通过构造空间曲面函数，再求曲面上的点，而是在图形显示过程中，直接应用已有的控制顶点生成离散点，再在图形显示时只通过离散点显示的细分法更符合这种图形模拟显示特征。

细分法（subdivision）是一种离散化的曲面的造型方法，它的构造思想是：从一个特征网格开始，先按照适当选取的细分规则，在给定初始特征网格中插入新顶点，再连接这些新顶点得到新特征网格，所得新特征网格是初始特征网格的加细［2-3］。不断重复上述过程，随着细分的不断进行，特征网格就被逐渐细化，其极限状态就是一张曲面，称为递归细分曲面。细分方法用不断细分的多边形网格在允许的误差范围内来代替曲面［4］。

现在提出的细分规则很多，也有针对细节处理的。文中提出的细分规则，是针对一般的曲面模拟情况提出的细分规则。文献［5］是从总体上对两种细分思路所得到的细分曲线、曲面的特征区别讨论，解决了两大类细分方法在使用时的选择依据。依据文献［5］对插值细分法与割角细分法的特点比较可知，地形地貌的模拟问题中，主要对整体形状的控制。因此，插值细分法所得细分曲面在曲面造型中符合地形地貌模拟的特征要求。

Dyn的四点插值细分法是1987年Dyn和Levin在提出的四点插值法。Dyn和Levin在提出的四点插值法在插值细分法中是一个经典的插值细分法，是采用边分裂的方法加入新顶点的插值方法。本文首先，构造一个比较简单的面点细分规则，再应用Dyn四点插值细分法对曲面的边点进行细分。这样构建的细分规则算法简单，并且具有良好的收敛性。并采用在本文中提出的插值细分规则对地形地貌进行模拟。通过matlab软件对其模拟效果进行仿真实验，实验证明该方法是一种简单、快速、有效且便于控制的地形地貌模拟方法。

1 插值细分规则

1.1 面点细分规则

对于面点的细分采用四边形网格细分，即由不在同一等高线上的相邻四点构成四边形网格。在此四边形基础上，将风格细分，每次细分都生成新的四边形网格。在细分过程中使四边形面积逐渐减小。

其细分规则如下：

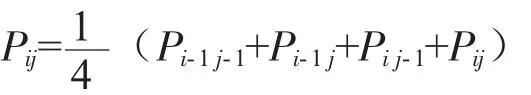
1.2 边点细分规则

对于边点的细分采用Dyn的四点插值细分法，该插值细分法将保留原有的顶点，在保留上层细分旧点的同时插入新点。Dyn的四点插值法是采用边分裂的方法加入新顶点的插值方法。

其细分迭代规则如下：

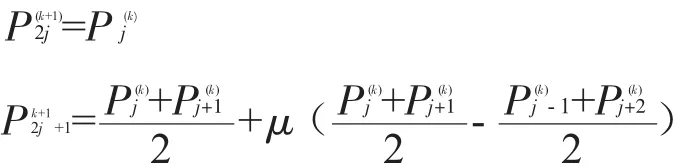
其中j=0，1，…，2kn-2，μ为参数，且时会具有很好的光滑性［4］。

2 细分规则的几何解释

2.1 面点细分规则的几何解释

面点的细分可用图1所示的几何关系进行解释。

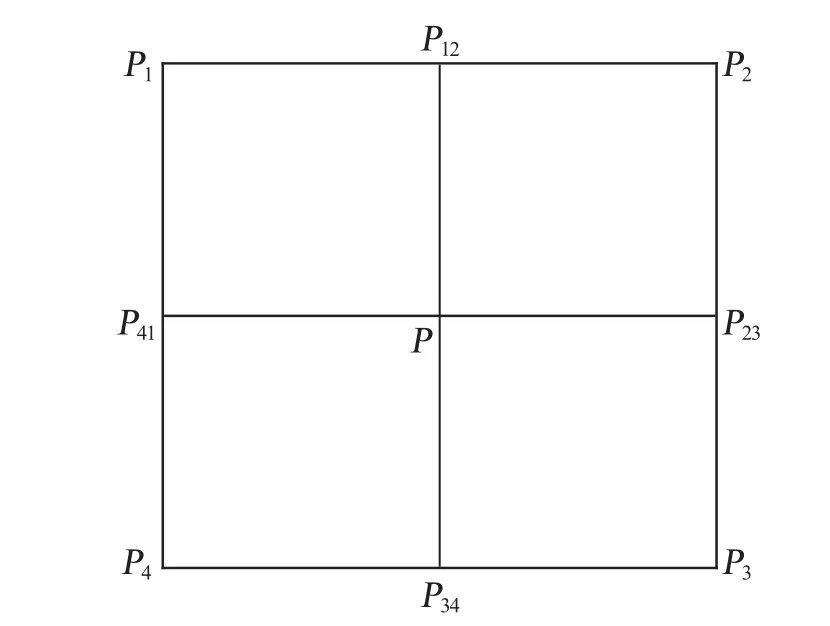
图1 面点细分规则的几何解释

由图1所示，在面点的分裂过程中，采用对特征多面体的原有四个相邻控制顶点进行均分方式生成新控制顶点，进而通过插值生成新控制顶点。

显然，P12，P23，P34，P41，满足下面等式关系：

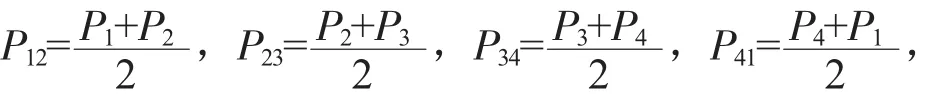
进而可得

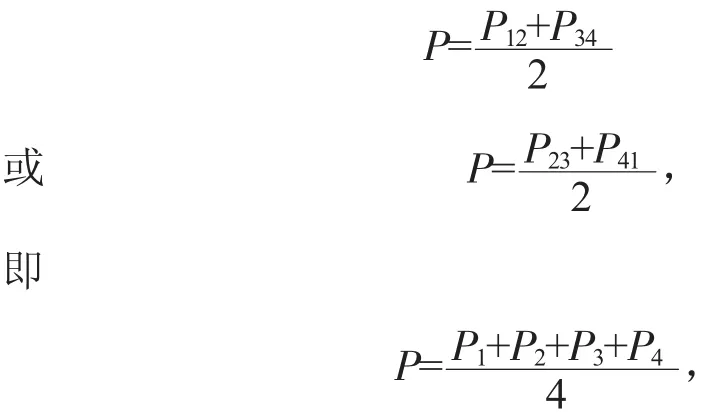
2.2 边点细分规则的几何解释

Dyn的四点插值细分法可用如图2所示的几何关系进行解释。

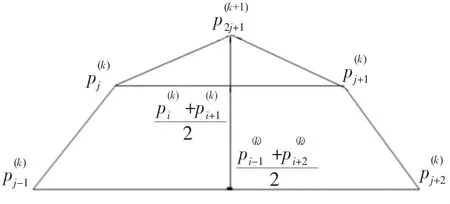
图2 Dyn四点细分规则的几何解释

由图2所示，Dyn的四点插值细分法是在边上分裂、堆彻的方式进行插值，使边上相邻点间的距离变小，进而使得曲线变得相对光滑。Dyn的四点插值细分法的从往的应用中多用于曲线的细分中，而在此则应用在边点的细分建立上。

3 细分规则的细分效果讨论

2.1 面点细分规则的细分效果讨论

取空间曲面的控制顶点｛P1，P2，P3，…，P19｝，由这些控制顶点生成初始特征空间曲面，及应用本细分规则经一次细分所得细分曲面分别如图3、图4所示。

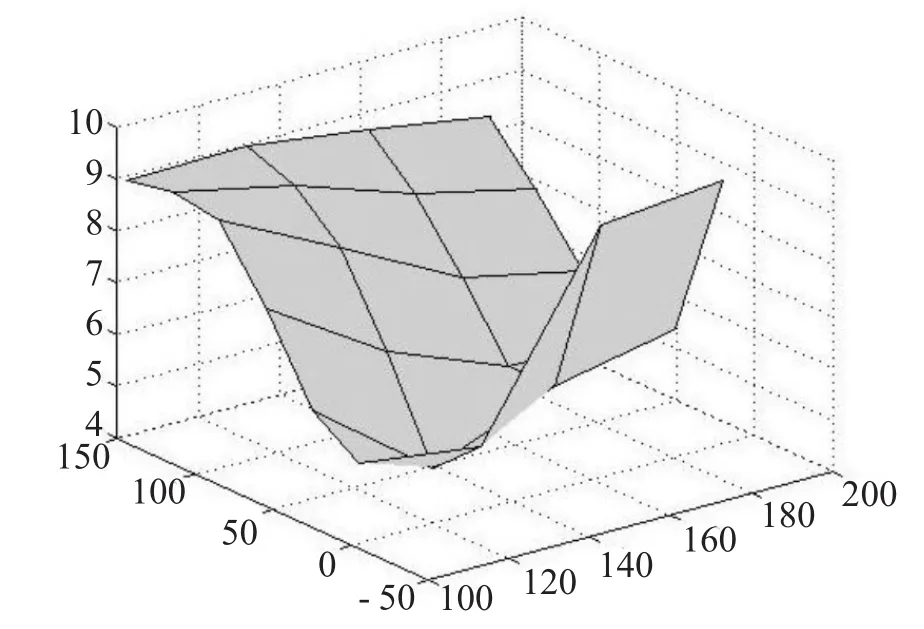
图3 初始特征空间曲面

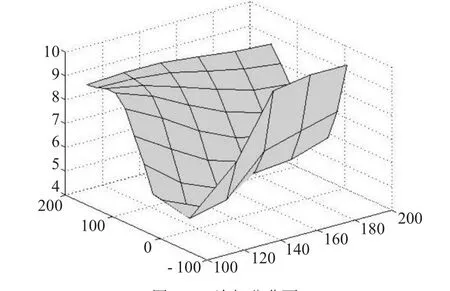
图4一次细分曲面

图5 、图6分别为经二次、三次细分所得细分曲面。

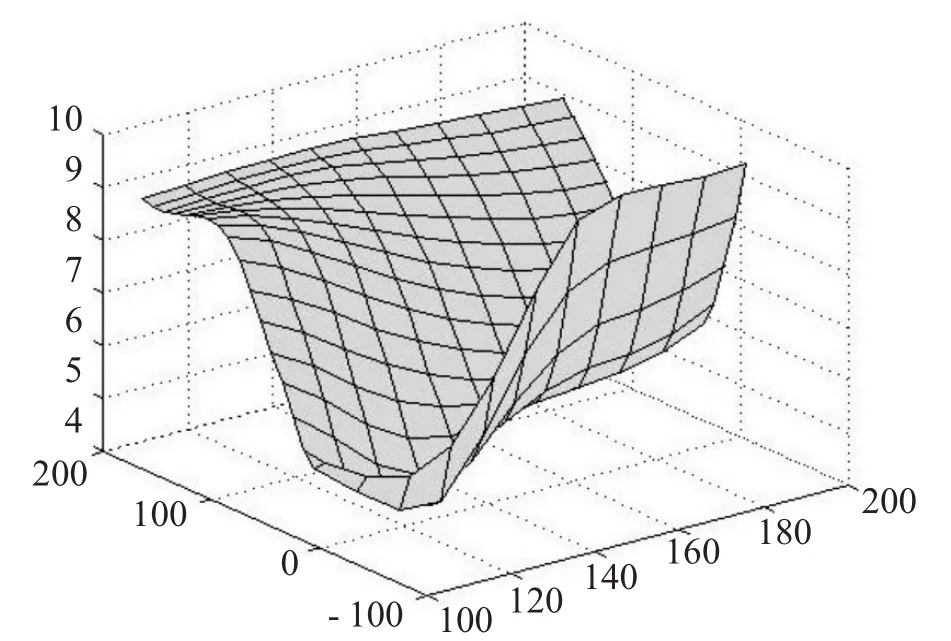
图5 二次细分曲面

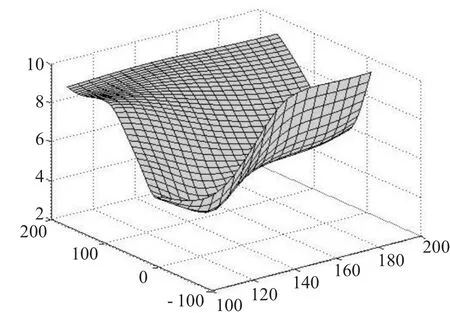
图6 三次细分曲面

由图2至图6可见该细分方法所得的细分曲面具有很好的光滑性，而且细分曲面的收敛速度是比较快的，换句话说，该细分方法具有很好的细分效果。

2.2 边点细分规则的细分效果讨论

特征多面体的边点可构成空间曲线，下面以空间特征多边形为例应用该细分规则分别演示特征多边形开放与特征多边形封闭两种情形所得的细分曲线效果。

(1)特征多边形为开放多边形情形

取特征多边形的控制顶点集｛P1，P2，P3，P4｝,由这些这控制顶点所得的开放形控制多边形，如图7所示。对此控制多边形应用边点细分规则取μ=进行一次细分得新的控制多边形，如图8所示。

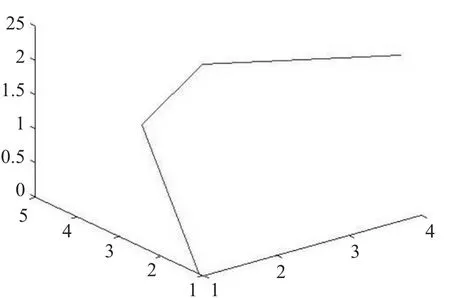
图7 开放的初始控制多边形

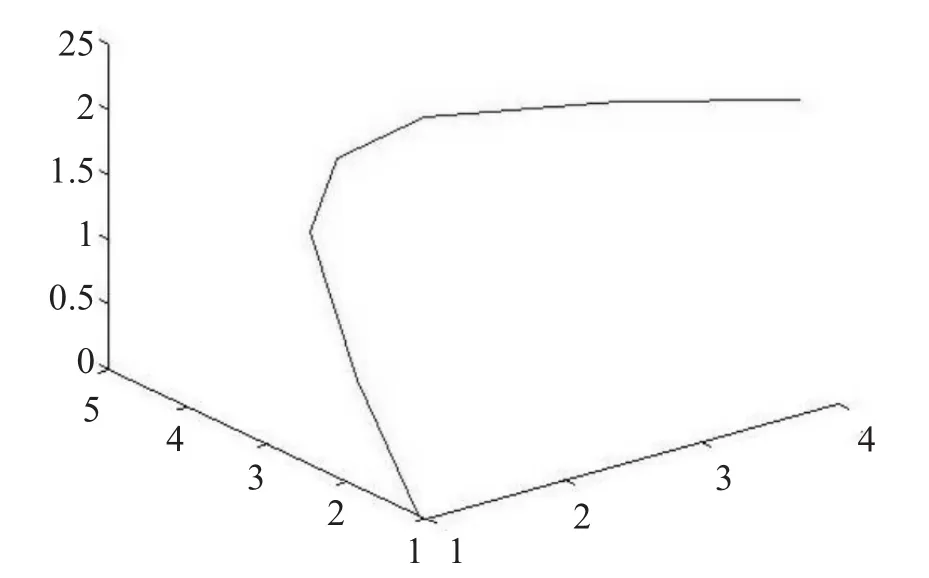
图8 开放的一次细分曲线

经四次细分后将得到较光滑的细分曲线，如图9所示。其最终细分曲线与初始控制多边形比较效果，如图10所示。

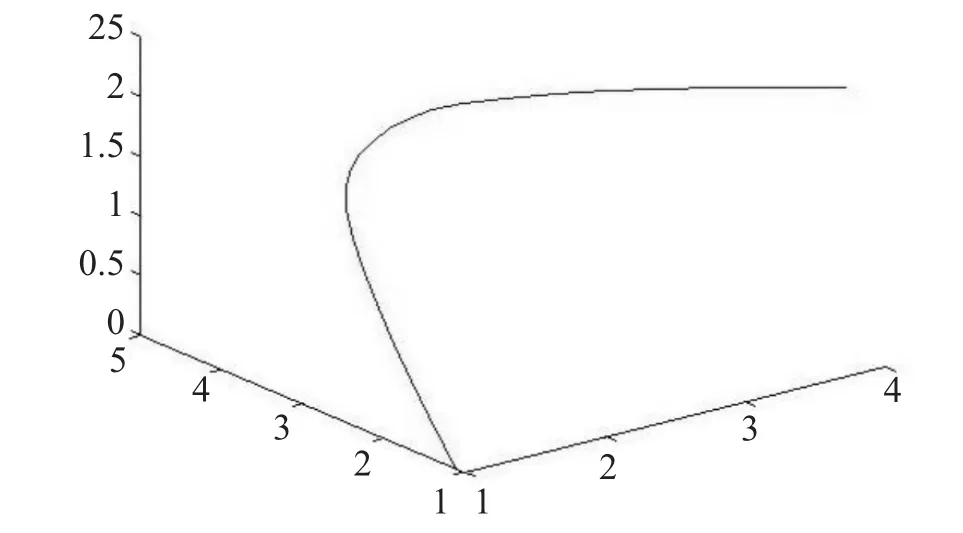
图9 开放的四次细分曲线

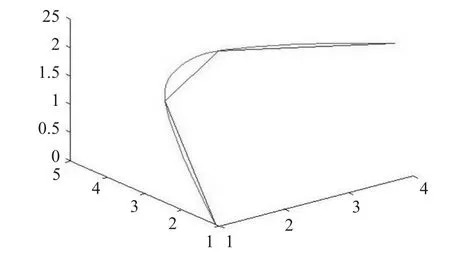
图10 开放的最终细分曲线与初始控制多边形比较

从图10的比较可见，边点的细分效果较好。

(2)特征多边形为封闭多边形情形

仍取特征多边形的控制顶点集｛P1，P2，P3，P｝4,由这些这控制顶点所得的封闭形控制多边形，如图11所示。对此控制多边形应用边点细分规则取进行一次细分得新的控制多边形，如图12所示。

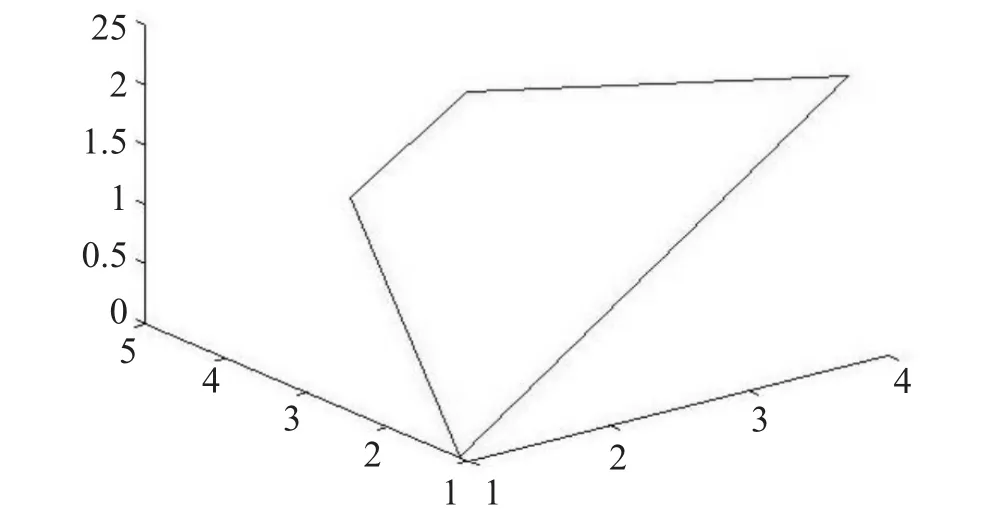
图11 封闭的初始控制多边形

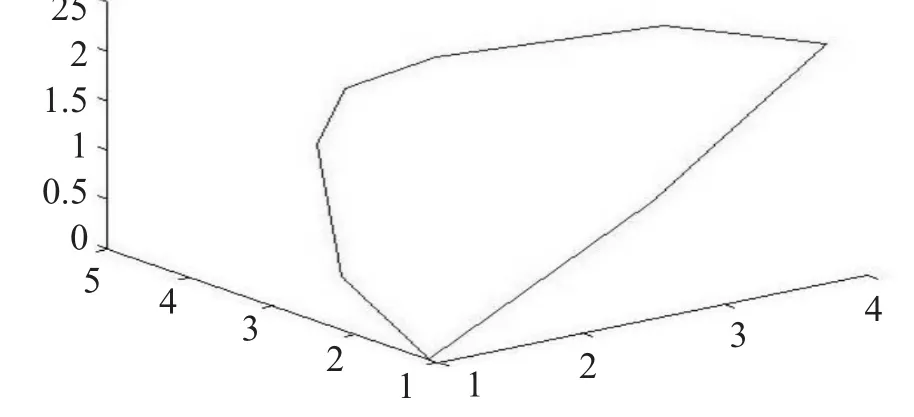
图12 封闭的一次细分曲线

经四次细分后将得到较光滑的细分曲线，如图13所示。其最终细分曲线与初始控制多边形比较效果，如图14所示。

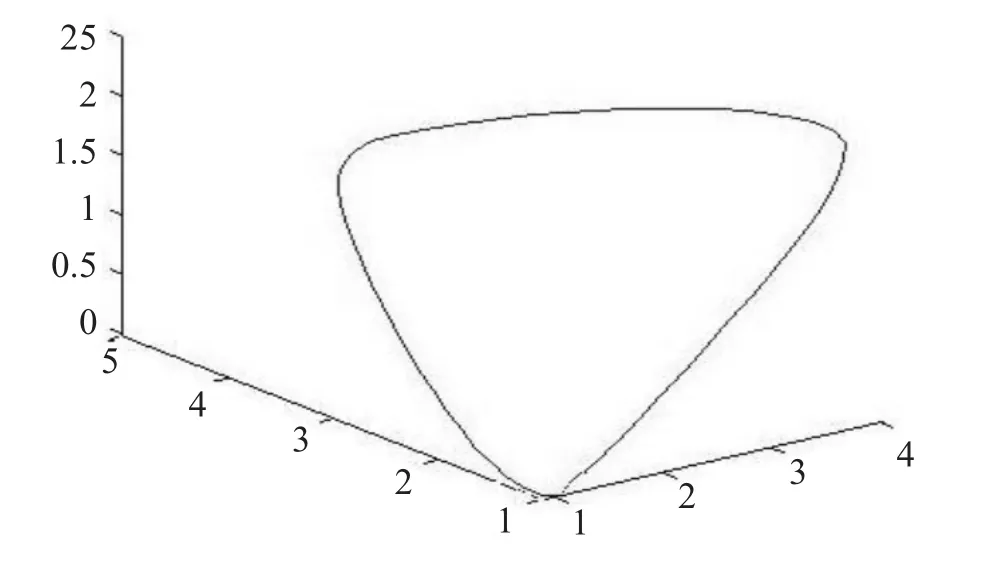
图13 封闭的四次细分曲线

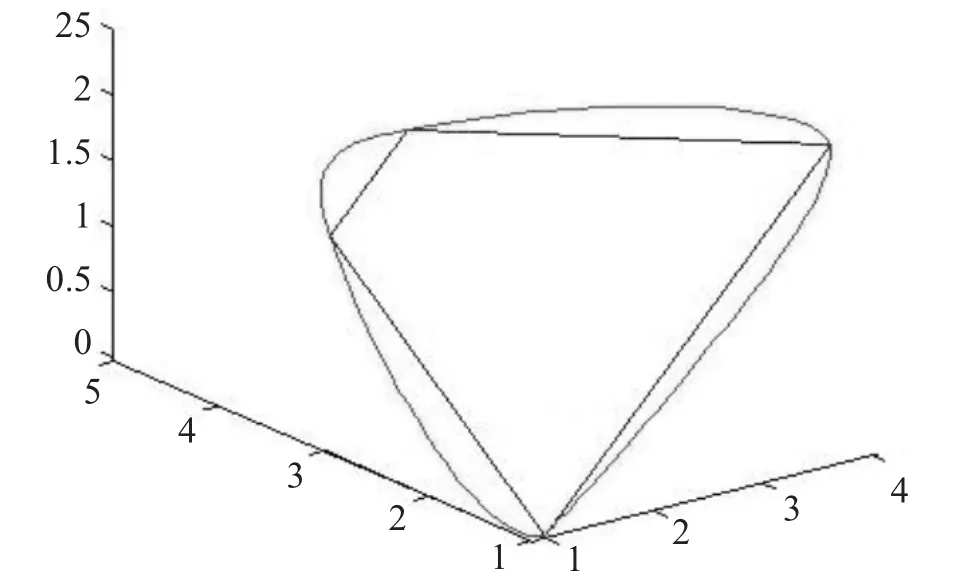
图14 封闭的最终细分曲线与初始控制多边形比较

由此可见，Dyn的四点插值细分法应用在边点的细分过程中，所得的边点细分效果还是比较好。综上所述，该细分过程无论是边点的细分，还是面点的细分，整个细分过程中都具有较好的收敛效果和较快的收敛速度。

4 细分规则在地形地貌模拟中的应用

采集105个控制顶点，如表1。

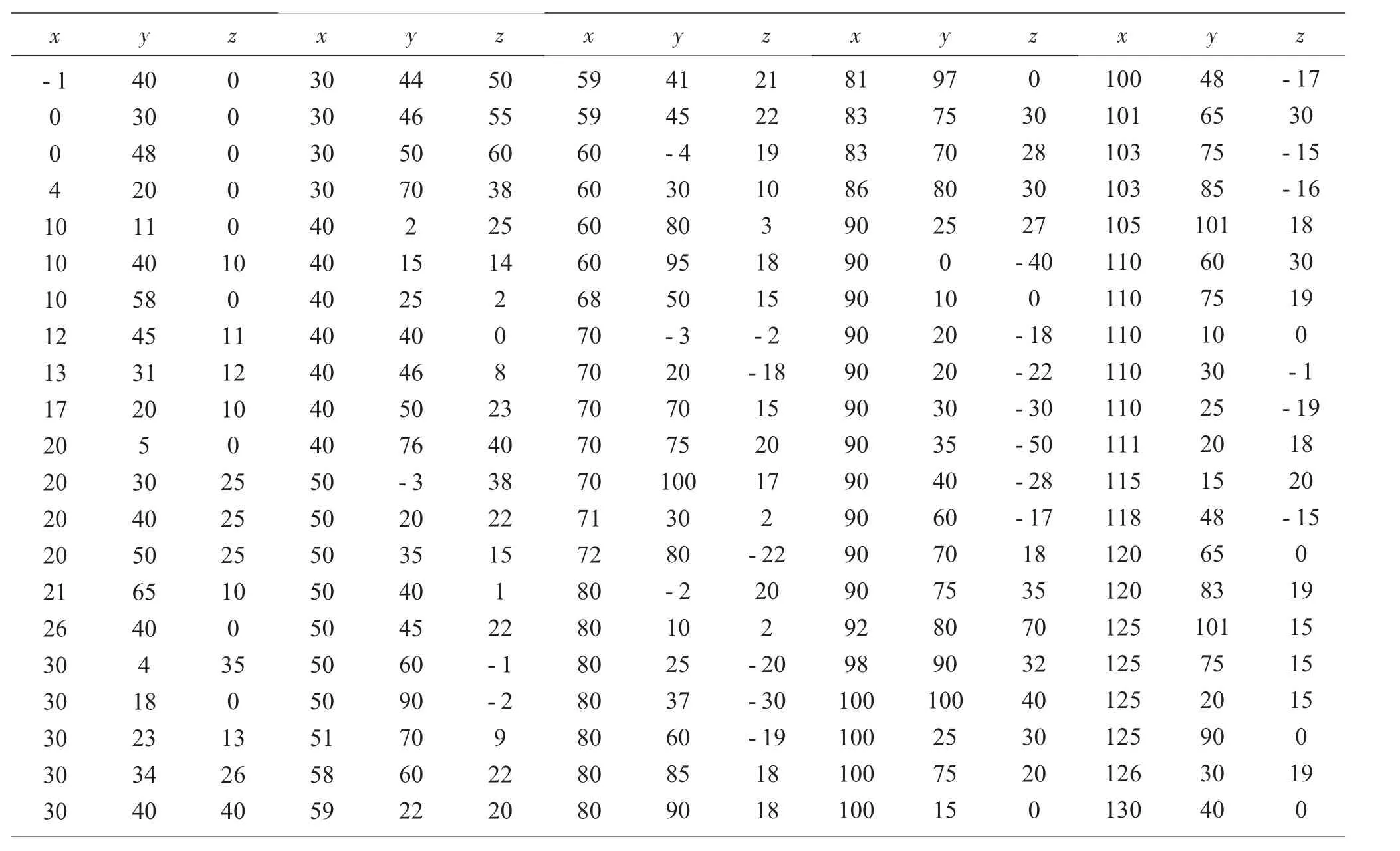
表1 控制多边形控制顶点

生成控制顶点集V=｛P1，P2，…，P105｝，借助matlab软件模拟地形的特征曲面，如图15所示。

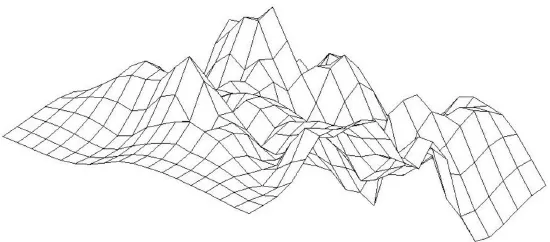
图15 地形的初始特征曲面

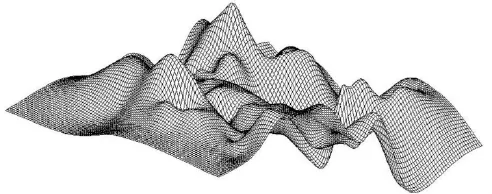
图16 地形的四次细分曲面

应用matlab软件对此地形进行渲染，模拟成山林地地貌，如图17所示

图17 地形模拟山林地效果图

5 结论

随着计算机辅助图形设计的广泛应用，地形地貌的模拟越来越多的被人们关注与应用，应用本文构建的细分规则可以简单、快速、有效的模拟出相应的地形地貌。

同时，应用本文构建的细分规则也可以应用在其他3 D图形的模拟中，只要恰当的调整参数和改变细分次数，都可以得到满意的模拟效果。

［1］MICCHELLI C A，PRAULZSCH H.Uniform Refinement of

Curves［J］.LinearAlgebra&Application，1989（114/115）：841-870.

［2］骆岩林，汪国昭.生成曲线的有理稳定细分方法［J］.高校应用数学学报，1998，13（A）：61-66.

［3］骆岩林，汪国昭.几何造型的有理矩阵细分方法［J］.应用数学学报，1999，22（2）：161-168.

［4］张新芬.曲线设计的非线性细分法［D］.杭州：浙江大学数学科学学院硕士学位论文，2005.

［5］姜涛.插值细分法与割角细分法在几何构图中的比较分析［J］.辽东学院学报（自然科学版），2016，23

（1），72-76.

（责任编辑：龙海波）

Construction and application of a curved surface interpolation subdivision rule

JIANG Tao
（Teacher’s School，Eastern Liaoning University，Dandong 118003，China）

To meet the demand for simulating the 3D landform of flight simulator and other 3D holographic projection simulators，a curved surface interpolation subdivision rule was constructed and applied.The ideal terrain could be generated by adjusting the parameters of the interpolation polynomial.The rule is proved to be an easy，ast and effective way of landform simulation.

subdivision；subdivision rule；interpolation subdivision；landform simulation

O241；TP391

A

1673-4939（2017）03-0224-06

10.14168/j.issn.1673-4939.2017.03.14

2016-11-23

姜涛（1976—），男，辽宁鞍山人，硕士，讲师，研究方向：数学应用与数学教学。