利用有序互信息匹配包含非透明列的数据模式*

郭乐乐，林友芳，韩 升

北京交通大学 计算机与信息技术学院 交通数据分析与挖掘北京市重点实验室，北京 100044

利用有序互信息匹配包含非透明列的数据模式*

郭乐乐+，林友芳，韩 升

北京交通大学 计算机与信息技术学院 交通数据分析与挖掘北京市重点实验室，北京 100044

数据模式匹配是异构数据源数据合并过程中的核心环节，属于数据集成中的关键问题。目前已有许多数据模式匹配方法，但其中很大一部分方法由于过多依赖数据模式描述信息，导致通用性不足，很难应用于其他场景中。为此，提出了一种利用有序互信息的匹配包含非透明列名和列数据值的数据模式。该方法不依赖诸如列名、列类型、主外键依赖等数据模式描述信息，因此具有很强的通用性。在多个数据集上实验结果表明，该方法能够在大幅降低匹配花费时间的同时提高匹配结果的准确率。

数据模式匹配；非透明条件；互信息；无向图匹配

1 引言

从最基本的层面讲，数据模式匹配就是寻找从一个信息库的元素到另一个信息库的元素上的映射问题。对于关系型数据库来说，这里信息库中的元素指的就是属性列。模式匹配问题经常出现在企业兼并重组带来的数据库合并过程或多数据源数据集成过程中，而且随着数据规模不断扩大，该问题也变得日益突出。显然使用人工方法解决模式匹配问题会给数据管理人员带来沉重的工作负担，因此迫切需要解决该问题的自动化方法。经过十多年研究，许多研究者发现数据模式匹配问题会随着约束的不同而带来复杂程度方面的巨大差异，很难找到一种适用于所有领域数据的匹配方法。目前已经提出了许多数据模式匹配方法，根据研究方法的不同可以概括为以下几大类：

（1）基于模式描述信息的匹配方法。之前已经提出了很多基于模式描述信息的方法[1]，如根据列名[2]、列名同义词[3]，或者其他语言学[4]的列名相似性描述方法，但基于列名相似的方法都无法解决“同名异义”和“同义异名”的问题。此外，也有基于字段类型或主外键等信息的模式匹配方法。这些方法大多出现在早期研究中，由于使用或部分使用模式信息，导致这类方法通用性不足。

（2）基于机器学习的模式匹配方法。早年有Li和Clifton提出的基于BP（back propagation）神经网络的原型系统SemInt[5],也有Berlin和Motro提出的利用特征选择减少了参加匹配的模式中的属性列数目的方法[6]。近些年随着新的机器学习理论的不断涌现，有不少研究者受这些理论的启发提出了一些新的模式匹配方法。其中，将多种学习器结合到一起就是一种重要的思路[7-8]。比如Do和Rahm提出的COMA（combining match）系统通过分析属性列最大、最小值提供候选匹配结点，集成多种学习器进行匹配[9]。Algergawy等人使用聚类方法改进了COMA算法，也取得了不错的效果[10]。Rodrigues等人提出了基于主动学习的方法减少了需要领域专家提供的训练样本数量[11]。Ferragut和Laska提出了离散取值模型、字符位置模型以及原子型字符位置模式，结合非参贝叶斯方法计算模式中列之间相似度[12]，为模式匹配研究提供了新的思路。这类方法要么直接选取模式描述信息作为特征，利用样本训练学习器，要么学习器集合中包含基于模式描述信息的学习器，有的方法甚至需要领域专家经验，因此局限性也很大。

（3）不依赖模式描述信息，基于非表达信息的模式匹配方法。比如Kang和Naughton提出了基于互信息（mutual information，MI）的模式匹配方法[13]，并在文中首次将数据模式匹配问题分为one-to-one mapping、onto mapping和partial mapping这3种情形，同时提出了欧式距离和规范化距离两种量度计算模式之间的相似性，后来又提出了适用于该方法的无监督值映射方案[14]。Jaiswal等人提出了计算有序列取值分布PMF（probability mass function）的模式匹配方法[15]，虽然给出了基于有序PMF的值映射方法，但当遇到速度、税率等实数取值的列之间匹配问题时，由于PMF趋近均匀分布，会出现准确率大幅下降的问题。

本文正是在Kang和Naughton提出的基于互信息匹配方法的基础上，提出了一种全新的互信息无向图结点匹配方法。实验结果表明，本文方法能够显著提高模式匹配的准确率，并能够降低匹配花费时间。本文的主要贡献有：

（1）结合互信息依赖矩阵，提出了一种基于有序互信息的无向图结点匹配方法。

（2）改进了文献[12]提出的基于有序PMF的匹配方法，并用于解决无向图结点匹配过程中出现的互信息量度失效问题。

2 相关概念

2.1 可表达匹配和不可表达匹配

Kang和Naughton给出了可表达（interpreted）和不可表达（un-interpreted）信息匹配的基本概念。假定源模式S(s1,s2,…,sm)和目标模式T(t1,t2,…,tn)是分别包含m个元素的数据模式和n个元素的数据模式，映射M1和M2是定义在模式S和模式T上的同一个模式匹配算法的两个匹配结果，匹配算法的定义如下，假定：

式中，fi是任意应用到目标模式T的第i列所有值上的一个一对一函数，那么当且仅当无论 fi的定义如何，M1与M2都完全相同时，称该匹配算法match是一个不可表达匹配方法。反之，称该算法是一个可表达匹配方法。

2.2 元素匹配与结构匹配

元素匹配考虑的是单个列的特征，如列名、类型、取值分布、信息熵等。结构匹配在设计相似度时优先考虑列之间的关系特征，比如外键依赖、互信息等。

2.3 模式匹配算法分类

根据匹配信息是否可表达以及设计相似度目标函数时考虑的粒度，可以将当前的匹配算法分为4个类型，每个类型都有一些已经提出的典型的数据模式匹配算法。匹配算法分类如图1所示。

非可表达的结构匹配方法由于特征直接从数据样本中提取，且在寻找模式的元素之间匹配关系时除了考虑单个列的特征外，还考虑了模式内元素间关系，因此这类算法能够适应多种场景，并且一般能获得较高的匹配准确率。Kang和Naughton提出的方法[10]就属于基于非可表达信息的结构匹配方法的一种。本文提出的方法也属于这一类。

Fig.1 Classification of schema matching algorithms图1 数据模式匹配算法分类

3 基于有序互信息的模式匹配算法

3.1 算法主要流程

基于互信息的模式匹配算法主要分为两步：

步骤1根据源模式S和目标模式T的数据样本求出两个互信息依赖矩阵MS和MT。

步骤2将互信息矩阵MS和MT分别看作带权无向图G1和G2的邻接矩阵，从而将模式匹配问题转化为寻找G1和G2中各个结点的最佳映射关系问题。

互信息矩阵的计算方法和寻找互信息无向图中结点的最佳映射的方法将在后面的章节中详细介绍。

3.2 互信息矩阵的计算方法

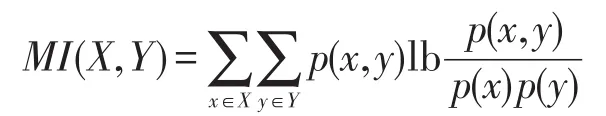
对于待匹配的两个数据模式S(s1,s2,…,sm)和T(t1,t2,…,tn)来说，根据上式求得的MI(si,sj)将作为数据模式S对应的互信息矩阵MS第i行第 j列的元素pij，求解完成后将会得到一个m维对称矩阵，如下所示：

假定属性列X和Y包含在任意一个模式S中，其中模式S的数据样本sampleS中属性列X和Y的独立取值集合分别为X和Y，那么依据样本sampleS可以求得列X与列Y之间的互信息为MI(X,Y)，其中：

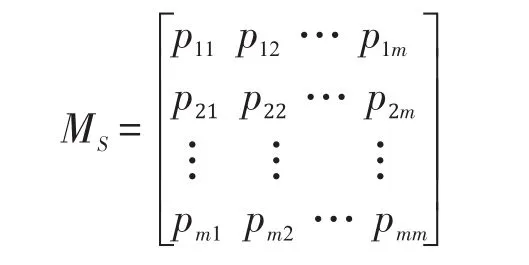
用同样的方法也可以求得数据模式T对应的互信息矩阵MT。

3.3 基于有序互信息的无向图匹配

按照3.2节提到的方法可以分别求得源模式S和目标模式T对应的互信息矩阵MS和MT，将MS和MT分别视为带权无向图G1和G2的邻接矩阵，此时基于互信息的模式匹配问题转换为求两个带权无向图结点最佳匹配问题。若假定m＜n，匹配两个分别包含m个结点和n个结点的带权无向图，则该问题属于onto mapping问题，搜索空间大小为O(m!/(n-m)!)。同样地，若假定m=n,那么该问题就属于one-to-one mapping问题，搜索空间大小是O(n!)。由于one-toone mapping是onto mapping模式匹配问题的常见情形，并且前者是后者的子问题，故本文只针对one-toone mapping问题给出一种全新的无向图结点匹配方法。若解决了one-to-one mapping问题，onto mapping问题可以通过先在属性列个数较多的数据模式中确定一个和另一个数据模式属性列数目相等的属性子集，然后将问题转化为one-to-onemapping问题来解决。

3.3.1 基于互信息启发式无向图结点匹配算法

Kang和Naughton在实验中使用了穷举搜索算法，同时使用启发信息减少搜索空间。这种方法实质就是根据信息熵从无向图G2中筛选出一个包含k个结点的候选子集作为无向图G1中结点i的候选匹配结点。这样的思路很容易理解，通过信息熵可以过滤掉那些与无向图G1中结点i信息熵差距较大的结点，从而在一定程度上减少了搜索空间。

这样的方法虽然思路比较简单，但缺点也是显而易见的。首先，尽管限定了搜索空间，但该方法的搜索空间依然很大，以k=3且n=20为例，此时整个匹配算法搜索空间仍然约达到，因此采用这种方法匹配结点依然需要花费很长时间[12]。当数据模式中包含的属性列数目增加时，该方法的搜索空间变得非常庞大，得出匹配结果花费的时间将变得不可接受。其次，启发信息的获得需要建立在对特定领域数据特征有充分了解的基础上，需要一定的专业知识。最后，由于该方法使用信息熵过滤掉与匹配目标熵值差异较大的结点，在数据模式中各个列在样本信息熵分布比较稀疏时是有效的，但是考虑一些极端情况，比如当数据模式中各个属性列样本信息熵分布比较密集时，所有属性列的信息熵分布在一个较狭窄的区间内，此时采用信息熵过滤机制出错的概率将急剧增大，从而匹配准确率出现明显下降。

3.3.2 基于有序互信息无向图结点匹配算法

正因为基于启发信息匹配方法存在性能和准确率方面的问题，本文给出一种基于有序互信息的无向图结点匹配算法（ordered mutual information graph match algorithm，OMIGM）。

算法1OMIGM(MS,MT)算法

输入：两个无向图G1和G2分别对应的两个互信息依赖矩阵MS和MT。

输出：图G1和G2结点之间的最佳对应关系。1.分别筛选出图G1和G2中剩余待匹配结点

2.以有序互信息欧式距离作为相似量度，依次寻找图G1中各个待匹配结点在图G2的待匹配结点中的最相似的结点，将单向相似关系存入关系集R1中

3.用步骤2中的方法，可以依次求得图G2中各个待匹配结点在图G1待匹配结点中的最相似结点，将单向相似关系存入关系集R2中

4.合并R1和R2，得到双向相似关系集Rdouble，在Rdouble中每个双向关系表示产生了一对新的双向相似关系，并分别从图G1和图G2中移除双向相似关系的关联结点

5.If步骤4中是否产生新的双向相似关系

Then跳到步骤1继续匹配

Else

利用改进的有序PMF方法匹配G1和G2中剩余的未匹配结点

End if

3.3.3 OMIGM算法中使用的相似量度

本小节主要介绍本文提出的基于互信息的无向图结点间相似度的度量方法。在上文介绍的OMIGM(MS,MT)算法中提到了需要根据有序互信息欧式距离在G2中寻找与G1最相似的结点的方法。假定要计算G1中结点n1和G2中结点n2之间的相似度，可以从互信息矩阵中很容易发现以下两点知识：

首先，G1中结点n1与G1中的其他结点之间的互信息对应于互信息依赖矩阵MS的第n1行各元素，记作向量MS,n1。

其次，G1中结点n1与G2中结点n2之间的相似度

可以用向量MS,n1与MT,n2之间的欧式距离来表示。

记G1中结点n1与G2中结点n2之间的相似度为Simn1,n2，那么有：

其中，Simn1,n2是一个非负数，用它可以作为图G1中的结点n1与图G2中的结点n2之间的相似度。

3.3.4 基于有序互信息的无向图结点匹配中发生的“死锁”问题

OMIGM算法的详细流程，其本身并不复杂，但仍有一些细节值得分析。在该匹配算法中当没有找到G1和G2新的结点匹配对时会跳出匹配过程，执行下面改进的有序PMF方法来匹配G1和G2中剩余的未匹配结点。之所以这么做，是因为在匹配过程中可能会出现以下4种情形，如图2所示。图中，橙色代表G1→G2方向的单向映射；黑色代表G2→G1方向的单向映射；绿色代表G1↔G2双向映射。

Fig.2 “Deadlock”state in nodes matching process图2 图结点匹配中出现的“死锁”状态

在采用有序互信息方法进行无向图匹配中可能会出现4种情况，即正常状态、可优化状态、部分“死锁”状态和完全“死锁”状态。正常状态是指G1中的结点和G2中的结点之间互为最近结点，所有结点间呈现一一对应关系，如图2（a）所示。可优化状态是指在某一确定方法的单向映射关系中，存在一对多映射的情形，如图2（b）所示，由于这种情况重新指派映射关系解决，故称为可优化状态。如在图2（b）中可以将结点s2到t2的映射重新指派为s2到t3。在OMIGM算法中通过继续迭代使处于可优化状态的结点继续进行下一次迭代过程。部分“死锁”和完全“死锁”状态是指在无向图结点过程中出现G1和G2中两个结点子集之间的所有映射构成一个环形回路，此时基于互信息的量度已经失效，需要重新考虑其他特征匹配模式G1中剩余结点和模式G2中剩余结点，如图2（c）和图2（d）所示。

3.3.5 图结点匹配过程“死锁”问题的解决办法

本小节介绍一种基于改进的有序PMF方法解决上文提到的“死锁”问题。Jaiswal等人提出了基于有序列取值分布PMF的模式匹配方法[12]，该方法能够在模式匹配中同时完成列匹配和列值映射过程，给不同编码的数据源集成提供了全新思路。但该方法也存在明显的缺陷，比如通过比较两个列取值的PMF获得两列相似性的方法，其实质是计算两个向量欧式距离，因此当取值较多的列匹配时难免会出现高维向量间欧式距离失效问题，影响匹配准确率。

针对上述问题，本文对Jaiswal等人提出的基于有序列取值分布PMF匹配方法进行了改进，按照样本中属性列的独立取值的个数占总样本个数的比例min_percent，将数据模式中的所有属性分为两大类，即离散型属性列和连续型属性列，两种类型的属性采用了不同的匹配方法。对于独立取值较少的离散型属性列，如性别、年龄等，采用Jaiswal等人提出的方法进行匹配；对于连续型属性，如取值为实数的速度、高度等属性，假定这些列的样本取值服从高斯分布，利用极大似然方法估计分布均值和方差，利用分布参数相似性来表达连续型属性列之间的相似程度。一般将min_percent设置为30%即可。

4 验证分析

4.1 实验设计

为了计算数据模式匹配算法的准确性，本文从数据集中依次抽取k个属性，并将第k次抽取的属性记作 ck，由 c1、c2直到ck构成数据模式 S(c1,c2,…,ck),将数据模式S中各个属性列次序随机打乱构成模式T(cq1,cq2,…,cqk)，其中序列 q1,q2,…,qk是随机打乱后的次序。从数据集两个模式的样本中抽取两个相同数量的样本作为输入，在假定不知道列名的情况下，寻找模式S和T的列之间的最佳对应关系，最后通过验证S和T中存在对应关系的属性列的列名是否相同，从而统计出匹配的准确率。在实验中数据模式大小（即包含在数据模式中的属性列数目）从2依次增加到30，同一数据模式大小的匹配实验重复50次，求得平均准确率。为证明本文提出的基于有序互信息的模式匹配算法（OMIGM）的有效性，将该算法实验结果与Kang和Naughton提出的方法（MI-Heuristic）在两个数据集上进行比较。

4.2 相关数据集

本文在实验中使用了Census2000数据集（ftp://ftp2.census.gov/census_2000/datasets/）和 Loans数据集（https://www.lendingclub.com/info/download-data.action）作为测试数据集。Census2000数据集是美国联邦统计局2000年的全美人口信息统计结果，按照各州进行组织，本实验中用到了加州和纽约的统计数据，即CensusCA和CensusYK部分的数据作为实验数据，其中包含112个属性，共计13 696条记录。实验中使用到的另一个数据集是Loans数据集，它来自美国在线个人信贷网站Lending Club 2015年的全年数据，其中包含账户信息、借贷信息等105个属性，共计421 094条记录。由于这些样本中存在不少缺值情况非常严重的属性列，需要根据信息熵过滤掉部分熵值过低（熵值不超过1）的属性列。过滤后的结果如表1所示。

Table 1 Size of datasets表1 数据集的大小

4.3 实验结果及分析

4.3.1 在不同样本集上的实验结果

当样本数目为10 000，实验次数为50时，本文提出的有序互信息图结点匹配方法（OMIGM）与之前提出的基于互信息启发式无向图结点匹配方法（每步匹配候选结点数为3）分别在Census2000数据集和Loans数据集上的实验结果对比如图3和图4所示。

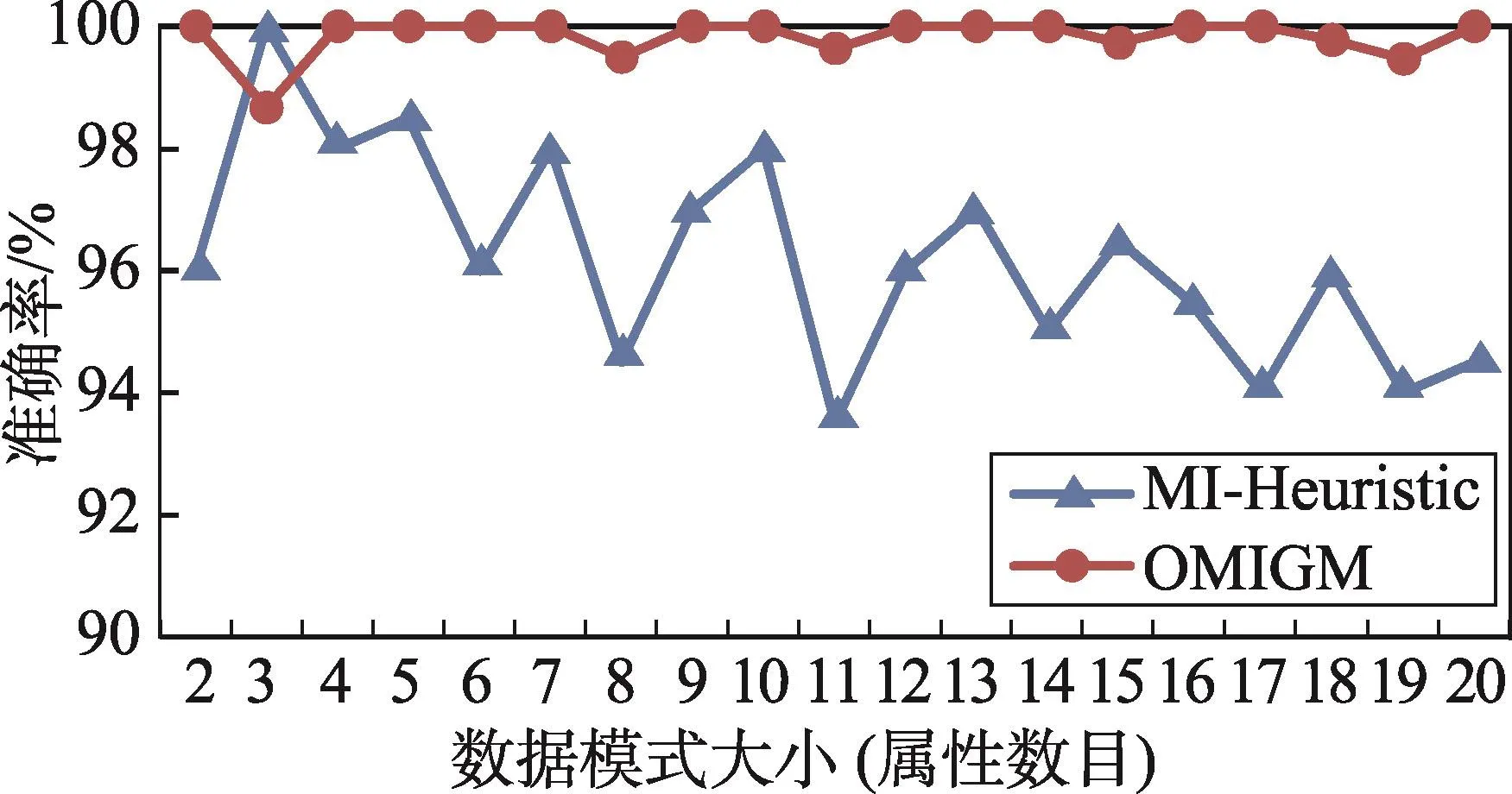
Fig.3 Experiment result in Census2000 dataset图3 在数据集Census2000上的实验结果

Fig.4 Experiment result in Loans dataset图4 在数据集Loans上的实验结果

从图3和图4中可以看出，在两个数据集上，基于有序互信息图匹配方法不仅在准确率方面较基于互信息欧式距离启发式匹配方法有比较明显的提高，而且在识别的稳定性方面也优于后者，即使在属性数目增加到20个时仍有接近94%的准确率。基于互信息的欧式距离启发式匹配方法中匹配的准确率在很大程度上依赖于每步匹配时考虑的候选匹配列的数目k（与当前结点信息熵最接近的k个属性列作为候选匹配列），极端情况下当数据模式的所有属性列在样本中信息熵分布比较接近时，准确地使候选列集合中包含正确的匹配列将变得愈发困难，故当数据模式中包含的属性列数目增加时，匹配准确率呈现比较明显的下降趋势。本文方法由于在考虑候选列时不只依赖信息熵，还依赖于当前列与模式中其他列之间的依赖关系，即使遇到属性列多且信息熵分布比较密集的情况下仍能找到正确的匹配列，即使数据模式中的属性列数目增加，本文方法的匹配准确率也没有出现明显的下降趋势。

4.3.2 算法的运行时间比较

为比较本文提出的有序互信息无向图结点匹配方法（OMIGM）与之前提出的基于互信息启发式无向图结点匹配方法在运行时间方面的差异，在同一数据集Census2000上对两种方法的运行时间进行了统计，数据模式大小从2依次增加到14，每个数据模式大小做20次实验求得平均运行时间。但考虑到单机环境下启发式匹配方法在属性个数增加到14时运行时间已经变得无法接受，故将数据模式大小增加到14时终止。统计结果如图5所示。

Fig.5 Statistical result of running time图5 运行时间统计结果

从图5中可以看出，当数据模式中属性列个数超过10后，启发式算法匹配需要花费的时间呈现出指数增长，而本文方法花费的时间比前者少得多，而且随着属性个数增加，运行时间并没有出现较大增长。事实上，当属性个数超过50时，本文基于有序互信息的匹配方法的运行时间也是小时级。

4.3.3 数据集中信息熵分布对结果的影响

为了分析不同样本对本文提出的基于有序互信息无向图结点匹配准确率的影响，在实验中统计了Census2000和Loans两个数据集在经过过滤后剩余所有属性的信息熵。统计结果如图6和图7所示。

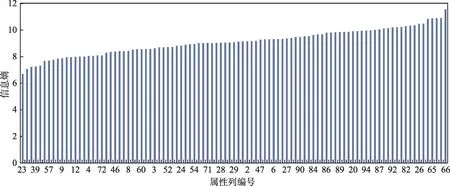
Fig.6 Statistical result of information entropy in Census2000 dataset图6 Census2000数据集信息熵统计结果

通过对比图6和图7中的统计结果可以看出，Loans数据集中所有属性列的信息熵分布比Census-2000数据集分布更加分散。从统计图中可以明显看出，Census2000数据集中大部分属性列的信息熵集中在区间6到8之间，反观Loans数据集中有接近一半的属性列的信息熵集中在4到6之间。信息熵反映的是属性列中蕴含的信息量大小，由此可见Loans数据集中信息总量要明显少于Census2000数据集，这就解释了两种匹配方法在Loans数据集上的匹配准确率明显低于其在Census2000数据集上的准确率，这点从图3和图4的结果中可以看出。

4.3.4 样本数量对结果的影响

为了评估样本大小对实验结果的影响，本文从Loans数据集中抽取3个样本数量分别为1 000、5 000和10 000的样本。数据模式中属性列数目从2增加到10，每个数据模式大小样本各抽样10次，求样本的平均差异度。样本的差异度是指每次抽取的模式数据样本统计得来的两个互信息依赖矩阵中所有元素的差的平方和。统计后的结果如图8所示。

Fig.7 Statistical result of information entropy in Loans dataset图7 Loans数据集信息熵统计结果

Fig.8 Statistical result of average diversity图8 样本平均差异度统计结果

从图8中的统计结果可以看出，随着模式中属性数量的增加，平均样本差异度也呈现很明显的上升趋势。但是显然当样本数量为10 000时，平均差异度的上升趋势较为平缓，这就表明在进行模式匹配时，模式S和模式T各自对应的互信息矩阵MS和MT之间的差异相较于1 000和5 000样本时的差异要小一些，从而减少了因样本差异引起的错误匹配情况的发生。当然，样本数量越大平均差异度越小，但同样会导致计算互信息依赖矩阵时花费的时间变长。综合考虑以上因素后，在本文的实验中采用10 000作为样本大小进行模式匹配。

5 结论

本文提出了一种基于有序互信息的数据模式匹配方法，其通过对列之间的互信息进行排序将全局优化问题降为局部优化问题，通过寻找双向匹配提高了匹配结果的可靠性。当出现“死锁”情形时，利用改进的有序PMF方法匹配发生“死锁”后的剩余属性列，进一步提高了匹配的准确率。通过在两个数据集上对比基于有序互信息的图匹配方法和基于互信息的启发式匹配方法的实验结果，证明了本文方法不仅在匹配准确率和算法耗时等方面都明显优于后者，而且具有更好的通用性。

[1]Bernstein PA,Madhavan J,Rahm E.Generic schema matching,ten years later[J].Proceedings of the VLDB Endowment,2011,4(11):695-701.

[2]Bilke A,Naumann F.Schema matching using duplicates[C]//Proceedings of the 2005 International Conference on Data Engineering,Tokyo,Apr 5-8,2005.Piscataway,USA:IEEE,2005:69-80.

[3]Embley D W,Jackman D,Li Xu.Multifaceted exploitation of metadata for attribute match discovery in information integration[C]//Proceedings of the 2001 International Workshop on Information Integration on the Web,Rio de Janeiro,Apr 9-11,2001:110-117.

[4]Madhavan J,Bernstein P A,Rahm E.Generic schema matching with cupid[C]//Proceedings of the 27th International Conference on Very Large Data Bases,Roma,Italy,Sep 11-14,2001.San Francisco,USA:Morgan Kaufmann Publishers Inc,2001:49-58.

[5]Li W S,Clifton C.SEMINT:a tool for identifying attribute correspondences in heterogeneous databases using neural networks[J].Data&Knowledge Engineering,2000,33(1):49-84.

[6]Berlin J,Motro A.Database schema matching using machine learning with feature selection[C]//LNCS 2348:Proceedings of the 2002 International Conference on Advanced Information Systems Engineering,Toronto,Canada,May 27-31,2002.Berlin,Heidelberg:Springer,2002:452-466.

[7]Bernstein P A,Melnik S,Petropoulos M,et al.Industrialstrength schema matching[J].ACM SIGMOD Record,2004,33(4):38-43.

[8]Drumm C,Schmitt M,Do H H,et al.Quickmig:automatic schema matching for data migration projects[C]//Proceedings of the 16th Conference on Information and Knowledge Management,Lisbon,Portugal,Nov 6-10,2007.New York:ACM,2007:107-116.

[9]Do H H,Rahm E.COMA:a system for flexible combination of schema matching approaches[C]//Proceedings of the 28th International Conference on Very Large Data Bases,Hong Kong,China,Aug 20-23,2002:610-621.

[10]Algergawy A,Massmann S,Rahm E.A clustering-based approach for large-scale ontology matching[C]//LNCS 6909:Proceedings of the 2011 East European Conference on Advances in Databases and Information Systems,Vienna,Austria,Sep 20-23,2011.Berlin,Heidelberg:Springer,2011:415-428.

[11]Rodrigues D,da Silva A S,Rodrigues R,et al.Using active learning techniques for improving database schema matching methods[C]//Proceedings of the 2015 International Joint Conference on Neural Networks,Killarney,Ireland,Jul 12-17,2015.Piscataway,USA:IEEE,2015:1-8.

[12]Ferragut E,Laska J.Nonparametric Bayesian modeling for automated database schema matching[C]//Proceedings of the 14th IEEE International Conference on Machine Learning and Applications,Miami,USA,Dec 9-11,2015.Piscataway,USA:IEEE,2015:82-88.

[13]Kang J,Naughton J F.On schema matching with opaque column names and data values[C]//Proceedings of the 2003 International Conference on Management of Data,San Diego,USA,Jun 9-12,2003.New York:ACM,2003:205-216.

[14]Kang J,Lee D,Mitra P.Identifying value mappings for data integration:an unsupervised approach[C]//Proceedings of the 2005 International Conference on Web Information Systems Engineering,New York,Nov 20-22,2005.Berlin,Heidelberg:Springer,2005:544-551.

[15]JaiswalA,Miller D J,Mitra P.Un-interpreted schema matching with embedded value mapping under opaque column names and data values[J].IEEE Transactions on Knowledge&Data Engineering,2009,22(2):291-304.

GUO Lele was born in 1990.He is an M.S.candidate at School of Computer and Information Technology,Beijing Jiaotong University.His research interests include algorithm design and data integration,etc.

郭乐乐（1990—），男，陕西西安人，北京交通大学计算机与信息技术学院硕士研究生，主要研究领域为算法设计与分析，数据集成等。

林友芳（1971—），男，福建武平人，北京交通大学计算机与信息技术学院副院长、教授、博士生导师，主要研究领域为大数据技术，商业智能等。

HAN Sheng was born in 1980.He received the M.S.degree from Beijing Jiaotong University in 2005.Now he is a lecturer at School of Computer and Information Technology,Beijing Jiaotong University.His research interests include software engineering and data housing,etc.

韩升（1980—）男，山西长治人，2005年于北京交通大学获得硕士学位，现为北京交通大学计算机与信息技术学院讲师，主要研究领域为软件工程，数据仓库等。

Using Ordered Mutual Information to Match Schema with Opaque Column Names and Data Values*

GUO Lele+,LIN Youfang,HAN Sheng
Beijing Key Laboratory of Traffic Data Analysis and Mining,School of Computer and Information Technology,Beijing Jiaotong University,Beijing 100044,China

As a key issue of data integration,schema matching is the core task in data merging process of heterogeneous data sources.At present,a mass of schema matching methods have been proposed.However,most of them are lack of universality since they depend on the description information of schema heavily.Therefore,it is difficult to apply these approaches to other scenarios.To solve the problem,this paper proposes a novel schema matching method which uses ordered mutual information and does not rely on any description information of schema,such as column name,column type and foreign constraints,which make it own a strong universality.Furthermore,extensive experiments on various datasets indicate that the proposed technique outperforms earlier schema matching methods in terms of efficiency and accuracy.

schema matching;opaque conditions;mutual information;undirected graph matching

the Ph.D.degree from Beijing Jiaotong University.He is a professor and Ph.D.supervisor at School of Computer and Information Technology,Beijing Jiaotong University.His research interests include big data technology and business intelligence,etc.

2016-08, Accepted 2016-10.

A

TP391.4

+Corresponding author:E-mail:guolele@bjtu.edu.cn

GUO Lele,LIN Youfang,HAN Sheng.Using ordered mutual information to match schema with opaque column names and data values.Journal of Frontiers of Computer Science and Technology,2017,11(9)：1389-1397.

10.3778/j.issn.1673-9418.1609004

*The National Natural Science Foundation of China under Grant Nos.61403023,61603029(国家自然科学基金);the Research Fund of Ministry of Education-China Mobile under Grant No.MCM20150513(教育部-中国移动科研基金);the Fundamental Research Funds for the Central Universities of China(中央高校基本科研业务费专项资金).

CNKI网络优先出版: 2016-10-31, http://www.cnki.net/kcms/detail/11.5602.TP.20161031.1650.016.html