基于多层次模糊综合评判机制的高校学生综合素质测评的应用

司 瑾



基于多层次模糊综合评判机制的高校学生综合素质测评的应用

司 瑾

（长春工程学院 吉林 长春 130012）

综合素质测评，是推动素质教育的切入点。建立一套适合高校学生的综合素质测评体系对提高学生综合素质，提高教学效益具有重要意义。本文运用多层次模糊综合评判机制，可保证定性指标向定量的科学转化，使评价具有客观性、科学性和适用性。

模糊评判；综合素质

前言

实施素质教育，是高等教育的一项系统工程，实施素质测评本身，对大学生的成长成才具有导向和激励作用；对大学生思想政治教育，起规范和促进作用；同时，对用人单位的人才选聘，也有重要的参考作用。本文针对这种信息不确定、判断依据不绝对的情况，在测评中引入模糊综合评判技术，对于不确定的因素采用隶属度予以描述，以实现从定性到定量的转化。面对综合素质测评所要考虑的因素较多，对各因素的权重区分较为困难时，采用二级或多级评判，进行多层次的模糊综合评判，使测评更加公正合理。

1 建立高校学生素质测评的模糊评判指标体系

测评指标选取的合理性是决定一个测评方法是否成功的关键。大学生综合素质测评的模糊评判以确定测评方案开始，根据测评的目的、范围、测评时限、信息采集的范围和方式等，确定评价因素、评价因素的权重、评定等级。

1.1 评价因素的确定

为建立科学严谨、全面细致、完善有序的评判指标体系，考量综合素质所包含因素较多，并咨询教学管理部门、学生管理部门及就业指导中心，得到思想素质、科学素质、人文素质和身心素质4个一级指标，并按一定规则进行分类，形成了16个二级指标，即采用多级指标体系。

设定高校学生综合素质为U，其指标体系构建如表1：

表1 高校学生综合素质指标体系

各层次因素指标集：

U={U1,U2,U3,U4} U1={U11,U12,U13,U14} U2={U21,U22,U23,U24} U3={U31,U32,U33,U34} U4={U41,U42,U43,U44}

1.2 评价因素权重的确定

权重的确定反映了不同的评价偏好，因而不同的综合评价项目体现出不同的评价目的和导向。根据每一层各个因素在高校学生综合素质测评中所起的作用和重要程度不同，分别给每一个因素赋以相应的权重。

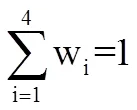
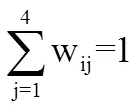
1.3 评定等级的确定

假设评定等级分为：优、良、中、差4个等级，构成评语集V={V1,V2,V3,V4}。

2 建立多层次模糊综合评判模型

2.1 模糊评价集的确定

由学工办、辅导员、任课教师和学生会干部组成N人评价小组，对16个二级指标进行评价，用模糊统计方法确定模糊评价集。设评价小组评估出第二层某因素Uij为优、良、中和差的人数分别为X1，X2，X3，X4，则该因素的模糊评价集为

Rij={}={rij,1,rij,2,rij,3,rij,4} …………………………………………(1)

则一级指标Ui的模糊评价集为

Ri= .......................................................(2)

2.2 一级模糊综合评判

一级模糊综合评判是对一级指标Ui的加权测评。设Yi为Ui的一级评判向量，则有：

Yi=Wi·Ri={yi1,yi2,yi3,yi4} ………………………………………………(3)

其中，yij=，yi1,yi2,yi3,yi4分别表示对因素Uij的评价结果属于V1,V2,V3,V4的隶属度（i=1,2,3,4）。

2.3 二级模糊综合评判

根据一级模糊综合评判向量，得到的二级评判矩阵为：

Y=…………………………………………………………………………(4)

2.4 综合评判向量的确定

按照权重的分配，从U→V上的综合评判向量为：

Z=W·Y=(z1,z2,z3,z4)，其中，……………………………………………(5)

2.5 综合评判向量归一化

综合评判向量的处理需要考虑所有指标的贡献，因而采用加权平均法，在评判对象是定性指标是，先将评判集中元素量化，即V1=4，V2=3，V3=2，V4=1，再将Z归一化Z’：

Z’=………………………………………………………………………(6)

于是，评判结果P=Z’·VT(T表示矩阵转置)，P值越接近4，说明综合素质越高，越接近1，说明综合素质越低。

3 模糊综合评判实例应用

对某高校一位学生综合素质进行评价，经专家和调查表对其因素进行评判，得到如下权重向量指标权重确定为：

W=(0.2,0.3,0.3,0.2), W1=(0.3,0.3,0.2,0.2), W2=(0.3,0.2,0.3,0.2), W3=(0.2,0.3,0.3,0.2), W4=(0.3,0.3,0.3,0.1)

评语集V={V1,V2,V3,V4}对16个指标进行投票评定，各指标分为优、良、中、差4个等级，将所得数据带入公式（1）（2）后，得到一级评判隶属矩阵为：

R1= R2= R3= R4=

由（3）式可得出一级评判向量为：

Y1=(0.3,0.3,0.3,0.2)，Y2=(0.3,0.3,0.3,0.1)，Y3=(0.2,0.3,0.3,0.2)，Y4=(0.3,0.3,0.2,0.1)

由（4）（5）（6）式得出综合评价向量并归一化后为：

Z’=(0.3,0.3,0.25,0.15)

最终评判分数为：P=Z’·VT=2.75

由于评判分数比较接近3，因而该学生综合素质属于良。

4 结束语

模糊综合评判法，是把主观模糊评价与客观具体事实结合起来的一种思维方法，也是定性和定量分析相结合的方法。对于综合评判模型的建立，同样具有一定的灵活性，如对重要问题或精密问题，其数据的确定需要专家权威论证。对于一般问题，则以调查讨论确定数据，为评判提供依据。就此模型总体而言，为大学生综合素质评价提供了一种系统、规范、全面的思考方法。大学生综合素质评价是一个多因素的模糊评判过程，多层次模糊综合评判方法克服了学生综合素质指标的不确定性以及各层次之间的边界模糊性问题，大大提高了测评结果的准确性和可信度，是一种具有广泛实用价值的评价方法。

[1]赵健. 模糊综合评判在大学生素质测评中的应用研究[J].教育评论, 2014(10) :38-41.

[2]印丹榕. 高校学生德育水平模糊综合评价研究[J].中国电力教育, 2013(17):139.

[3]尹世群. 基于模糊综合评判推理机制的学生素质评价系统设计与实现[J].计算机应用, 2002(22) :81-83.

[4]尤建成, 强建周. 学生评价——大学素质教育的切入点[J].中国高教研究,2000 (2):43-44.

Comprehensive quality assessment is the starting point of promoting quality education. The establishment of a fuzzy evaluation system for quality assessment in accordance with the characteristics of students in higher vocational education is of great importance to enhancing students all-round development and increasing teaching results. In this paper, a multi-level fuzzy comprehensive evaluation mechanism can be used to guarantee the scientific transformation of qualitative indicators to quantitative science and make the evaluation be objective, scientific and applicable.

fuzzy evaluation; comprehensive quality

10.19551/j.cnki.issn1672-9129.2017.10.003

司瑾，1983年3月出生，性别女，籍贯黑龙江北安，学历：硕士研究生，职称：助理实验师，研究方向：计算机网络安全与数据通信处，邮箱329009965@qq.com。

TP311.52

A

1672-9129(2017)10-0003-01