面板数据分位数回归模型的参数估计与变量选择

何晓霞,徐伟,李缓,吴传菊

(武汉科技大学理学院,湖北武汉430065)

面板数据分位数回归模型的参数估计与变量选择

何晓霞,徐伟,李缓,吴传菊

(武汉科技大学理学院,湖北武汉430065)

本文研究了基于面板数据的分位数回归模型的变量选择问题.通过增加改进的自适应Lasso惩罚项,同时实现了固定效应面板数据的分位数回归和变量选择,得到了模型中参数的选择相合性和渐近正态性.随机模拟验证了该方法的有效性.推广了文献[14]的结论.

面板数据;分位数回归;自适应Lasso;变量选择;渐近正态性

1 引言

近年来,由于计算机技术的日益成熟,分位数回归在理论和方法上都得到了广泛的应用. Koenker[1]首次提出了分位数回归,如今分位数回归作为均值回归分析的稳健替代,被广泛地用于探索响应变量与协变量之间的潜在关系.在实际应用中,分位数回归可以刻画响应变量更多的分布特征.Koenker[2]发现分位数回归的结果可以提供比普通条件均值回归更丰富,更有针对性.特别是,它提供了探索异质性的来源与合作的响应变量一种方法,并深入研究了分位回归模型及其估计.王新宇[3]系统地介绍了分位数的基本模型及其扩展、分位数回归模型的经典统计推断.Tang等[4]研究了加权复合分位数(WCQ)与随机截尾线性回归模型.在这个模型中,提出了可变选择的自适应惩罚程序,并证明了一致性和渐近正态性. Wang和Yin[5]研究了无界意义下的在线变化分位数回归算法.

分位数回归模型中的变量选择问题一直受到广泛的关注.Shows等[6]针对一种多元线性模型,提出了对随机删失数据的自适应Lasso加权LAD(AWLAD)变量选择方法.Wang等[7]提出了BIC调整参数选择方法,证明了这种方法能够辨别出真模型,并在模拟中验证了理论的有效性.Wu等[8]研究了惩罚分位数回归,在一些较弱的条件下得到了SCAD和自适应Lasso惩罚分位数回归的Oracle性质.Zou[9]提出了分位数回归模型的自适应Lasso的变量选择方法,也得到了其Oracle性质.吕亚召等[10]研究部分线性单指标复合分位数回归模型,提出了用自适应Lasso的变量选择方法,该方法用BIC选择最优调整参数,在随机模拟中验证了所提方法的优良性.

相对于横截面或是时间序列数据来说,面板数据含有更多的信息,因此,面板数据回归模型的研究越来越受关注.巴尔塔基[11]提出了面板数据模型及其参数的估计方法,并给出了实际应用.李扬等[12]提出了惩罚似然变量选择问题,证明了面板数据的自适Lasso具有Oracle性质.在选择最优调整参数时,模拟显示BIC和GCV的选择结果一般比AIC有优势.曲婷等[13]对平衡纵向数据模型,通过Lasso方法可将模型的系数压缩到0,采用AIC和BIC准则选取最优参数,从而达到变量选择的目的.Koenker[14]首次提出了面板数据分位数回归模型,用加权的形式控制分位数对效应的影响,并加入l1惩罚项,既保持了线性规划形式,又保持了结果设计矩阵的稀疏性.李翰芳等[15]对随机效应面板数据,通过引入条件Laplace先验,构造了一种新的贝叶斯Lasso分位数回归法,与一般贝叶斯分位回归法相比更有效的将异质变量的系数压缩到0,从而起到变量选择的作用.

分位数回归对误差项的分布没有具体的限制,对异质点或者是非正态分布的参数的估计具有一定的稳健性,将分位数回归和面板数据模型两者结合起来,在控制个体差异的同时,可以分析各种变量在不同分位点之间的关系.基于面板数据的分位数回归模型,本文提出了一种在改进的自适应Lasso的罚函数下对变量进行选择的方法,对系数变量的值进行压缩,使得异质变量的系数为0,从而达到变量选择的效果,并证明了相合性和渐近正态性,在模拟中用验证了选择的有效性.

2 模型与方法

2.1 经典高斯随机效应模型

考虑一般的随机效应面板数据模型

其中yij是因变量,xij是自变量,αi是不可观测的时间不变效应,uij是误差项.写成矩阵的形式如下y=XTβ+Zα+u,其中y是n×1维,X是nm×p维,Z是nm×n维的虚拟变量的关联矩阵,α和u是独立的随机向量.

2.2 加权分位数面板数据模型

令ρτk(u)=u(τk-I(u≤0)),yij的分位数函数为

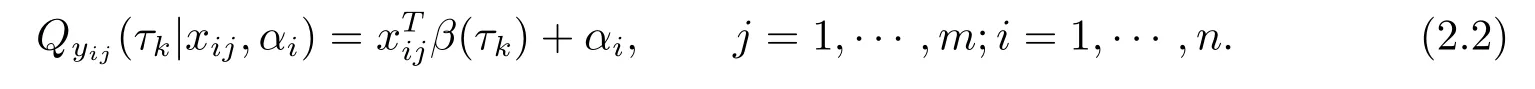
为了更好的估计参数,对(2.1)式提出加权分位数估计方法,

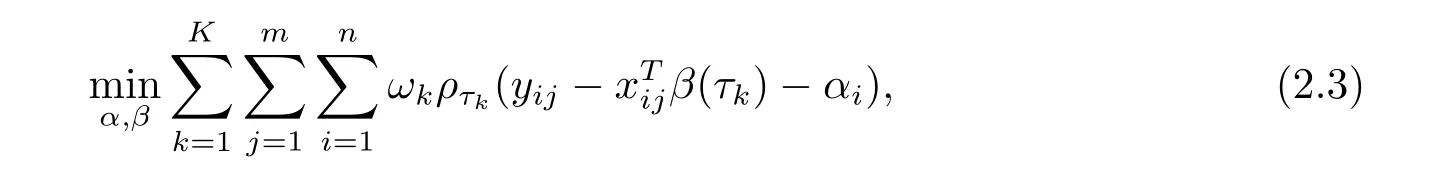
最小化(2.3)是一个凸规划问题,加权分位数回归估计方法可以凸优化来实现.在分位数函数(2.2)中,α与因变量的条件分位数相对应,为了更好的估计截面的分位数方程,Koenker[14]引入了惩罚项代替高斯惩罚项,

3 渐近性质

由于E[I(yij-ξij(τk)＜0)-τk]=0,结合中心极限定理和Cram´er-Word定理,Zn,m,k和Wn,m,k依分布收敛到Zk和W1,其中Zk是一个正态随机变量,均值为0,W1是一个n维正态向量,均值为0.因此可以得到

因此当mn→∞时,

则有

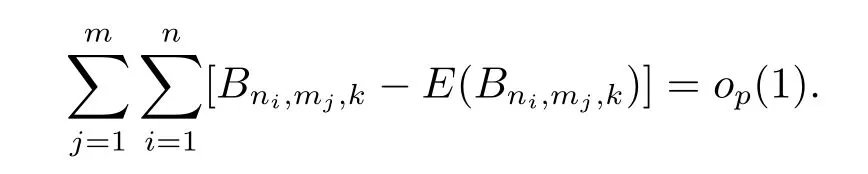
另外,由于

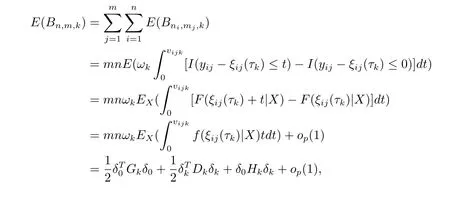
其中

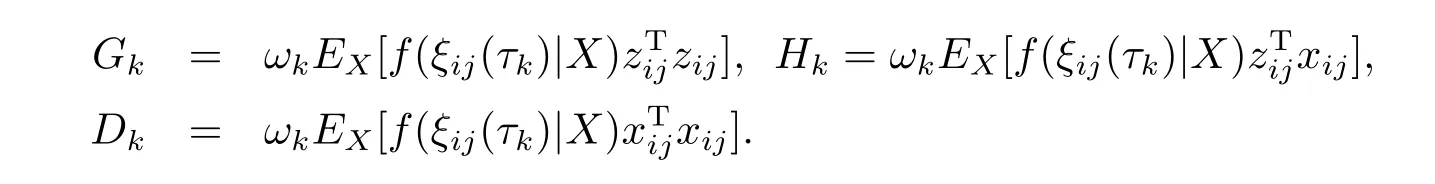
则

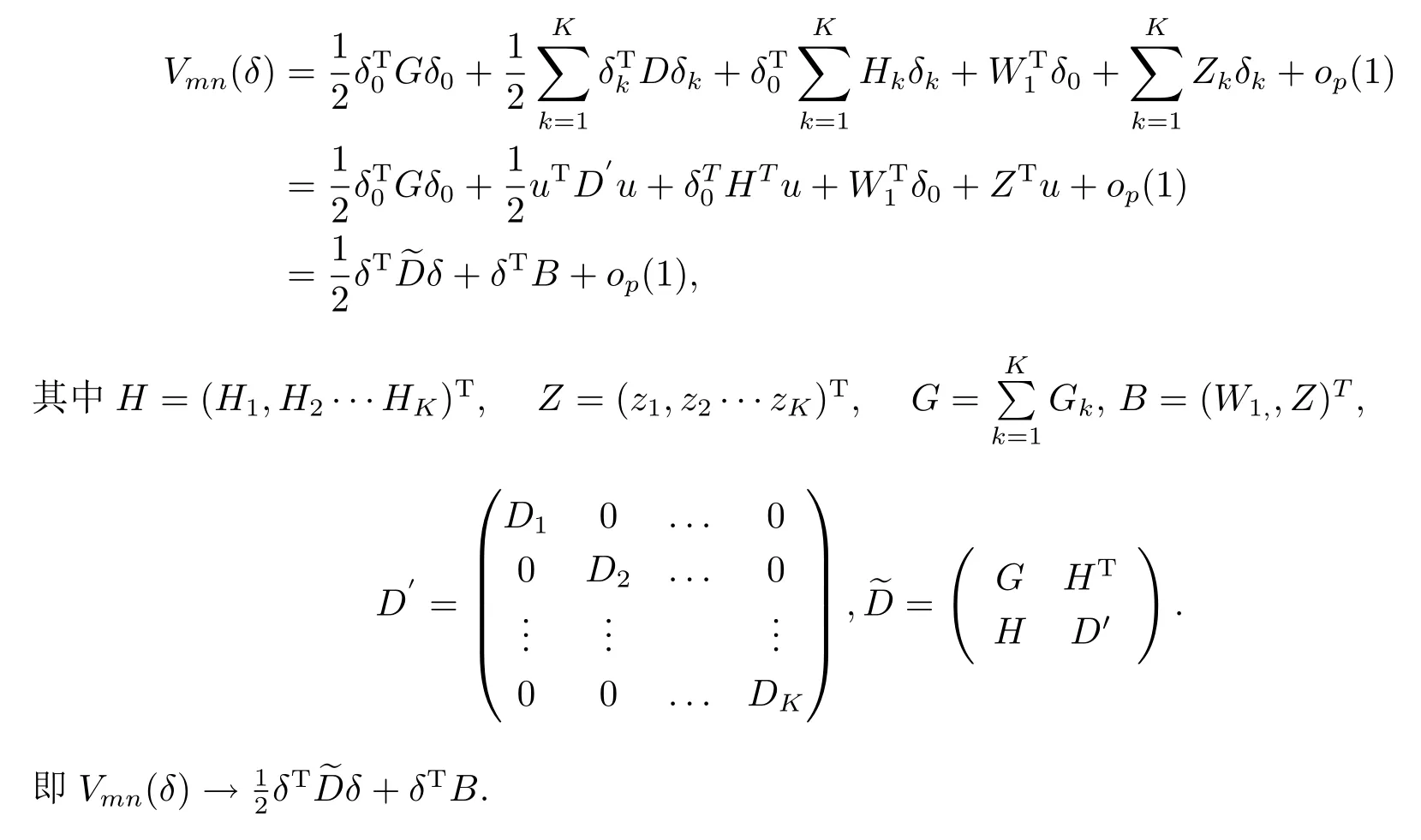
由Koenker[14]中引理1,可以得到˜u→dN(0,D-1ΣD-1).

4 变量选择

在对数据进行统计分析时,人们一般会借助一些相关变量对所关心的变量进行分析,建模,以便得到理想的结果,一般称这些相关的变量为协变量,而所关心的变量为因变量.在开始建模的时候,希望加入更多的相关变量,来得到更真实的结果,然而,随着协变量的增多,异质变量存在的可能性就越大,于是,希望寻找一个有效方法来选出对响应变量有显著影响的协变量.因此变量选择就是统计学中一个重要的问题.本节对上述面板数据分位数模型的变量选择进行分析,在(4.1)式中需要指定调节参数λ2,本文最优的调整参数λ2可以通过BIC (Bayesian information criterion)准则选取.在加权分位数估计的同时,同时希望对变量做选择,本节选的罚函数是自适应Lasso罚函数.令

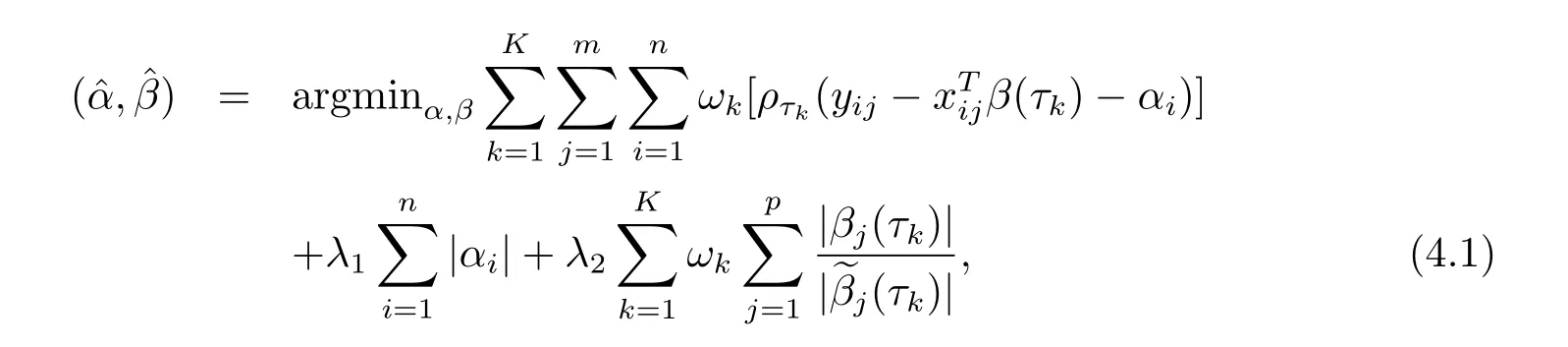
令BIC(λ)=logPλ+dfλ·log(mn)/mn,其中

(i)因为Lmn(δ)是对δ的分段线性函数,在每个可微的点,对k=1,2,···,K,j= q+1,···,p取Lmn(δ)对δkj的偏导,有

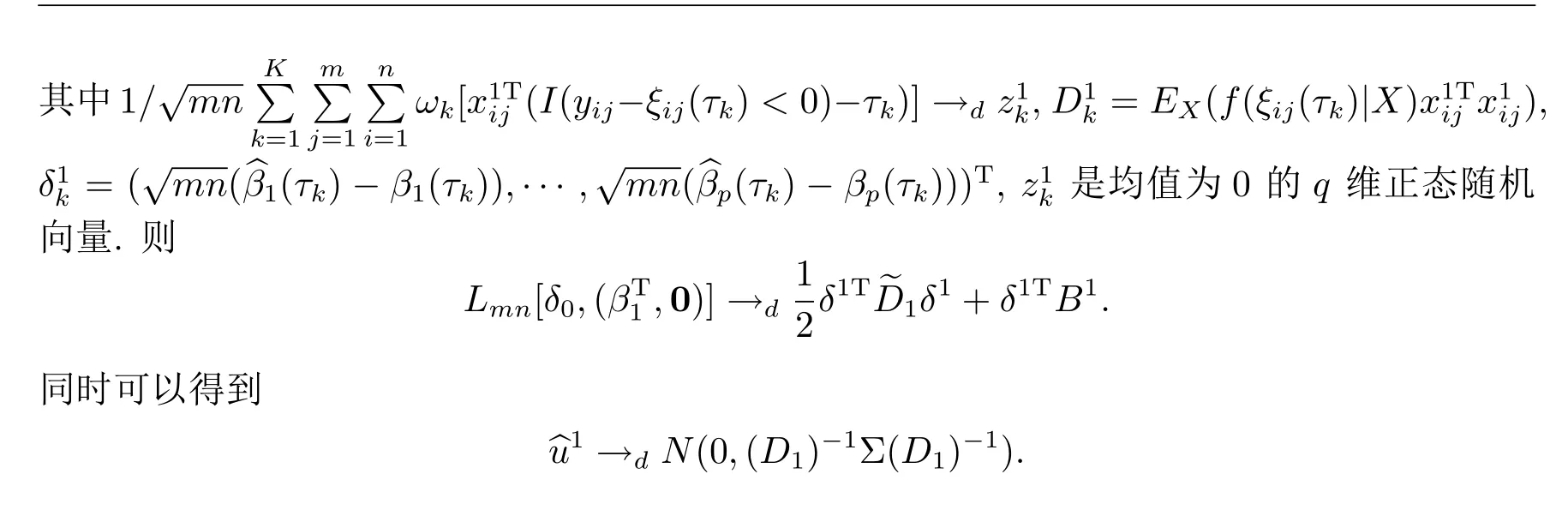
5 随机模拟

在本节给出两个例子,比较不同的方法对参数估计值优势,并验证自适应Lasso罚函数对变量选择的有效性.

例1考虑n=50,m=5,p=1,响应变量由下面的模型生成

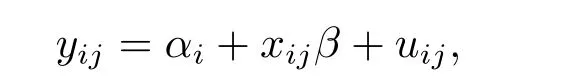
其中β=1,αi和uij服从标准正态分布,ω=(0.25,0.5,0.25)在三个分位点τ=(0.25,0.5,0.75), xij由高斯分布生成

γi和vij独立同分布,相应的组内相关系数,

就是xij和xik之间的相关系数,当j 6=k时,在的模拟中,都令ρx=0.5.而λ1选择位置参数比σu/σα,λ2的选择由上一节BIC得到,α和uij分两种情况.

1.都来自于标准正态;

2.都来自于自由度为3的t分布.

这样可以得到分别在分位数回归的估计方法(QR)、分位数效应罚函数估计(PQR)、分位数回归自适应罚函数估计(LPQR),对β的估计,如表1,可以看出在α和uij的两种情况PQR和LPQR都比QR估计更优.

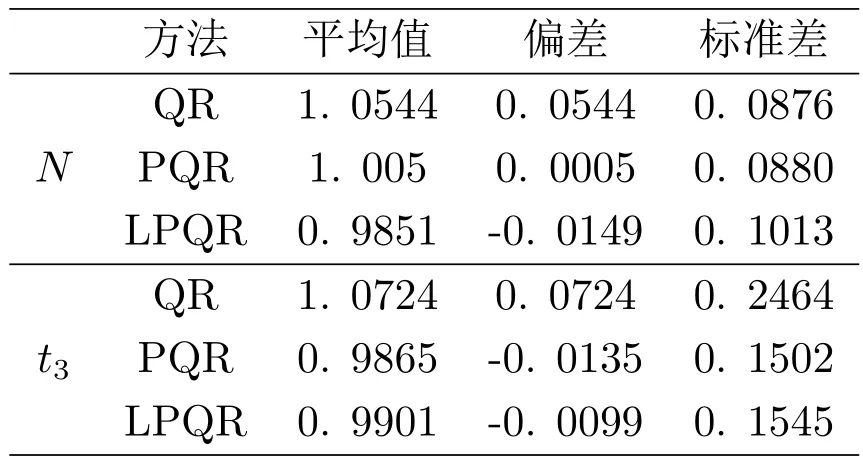
表1：例1中β参数估计

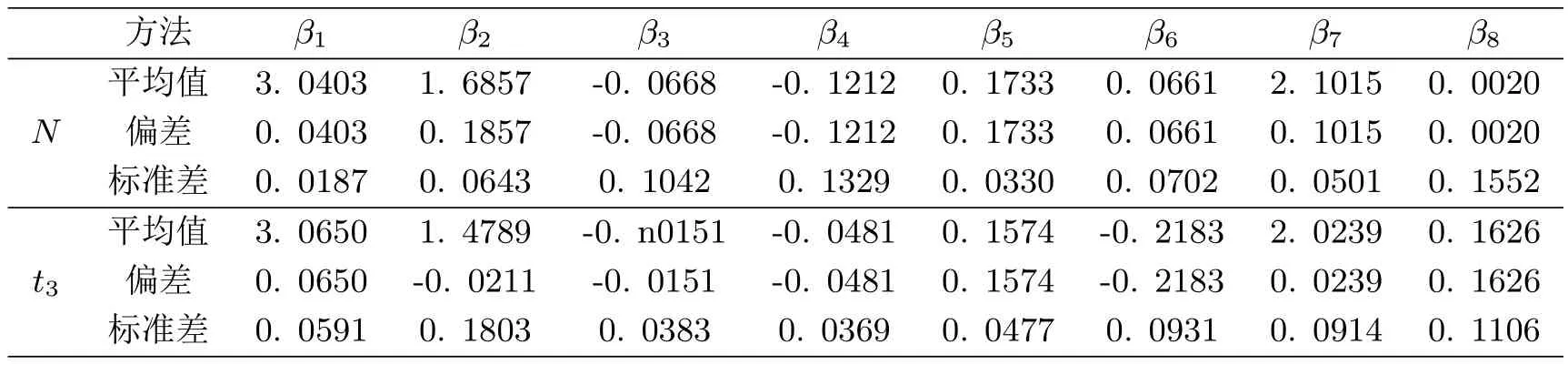
表2：例2中β罚估计

表3：例2中β变量选择

例2令m=5,n=50,p=8,响应变量来自下面的模型

β=(3,1.5,0,0,0,0,2,0),xij由(5.1),(5.2)式生成,αi和uij同样分两种情况.

1.都来自于标准正态;

2.都来自于自由度为3的t分布.

表2是分位数罚估计(PQR)分别对上面两种情形下β的估计,表3是分位数自适应Lasso罚函数(LPQR)对参数的估计,通过模拟可以看出PQR可以对参数做近似估计,但对异质变量不能做选择,而LPQR在参数估计的同时对变量做了选择,0参数都选择出来了,不管是参数估计还是变量选择都比PQR有优势.

[1]Koenker R.Bassett G.Regression quantiles[J].Econo.,1978,46：33-50.

[2]Koenker R.Quantile regression[M].Cambridge：Cambridge University Press,2005.

[3]王新宇.分位数回归理论及其在金融风险测量中的应用[M].北京：经济科学出版社,2010.

[4]Tang L,Zhou Z,Wu C.Weighted composite quantile estimation and variable selection method for censored regression model[J].Stat.Prob.Lett.,2012,3：653-663.

[5]Wang B,Yin H.Varying quantile regression with online scheme and unbounded sampling[J].J. Math.,2015,34：281-286.

[6]Shows H,Lu W,Zhang H.Sparse estimation and inference for censored median regression[J].Stat. Plan.Infer.,2010,140：1903-1917.

[7]Wang H,Li R,Tsai C L.Tuning parameter selectors for the smoothly clipped absolute deviation method[J].Biometrika,2007,94：553-568.

[8]Wu Y,Liu Y.Variable selection in quantile regression[J].Statist.Sinica,2009,19：801-817.

[9]Zou H.The adaptive Lasso and its oracle properties[J].Amer.Stat.Assoc.,2006,101：1418-1429.

[10]吕亚召,张日权等.部分线性单指标模型的复合分位数回归及变量选择[J].中国科学,2014,12：1299-1322.

[11]巴尔塔基.面板数据计量经济分析[M].北京：中国人民大学出版社,2010.

[12]李扬,曾宪斌.面板数据模型的惩罚似然变量选择方法研究[J].统计研究,2014,3：83-89.

[13]曲婷,王静.基于Lasso方法的平衡纵向数据模型变量选择[J].黑龙江大学自然科学学报,2012,29：715-722.

[14]Koenker R.Quantile regression for longitudinal data[J].J.Multi.Anal.,2004,91：71-89.

[15]李翰芳,罗幼喜等.面板数据的贝叶斯LASSO分位回归方法[J].数量经济技术经济研究,2013,2：138-149.

[16]Knight K.Limiting distributions for L1regression estimators under general conditions[J].Ann. Stat.,1998,26：755-770.

PARAMETER ESTIMATION AND VARIABLE SELECTION IN THE QUANTILE REGRESSION MODEL FOR PANEL DATA

HE Xiao-xia,XU Wei,LI Huan,WU Chuan-ju

(College of Science,Wuhan University of Science and Technology,Wuhan 430065,China)

In this paper,we consider the variable selection problem for the quantile regression model based on panel data.By adding an improved adaptive lasso penalty term, we realize the quantile regression and variable selection for the panel data with f i xed ef f ect simultaneously,and obtain the consistency and asymptotical normality for the selection of the parameters.Simulation studies show the validity of the proposed method,which extend that of [14].

panel data;quantile regression;adaptive lasso;variable selection;asymptotic normality

O211.7

A

0255-7797(2017)05-1101-10

2015-09-26接收日期：2016-02-25

国家自然科学基金资助(11201356).

何晓霞(1979-),女,湖北大悟,副教授,主要研究方向：数理统计.

2010 MR Subject Classif i cation：62F12;62J05