FORCING AN ω1-REAL WITHOUT ADDING A REAL
ZHU Hui-ling,ZHENG Fu-dan
(Guangzhou College,South China University of Technology,Guangzhou 510800,China)
FORCING AN ω1-REAL WITHOUT ADDING A REAL
ZHU Hui-ling,ZHENG Fu-dan
(Guangzhou College,South China University of Technology,Guangzhou 510800,China)
In this paper,we study strong Mathias forcing and its generalizations to uncountable cases.By applying the method of forcing,we show that strong Mathias forcing adds unbounded but not dominating reals,which is in contrast to usual Mathias forcing.We also show that the ω1-version of strong Mathias forcing adds unbounded but not dominating ω1-reals and meanwhile, this forcing adds no new reals,which are applied to the consistency of cardinal invariants on the real line.
ω1-real;Mathias forcing;dominating reals;unbounded reals;cardinal invariants
1 Introduction
Forcing is a mechanism of obtaining independent results over the commonly accepted foundation of mathematics,the Zermelo-Fraenkel axiom system with the axiom of choice. Since its formulation by Cohen[1],forcing has become a powerful tool in advanced set theory as well as other related f i elds and proved numerous results.
Roughly speaking,forcing usually works in the following way:to prove that a statement ¬φ is unprovable from ZFC,one builds a model of ZFC together with φ.One starts with a ground model V and force with a generic f i lter G to get a bigger model,the generic extension V[G],which witnesses the failure of¬φ.The generic f i lter G usually collects information which approximates the desired statement.This process is in a sense similar to a f i eld extension.For instance,C would disagree with R on the statement∃x(x2=-1).One start with R and imposes a solution i of the polynomial x2+1=0 to get C=R[i].
The beginner is referred to[2]and[5]for an elementary introduction to forcing.More details can be found in the textbooks[3]and[6].Forcing is also related to boolean valued models,see[10]for instance.
The Cohen forcing adds reals to the universe.In set theory,reals are identif i ed with a countable binary sequence or countable sequence on ω.Cohen forcing approaches the generic Cohen real by f i nite strings.There are other forcings which adjoin dif f erent types of reals. For instance,Mathias forcing[7]is def i ned in Section 2.
The rest of this article is organised as follows:Section 2 introduces the Mathias forcing and its properties;Section 3 deals with a variation of Mathias forcing and focuses on the dif f erence with the usual Mathias forcing;Section 4 generalizes to uncountable space and proves the main theorem.
2 Mathias Forcing
Def i nition 1A pair(s,S)is called a Mathias pair,if
1.s is an strictly increasing function from some f i nite number n to ω.
2.S is an inf i nite subset of ω.
3.range(s)⊆min(S).
Def i nition 2Mathias forcing consists of all Mathias pairs with the partial order def i ned as:(s,S)≤(t,T)if s end extends t,range(s) ange(t)⊆T and S⊆T.
For a generic f i lter G,the Mathias real is def i ned as g=∪{t:∃T(t,T)∈G},which is an increasing function from ω to ω in the generic extension.
Def i nition 3A real g dominates a real f,if∃m∈ω∀n>m(f(n)<g(n)).
Def i nition 4 g∈ωω∩V[G]is dominating over V if∀f∈ωω∩V,g dominates f.
Def i nition 5 g∈ωω∩V[G]is unbounded by V if∀f∈ωω∩V,g is not dominated by f.
It is clear that a dominating real is unbounded.It can be proved that a Mathias real is dominating over the ground model,while a Cohen real is unbounded but not dominating.
3 Strengthen the Mathias Forcing
In this section,we consider a stronger version of the Mathias forcing.
Consider the strong Mathias forcing P0which consists of all Mathias pairs.(s,S)≤(t,T)if s end extends t,range(s) ange(t)⊆T,S⊆T and TS is f i nite.
Namely,we enhance the usual Mathias forcing with the last requirement.As with the Mathias forcing,we can def i ne the typical generic real g=∪{t:∃T(t,T)∈G}.
In contrast to Mathias forcing,the typical generic real of P0is not a dominating real. Theorem 6 g is not dominating over the ground model.
Proof A key observation is that,below any condition,there are exactlyℵ0many conditions.So this forcing is in a sense a disjoint union of c many Cohen forcings.

A contradiction.However,we still have the following.
Theorem 7 g is unbounded over the ground model.
Proof Suppose otherwise.Let(t,T)f dominate˙g.Moreover,by passing to a stronger condition,we can assume without loss of generality that
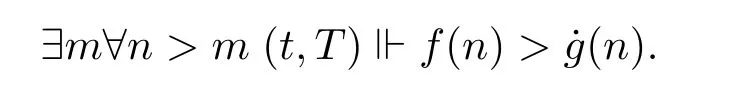
Now we let n=max{m+1,|t|}and extend(t,T)to(s,S)such that|s|>n and s(n)≥f(n). Since=s(n),we get a contradiction.
4 Generalization to Uncountable Space
In this section,we generalize the results to uncountable case.We will focus on the f i rst uncountable cardinal ω1.
An ω1-real is a function from ω1to ω1.
Def i nition 8 A pair(s,S)is called a ω1-Mathias pair,if
1.s is an strictly increasing function from some countable ordinal α to ω1.
2.S is an uncountable subset of ω1.
3.range(s)⊆min(S).
Def i nition 9Consider the strong ω1-Mathias forcing P1which consists of all ω1-Mathias pairs.(s,S)≤(t,T)if s end extends t,range(s) ange(t)⊆T,S⊆T and TS is countable.
Remark 10We might study the ω1-Mathias forcing.The generic ω1-real added by ω1-Mathias forcing is dominating.However,the question that whether reals were added is more complicated and we will not explain in this article.
Now we begin to study the properties of P1.
The main theorem we wish to prove is the following.
Theorem 11 The forcing P1adds no reals;the generic ω1-real is unbounded.If CH holds,then the generic ω1-real is not dominating.
Chain condition is usually a key to study a forcing.Set theoretic topologist usually prefer the forcing with countable chain condition(c.c.c.),as Martin’s Axiom can be applied there.However,we have the following lemma.
Lemma 12P1does not satisfy the countable chain condition.
Proof Fix a partition ω1=∪{Iα:α<ω1},with each Iαuncountable.Then the (∅,Iα)’s are mutually incompatible forcing notions.
The chain conditions plays an important role in preserving cardinal.Since the failure of c.c.c.,one would ask if ω1is preserved.
Fortunately,a closure property can be expected for P1.
Theorem 13P1is ω-closed.
Proof Let(s0,S0)≥(s1,S1)≥···≥(sn,Sn)≥···be a decreasing sequence of conditions.Def i ne s=∪{sn:n<ω}.Then s is an increasing function into ω1.Let domain(sn)=αn,domain(s)=α,then α=sup{αn:n∈ω}is a countable ordinal.
Let S=∩{Sn:n<ω}.Then S=S0∪{SnSn+1:n∈ω}.So S is uncountable.
Since for each n,range(sn)⊆min(Sn)≤min(S),range(s)⊆min(S).
Therefore,(s,S)is a condition.Since for each n,SnS=∪{SkSk+1:k≥n}is a countable set,(s,S)is a lower bound for the given decreasing sequence.
It is well known that ω-closed forcing does not add countable sequence of ordinals.In other words,it is ω-distributive.See[3],for instance.So ω1is preserved.Also,we have
Corollary 14P1does not add a real.
ω-closed forcing is proper,see[8].The class of forcing notions that are both ωdistributive and proper was studied in[9],which focus on the forcing axiom and preservation of a couple of combinatorial properties.An immediate consequence is the following.
Corollary 15Assume CH in the ground model,then in a generic extension by P1,or a countable support iteration of P1,all the following cardinal invariants are equal toℵ1

Remark 16This result is in contrast to the case of usual Mathias forcing.With a countable support iteration of the usual Mathias forcing,e,m,p,t,add(B),cov(B),add(L), cov(L)remainℵ1while the rest become c.
As before,if G is a generic f i lter of P,then let g=∪{t:∃T(t,T)∈G}.g is a generic ω1-real.
Unboundedness and dominating properties can be def i ned for a generic ω1-real,similar to Def i nitions 3 to 5.
Theorem 17g is an unbounded ω1-real over the ground model.
Proof The proof is similar to the proof of Theorem 7.
Theorem 18Assume CH holds in the ground model,then g is not dominating over the ground model.
In fact,we can prove a stronger theorem.
Theorem 19 Assume for any condition r in a forcing Q,{q∈Q:q≤r}has cardinalityℵ1.Then for any ω1-real h in the generic extension,there is in the ground model an ω1-real f,which is not dominated by h.
Proof The proof is similar to that of Theorem 6.Suppose the conclusion fails.Then there is some r∈Q such that˙h is a dominating ω1-real.
List{r′∈Q:r′≤r}={pα:α<ω1}.For each α,let qα≤pα,βα<ω1be such that qα˙h(α)=βα.Now def i ne in the ground model an ω1-real f with f(α)=βα.
Proof of Theorem 18 Assume CH holds in the ground model.Obviously,for any given condition(t,T)of P1,the cardinality of the set{(t′,T′)∈P1:(t′,T′)≤(t,T)}is
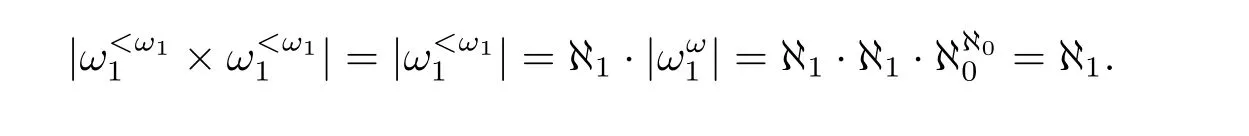
The second equality is due to the Hausdorf f’s formula;the last equality is CH.
Thus Theorem 19 applies and we conclude that the forcing P1adds an unbounded ω1-real but adds no dominating ω1-real.
Remark The results in this section can be generalize to any regular cardinal κ with κ<κ=κ.
[1]Cohen P J.The independence of the continuum hypothesis[J].Proc.Nat.Acad.Sci.,1963,50:1143-1148,
[2]Chow Timothy Y.A beginner’s guide to forcing[A].Communicating Mathematics,Vol.479 of Contemp.Math.[C].Providence RI:Amer.Math.Soc.,2009:25-40.
[3]Jech T.Set theory(3rd ed)[M].Amsterdamlin:Springer-Verlag,2003.
[4]Jech T.Multiple forcing[M].Vol.88 of Cambridge Tracts Math.,Cambridge:Cambridge Univ. Press,1986.
[5]Jech T.What is···forcing?[J].Notices Amer.Math.Soc.,2008,55(6):692-693.
[6]Kunen K.Set theory:an introduction to independence proofs[M].Vol.102 of Studies in Logic and the Foundations of Mathematics,Amsterdam:North-Holland Publishing Co.,1980.
[7]Mathias A.Happy families[J].Ann.Math.Logic.,1977,12(1):59-111.
[8]Shelah S.Proper forcing[M].Number 940 in Lecture Notes in Mathematics,Berlin:Springer-Verlag, 1982.
[9]Zhu Huiling.Distributive proper forcing axiom and cardinal invariants[J].Arch.Math.Logic,2013, 52(5-6):497-506,
[10]Luan Jingwen.Boolean valued model of polymerized axiom system[J].J.Math.,1997,17(2):64-70.
添加超实数而不加实数的力迫
朱慧灵,郑馥丹
(华南理工大学广州学院,广东广州510800)
本文研究了加强型Mathias力迫及其在不可数情形下的推广.通过力迫法,证明了Mathias力迫添加支配性实数,而加强型Mathias力迫添加的是无界、非支配性的实数.还证明了ω1上的Mathias型力迫添加的是无界、非支配性的ω1类实数且不添加新的实数.这些结论可应用于对实数上的基数不变量的研究.
ω1-超实数;Mathias力迫;支配性实数;无界实数;基数不变量
O144.3
A
0255-7797(2017)05-0911-05
∗Received date:2016-03-30Accepted date:2016-06-08
Supported by National Natural Science Foundation of China(11401567).
Biography:Zhu Huiling(1985-),male,born at Chenzhou,Hunan,Ph.D,associate professor, major in mathematical logic and set theory.
2010 MR Subject Classif i cation:03E17;03E35;03E50

