LIOUVILLE TYPE THEOREMS FOR A NONLINEAR ELLIPTIC EQUATION

XIANG Ni,CHEN Yong

(School of Mathematics and Statistics,Hubei University,Wuhan 430062,China)

LIOUVILLE TYPE THEOREMS FOR A NONLINEAR ELLIPTIC EQUATION

XIANG Ni,CHEN Yong

(School of Mathematics and Statistics,Hubei University,Wuhan 430062,China)

Let(Mn,g)be an n-dimensional complete noncompact Riemannian manifold.In this paper,we consider the Liouville type theorems for positive solutions to the following nonlinear elliptic equation：Δfu+aulogu=0,where a is a nonzero constant.By applying Bochner formula and the maximum principle,we obtain local gradient estimates of the Li-Yau type for positive solutions of the above equation on Riemannian manifolds with Bakry-Emery Ricci curvature bounded from below and some relevant Liouville type theorems,which improve some results of[7].

gradient estimate;nonlinear elliptic equation;Liouville-type theorem;maximum principle

1 Introduction

Let(Mn,g)be an n-dimensional complete Riemannian manifold.The drifting Laplacian is def i ned by Δf=Δ-∇f∇,where f is a smooth function on M.The N-Bakry-Emery Ricci tensor is def i ned by

for 0≤N＜∞and N=0 if and only if f=0,where f is some smooth function on M,∇2is the Hessian and Ric is the Ricci tensor.The∞-Bakry-Emery Ricci tensor is def i ned by

In particular,Ricf=λg is called a gradient Ricci soliton which is extensively studied in Ricci f l ow.

In this paper,we want to study positive solutions of the nonlinear elliptic equation with the drifting Laplacianon an n-dimensional complete Riemannian manifold(Mn,g),where a is a nonzero constant. When f=constant,the above equation(1.1)reduces to

Equation(1.2)is closely related to Ricci soliton[9]and the famous Gross Logarithmic Sobolev inequality[6].Ma[9]f i rst studied the positive solutions of equation(1.2)and derived a local gradient estimate for the case a＜0.Then the gradient estimate for the case a＞0 is obtained in[4]and[15]by studying the related heat equation of(1.2).More progress of this and related equations can be found in[2,8,10,13,14]and the references therein.Recently, inspired by the method used by Brighton in[1],Huang and Ma[7]derived local gradient estimates of the Li-Yau type for positive solutions of equations(1.2).These estimates are dif f erent from those in[4,9,15].Using these estimate,they can easily get some Liouville type theorems.We want to generalize their results to equation(1.1)and we obtain the following results

Theorem 1.1Let(Mn,g)be an n-dimensional complete Riemannian manifold with≥-K,where K is a nonnegative constant.Assuming that u is a positive solution of the nonlinear elliptic eq.(1.1).Then on Bp(R),we have the following inequalities

(1)If a＞0,then

Let R→∞,we have the following gradient estimates on complete noncompact Riemannian manifolds.

Corollary 1.2Let(Mn,g)be an n-dimensional complete noncompact Riemannian manifold with-K,where K is a nonnegative constant.Assuming that u is a positive solution of the nonlinear elliptic eq.(1.1).Then the following inequalities hold

(1)if a＞0,then

In particular,for a＜0,if a≤-K,then max{0,a+K}=0.Thus,(1.5)implies |∇u|≤0 whenever u is a bounded positive solution of the nonlinear elliptic(1.1).Hence u≡1.Therefore the following Liouville-type result follows.

Corollary 1.3Let(Mn,g)be an n-dimensional complete noncompact Riemannian manifold with RicNf≥-K,where K is a nonnegative constant.Assuming that u is a bounded positive solution of(1.1)with a＜0.If a≤-K,then u≡1.

In particular,we have the following conclusion

Corollary 1.4Let(Mn,g)be an n-dimensional complete noncompact Riemannian manifold with RicNf≥0.Assuming that u is a bounded positive solution def i ned of(1.1) with a＜0,then u≡1.

The above results are obtained under the assumption that RicNfis bounded by below. We can also obtain similar results under the assumption that Ricfis bounded by below.

Theorem 1.5Let(Mn,g)be an n-dimensional complete Riemannian manifold with Ricf(BP(2R))≥-(n-1)H,and|∇f|≤K,where K and H is a nonnegative constant. Assuming that u is a positive solution of the nonlinear elliptic eq.(1.1)on Bp(2R).Then on Bp(R),the following inequalities hold

(1)if a＞0,then

In particular,for a＜0,if a≤-(n-1)H,then max{0,a+(n-1)H}=0.Thus,(1.10) implies|∇u|≤0 whenever u is a bounded positive solution to(1.1).Hence,that u≡1. Therefore,the following Liouville-type result follows

Corollary 1.7Let(Mn,g)be an n-dimensional complete noncompact Riemannian manifold with Ricf≥-(n-1)H,and|∇f|≤K,where K and H is a nonnegative constant. Assuming that u is a bounded positive solution of(1.1)with a＜0.If a≤-(n-1)H,then u≡1.

In particular,we have the following conclusion.

Corollary 1.8Let(Mn,g)be an n-dimensional complete noncompact Riemannian manifold with Ricf≥0.Assuming that u is a bounded positive solution of(1.1)with a＜0, then u≡1.

2 The Proof of Theorems

Now we are in the position to give the proof of Theorem 1.1.First we recall the following key lemma.

Lemma 2.1 Let(Mn,g)be an n-dimensional complete Riemannian manifold with RicNf(BP(2R))≥-K,where K is a nonnegative constant.Assuming that u is a positive solution to nonlinear elliptic eq.(1.1)on Bp(2R).Then on Bp(R),the following inequalities hold

(1)If a＞0,then

Proof of Lemma 2.1 Let h=uϵ,where ϵ 6=0 is a constant to determined.Then we have

A simple calculation implies

Therefore we get

In order to obtain the bound of|∇h|by applying the maximum principle to(2.7),it is sufficient to choose the coefficienis positive,that is

Now we begin to prove Theorem 1.1 which will follow by applying comparison theorems and Bochner formula to an appropriate function h.

Proof of Theorem 1.1 We f i rst prove the case of a＞0.Let m be a cut-of ffunction such that m(r)=1 for r≤1,m(r)=0 for r≥2,0≤m(r)≤1,and

for positive constants c1and c2.Denote by ρ(x)=d(x,p)the distance between x and p in (Mn,g).Let

Making use of an argument of Calabi[3](see also Cheng and Yau[5]),we can assume without loss of generality that the function φ is smooth in Bp(2R).Then we have

It was shown by Qian[11]that

Hence we have

It follows that

Def i ne G=φ|∇h|2,we will use the maximum principle for G on Bp(2R).Assume G achieves its maximum at the point x0∈Bp(2R)and assume G(x0)＞0(otherwise this is obvious).Then at the point x0,it holds that

Using(2.1)in Lemma 2.1,we obtain

where the second inequality used(2.10).Multiplying both sides of(2.14)by,we obtain

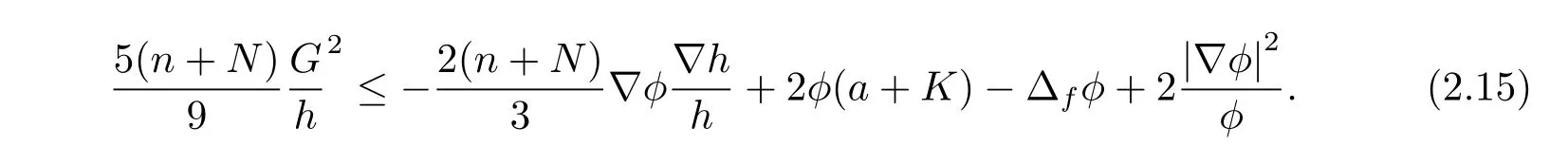
Then using the Cauchy inequality,we have

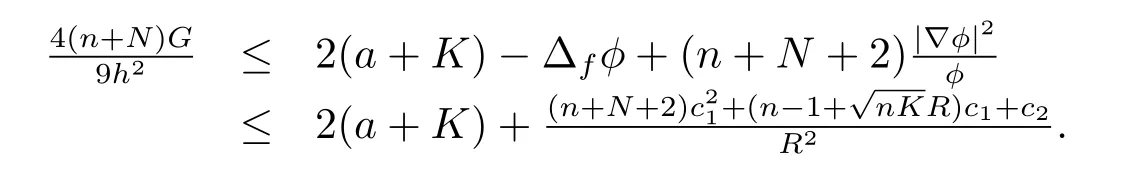
So for x0∈Bp(R),we have

This shows

and

This concludes the proof of inequality(1.4)of Theorm 1.1.

Now we are in the position to give a brief proof of Theorem 1.5.

Skept of the Proof of Theorem 1.5 Noticing that we have the following Bochner formula to h with Ricf,

Moreover,the comparison theorem holds true in the following form(see Theorem 1.1 in [12])：if Ricf≥-K and|∇f|≤K,we have

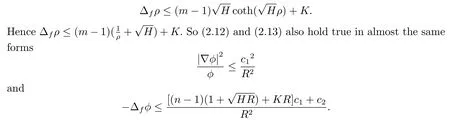
Noticing the above facts,the proof of Theorem 1.5 is the same to that of Theorem 1.1,so we omit it here.

[1]Brighton K.A Liouville-type theorem for smooth metric measure spaces[J].Geom.Anal.,2010, 23(2)：562-570.

[2]Cao X,Ljungberg B F,Liu B.Dif f erential Harnack estimates for a nonlinear heat equation[J].Funct. Anal.,2013,265(10)：2312-2330.

[3]Calabi E.An extension of E.Hopf’s maximum principle with a pplication to Riemannian geometry [J].Duke Math.,1958,25(1)：45-56.

[4]Chen L,Chen W.Gradient estimates for a nonlinear parabolic equation on complete noncompact Riemannian manifolds[J].Ann.Glob.,Anal.Geom.,2009,35(4)：397-404.

[5]Cheng S,Yau S.Dif f erential equations on Riemannian manifolds and their geometric applications[J]. Communn.Pure.,Appl.Math.,1975,28(3)：333-354.

[6]Gross L.Logarithmic Sobolev inequality and contractivity properties of semigroups[J].Berlin：Springer,1993,61(2)：318-322.

[7]Huang G,Ma B.Gradient estimates and Liouville type theorems for a nonlinear elliptic equation[J] Arch.Math.,2015,105(5)：491-499.

[8]Huang G,Huang Z,Li H.Gradient estimates and dif f erential Hararck inequalities for a nonlinear parabolic equation on Riemannian manifolds[J].Ann.Glob.,Anal.Geom.,2013,43(3)：209-232

[9]Ma L.Gradient estimates for a simple elliptic equation on complete noncompact Riemannian manifolds[J].Funct.Anal.,2006,241(1)：374-382.

[10]Qian B.A uniform bound for the solutions to a simple nonlinear equation on Riemannian manifolds[J].Nonlinear Anal,2010,73(6)：1538-1542.

[11]Qian Z.A comparison theorem for an elliptic operator[J].Potent.Anal.,1998,8(2)：137-142.

[12]Wei G,Wylie W.Comparison geomtry for the Bakry-Emery Ricci tensor[J].Dif f.Geom.,2009, 83(2)：377-405.

[13]Wu J Y.Li-Yau type estimates for a nonlinear parabolic equation on complete manifolds[J].Math. Anal.,2010,369(1)：400-407.

[14]Yau S T.Harmonic functions on complete Riemannian manifolds[J].Comm.Pure.,Anal.Math., 1975,28(2)：201-228.

[15]Yang Y.Gradient estimates for a nonlinear parabolic equation on Riemannian manifolds[J].Proc. Amer.,Math.Soc.,2008,136(11)：4095-4102.

一类非线性椭圆方程的刘维尔型定理

向妮,陈勇

(湖北大学数学与统计学院,湖北武汉430062)

设(Mn,g)是一个n维非紧的完备黎曼流行.本文考虑有正解的非线性椭圆方程Δfu+ aulogu=0的刘维尔型定理,其中a是一个非零常数.利用Bochner公式和极大值原理,获得了以上方程在Bakry-Emery里奇曲率有下界时正解的Li-Yau型梯度估计和某些有关的刘维尔理论,推广了文献[7]的结果.

梯度估计;非线性椭圆方程;刘维尔型定理;极大值原理

O175.25;O175.29

A

0255-7797(2017)05-0977-10

∗Received date：2016-04-29Accepted date：2016-08-24

Supported by the National Natural Science Foundation of China(11201131); Hubei Key Laboratory of Applied Mathematics(Hubei University).

Biography：Xiang Ni(1981-),female,born at Chongqing,associate professor,major in fully nonlinear partial dif f erential equations.

2010 MR Subject Classif i cation：53C21;35J60