奇异高阶积分边值问题正解的全局结构
沈文国
(兰州工业学院基础学科部,甘肃兰州730050)
奇异高阶积分边值问题正解的全局结构
沈文国
(兰州工业学院基础学科部,甘肃兰州730050)
本文研究了带Riemann-Stieltjes积分边值条件的奇异高阶积分边值问题正解的全局分歧结构.利用相关文献,获得了此类问题的格林函数并推证其满足的性质,同时可获得此类问题等价于一个全连续算子方程;其次,在满足所给的条件时,利用Krein-Rutmann定理建立了此类问题对应的线性问题存在简单的主特征值;最后,当非线性项在零和无穷远处满足非渐进线性增长条件、参数满足不同范围的值时,利用Dancer全局分歧定理、Zeidler全局分歧定理和序列集取极限的方法,建立了此类问题正解的全局结构,进而获得了正解的存在性,推广了文献[8]中的主要结果.
奇异高阶积分边值问题;全局分岐;正解
1 引言
利用锥上不动点理论,文献[1-6]研究了边值问题正解的存在性;文献[7-8]研究了带Riemann-Stieltjes积分边值条件的高阶问题,其中2012年,当ra(t)f(x)=λf(t,x)时,文献[8]研究了下列奇异高阶问题

其中f(t,x)在t=0,t=1处奇异,α,β:[0,1]→ℜ分别是有界变差函数.
应用分歧方法,文献[9-11]研究了二阶边值问题;文献[12-14]研究了四阶边值问题;文献[15]研究了高维问题;文献[16-17]研究了带Riemann-Stieltjes积分边值条件问题.
受上述文献的启发,本文研究奇异高阶含Riemann-Stieltjes积分边值条件的问题(1.1)正解的存在性问题.本文做如下假设

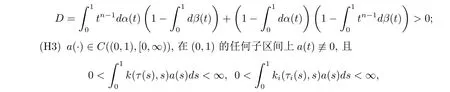
k(τ(s),s),ki(τi(s),s)分别由引理2.2与引理2.3给出;
(H4)f(·)∈C([0,∞),[0,∞)),对任何s>0,都有f(s)>0成立; (H5)f0,f∞∈(0,+∞);
(H6)f0∈(0,+∞)且f∞=∞; (H7)f0=0且f∞=∞; (H8)f0=∞且f∞=∞,
其中
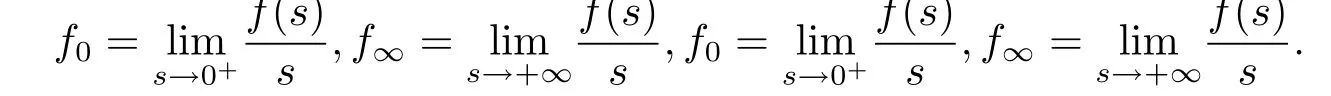
本章安排如下:在第二部分给出格林函数及其性质;第三部分给出预备知识;第四部分给出问题(1.1)至少存在一个正解的主要定理及证明.
2 格林函数及其性质

引理2.1(见文献[8,引理1])假设条件(H1)和(H2)成立.对于任何y∈C[0,1],则问题(2.1)存在唯一解

其中
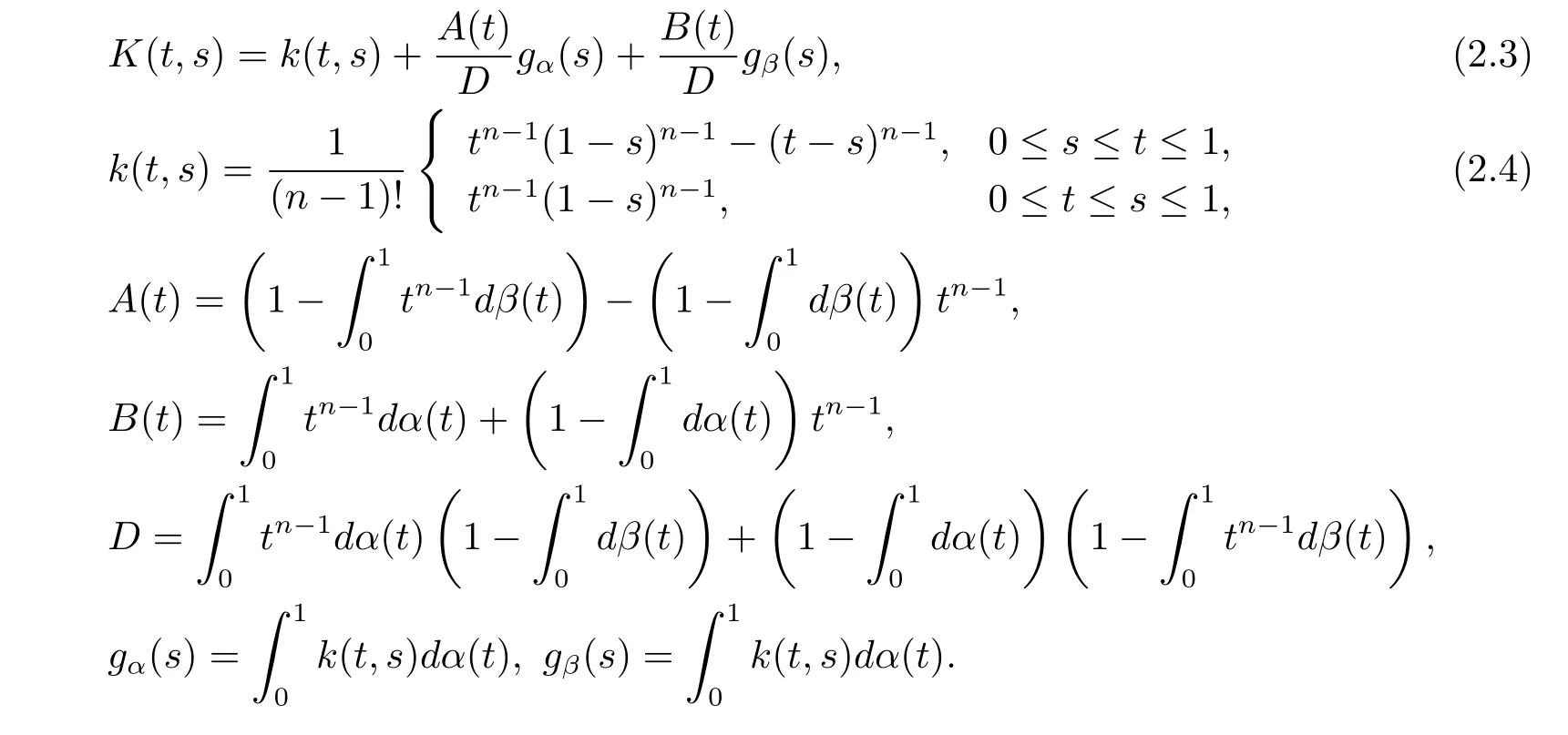
引理2.2(见文献[8,引理2])由(2.4)式定义的k(t,s)满足下列性质

其中

引理2.3 k(t,s)由(2.4)式定义,i=2,···,n,下式成立

并且ki(t,s)满足
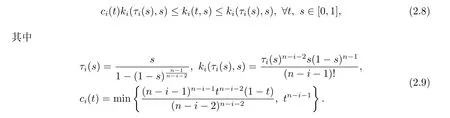
证相似于文献[7]第1937-1938页中定理3.1的证明方法,易得引理2.3,故证明略.
引理2.4(见文献[8,引理3])假设条件(H1)和(H2)成立.由(2.3)式定义的K(t,s)满足下列性质
(i)K(t,s)在[0,1]×[0,1]上连续且K(t,s)≥0;
(ii)对于任意t,s∈[0,1]都有K(t,s)≤K(s)成立,对于任意t,s∈[0,1],下式成立
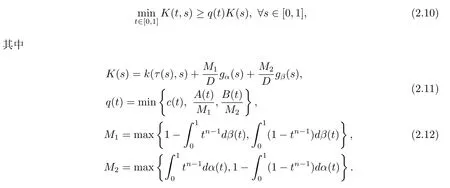
引理2.5(见文献[8,引理4])假设条件(H1)和(H2)成立.则对于y∈C[0,1]且y≥0, (2.1)式的唯一解满足
其中q(t)由引理2.3(ii)给出.
3 预备知识

容易验证L为闭算子且L-1:Y→D(L)是全连续算子.
令Σ为(1.1)在[0,∞)×E上正解集合的闭包.
定义锥
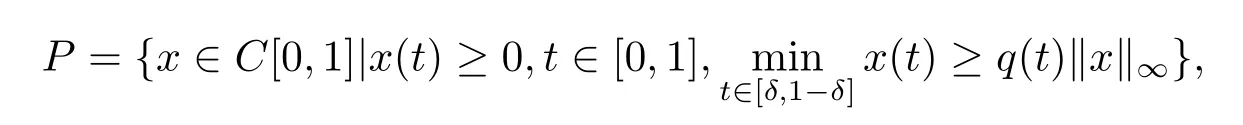
其中q(t)由引理2.3(ii)给出,且对于r>0,令Ωr={x∈P|kxkE<r}.首先考虑线性问题
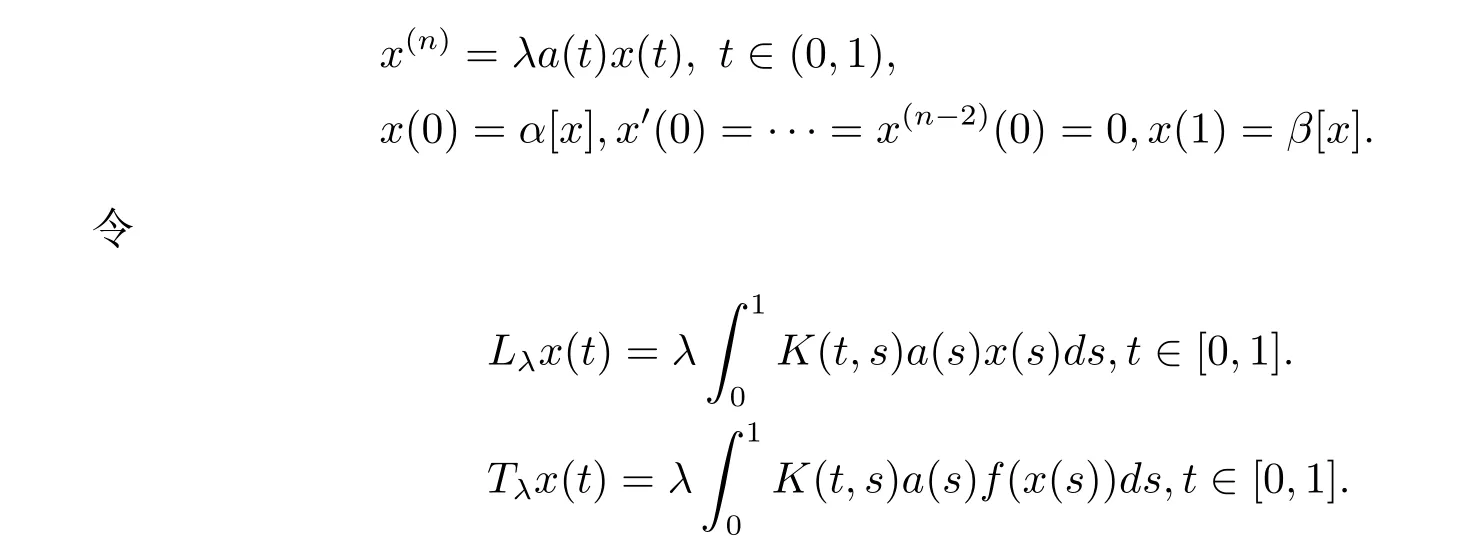
由Krein-Rutmann定理(见文献[18,定理2.5],亦可参考文献[19]或[20]),可得下列引理.
引理3.1设(H1)-(H3)成立,r(Lλ)是Lλ的谱半径.则r(Lλ)6=0且Lλ有一个对应于第一特征值的正的特征函数φ1∈intP,它是简单的并且再没有别的特征值对应正的特征函数.
引理3.2设(H1)-(H4)成立,则问题(1.1)的解x(t)满足
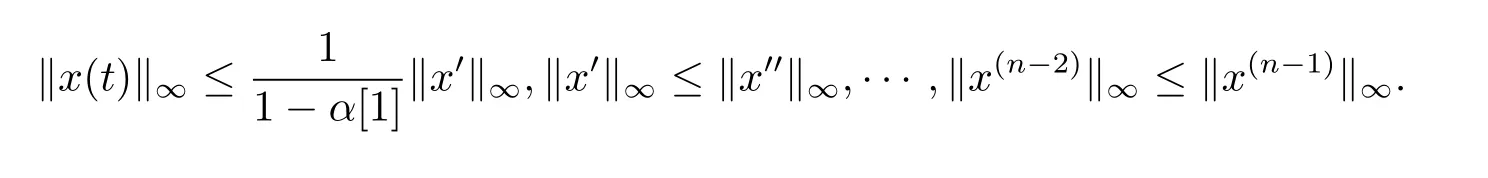

结论获证.
引理3.3设(H1)-(H4)成立.假设{(µk,xk)}⊂(0,∞)×P是问题(1.1)的一个正解序列,存在常数c0>0,使得kµkk≤c0,且

由(H3)可得

结合引理3.2,存在常数M2>0满足kxk(t)kE≤M2.与已知条件矛盾,结论获证.
引理3.4(见文献[17])设X是一个Banach空间且令{Cn|n=1,2,···}是X中的闭连通分支序列.假设
(i)存在zn∈Cn,n=1,2,···和z∗∈X,使得zn→z∗;
(ii)rn=sup{kxk|x∈Cn}=∞;
和xni∈Cni,使得xni→x}(见文献[21]).
4 主要结果
首先考虑下列特征值问题

事实上,对所有(t,s)∈[0,1]×[0,1],由引理2.1-2.3可得

其中

则对于任意t,s∈[0,1],i=1,···,n,都有

其中

由(4.4)式,i=1,···,n,可得

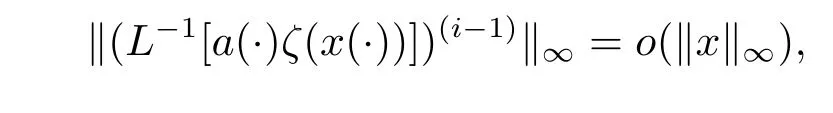
由L-1的紧性结合(H3),i=1,···,n,可得进而i=1,···,n,k(L-1[a(·)ζ(x(·))])(i-1)k∞=o(kxkE).即(4.3)式得证.
由引理3.1和全局分岐定理(可参考Dancer[22]和Zeidler[23]推论15.12),对于问题(4.2),可得如下结论.
引理4.1令(H1)-(H5)成立,(rλ
f10,0)是问题(4.2)的一个分岐点.进而,存‡在式正解的一个连通分支C,满足C(⊂[0,∞)×E),并且C在[0,∞)×P中连接和
注4.1问题(4.1)的形如(1,x)的任何解将产生问题(1.1)的一个解x.为了获得结论,仅仅证明C在[0,∞)×P中穿过超平面{1}×E即可.
下面是本文主要结果.
定理4.1令(H1)-(H5)成立.要么λ1/f∞<r<λ1/f0成立,要么λ1/f0<r<λ1/f∞成立.则问题(1.1)至少有一个正解.
证由引理4.1易得结论,故证明略.
定理4.2令(H1)-(H4)和(H6)成立.假设r∈(0,λf01).则问题(1.1)至少有一个正解.
证受文献[24]的启发,可以定义截断函数f如下


[1]Jiang Heping,Jiang Wei.The existence of a positive solution for nonlinear fractional functional dif f erential equations[J].J.Math.,2011,31(3):440-446.
[2]郝兆才,孔盟.一类奇异泛函微分方程边值问题的多重正解[J].数学杂志,2013,33(1):75-82.
[3]Ji Yuede,Guo Yanoing.The existence of countably many positive solutions for some nonlinear nth order m-point boundary value problems[J].J.Comput.Appl.Math.,2009,232(2):187-200.
[4]Yang Jinbao,Wei Zhongli.Positive solutions of nth order m-point boundary value problem[J].Appl. Math.Comput.,2008,202(2):715-720.
[5]Pang Changci,Wei Dong,Wei Zhongli.Green’s function and positive solutions of nth order m-point boundary value problem[J].Appl.Math.Comput.,2006,182:1231-1239.
[6]Graef J R,Yang Bo.positive solutions to a multi-point or nonlinear higher order boundary value problem[J].J.Math.Anal.Appl.,2006,316(2):409-421.
[7]Webb J R L.Nonlocal conjugate type boundary value problem of higher order[J].Nonl.Anal.,2009, 71(5-6):1933-1940.
[8]Shen Wenguo.Positive solutions to semipositone higher order singular nonlocal boundary value problems[J].J.Lanzhou Univ.(Nat.Sci.),2012,48(2):97-100.
[9]Dai Guowei,Ma Ruyun.Unilateral global bifurcation phenomena and nodal solutions for p-Laplacian[J].J.Dif f.Equ.,2012,252:2448-2468.
[10]Dai Guowei.Bifurcation and nodal solutions for p-Laplacian problems with non-asymptotic nonlinearity at 0 or∞[J].Appl.Math.Lett.,2013,26:46-50.
[11]Dai Guowei,Ma Ruyun.Unilateral global bifurcation for p-Laplacian with non-p-1-linearization nonlinearity[J].Disc.Contin.Dyn.Syst.,2015,35(1):99-116.
[12]Rynne B P.Inf i nitely many solutions of superlinear fourth order boundary value problems[J].Topol. Meth.Nonl.Anal.,2002,19(2):303-312.
[13]Shen Wenguo.Global structure of nodal solutions for a fourth-order two-point boundary value problem[J].Appl.Math.Comput.,2012,219(1):88-98.
[14]Ma Ruyun.Nodal solutions for a fourth-order two-order boundary value problem[J].J.Math.Anal. Appl.,2006,314(1):254-265.
[15]Shi Junping,Wang Yuwen.On global bifurcation for quasilinear elliptic systems on bounded domains[J].J.Dif f.Equ.,2009,246:2788-2812.
[16]Shen Wenguo,He Tao.Global structure of positive solutions for a singular fourth-order integral boundary value problem[J].Disc.Dyn.Nat.Soc.Vol.2014,Article ID 614376,7 pages.
[17]Ma Ruyun,An Yulian.Global structure of itive solutions for nonlocal boundary value problems involving integral conditions[J].Nonl.Anal.,2009,71(1):4364-4376.
[18]Krasnosel’ii M A.Positive solutions of operator equations[M].The Netherlands:P.Noordhof fLtd., 1964.
[19]Zhang G,Sun J.Positive solutions of m-point boundary value problems[J].J.Math.Anal.Appl., 2004,291:406-418.
[20]Guo D,Sun J.Nonlinear integral equations[M].Ji’nan:Shandong Sci.Tech.Press,1987(in Chinese).
[21]Whyburn G T.Topological analysis[M].Princeton:Princeton University Press,1958.
[22]Dancer E.Global solutions branches for positive maps[J].Arch.Rat.Mech.Anal.,1974,55:207-213.
[23]Zeidler E.Nonlinear functional analysis and its applications[A].Translated from the German by Peter R Wadsack.Fixed point theorems[C].New York:Springer-Verlag,1986.
[24]Ambrosetti A,Calahorrano R M,Dobarro F R.Global branching for discontinuous problems[J]. Comment.Math.Univ.Carolin.,1990,31:213-222.
GLOBAL BIFURCATION OF POSITIVE SOLUTIONS FOR SINGULAR HIGH-ORDER PROBLEMS INVOLVING STIELTJES INTEGRAL CONDITIONS
SHEN Wen-guo
(Department of Basic Courses,Lanzhou Institute of Technology,Lanzhou 730050,China)
In this paper,we establish global bifurcation structure of positive solutions for a class of singular higher-order boundary value problems.First,according to the relevant literature,we obtain that the Green fuction and its property for the above problem.Meanwhile, we can obtain that the above problem is equivalent to the completely continuous operator equation.Second,we have that the above linear problem exists simple principal eigenvalue by the Krein-Rutman theorem.Finally,we establish the global bifurcation structure of positive solutions with non-asymptotic nonlinearity at or by Dancer and Zeidler global bifurcation theorems and the approximation of connected components which extends and improves the corresponding results of Shen[8].
high-order singular boundary problems;global bifurcation;positive solutions
O175.8
A
0255-7797(2017)05-1054-11
2016-01-04接收日期:2016-04-22
国家自然科学基金(11561038);甘肃省自然科学基金(145RJZA087)
沈文国(1963-),男,甘肃景泰,教授,主要研究方向:分歧理论及非线性微分方程.
2010 MR Subject Classif i cation:34B15;34K18
- 数学杂志的其它文章
- 具有相依理赔量的离散时间风险模型的破产问题
- COMPLETE CONVERGENCE FOR ARRAYS OF ROWWISE M-NSD RANDOM VARIABLES
- OSCILLATION OF NONLINEAR IMPULSIVE DELAY HYPERBOLIC EQUATION WITH FUNCTIONAL ARGUMENTS VIA RICCATI METHOD
- 偏微分方程边值反问题的数值方法研究
- A CLASS OF PROJECTIVELY FLAT SPHERICALLY SYMMETRIC FINSLER METRICS
- ESTIMATION OF GROWTH OF MEROMORPHIC SOLUTIONS OF SECOND ORDER ALGEBRAIC DIFFERENTIAL EQUATIONS

