活性粉末混凝土T形梁正截面承载力试验研究

姚 杰, 高 日, 景向阳

(1.蒙冀铁路有限公司，内蒙古呼和浩特 010000; 2.北京交通大学土木建筑工程学院，北京100044)

活性粉末混凝土T形梁正截面承载力试验研究

姚 杰1, 高 日2, 景向阳1

(1.蒙冀铁路有限公司，内蒙古呼和浩特 010000; 2.北京交通大学土木建筑工程学院，北京100044)

文章通过无筋和配筋活性粉末混凝土T形梁的抗弯试验，对活性粉末混凝土梁的弯曲性能及其影响因素进行分析，与普通钢筋混凝土相比，活性粉末混凝土的抗裂性能和极限承载力有了显著的提高，参照普通钢筋混凝土梁正截面承载力计算模型，建立了钢筋活性粉末混凝土受弯构件正截面承载力计算公式。

活性粉末； 混凝土； 抗弯性能； 承载力

活性粉末混凝土(Reactive Powder Concrete简称RPC) 具有高强度、高韧性和高耐久性的特点，在工程领域具有广泛的应用前景[1-2]。RPC强度很高，因此构件截面尺寸相对较小，得以减轻自重，增大结构跨度，降低造价。

Graybeal研究了普通钢筋UHPC梁抗弯性能，同时还研究了足尺寸UHPC预应力梁的变形性能[3]。文献[4-6] 通过HRB400钢筋RPC梁受弯试验，研究了RPC受弯构件受力机理，建立了考虑截面受拉区RPC 拉应力贡献的正截面承载力、刚度及裂缝宽度计算公式，总结出RPC矩形配筋梁正截面抗裂计算方法及正截面承载力的计算方法。本文研究了无筋和配筋活性粉末混凝土T形梁的受弯全过程，在此基础上根据普通混凝土的理论分析方法建立了承载力计算方法。

1 试验概况

1.1 试验材料

RPC试验的主要材料：拉法基42.5#普通硅酸盐水泥；硅灰比表面积为14.31 mm2/g；石英砂：粒径范围为0～1.25 mm；高性能减水剂：新型非萘系高性能减水剂，减水率29 %，含固量为31 %；新型DJ-1型高性能矿物外加剂；钢纤维：特制细圆形表面镀铜钢纤维，直径为0.22 mm，长度为12～15 mm。RPC试验配合比见表1。

表1 RPC试验配合比 kg/m3

1.2 试件设计

试验设计了2个无筋RPC梁、2个HRB400的RPC梁。试验梁截面尺寸见图1，长2 200 mm，基本参数见表2。

表2 试验梁的设计参数

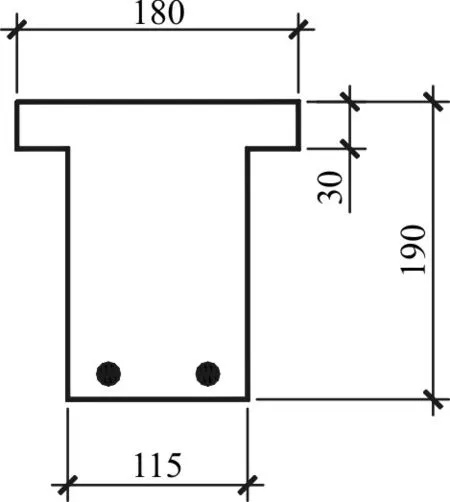
图1 RPC试验梁横截面

1.3 测点布置

试验主要研究RPC梁的抗弯性能，在纯弯段内沿梁高和梁底纵向布置电阻应变片以测得截面的中性轴位置和梁的开裂；位移测点布置在RPC梁的跨中和加载点位置。

1.4 试验加载

试验梁采用两点集中加载。采用液压千斤顶进行分级加载，量测仪器包括静态应变采集仪、应变式位移传感器。

2 试验现象与结果

2.1 RPC无筋梁受弯全过程

2.1.1 无筋梁受弯过程的三个阶段

无筋梁试验的荷载-挠度曲线见图2。受弯过程可以分为三个阶段：

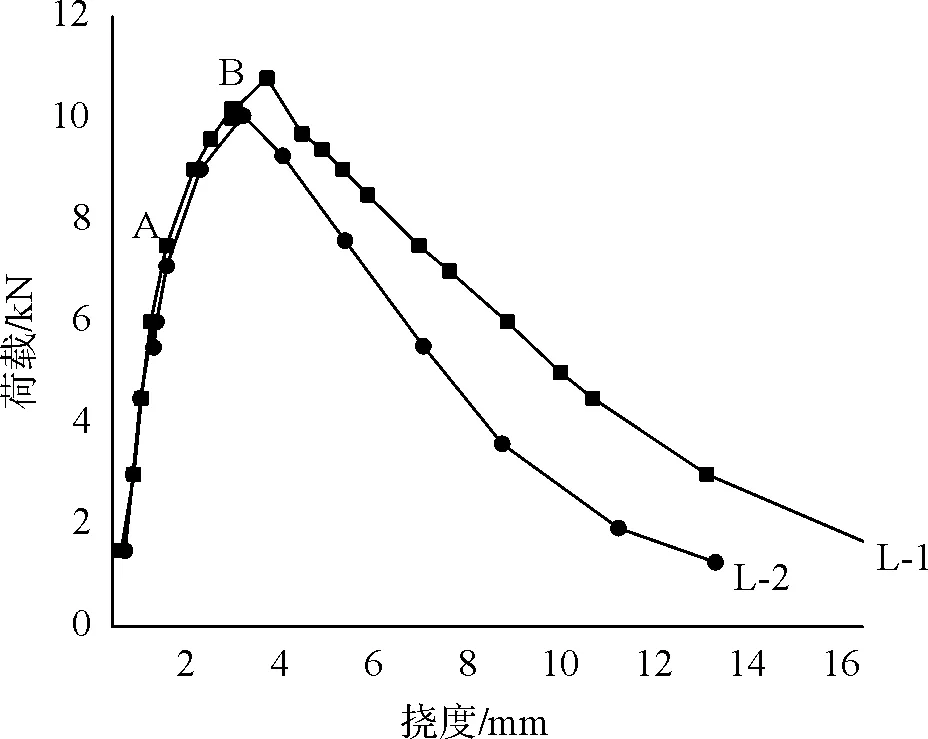
图2 RPC无筋受弯构件弯矩挠度曲线

(1)弹性阶段。加载初期，受拉区与受压区的应力分布沿截面高度分布基本是线性关系，荷载-挠度曲线是直线。

(2)裂缝开展阶段。过A点后，基体内部微裂缝扩展为宏观裂缝，由于裂缝出现，拉应变增大，中性轴高度不断增加，受拉区应力分布出现非线性，且拉应变增长速率比压应变大，受拉区曲线逐渐变曲。

(3)破坏阶段。过B点后，钢纤维与基体间界面粘结强度达到极限，纤维不断拔出，中性轴继续上移，受拉区应力合力作用力臂的减小速率大于其合力的增加速率，跨中挠度增长很快，梁断裂破坏。

2.1.2 梁的抗弯性对比

与普通素混凝土梁抗弯性能对比，RPC无筋梁的抗弯性能具有以下特点。

(1)RPC的抗弯能力比普通混凝土高很多，同样条件下RPC的初裂荷载比后者的极限荷载还要高。

(2)受弯构件初裂后，而RPC的抗弯承载力在裂后仍有较大提高，一般其极限弯矩可达初裂弯矩的1.5倍左右。

(3)弯曲破坏时受拉区钢纤维是从基体中被拔出而不是被拉断，破坏呈现出一定的延性特征。

2.2 RPC配筋梁受弯全过程

RPC梁抗弯试验得到RPC适筋梁荷载-挠度曲线如图3所示。RPC配筋梁的受力变形全过程可分为三个阶段：

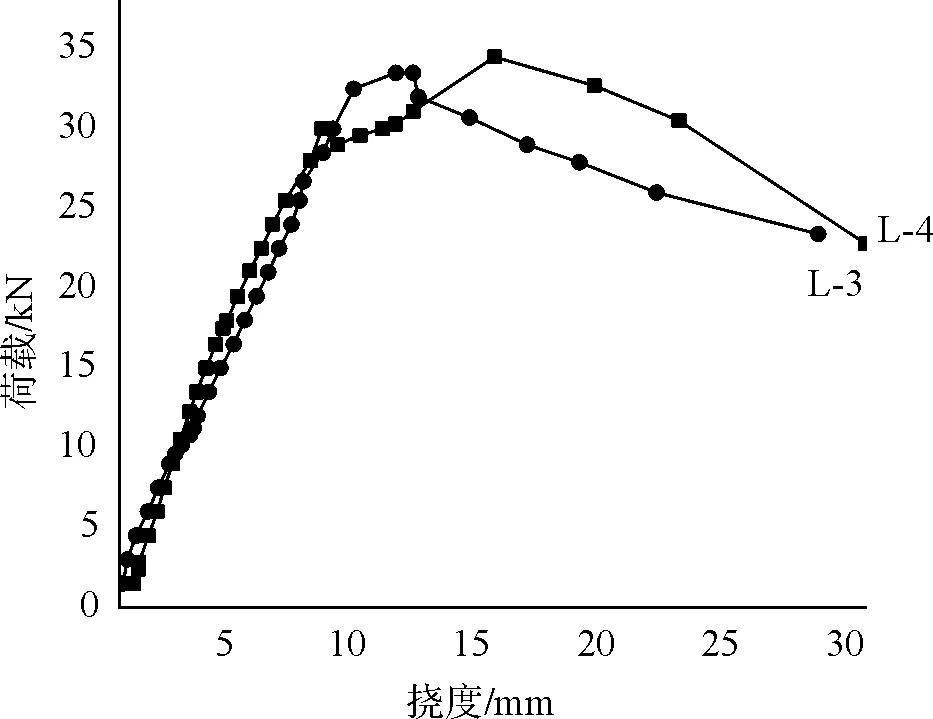
图3 钢筋 RPC梁荷载-挠度曲线

(1)弹性阶段。梁在承受较小荷载时，构件基本处于弹性状态，RPC的拉、压应力均随高度线性变化，呈三角形分布。

(2)裂缝扩展阶段。荷载增加，裂缝增宽并不断向上扩展，由RPC承担的拉力逐渐转移给钢筋和钢纤维共同承担，钢纤维的阻裂作用使裂缝向上发展变得缓慢，使梁的整体刚度明显提高，荷载-挠度曲线弯曲不明显。

(3)破坏阶段。荷载继续增加，裂缝数量增多、宽度增大并向受压区边缘延伸；当纵筋屈服，裂缝条数增加很少，裂缝宽度增大，向上延伸加快，荷载-挠度曲线再次出现拐点，荷载增大较慢而梁的挠度增加很快；继续加载，RPC 裂缝扩展明显，受压区RPC被压坏，梁破坏。

3 RPC受弯构件正截面承载力计算

RPC配筋梁正截面考虑RPC受拉区的抗拉作用。

3.1 一般假设规定

(1)平截面假定成立。RPC材料剔除粗骨料，优化颗粒级配，比普通混凝土提高了匀质性。试验结果表明RPC配筋梁符合平截面假定。

(2) 纵筋与RPC材料之间无滑移。

(3)RPC的轴压及轴拉应力-应变近似关系：

当0<εrc<εrco时σrc=Ercεrc

(1)

当εrco≤εrc≤εrcu时σrc=frc

(2)

其中：σrc和εrc为RPC压应力和对应的压应变；frc和εrco为RPC的抗压强度和对应的压应变；εrcu为RPC受压区极限压应变。根据国内外试验资料可知，RPC材料的极限压应变约为普通混凝土的2～3倍[3]，故本文建议取εrcu=0.0075。

RPC受压应力-应变计算曲线见图4。

图4 RPC受压应力-应变计算曲线

3.2 RPC配筋梁正截面极限承载力的计算

3.2.1 RPC梁正截面受压区应力等效

抗弯承载力的理论计算较为繁杂，承载力计算通常根据受压区合力作用位置和合力大小不变的原则，将实际应力分布等效成矩形应力图，便于设计计算。可采用受压区平均应力系数k1、压区应力合力作用位置到受压边缘的距离系数k2(简称受压区形心系数)来表征RPC配筋梁达到极限强度时受压区的应力分布情况(图5)。

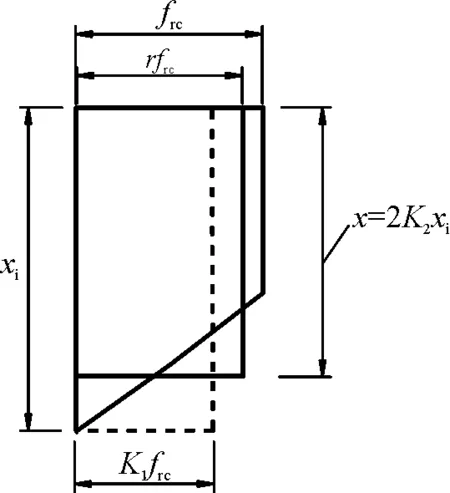
图5 受压区RPC的应力简化分布

构件达到极限强度时，k1、k2的计算公式为：

(3)

(4)

等效矩形应力图的高度x为：

x=2k2xi

(5)

令β=2k1，则β为矩形应力图高度x与中性轴高度xi的比值，即有：

(6)

图5中γ为等效矩形应力系数。由两应力图块合力大小相等的原则，经整理可得：

(7)

(8)

一般认为弯压与轴压极限压应变的比在1.5～1.8[8]之间，此结论也可以近似应用于RPC，故可近似取φ=0.5～0.7，可得β=0.778～0.713，γ=0.964～0.912。《对于RPC的β和γ取值，考虑混凝土及钢纤维混凝土的取值和文献[7]得出的结论，本文近似取：

(9)

从而，RPC配筋梁的弯曲抗压强度为：

(10)

frcm是采用等效矩形压应力图后的折算强度指标，RPC配筋梁承载力极限状态时的截面等效受压区高度则为：

x=0.7xi

(11)

3.2.2 受拉区应力图形的等效

考虑RPC中钢纤维的抗拉作用，等效矩形拉应力图形的高度xt可参考钢纤维混凝土的取法[8]，取为中性轴以下截面的高度，如图6(d)所示，即有：

(12)

3.2.3 钢筋RPC梁正截面承载力的计算

RPC配筋梁正截面承载力简化计算模型见图6。

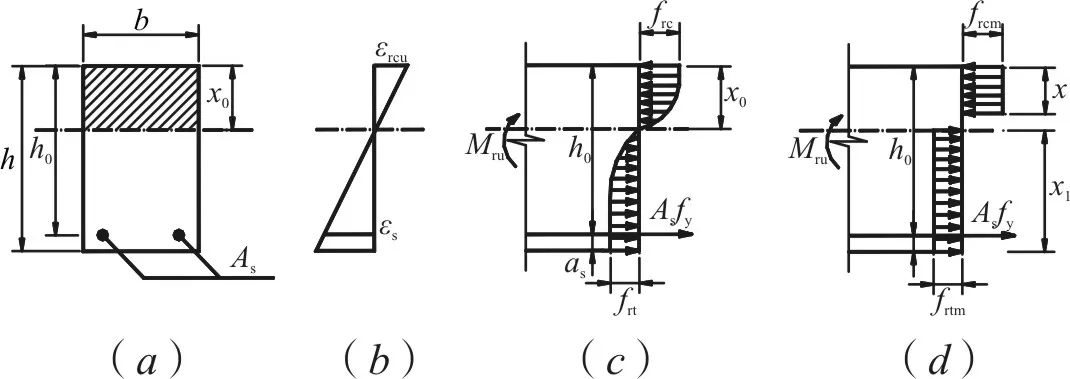
图6 RPC配筋梁正截面承载力简化计算模型

由截面内力平衡可得极限承载力基本方程：

∑N=0frcmbx=fyAs+frtmbxt

(13)

对受拉区钢筋合力作用点取矩得：

(14)

若对受压区合力作用点取矩得：

(15)

式中，as为纵向受拉钢筋合力作用点至截面受拉区边缘的距离。

frtm可通过RPC配筋梁的弯曲破坏试验，利用式(14)、(15)计算得到：

(16)

为了便于进行试验统计计算，可将截面受拉区高度xt近似取为h0-x可得：

(17)

将试验梁的实测极限弯矩及有关数据代入上式，即可求出相应的frtm、βtm为钢纤维对PRC拉区抗拉性能的影响系数，由于本次试验梁的数据较少，现根据本次试验和文献[9]中的数据分析知道βtm在1.6～1.9之间，由于试验数据有限无法进行统计分析，保守起见建议可近似取βtm=1.5。

根据上述结论并结合RPC梁的试验数据求出适筋梁L-3和L-4的极限弯矩理论值为21.92 kN·m，梁的极限弯矩实测平均值为22.84 kN·m，由此可见由简化计算模型建立的RPC配筋梁正截面承载力计算公式与试验结果吻合很好。

4 结论

本文通过无筋和配筋RPC梁的受力变形全过程，对其弯曲性能及破坏特征进行了系统分析，得出以下主要结论：

(1)RPC无筋梁开裂后承载能力还会进一步提高，极限弯矩可达初裂弯矩的1.5倍左右。RPC无筋梁呈现出良好的延性特征。

(2)RPC配筋梁从加载至破坏整个过程中，钢纤维对RPC配筋梁的裂缝控制作用明显，与同条件钢筋混凝土梁相比裂缝出现较晚，梁的整体刚度得到提高。

(3)钢纤维的存在，RPC正截面的受力分析考虑受拉区RPC的抗拉作用；弯曲抗拉强度frtm采用钢纤维混凝土的计算模式，钢纤维对钢纤维混凝土梁拉区抗拉性能的影响系数在试验分析的基础之上保守起见取为1.5。

[1] 徐海宾，邓宗才. UHPC梁开裂弯矩和裂缝试验[J].哈尔滨工业大学学报，2014，46(4)：87-92.

[2] 邓宗才，王义超，肖锐. 高强钢筋 UHPC 梁抗弯性能试验研究与理论分析[J]. 应用基础与工程科学学报，2015，23(1)：68-78.

[3] GRAYBEAL B. Characterization of the behavior of ultra-high performance concrete[D]. Maryland: University of Maryland，2005.

[4] 王兆宁.活性粉末混凝土矩形截面配筋梁抗弯性能研究[D]. 北京：北京交通大学，2005.

[5] 郑文忠，李莉.钢筋活性粉末混凝土简支梁正截面受力性能试验研究[J].建筑结构学报，2011，32(6) : 125-134.

[6] 于涛涛.钢筋活性粉末混凝土受弯构件正截面承载力的研究[D]. 北京：北京交通大学，2011.

[7] 高丹盈．钢纤维混凝土及其配筋构件力学性能的研究[D].大连：大连理工大学，1989.

[8] 高丹盈，刘建秀．钢纤维混凝土基本理论[M]．北京：科学技术文献出版社，1994.

[9] 陈广智，孟世强，阎培渝. 养护条件和配合比对活性粉末混土变形率的影响[J].工业建筑，2003，33(9):63-65.

[10] 曹霞，常婧，王艳俊. 高强钢筋RPC 梁受弯构件正截面承载力试验研究[J]. 河南理工大学学报：自然科学版，2015，34(1)：109-115.

姚杰(1973～)，男，研究生，高级工程师。

TU317+. 1

A

[定稿日期]2017-06-12