路基挡墙黏性土主动土压力计算误差分析——以某二级公路挡墙为例

吴 锐，胡定波

（1.浙江省交通规划设计研究院,浙江 杭州 310006;2.台州市黄岩区交通运输局,浙江 台州 318020）

路基挡墙黏性土主动土压力计算误差分析
——以某二级公路挡墙为例

吴 锐1，胡定波2

（1.浙江省交通规划设计研究院,浙江 杭州 310006;2.台州市黄岩区交通运输局,浙江 台州 318020）

对某二级公路路肩式挡墙墙背黏性土主动土压力采用了常见的两种方法计算，即经典库伦理论的等效内摩擦角法和力多变形法。计算结果表明，这两种方法计算出来的该挡墙的抗滑动稳定系数误差达到33.4%，并且，随着墙高的增加，误差增加很快。因此，在设计高墙时，应酌情降低D，在计算黏性土的主动土压力时，最好是按照实际测定的c、值，采用力的数解法计算。

路基挡墙；黏性土；主动土压力计算；抗滑动稳定系数

0 引言

考虑到工程的经济性和就地取材的原则，公路挡土墙墙后的填土不可能采用远运砂性土，而是就近取土填筑，不可避免地造成填土或多或少具有一定的黏聚力。我国现行路基规范规定采用库伦理论计算路基挡墙所受到的主动土压力。经典库伦理论只考虑不具有黏聚力的砂性土的土压力问题。当墙背填料为黏性土时，土的黏聚力对主动土压力的影响很大，因此应该考虑黏聚力的影响。

以库伦理论为基础的计算黏性土主动土压力的方法主要有等效内摩擦角法和力多边形法。等效内摩擦角法是指按照抗剪强度相等或土压力相等的原则，把黏性土的黏聚力的影响考虑到内摩擦角这一参数中，然后按砂性土的公式来计算主动土压力。然而，由于影响土压力数值的因素是多方面的，包括墙高、墙型、墙后填土表面荷载情况等。按照实际测定的C、φ值，采用力的多边形法来计算黏性土的主动土压力，是更符合实际的做法。本文以某二级公路的路肩式挡墙为例，即挡墙边界条件相对简单的情况下，在满足现行规范对于重力式挡墙各项计算要求的前提下，分析等效内摩擦角法计算的主动土压力作用下，挡墙墙身沿基底抗滑移稳定系数的误差。

1 工程概况

某丘陵区二级公路，设计速度80 km/h，路基全宽12 m。路基土由含碎石亚黏土（黏性土）、含黏性土碎石等组成。厚度变化较大，一般小于4 m，个别地段可达6～8 m。一般无软弱夹层，下伏坡残积层和各类基层（风化层），属正常路段，地基土具一定强度，可直接作公路路基基础。地形起伏而决定路基形式以挖方和填方相间交替。考虑到压缩用地和支档防护要求，局部路段采用仰斜式路肩挡墙。墙背填土重度γ=18 kN/m3，c=5 kPa，=25°。墙背摩擦角δ=2/3。地基容许承载力[σ]=250 kPa，基底摩擦系数f=0.4。墙身材料为砌体，重度为20 kN/m3，砌体容许压应力[σ]=500 kPa。挡墙断面如图1所示。

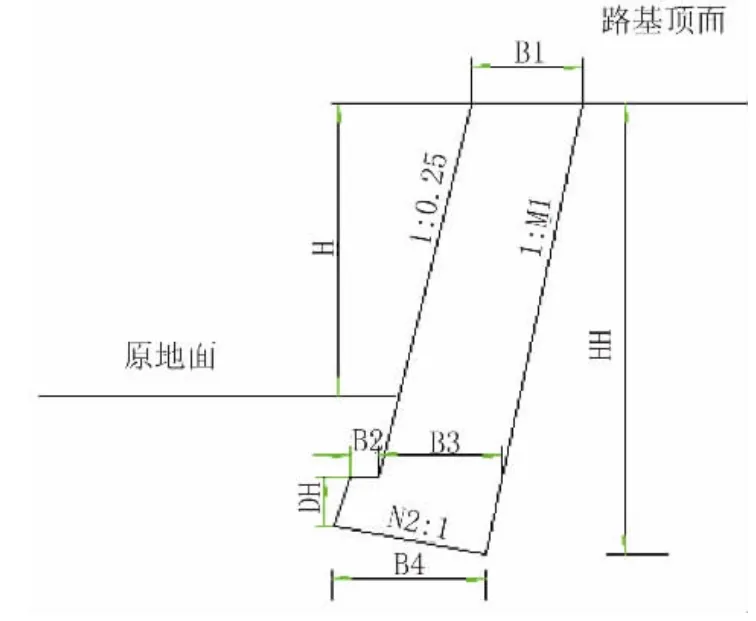
图1 路肩式挡墙断面图

以5 m高的挡墙为例，参照公路设计手册路基分册[1]，墙身拟定的各部位尺寸及参数为：N1= 0.25，B1=B2=1.2 m，B3=0.3，DH=0.5 m。

2 等效内摩擦角法和力多变形法计算黏性土的主动土压力

2.1 等效内摩擦角法

图2为等效内摩擦角法计算主动土压力示意图。

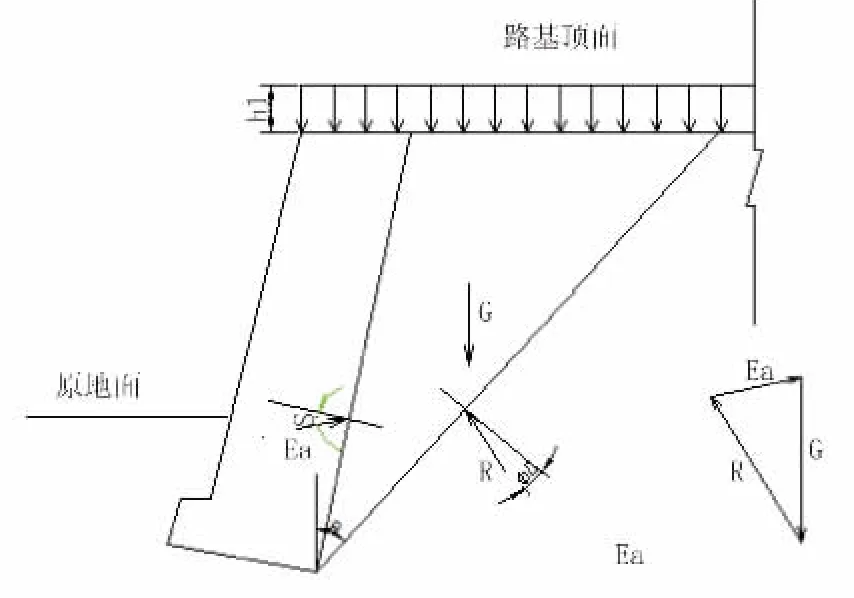
图2 等效内摩擦角法计算土压力示意图

2.1.1 等效内摩擦角计算

2.1.2 荷载当量土柱高度计算

根据规范，车辆荷载作用在挡土墙墙后填土引起的附加土侧压力，可以按照下式换算成等代均布土层厚度计算：

式中：γ为土的容重；q为车辆附加荷载标准值（kN/m2），按照墙高 5 m根据规范内插得到q=16.25 kN/m2，故 h0=16.25/18=0.9 m。

2.1.3 土压力计算

假设破裂面交于荷载内部。根据路肩式挡墙破裂面交于内部的破裂角θ计算公式,可得tanθ= 0.865 8,故θ=40°53′06″。破裂面位置符合假设。继而根据路肩挡墙破裂面交于荷载内部的主动土压力计算公式，可得主动土压力Ea=72.61 kN。其水平分量EX和竖直分量Ey计算如下：

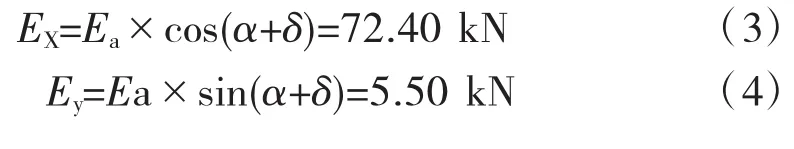
2.2 力多边形法

图3为力多边形法计算主动土压力示意图。

图3 力多边形法计算土压力示意图

2.2.1 裂缝区深度计算

裂缝区实际深hc'=hc-h0=-0.03 m

2.2.2 土压力计算

假设破裂面交于荷载内部。根据路肩式挡墙破裂面交于内部的破裂角θ计算公式可得tanθ= 0.877 9，故θ=40°16′45″。破裂面位置符合假设。继而根据路肩挡墙破裂面交于荷载内部的主动土压力计算公式，可得：

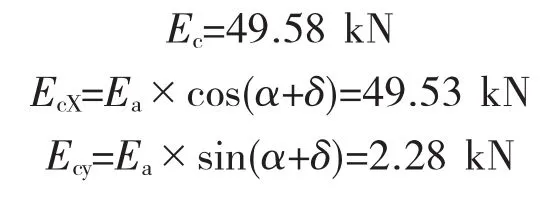
3 抗滑动稳定系数计算及分析

上述挡墙设计在通过规范要求的设计状态基本验算，进行挡墙抗滑稳定、抗倾覆稳定和整体稳定性验算的前提下，分析两种不同的主动土压力计算方法对抗滑稳定系数的影响。采用公式K= [N+Ex×tanα]×f/(Ex-N tanα)分别计算挡墙的滑动稳定系数，结果为：采用等效内摩擦角法和力多变形法的抗滑稳定系数分别为1.44和2.16，误差达到33.4%。改变墙身高度，按照《公路设计手册——路基》[1]拟定墙身的各部位尺寸，挡墙高度分别为3 m、4 m、6 m和7 m。分别采用等效内摩擦角法和力多边形法计算主动土压力前提下的挡墙抗滑稳定系数，结果见表1。

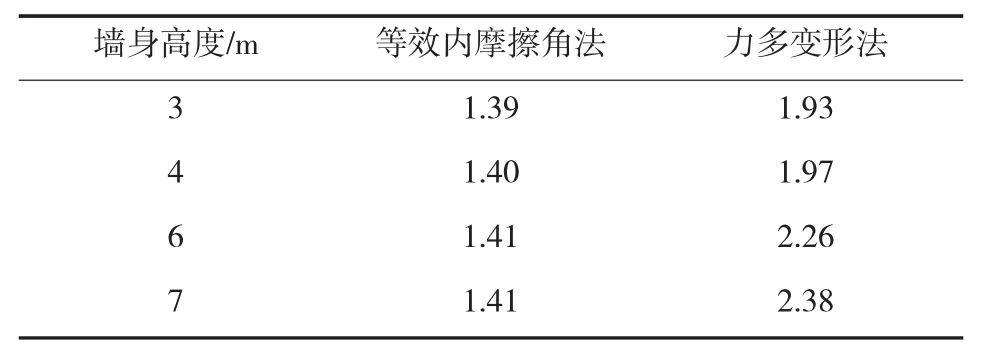
表1 等效内摩擦角法和力多边形法计算的抗滑稳定系数

可以看出，随着墙高的增加，误差增加很快。因此，在设计高墙时，应酌情降低D；在计算黏性土的主动土压力时，最好是按照实际测定的c、值，采用力的数解法计算。

4 结语

极限平衡理论是从破裂棱体的静力平衡条件出发，假定墙身及破裂棱体为刚体。这与实际情况并不相符，特别是在墙背倾角较大的情况下。更重要的是，由于没有考虑土的应力-应变关系，没有考虑墙身、基底及填土的共同作用，因而只能求得极限平衡时的压力而得不到位移。实际上，墙身位移对土压力影响非常明显。用有限元法对挡土墙进行数值分析是解决这个问题的途径，同时需要用模型试验或现场实测资料来验证，有待进一步实践探讨。

[1]交通部第二公路勘察设计院.公路设计手册——路基[M].北京：人民交通出版社，2001.

[2]JTG D30—2015，公路路基设计规范[S].

U416.1

B

1009-7716（2017）09-0196-02

10.16799/j.cnki.csdqyfh.2017.09.059

2017-07-07

吴锐（1977-），男，四川广安人，高级工程师，从事路线互通设计工作。