基于贝叶斯学习的动态投资组合选择

郭文英

(首都经济贸易大学统计学院，北京 1000070)

基于贝叶斯学习的动态投资组合选择

郭文英

(首都经济贸易大学统计学院，北京 1000070)

假设金融市场中有两种风险资产，并且每种资产的收益中均含有不可观测项、对应的风险既有系统性风险又有自身特有风险，具有幂效用函数的投资者运用贝叶斯学习方法最优地选取自己的动态投资组合。理论模型与数值分析显示，在一定的投资期限内，对风险资产的投入是风险厌恶程度的减函数；但超过某一时刻，则相反。当风险厌恶程度不变时，对不可观测因素的了解使得长、短期的投资策略不同。而且这个转折点随投资者的风险厌恶程度的增加而减小。风险资产与不可观测因素的相关性与风险的大小成反比例关系。

贝叶斯学习；HJB方程；动态投资

1 引言

投资组合选择问题是金融理论与实务的基本问题。Markowitz提出经典的均值方差投资组合选择模型，随后许多的学者分析了离散或连续时间投资，在理论、实证分析等方面极大地丰富了投资组合选择。Kolm[1]对此作了综述。

在金融市场中，随着时间的变化和金融数据的增加，投资者不断地更新所获得的信息，并将新信息应用到自己的投资组合选择中。现有理论中，贝叶斯学习过程是一种能够较好地描述投资者的这种调整过程的方法。考虑连续时间投资：Xia Yihong[2]假设股票的收益是某可观测变量的线性函数，其中的斜率遵循O—U过程，投资者通过对斜率的学习构建投资组合；袁子甲等[3]假设金融市场只有一种风险资产，具有CRRA型效用函数的投资者运用贝叶斯学习不断更新资产的收益，然后运用鞅方法给出最优投资组合策略。考虑离散时间投资：Brandt等[4]讨论了当风险资产的收益是可预测时，对收益中不确定参数应用贝叶斯学习，从而导致了对风险资产需求的减少；杨朝军等[5]实证分析了中国证券市场数据，在已知资产收益率的历史数据和预测变量的条件下，运用贝叶斯学习分析了参数不确定性对投资组合的影响。陈志英[6]假设市场状态之间的转换符合马尔科夫机制，投资者运用贝叶斯学习准则更新他们对当前市场状态的判断，建立了状态变化和投资者学习行为下资产组合选择模型。考虑单期投资，Ando[7]运用贝叶斯理论估计经典的均值方差模型中的不确定性参数的值，得到改进的多期均值方差模型并用实际金融数据和蒙特卡罗模拟给出数值分析；Virbickaite等[8]运用非参数贝叶斯学习估计投资组合收益的分布，通过最小化单期收益的方差得到最优投资策略；Zhu Shushang等[9]讨论了基于贝叶斯概率的均值CVaR模型。本文也利用贝叶斯过程分析投资者的学习行为。

以上以及大量的文献认为超额收益是可预测到的[10-12]。然而在学术界，关于影响收益的所有因素是否均可以被预测到这个话题仍存在不同看法[13-14])。Brennan[15]认为金融决策模型最为一般性的设定应该是投资策略集依赖于一系列不可观测的状态变量。但是，鲜有文献讨论存在不可观测因素的动态投资组合选择。Nicole等[16]分析市场中只有一种风险资产，假设收益受可观测到的与不可观测到的随时间变化的因素的共同影响，投资者能够从已实现的收益中利用贝叶斯学习来了解这两种因素，最后给出了此时的投资策略，并作了数值分析。本文在此基础上，假设市场中有两种风险资产，并且收益受不可观测因素的影响，同时每种风险资产都有系统风险与自身特有风险时，然后运用贝叶斯学习过程分析投资者的最优动态投资策略，并作数值分析。

2 基本模型

假设投资期为[0,T]，金融市场有一种无风险资产、两种风险资产，其中风险资产的收益不仅与已知参数有关，而且与不可观测到的变量有关，风险资产不仅有系统性风险，而且还有自身的特有风险。因此，在t时刻无风险资产的价格S0(t)、风险资产的价格Si(t)满足:

dyi(t)=kyi(μyi-yi(t))dt+σyi(t)dWi(t)

其中r(t)为无风险利率，θi(t)为预期收益率，假设θi(t)>0，yi(t)为不可观测到的变量。Z(t)为市场因素，Wi(t)为第i种风险资产特有的因素，并且Z(t)与Wi(t)均为标准Brown运动、且相互独立。

因此风险资产的超额收益θi(t)+ai(t)yi(t)就是已知参数与不可观测到的变量的代数和。不可观测到变量yi(t)的存在说明，已知参数(或可预测变量)不可能解释超额收益的所有可能变化，它是已知参数的良好补充。如果ai(t)=0，则不存在不可观测到的变量；如果ai(t)≠0，投资者不能够观测到预期超额收益，但他可以通过观测已实现的收益，对不可观测的收益运用贝叶斯学习。根据Liptser 等[17]，这个贝叶斯学习过程满足：

(1)

(2)

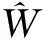
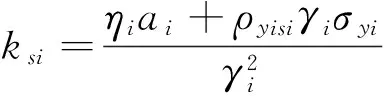
其中ρyisi是风险资产与不可观测变量的相关系数，ksi与ρyisi密切相关。

在投资组合中，记对第i种风险资产的投资比例为xi(t)，i=1,2。则对无风险资产的投资就是1-x1(t)-x2(t)。

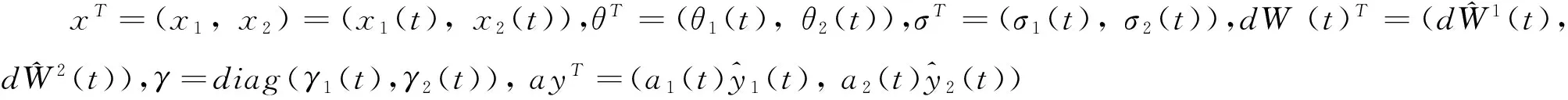
假设交易是连续的，且无交易费用，在任意时刻对无风险资产没有借贷限制、对风险资产可以买空。设初始财富为R(0)=R，则投资组合的收益R(t)满足：

(3)

3 最优投资策略

投资的目的是通过选取一定的投资策略在T时刻基于最终财富RT的预期效用达到最优。假设投资者的效用函数为风险厌恶程度为λ>1的幂函数。因此对应的优化模型为：

(4)

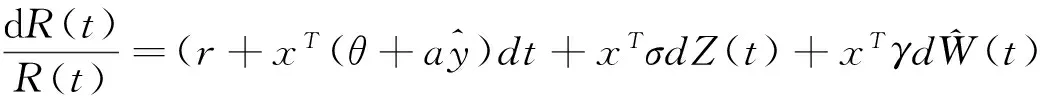
模型(4)是一个标准的随机优化问题。投资组合的收益R(t)由x控制，因此x是t、R(t)的函数式。根据优化理论，模型(4)的价值函数为：

J(R,t)是目前给定信息集Ft上基于最终财富的效用函数的条件预期。设J(R,t)关于t、R(t)、y是二次连续可导的。因此运用动态规划理论，模型(4)的HJB方程为：

(5)

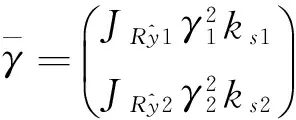
定理1：基于贝叶斯学习的动态投资组合的最优策略为：

(6)

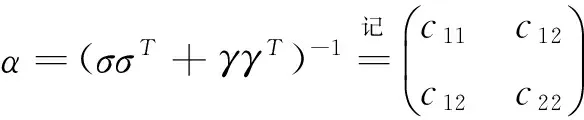
证明：由(5)式可得到。

定理2：基于贝叶斯学习的动态投资组合的价值函数为：

(7)

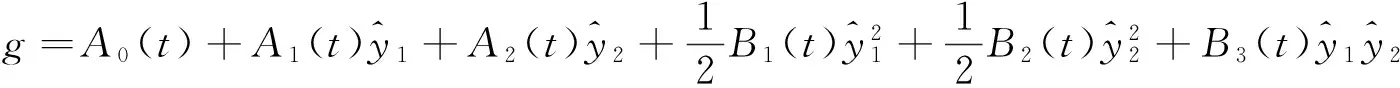
证明：将(6)代入(5)式有：

(8)

由价值函数的表达式(7)有：

将上述表达式代入(8)式，可以得到：

(9)

(10)

(11)

(12)

(13)

(14)

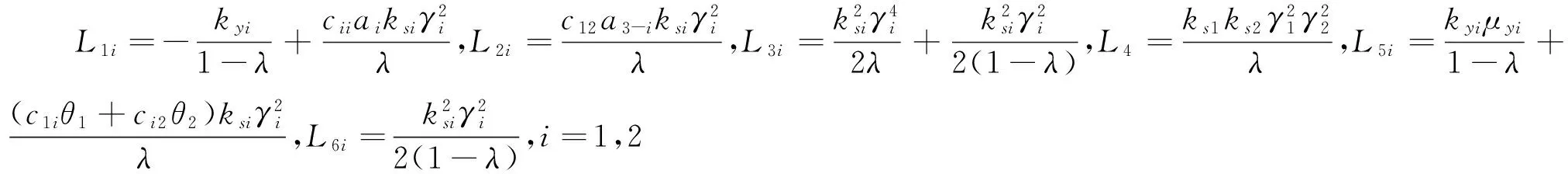
求解微分方程组(9)——(14)式，可以得到价值函数中的系数A0(t),A1(t),A2(t),B1(t),B2(t),B3(t)的解。从而得到(7)式的表达式。

对于以上(9)——(14)式微分方程组，无法求出它们的解析解，但可以求得数值解。有了数值解后，同样可以分析投资者对风险资产的投入比例。

由定理2，将JR,JRR的表达式代入(6)，可以得到所对应的最优策略为：

(15)

可以看到，最优投资策略依赖于风险厌恶程度与风险资产的波动大小，并且由两部分构成，第一部分只与已知参数的预期超额收益有关；第二项与贝叶斯学习有关。

4 数值分析

为了更清楚地看到贝叶斯学习对投资组合选择的影响，本文借鉴文献[16]的原始数据，给出数值分析。为了突出显示模型(4)的结论，同时也为了计算简单，本文假设所需参数均为常数。

表1 数值分析中参数的值

在表1所给参数下，利用Matlab2012b可以得到微分方程组(9)——(14)式的数值解，图1——6给出λ=4时的价值函数(7)中的系数A0(t),A1(t),A2(t),B1(t),B2(t),B3(t)解。

图1 λ=4时A0的解

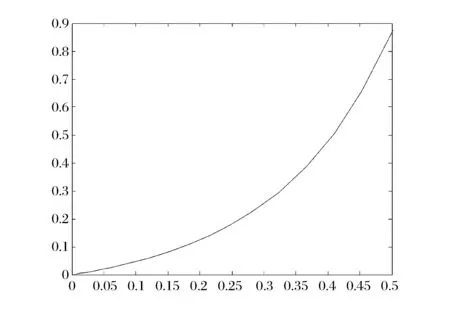
图2 λ=4时A1的解

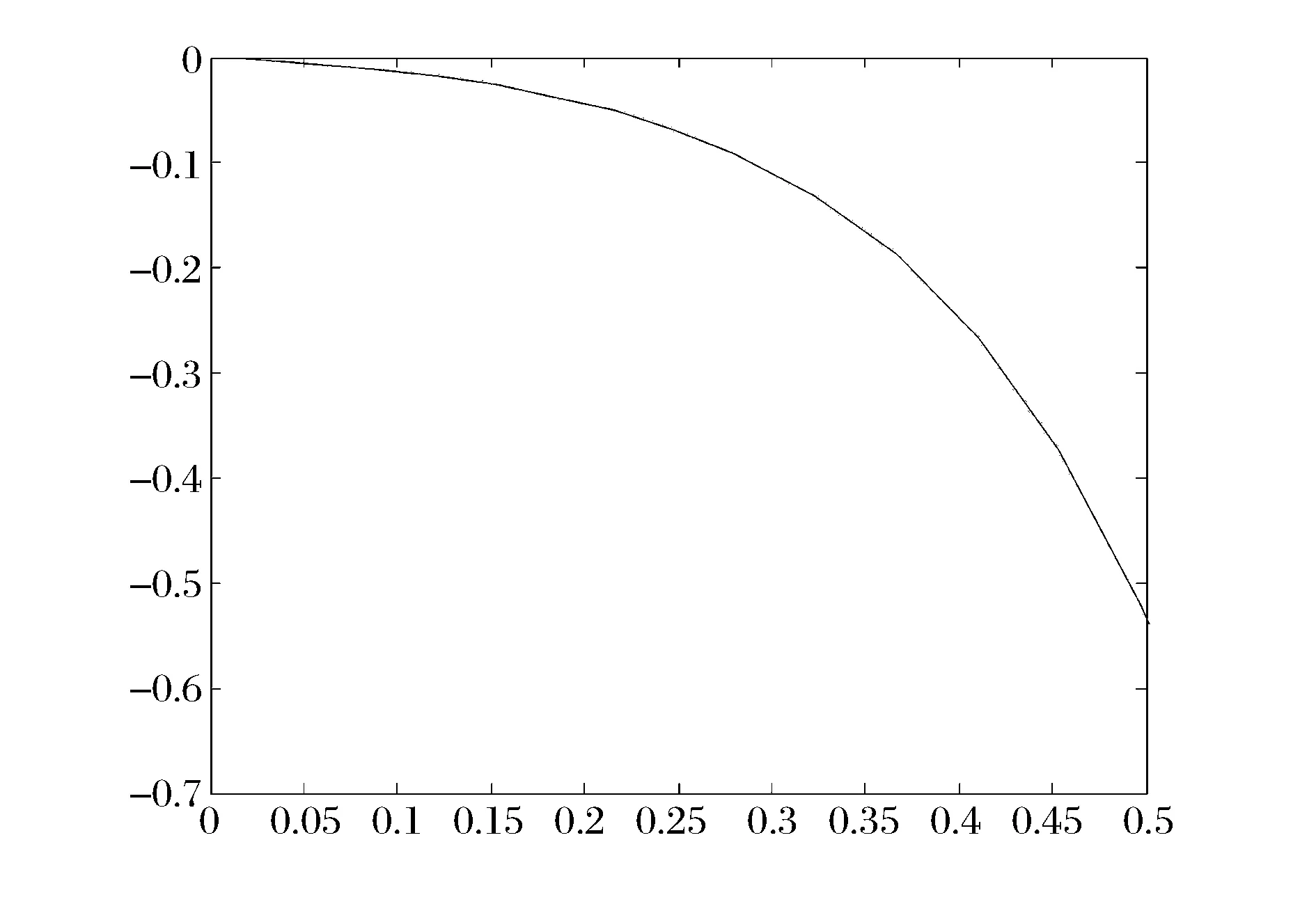
图3 λ=4时A2的解

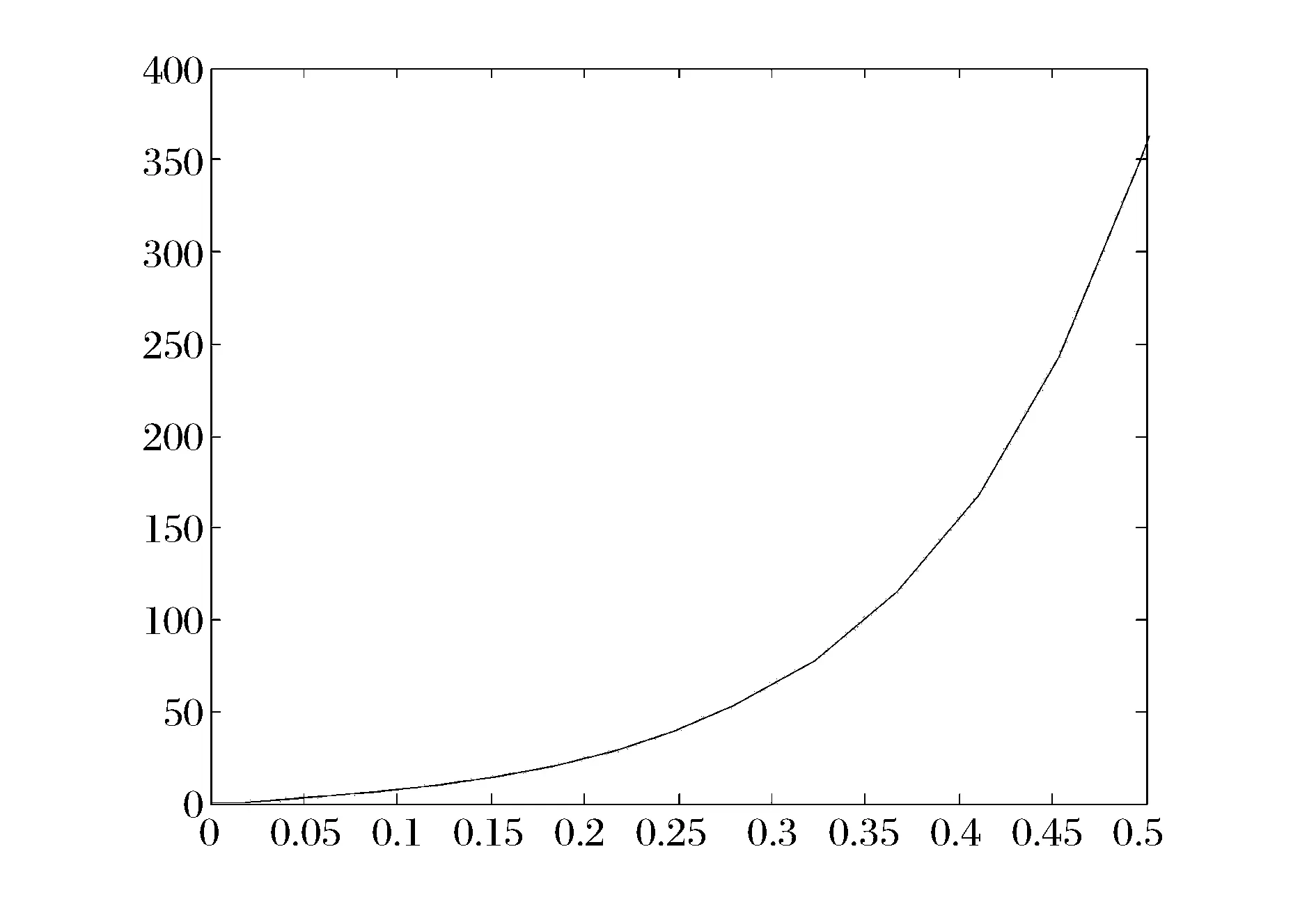
图4 λ=4时B1的解

图5 λ=4时B2的解

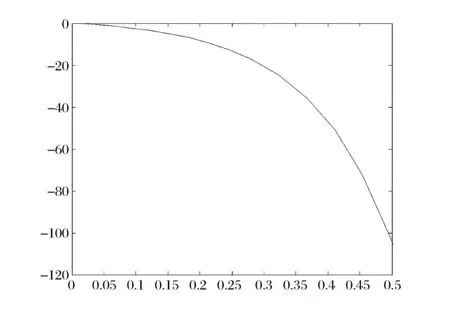
图6 λ=4时B3的解

将微分方程(9)—(14)式的解带入(15)可以得到对风险资产的最优投入策略。下面分析风险厌恶程度、不可观测的因素等对组合选择的影响。

首先分析风险厌恶程度对组合选择的影响。图7给出了λ=2和4时对两种风险资产的最优投资比例。

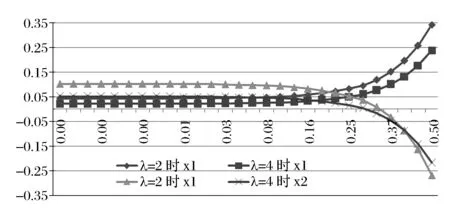
图7 不同风险厌恶程度对投资策略的影响

当投资时间在一定的范围内时，随着风险厌恶程度的增大，对风险资产的投入都会减少。但当投资超过一定时间时，随着风险厌恶程度的增大，对收益较大的资产人们反倒是会加大投入，表现出一种类似“赌博”的非理性投资方式。

当风险厌恶程度不变时，随着投资期的变长，对风险小的资产，投资者会增加投资比例；对风险大的资产，则会逐渐减少投入。

同时，图7也显示，当风险厌恶程度不变时，进行短期投资时，投资者关注收益，风险资产的收益越大投资比例越大；但进行长期投资时，投资者开始关注风险资产的波动率，他们会减少对风险大的资产的投入。同时，长、短期投资的转折点与投资者的风险厌恶程度有关，图7显示风险厌恶程度越大，这个转折时刻越小。

其次分析不可观测因素对投资组合选择的影响。表2、3给出了λ=4、λ=2时不可观测因素的存在对两种风险资产的投资比例的影响。

不考虑不可测因素时，同样有随着风险厌恶程度的增大，对风险资产的投入都会减少。

不论风险厌恶程度如何，对收益较小、风险较小的资产，投资者会逐渐增加对其的投入，并且对不可观测因素的了解导致随着投资期的越长，投资者越会增加投入。对收益较大、风险较大的资产，投资者会逐渐减少对其的投入，但在短期投资内，对不可观测因素的了解导致对此资产的投入增加；但长期投资时，不考虑不可观测因素的投资反而超过了考虑不可观测因素时的投资，这个转折点同样与投资者的风险厌恶程度有关，风险厌恶程度越大，转折时刻越小。

同时不可观测因素的存在，使得投资者对风险资产投入比例的变动幅度随风险厌恶程度的增加而增大。

最后分析贝叶斯学习对投资组合选择的影响。主要考察了不可观测因素与风险资产的相关性对投资组合的影响。图8给出了λ=4贝叶斯学习对投资组合选择的影响。

可以看到，对收益较小、风险较小的资产，在相同的投资期内，相关性越大投入比例越大，并且随着投资期的变长，投资比例增加的越多。对收益较大、风险较大的资产，则相反。即，在相同的投资期内，相关性越大投入比例越小，并且随着投资期的变长，投资比例减少的越多。

表2 λ=4不可观测因素的存在对两种风险资产的投资比例的影响

表3 λ=2不可观测因素的存在对两种风险资产的投资比例的影响

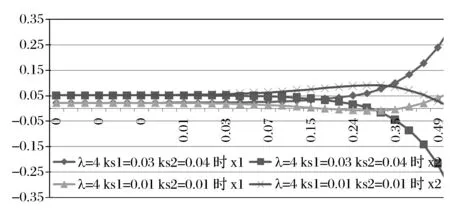
图8 λ=4贝叶斯学习对投资组合选择的影响

5 结语

收益与风险是投资者关心的两大问题，而有许多因素会影响资产的收益，有的因素可以观测到、而有的因素确不可以观测到。本文研究了金融市场中有一种无风险资产、两种风险资产，并且每种风险资产的超额收益中存在不可观测项，对应的风险既有系统性风险又有自身特有风险。对不可观测到的因素投资者根据已有的经验，利用贝叶斯学习过程进行调整，从而通过最优的投资策略使自己的最终财富达到最大。

假设投资者具有基于最终财富的、定常风险厌恶的幂效用函数，风险资产的价格服从一般的布朗运动，因此投资组合的收益就是一个随机过程，这样就构建了基于贝叶斯学习的动态投资组合优化模型，通过求解HJB方程，得到了对风险资产投入的最优策略，它与投资者的风险厌恶程度、投资期的长短、是否存在不可观测因素、学习过程等因素都有一定的关系。具体的数值分析表明，在一定的投资期限内，投资者表现出理性行为，即随着风险厌恶程度的增大，对风险资产的投入都会减少；但超过某一时刻，非理性的投资行为就会出现。当风险厌恶程度不变时，进行短期投资时，投资者关注收益，长期投资时，投资者开始关注风险资产的波动率。同时对不可观测因素的了解导致对收益较大、风险较大的资产，短期投资内增加其投入，而长期投资时，不存在不可观测因素的投资反而超过了存在不可观测因素时的投资。并且这个转折点随投资者的风险厌恶程度的增加而减小。不可观测因素与风险资产的相关性也使得对风险较小资产的投资比例与之成正比、风险较大资产的投资比例与之成反比。

[1] Kolm P N，Tutuncu R，Fabozzi F J，60 Years of portfolio optimization: Practical challenges and current trends [J].European Journal of Operational Research，2014，234(2)：356-371.

[2] Xia Yihong. Learning about predictability: The effects of parameter uncertainty on dynamic asset allocation [J]. Journal of Finance，2001，56 (1)：205-244.

[3] 袁子甲,李仲飞.参数不确定性和效用最大化下的动态投资组合选择[J].中国管理科学，2010，18(5)：1-6.

[4] Brandt M W, Goyal A, Santa-Clara P, et al.A simulation approach to dynamic portfolio choice with an application to learning about return predictability [J].The Review of Financial Studies，2005，18(3)：830-874.

[5] 杨朝军,陈浩武.参数不确定性对投资者最优资产组合的影响：基于中国的实证[J].中国管理科学，2008，16(3)：37-44.

[6] 陈志英.状态变化和学习行为下的最优资产组合选择[J].管理科学，2013，26(2)：81-90.

[7] Ando T，Bayesian portfolio selection using a multifactor model[J].International Journal of Forecasting，2009，25(3)：550-566.

[8] Virbickaite A, Ausin M C, Galeano P. A Bayesian non-parametric approach to asymmetric dynamic conditional correlation model with application to portfolio selection[J].Computational Statistics and Data Analysis，2016,100:814-829.

[9] Zhu Shushang, Fan Minjie，Li Duan.Portfolio management with robustness in both prediction and decision: A mixture model based learning approach[J].Journal of Economic Dynamics & Control，2014，48：1-25.

[10] Fama E F，French K R.Permanent and temporary components of stock prices [J]. Journal of Political Economy， 1988，96 (2)：246-273.

[11] Boudoukh J，Michaely R，Richardson M，et al.On the importance of measuring payout yield: Implications for empirical asset pricing [J].Journal of Finance， 2007，62 (2)：877-916.

[12] Drechsler I，Yaron A. What’s vol got to do with it[J]. Review of Financial Studies，2011，24 (1)：1-45.

[13] Ang A, Bekaert G.Stock return predictability: Is it there? [J].Review of Financial Studies，2007，20 (3)： 651-707.

[14] Lettau M，Van Nieuwerburgh S.Reconciling the return predictability evidence [J]. Review of Financial Studies，2008，21 (4)：1607-1652.

[15] Brennan M J.The role of learning in dynamic portfolio decisions [J].European Finance Review， 1998，1(3):295-306.

[16] Branger N， Larsen L S，Munk C.Robust portfolio choice with ambiguity and learning about return predictability[J].Journal of Banking & Finance，2013,37(5)：1397-1411.

[17] Liptser R S，Shiryaev A N.Statistics of random processes [M]. New York-Hedelberg: Springer-Verlag，1978.

[18] Jacquier E. Polson N，Bayesian methods in finance [M]//Geweleke J,Koop G,Van Dijk H.The Oxford handbook of Bayesian econometrics.Oxfor:Oxford University Press,2011.

Dynamic Portfolio Choice based Bayesian Learning Approach

GUO Wen-ying

(School of Statistics Capital University of Economics and Business, Beijing 1000070,China)

In this paper, the optimal dynamic portfolio choice is analyzed under Bayesian learning. Assuming that there are two kinds of risky assets, the returns of each asset are predictable by unobservable predictor, and risks of each asset have both systematic and own risks. The empirical results highlight that the proportion of the investor’s wealth invested in every risky asset is decreasing with the degree of risk aversion over short horizon, but it is opposite when the investment horizon is long. When the degree of risk aversion is constant, the Bayesian learning makes different about the long and short-horizon investment strategy. This critical point decreases with the degree of risk aversion of investor. The correlation between risk assets and the unobservable predictor is inversely proportional to the size of the risk of asset.

Bayesian learning; HJB equation; dynamic portfolio choice

1003-207(2017)08-0039-07

10.16381/j.cnki.issn1003-207x.2017.08.005

2015-10-13；

2016-11-21

国家自然科学基金资助项目(11371001)；首都经济贸易大学科研水平提高定额项目

郭文英(1967-)，女(汉族)，北京人，首都经济贸易大学统计学院，教授，博士，研究方向：数理金融，E-mail:guowy67@126.com.

F830

A