我国固定资产投资的ARIMA模型及其预测

谢婧芸

【摘 要】本文选取了1980-2015年我国全社会固定资产投资的相关数据作为研究样本，从时间序列的定义出发，结合统计软件R，对1980-2013年的数据建立ARIMA模型，并以2014-2015年的数据作为参照，判断模型的拟合效果，进而对2016-2018年固定资产投资进行预测。

【关键词】时间序列分析；单位根检验；ARIMA模型；预测

一、引言

改革开放以来，随着我国经济高速发展，我国全社会固定资产投资也以很大的增量快速增长，从1980年的910.9亿元猛增到2015年的561999.83亿元。本文没有考虑影响固定资产投资的其他因素，因为其影响因素很多并且相关性很高，研究起来很复杂，因此本文从动态的角度考虑，研究固定资产投资的时间序列，建立自回归移动平均模型，通过模型预测值与真实值比较来判断模型拟合的效果，并给出今后几年数据的预测值，可以作为固定资产投资的一个参考数据。

二、实证研究及其分析

1.数据收集

本文选择的变量为全社会固定资产投资，选择了1980-2015年的数据进行分析，数据来源于CSMAR数据库。为了检验模型的准确性，本文选择1980-2013年的34个数据进行建模，并通过比较2014-2015年的预测值和真实值来检验拟合效果，最后对2016-2018年的我国固定资产投资进行预测。

2.数据的平稳性检验

通过做时间序列图我们发现，原始数据的时间序列图随时间变化剧烈，不平稳，因此我们对原始数据进行对数处理，记为lnfi。通过对处理过后的对数数据进行ADF检验，得到lnfi的一阶差分平稳，记为dlnfi，因此我们选定dlnfi进行建模。

在ARIMA模型中，我们已经确定了d=1，下面我们通过EACF方法来确定模型的p和q，EACF结果输出如下：

3.模型建立

在ARIMA模型中，我们已经确定了d=1，下面我们通过EACF方法来确定模型的p和q，EACF结果输出如下：

AR/MA

0 1 2 3 4 5

0 oooooo

1 x o oooo

2 x o oooo

3 xx o ooo

4 xx o ooo

5 x o oooo

我们尽量选择数量小并且符合模型要求的阶数，因此我们选择p=1，q=1。

通过运行R软件建立ARIMA（1，1，1）模型，得到的变量均不显著，没有通过检验。在经过我们多次尝试反复筛选，选择出了拟合效果较好并且模型较简单的模型，最后我们建立ARIMA（2，1，1）模型，各项系数均通过显著性检验。

模型形式如下：

dlnfi=0.1871+1.2931dlnfi（-1）-0.623dlnfi（-2）-ξ（-1）

该模型各个变量的系数均通过t检验，说明各个系数都显著，模型拟合效果较好。

4.模型诊断

我们在R里得到的标准残差图，残差的ACF图以及LjungBox的P值結果可以看出模型检验结果良好，可以说明模型拟合得比较成功。

5.预测

下表给出了根据模型得出的2014-2018年固定资产投资的预测值以及2014-2015年预测的相对误差。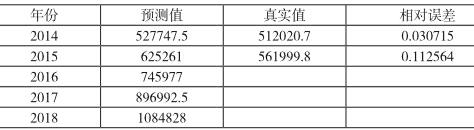

从上表可以看出，2014年预测结果的相对误差小于5%，结果相当令人满意，但是2015年预测结果的相对误差为11%，效果不理想。说明ARIMA模型在很短期内预测比较准确，随着预测的延长，预测误差会逐渐增大，这是ARIMA模型的缺陷。同时也说明，我们建立的模型仍然不是最佳模型，还需要很多改进和完善的地方，没能很好的反映数据的特征，因此没能得到最佳的预测效果。

三、结论

在模型选择方面，通过以上分析我们选择了ARIMA（2，1，1）模型。可以看出，我国固定资产投资是一阶单整的，当期固定资产投资受到上一期固定资产投资，上上一期固定资产投资，当期扰动项以及上一期扰动项的影响。这说明之前两期的固定资产投资对当期固定资产投资的冲击是有效的持久的，因此国家在配置固定资产投资时，要保证固定资产投资平稳高效，建议政府在引导投资时应合理安排投资比例，合理运用投资金额和投资机会，从而促进经济健康发展。

在预测方面，我们对2014-2018年固定资产投资进行预测，可以看出在2018年全社会固定资产投资有望突破100万亿元。从预测的效果来看，我们对2014年固定资产投资的预测较为精确，但是对2015年固定资产投资预测偏差较大，造成预测精度不高的原因，一方面是固定资产投资容易受到其他多方面的因素的影响，比如国家政策，经济发展水平，价格变动等因素，不确定性增加；另一方面可能是样本数量不多，降低了预测的精度。同时ARIMA模型本身也有缺陷。

参考文献：

[1]王周伟，崔百胜，朱敏等，编著.经济计量研究指导：实证分析与软件实现[M]，北京大学出版社，2015.4.

[2]冯建中，周德强.基于因子分析的全社会固定资产投资竞争力研究[J]，改革与战略，2010，26（8）.

[3]师思.ARIMA模型在固定资产投资变化率预测中的运用[J]，统计与决策，2009（10）.endprint