关于椭圆曲线y2=nx(x2-4)的整数点的一个注记

陈进平

(1.阿坝师范学院 数学与财经系，汶川 623000；2.儋州市思源高级中学，海南 儋州 571700)

关于椭圆曲线y2=nx(x2-4)的整数点的一个注记

陈进平

(1.阿坝师范学院 数学与财经系，汶川 623000；2.儋州市思源高级中学，海南 儋州 571700)

运用四次Diophantine方程的性质以及初等方法证明了：设p是素数,当p≢1(mod 8)时,方程y2=px(x2-4)仅有正整数解(p,x,y)=(3,4,12),(7,16,168),(3,98,1680)(3,6,24),(11,198,9240).若p≡1(mod 8)时，方程y2=px(x2-4)至多有一组正整数解.指出了万飞文章中的错误，并利用初等方法巧妙得出了一些新的结论，改进了Wenguan Wu,Alain Togb'e,Bo He,Shichun Yang等的解的个数的上界.

丢番图方程；解数；整数解

1 引言与主要结论

设Z，N分别是全体整数和正整数的集合，n是大于1的无平方因子正数，椭圆曲线：

y2=nx(x2-4),x,y∈N

(1)

椭圆曲线的整数点是数论和算数代数几何中基本而又重要的问题.而关于椭圆曲线y2=nx(x2-4)的整数点问题，吴文权,Alain Togbe,何波,杨仕椿[1]证明了：设n是无平方正整数和A>1的奇数,则方程y2=n(Ax2-4)最多有2w(n)+2解(x,y).当n=p是奇素数时，则方程y2=px(Ax2-4)最多有8个解(x,y).文献[2]证明了如果n为奇素数时，则椭圆曲线y2=nx(x2-4)至多有一个整数点.本文指出文献[2]中的结论和失误,并给出了若p=3时，则方程y2=3x(x2-4)的正整数解为(x,y)=(4,12),(98,1680),(6,24).给出了文献[2]结论的错误性.本文主要讨论当n=p是素数时方程(1)的整数点，运用四次Diophantine方程的性质以及初等方法证明了方程(1)至多有三个正整数解,因此纠正了文献[2]的结果，改进了文献[1]解的个数的上界.在此类领域的文章[3-7]也得到了很好的成果.

定理1 对于素数p，方程:

y2=px(x2-4)

(2)

方程(2)至多有三个正整数解.当p≢1(mod 8)时，方程(2)仅有正整数解(p,x,y)=(3,4,12),(7,16,168),(3,98,1680)(3,6,24),(11,198,9240).若p≡1(mod 8)时，方程(2)至多有一组解.

2 主要引理

引理1[8]设p为奇素数，则方程x4-2py2=1仅有正整数解(p,x,y)=(3,7,20).

方程4x4-py2=1仅有正整数解(p,x,y)=(3,1,1),(7,2,3).

引理2[9]设p≢1(mod 8)为奇素数，则丢番图方程p2x4-8y2=1仅有正整数解(p,x,y)=(3,1,1),(11,3,35).

证明：由文献[4]的引理4可得.

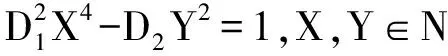
3 定理的证明

设(x,y)是方程(2)的解，因为gcd(x,x2-4)=1,2,4.

当x≡1,3(mod 4)时，则gcd(x,x2-4)=1.由方程(2)可得:

x=a2,x2-4=pb2,y=abp,(a,b)=1

(3)

或

x=pb2,x2-4=a2,y=abp,(a,b)=1

(4)

(这里的a,b都为奇数)

当式(3)成立时，由式(3)得：a4-pb2=4,所以(a2-2)(a2+2)=pb2,因为a,b都为奇数，所以(a2-2,a2+2)=1.因此，可以分成以下两种情况：

(5)

或

(6)

当x≡2(mod 4)时，则gcd(x,x2-4)=2，则由方程(2)得：

x=2a2,x2-4=2pb2,(a,b)=1

(7)

或

x=2pb2,x2-4=2a2,y=2pab,(a,b)=1

(8)

当式(7)成立时，有2a4-pb2=2.当p=2时，得a4-b2=1，解得无正整数解.因此，得出p≥3为奇素数，易知2|b，则b=2b1，其中b1是任意正整数.得出：

a4-2pb12=1

(9)

由引理1得方程(9)仅有正整数解(p,a,b1)=(3,7,20)，所以(p,a,b)=(3,7,40)代入式(7)得(p,x,y)=(3,98,1680).

当式(8)成立时，有

2p2b4-a2=2

(10)

由式(10)得：2|a，则a=2a1，其中a1是任意正整数.所以(10)式可以转化为：

p2b4-2a12=1

(11)

若a1为奇数时.由式(11)易得出p是奇素数，所以p2≡1(mod 8).则由式(11)可得.p2≡3(mod 8)与p2≡1(mod 8)矛盾.所以a=4a2,a1=2a2，其中a2是任意正整数.所以式(10)可以转化为：

p2b4-8a22=1

(12)

若p≢1(mod 8)时，由引理2得：式(12)仅有整数解(p,b,a2)=(3,1,1),(11,3,35).所以(p,b,a)=(3,1,4),(11,3,140)代入式(8)得(p,x,y)=(3,6,24),(11,198,9240).

当p≡1(mod 8)时，由引理3知：式(12)至多有一组解，则式(10)至多有一组解.

当x≡0(mod 4)时，gcd(x,x2-4)=4，则由方程(2)得：x=4a2,x2-4=4pb2,y=4pab,(a,b)=1

(13)

或

x=4pb2,x2-4=4a2,y=4pab,(a,b)=1

(14)

由式(13)成立时，得出4a2-pb2=1，由引理3得仅有正整数解(p,a,b)=(3,1,1),(7,2,3)，所以(p,x,y)=(3,4,12),(7,16,168).

当式(14)成立时,得出(2pb2)2=a2=1,易解得无正整数解,所以式(14)无正整数解.

综上所述，可得对于任何素数p，方程(2)至多有三个正整数解.当p≢1(mod8)时，方程(2)仅有正整数解(p,x,y)=(3,4,12),(7,16,168),(3,98,1680),(3,6,24),(11,198,9240).

若p≡1(mod8)时，方程(2)至多有一组解.若p=3时，则方程y2=3x(x2-4)的正整数解为(x,y)=(4,12),(98,1680),(6,24).

(致谢：衷心感谢阿坝师范学院数学与财经系研究所杨仕椿教授的悉心指导和热情鼓励并提供了文献[1]的文章)

[1]WENQUANWu,AlainTogb′e,BoHe,ShichunYang，OnthenumberofsolutionsoftheDiophantineequationy2=nx(Ax2±C)[J].SPacJpureapplmath.2013，2(2)：1-16.

[2] 万飞.椭圆曲线y2=nx(x2-4)的整数点[J].湖北民族学院学报(自然科学版),2015,33(3):271-272.

[3] 祝辉林，陈建华.两个丢番图方程y2=nx(x2±1)[J].数学学报(中文版),2007,50(5):1071-1074.

[4] DRAZIOTIS K.Integral solutions of the equationY2=X3±pkX[J].Math Comp,2006,255(75):1493-1505.

[5] DRAZIOTIS K,POULAKIS D.Practical solution of the Dionphantine equationy2=x(x+2apb)(x-2apb)[J].Math Comp，2006,255(75):1585-1593.

[6] FENG K,XIONG M.On elliptic curvesy2=x3-n2xwith rang zero[J].Number Theory,2004,109:1-26.

[7] DRAZIOTIS K.POULAKIS D.Solving the Diophantine equationy2=x(x2-n2)[J].J Number Theory,2009,129:102-121.

[8] 曹珍富.丢番图方程引论[M].哈尔滨：哈尔滨工业大学出版社,2012:180-187.

[9] 王云葵.关于LUCAS猜想的推广形式[J].华侨大学学报,2001，22(3):242-246.

[10] BENNETT M A,WALSH G.The Diophantine Equationb2X4-dY2=1[J].Proc Amer Math Soc,1999,127(12):3481-3491.

责任编辑：时 凌

A Note on the Integral Points on the Elliptic Curvey2=nx(x2-4)

CHEN Jinping

(1.Department of Mathbematics and Finnance,Aba Teachers University, Wenchuan 623000,China; 2.Danzhou Siyuan Senior High School,Danzhou 571700,China)

In this paper, the properties of quartic Diophantine equations and elementary method are used to prove:let p be a prime, whenp≢1(mod 8),(p,x,y)=(3,4,12),(7,16,168),(3,98,1680)(3,6,24),(11,198,9240) are the only positive integer solutions of equationy2=px(x2-4).Ifp≡1(mod 8),the equationy2=px(x2-4) has no more than a set of positive integer solutions.The essay points out the mistakes in the documentary by Wan Fei.And meanwhile,using primary methods,the author skillfully drew some new conclusions and imprve the upper bounds of the number of solutions in documentaries by Wenguan Wu,Alain Togb′e,Bo He,Shichun Yang.

Diophantine equation;solution number;integer solution

2017-03-21.

海南省教育科学规划专项课题(QJH1251533);海南省高考综合改革重点课题(QJZ13517016).

陈进平(1990-),男，二级教师，主要从事数论的研究.

1008-8423(2017)03-0290-02

10.13501/j.cnki.42-1569/n.2017.09.010

O156.7

A