X形柔性铰链等效刚度分析及结构特性研究*
邱丽芳,王栋,印思琪,杨德斌
(北京科技大学 机械工程学院,北京 100083)
X形柔性铰链等效刚度分析及结构特性研究*
邱丽芳,王栋,印思琪,杨德斌†
(北京科技大学 机械工程学院,北京 100083)
基于抗压双片段柔性铰链,设计了4片段X形柔性铰链,并对其结构特性进行了研究.X形柔性铰链中的主要变形片段为弯扭耦合片段,分别运用微分法和基于抗压双片段柔性铰链等效刚度算法分析了其弯扭耦合等效刚度,推导出了X形柔性铰链的等效刚度理论计算公式.设计了几组不同尺寸的X形柔性铰链实例,分别利用2种方法对这些实例进行了计算,并在ABAQUS软件中进行了仿真分析,3种分析方法结果表明了理论计算公式和仿真模型的正确性.最后,通过对不同尺寸的X形柔性铰链结构特性的分析,得到了铰链设计时应该尽量避免的结构参数范围.
柔性铰链;弯扭耦合;等效刚度;微分法;结构特性
平面折展机构(Lamina emergent mechanisms,LEMs)是柔顺机构的一种,由薄板材料加工制成,可实现平面外运动.LEMs是通过柔性部件的弹性变形来完成运动的,每一个平面层都具有整体性[1].它集合了正交机构、变胞机构和柔顺机构的特性[2],具有能提高精度、降低重量、无间隙、减少磨损和构件数等柔顺机构的优点[3].此外,还具有减少装配时间、简化加工工序以及降低振动和噪声、节省运输空间等优点[4],能实现四杆机构、滑块机构、球面机构、斯蒂芬森机构等运动[5-7].柔性机构的应用领域十分广泛,文献[8]将柔性机构的主体应用划分为精密工程、仿生机器人和智能材料结构三大主阵地;文献[9]设计一种新型的柔顺剥线钳;文献[10]中设计了一种柔性可回程扳手;文献[11]设计了一种具有多种功能的不同大小形状的信用卡机械机构.尽管柔性机构具有很多优势,但其变形运动范围经常受到限制,而且相比刚性机构,它的设计难度更大[12-14].
LEMs实现特性和发挥优势的关键在于柔性铰链.对于LEMs柔性铰链而言,几何尺寸、边界条件、材料特性等是影响其功能特性的关键因素[15].Jacobsen等[16]提出了关于LET柔性铰链等效刚度的理论计算公式; Ferrell等[17]设计了两种柔性铰链——RUFF柔性铰链和TUFF柔性铰链;Delimont等[18]总结概括部分柔性铰链等效刚度的理论计算公式;Delimont等[19]设计提出了一系列双片段的柔性铰链,并推导了其等效刚度计算公式;文献[20]提出了一种新型S形柔性铰链的等效刚度的理论计算公式.据作者所查文献,研究LEMs柔性铰链的等效刚度理论计算公式时,大部分定义为弯曲片段、扭转片段或者连接片段.
本文基于文献[19]中的双片段柔性铰链(Mixed Tension Resistant)类型衍生设计了四片段X形柔性铰链,定义其主要的变形片段为弯扭耦合片段,运用微分的思路分析了其弯扭耦合等效刚度,并对其结构特性进行了研究分析.
1 X形柔性铰链的设计
基于双片段柔性铰链(Mixed Tension Resistant)类型衍生出四片段X形柔性铰链,其三维结构图如图1所示,该铰链的长度为l0,宽度为w0,厚度为t0.
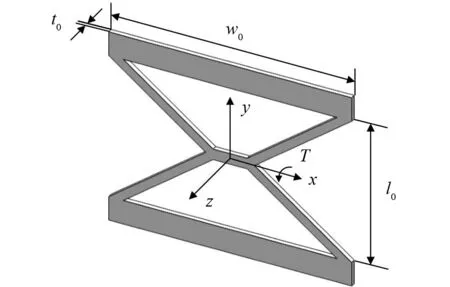
图1 X形柔性铰链三维结构图Fig.1 3D model of X-shaped flexure hinge
X形铰链可以分解为3部分,根据铰链在转动变形过程中所产生的变形不同,分为连接片段、弯扭耦合片段和弯曲片段,各个片段的位置如图2所示.在铰链受力时,图中A,B,C,D片段发生弯曲变形和扭转变形的程度相当,可以视为弯扭耦合片段,E片段主要为弯曲变形,所以视为弯曲片段.
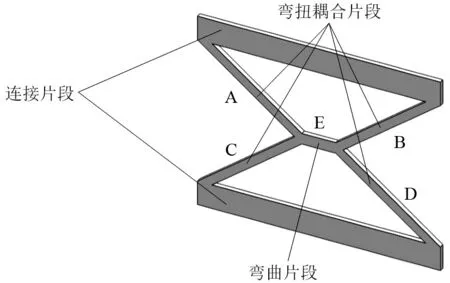
图2 X形柔性铰链片段示意图Fig.2 The segments of X-shaped flexure hinge
各个片段的尺寸如图3所示,A,B,C,D片段的尺寸相同,长度为l1,宽度为w1,厚度为t0;E片段的长度为l2,宽度为w2,厚度为t0,弯扭耦合片段与y轴的夹角为α.
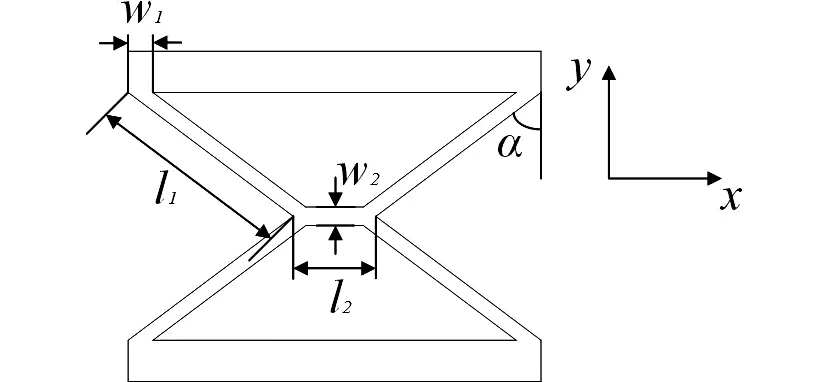
图3 X形柔性铰链片段尺寸示意图Fig.3 Dimension labels of X-shaped flexure hinge
2 X形柔性铰链的等效刚度分析
2.1 微分法
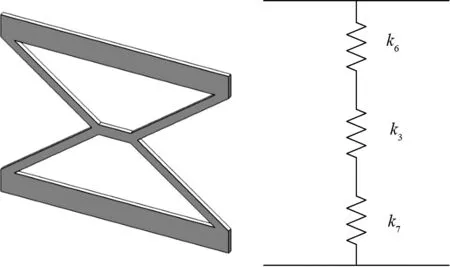
根据柔性铰链的弹簧等效法,将X形柔性铰链的A,B,C,D片段和E片段分别等效为弯扭弹簧和弯曲弹簧,根据弹簧的串并联关系,即可得到X形柔性铰链的等效弹簧模型,如图4所示.
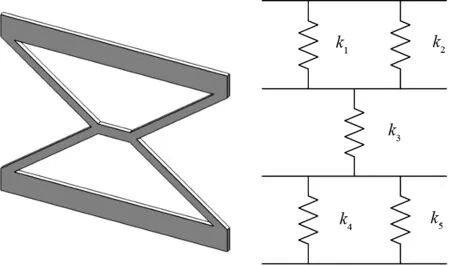
图4 微分法的X形柔性铰链等效弹簧模型图Fig.4 The associated spring model of X-shaped flexure hinge with differential method
根据弹簧串并联关系,可以得到X形柔性铰链在转动时的等效刚度:
(1)
由于A,B,C,D片段均为弯扭耦合片段,且尺寸相同,则有:
k1=k2=k4=k5=kBT
(2)
根据式(1)和式(2)可以得到
(3)
下面分别计算kBT和k3.
对于弯扭耦合片段而言,没有现成的公式可以计算其等效刚度kBT,但可以利用微积分的思想分别求解弯曲等效刚度kB和扭转等效刚度kT,再将其进行耦合,即可得到弯扭耦合片段的等效刚度kBT.建立如图5所示坐标系,取出一个弯扭耦合片段进行计算,设材料的弹性模量为E,泊松比为v.
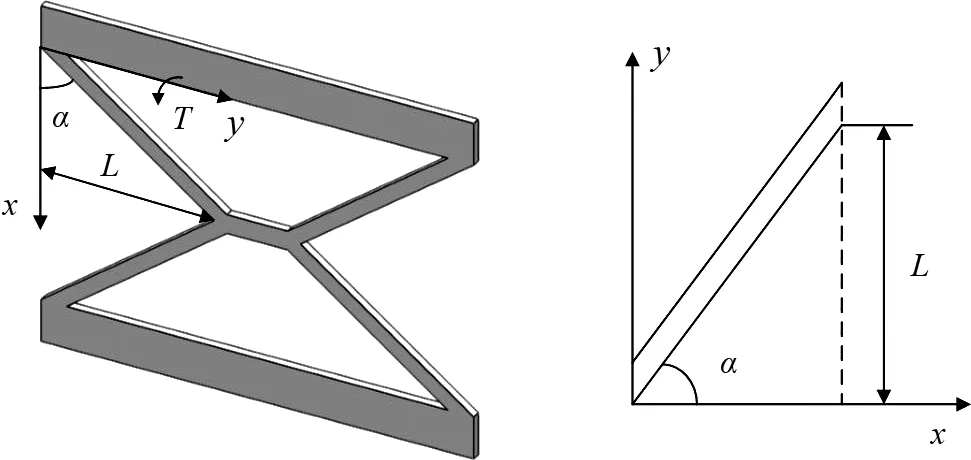
图5 弯扭耦合片段的坐标示意图Fig.5 X-Y plot of bending-torsional coupling segment
计算弯曲等效刚度kB,设弯扭耦合片段在转矩T作用下弯曲变形转角为θB,其微分图如图6所示.
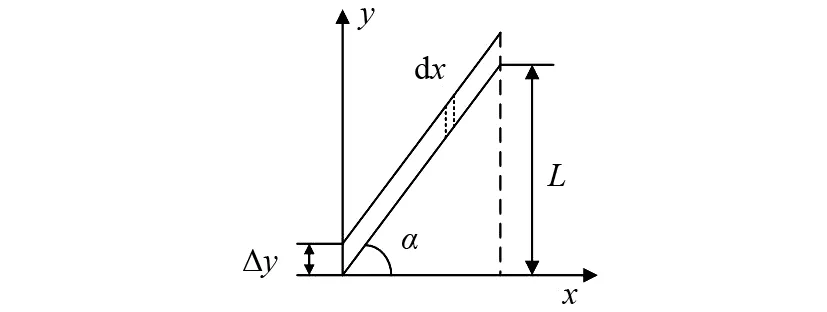
图6 弯扭耦合片段弯曲变形转角的微分示意图Fig.6 Differential diagram of bending angle in bending-torsional coupling segment
Δy=w1
(4)
(5)
(6)
(7)
(8)
计算弯曲等效刚度kT,设弯扭耦合片段在转矩T作用下扭转变形转角为θT,其微分图如图7所示.

图7 弯扭耦合片段扭转变形转角的微分示意图Fig.7 Differential diagram of torsional angle in bending-torsional coupling segment
由于弯扭耦合片段的结构特殊性,扭转等效刚度需要分为3个区间进行计算:
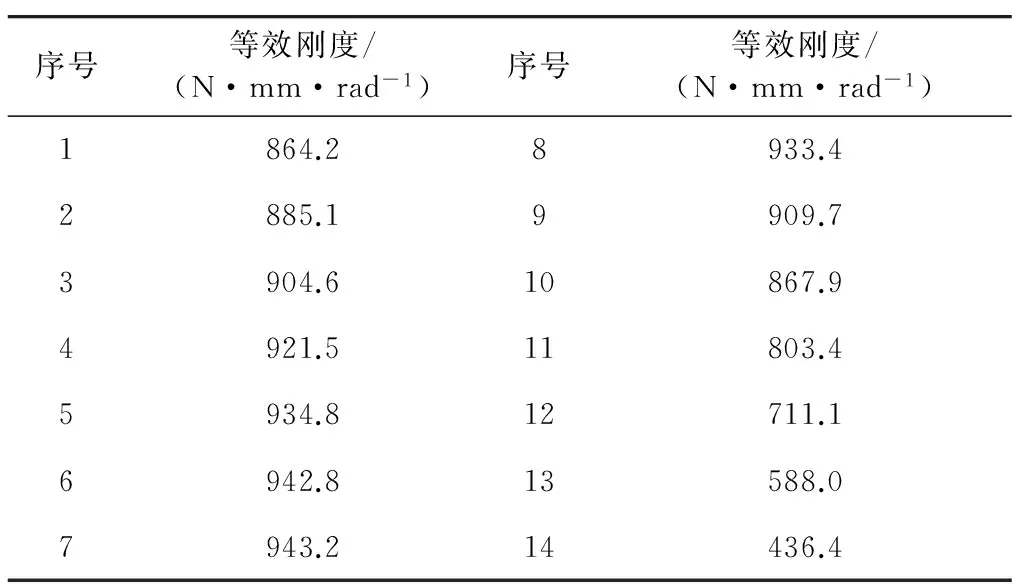
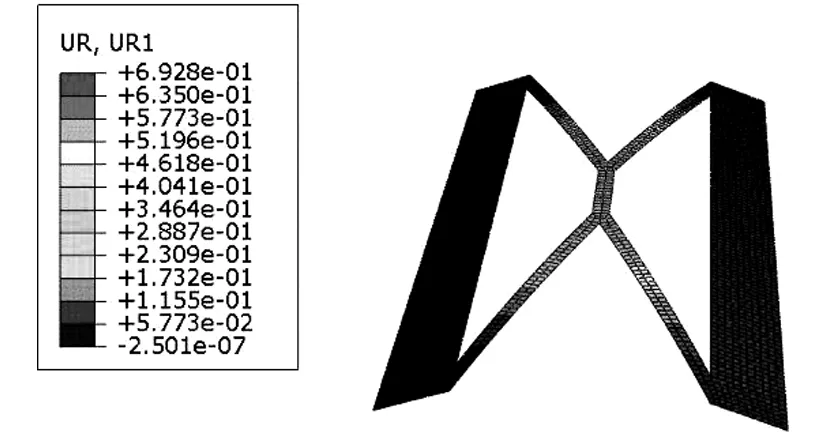
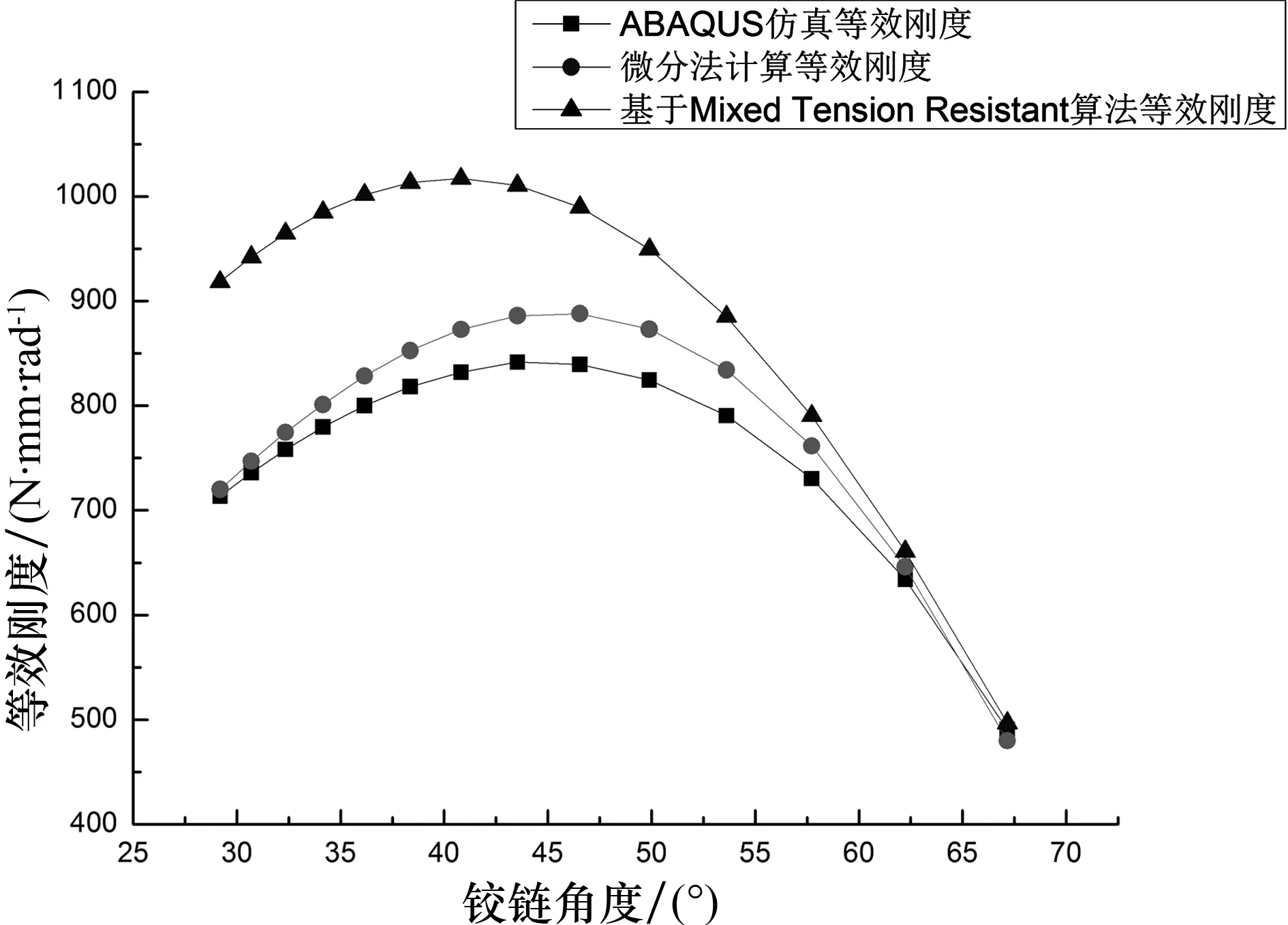
1)当0 由于在0 (9) 2)当w1 Δx=w1cotα (10) (11) (12) (13) (14) 3)当L 由于在L (15) 在式(9)和式(15)中出现的Ki,Young等[21]给出了Ki的近似公式: (16) Lobontiu等[22]忽略了高次项,将式(16)简化为: (17) 式中:LTw为扭转片段的宽度,t为铰链的厚度,在本文中LTw=w1cotα,t=t0,则 (18) (19) 式中G为剪切模量,表示为: (20) 根据弹簧等效耦合关系有: (21) 由式(14),(19)和(21)可以得出弯扭耦合片段的扭转等效刚度kT为: (22) 根据弹簧等效耦合关系有: (23) 由式(8),(22)和(23)即可得出弯扭耦合片段的等效刚度: (24) 对于E片段,视其为弯曲片段,可由以下公式计算得出其弯曲刚度 (25) (26) 将式(24)和(26)代入式(3)即可得到keq. 2.2 基于Mixed Tension Resistant算法 根据文献[19]中对于Mixed Tension Resistant构型的柔性铰链推导出的等效刚度理论计算公式,结合弹簧等效法,可以将X形柔性铰链的等效为如图8所示弹簧模型. (27) kBm(cosα)2+kTm(sinα)2 (28) (29) (30) 由式(27)和(28)可以得到: (31) 图8 基于Mixed Tension Resistant的等效弹簧模型Fig.8 The associated spring model of X-shaped flexure hinge with Mixed Tension Resistant method 选取铍青铜作为X形柔性铰链的材料,铍青铜性能参数如表1所示. 表1 铍青铜的性能参数Tab.1 Performance parameters of beryllium bronze 设计X形柔性铰链的宽度w0为50 mm,厚度t0为1 mm,片段E长度l0为10 mm,考虑铰链的尺寸不能过大,保持铰链的结构特性,E片段的宽度w2不能小于厚度t0,故铰链长度l0在68 ~16 mm之间选取了14组数据,具体参数如表2所示. 表2 X形铰链实例尺寸Tab.2 The size of X-shaped flexure hinge examples 3.1 基于Mixed Tension Resistant算法 利用微分法计算上述不同尺寸X形柔性铰链的等效刚度,得到结果如表3所示. 表3 微分法计算的等效刚度Tab.3 The equivalent stiffness calculated by differential method 利用基于Mixed Tension Resistant的等效刚度算法计算上述不同尺寸X形柔性铰链的等效刚度,得到结果如表4所示. 3.2 有限元仿真及数据分析 在ABAQUS中建立以上14个尺寸X型柔性铰链的有限元仿真模型,分别加载300 N·mm的转矩,得到每个铰链的角位移云图,其中序号为14的角位移云图如图9所示.仿真得到转角值及计算得到的等效刚度如表5所示. 表4 基于Mixed Tension Resistant算法计算的等效刚度Tab.4 The equivalent stiffness calculated by Mixed Tension Resistant method 图9 X形铰链实例的角位移云图Fig.9 FEA model of the X-shaped flexure hinge showing the stress in bending condition 序号转角/radkeq/(N·mm·rad-1)序号转角/radkeq/(N·mm·rad-1)10.4302697.3580.3744801.2820.4181717.5390.3777794.2830.4069737.28100.3876773.9940.3966756.42110.4078735.6550.3878773.59120.4476670.2460.3808787.81130.5232573.3970.3758798.29140.6928433.02 根据上述仿真得到的等效刚度和两种理论计算的等效刚度数据对比图如图10所示. 图10 l2为10 mm的等效刚度数据对比图Fig.10 Data comparison of the equivalent stiffness 10 mm in length of l2 由图10和表3、表4、表5中的数据可以得到,在X形铰链其他尺寸保持不变的情况下,当铰链角度30°<α<61°时,微分法计算的等效刚度与ABAQUS仿真得到的等效刚度之间的误差小于5%,而基于Mixed Tension Resistant算法计算的等效刚度与ABAQUS仿真得到的等效刚度之间误差大于5%;当铰链角度61°<α<71°时,微分法和基于Mixed Tension Resistant算法计算的等效刚度与ABAQUS仿真得到的等效刚度之间的误差均在5%以内.文献[16]中提到式(17)的适用条件为LTw>t,文献[19]中提到式(30)的适用条件为w1cosα>t0,当铰链角度α≥71°时,w1cosα 为进一步验证微分法和基于Mixed Tension Resistant算法的正确性,在保证铰链宽度w0为50 mm,厚度t0为1 mm不变的情况下,改变片段E长度l2为12 mm,同样在铰链长度l0在68~16 mm之间选取了14组数据,分别利用微分法和基于Mixed Tension Resistant算法进行等效刚度的计算,并在ABAQUS中建立模型进行仿真分析,最后绘制等效刚度数据对比图如图11所示. 图11 l2为12 mm的等效刚度数据对比图Fig.11 Data comparison of the equivalent stiffness 12 mm in length of l2 图11中的曲线和图10曲线变化趋势基本一致,进一步验证了上述两种计算方法的误差范围,即可将上述情况描述如下:对于X形铰链等效刚度的计算,在保证其他尺寸不变的情况下,当铰链角度30°<α<11°时,利用微分法计算;当铰链角度61°<α<71°时,微分法和基于Mixed Tension Resistant算法均可;当铰链角度α≥71°时,现有的理论公式无法进行等效刚度的计算.并且在铰链角度42°<α<50°时,X形铰链的等效刚度同样为较大,即弯曲性能较差,设计时应尽量避免. 1)基于双片段柔性铰链中的Mixed Tension Resistant类型铰链衍生设计了X形柔性铰链,分析了其弯扭耦合等效刚度,分别利用微分法和基于Mixed Tension Resistant算法推导出了X形柔性铰链两种不同的等效刚度理论计算公式. 2)设计了几组不同尺寸的X形柔性铰链实例,并对其进行了理论分析和建模仿真,确定了微分法和基于Mixed Tension Resistant算法两种理论计算公式的适用范围:当铰链角度30°<α<61°时,利用微分法计算;当铰链角度61°<α<71°时,微分法和基于Mixed Tension Resistant算法均可;当铰链角度α≥71°时,现有的理论公式无法进行等效刚度的计算. 3)在X形柔性铰链其他尺寸保持不变的情况下,当铰链角度42°<α<50°时,铰链的等效刚度较大,其弯曲性能较差,设计中应该尽量避免选用铰链结构角度处于42°至50°之间的铰链. [1] JACOBSEN J O,HOWELL L L,MAGLEBY S P.Components for the design of lamina emergent mechanisms [C]//Proceedings of the ASME International Mechanical Engineering Congress and Exposition,IMECE 2007.New York:American Society of Mechanical Engineers,2008:165-174. [2] JACOBSEN J O,WINDER B G,HOWELL L L,etal.Lamina emergent mechanisms and their basic elements [J].Journal of Mechanisms and Robotics,2010,2(1):1-9. [3] PARISE J J,HOWELL L L,MAGLEBY S P.Ortho-planar linear-motion springs[J].Mechanism and Machine Theory,2001,36(11/12):1281-1299. [4] 王雯静,余跃庆,王华伟.柔顺机构国内外研究现状分析[J].机械设计,2007,24(6):1-4. WANG Wenjing,YU Yueqing,WANG Huawei.Analysis on the research status of compliant mechanism at home and abroad [J].Journal of Machine Design,2007,24(6):1-4.(In Chinese) [5] GOLLNICK P S,BLACK J D,SAVAGE E E,etal.A preliminary study of actuation approaches for lamina emergent mechanisms [C]// Proceedings of the ASME Design Engineering Technical Conference,IDETC/CIE 2011.New York:American Society of Mechanical Engineers,2011:191-202. [6] ATEN Q T,ZIRBEL S A,JENSEN B D,etal.A numerical method for position analysis of compliant mechanisms with more degrees of freedom than inputs [J].Journal of Mechanical Design,2011,133(6):061009. [7] WILDING S E,HOWELL L L,MAGLEBY S P.Spherical lamina emergent mechanisms [J].Mechanism and Machine Theory,2012,49:187-197. [8] 于靖军,郝广波,陈贵敏,等.柔性机构及其应用研究进展[J].机械工程学报,2015,51(13):53-68. YU Jingjun,HAO Guangbo,CHEN Guimin,etal.State-of-art of compliant mechanisms and their applications [J].Journal of Mechanical Engineering,2015,51(13):53-68.(In Chinese) [9] 达选祥,勾燕洁,陈贵敏.一种基于变胞变换的柔顺剥线钳[J].机械工程学报,2015,51(1):69-75. DA Xuanxiang,GOU Yanjie,CHEN Guimin.A compliant wire stripper based on metamorphic transformation [J].Journal of Mechanical Engineering,2015,51(1):69-75.(In Chinese) [10]马付雷,刘小院,陈贵敏.一种用于狭小操作空间的柔性可回程扳手[J].机械工程学报,2015,51(13):183-188. MA Fulei,LIU Xiaoyuan,CHEN Guimin.Design of a compliant reversible wrench for limited-space operations [J].Journal of Mechanical Engineering,2015,51(13):183-188.(In Chinese) [11]ALBRECHTSEN N B,MAGLEBY S P,HOWELL L L.Using lamina emergent mechanisms to develop credit-card-sized products [C]// Proceedings of the ASME Design Engineering Technical Conference,IDETC/CIE 2011.New York:American Society of Mechanical Engineers,2011:223-231. [12]SMITH S T.Flexures:elements of elastic mechanisms [M].Florida:CRC Press,2000:2-5. [13]LOBONTIU N.Compliant mechanisms:design of flexure hinges [M].Florida:CRC Press,2002:1-14. [14]HOWELL L L.Compliant mechanisms [M].New York:John Wiley & Sons,2001:6-8. [15]JACOBSEN J O,HOWELL L L,MAGLEBY S P.Components for the design of lamina emergent mechanisms [C]// Proceedings of the ASME International Mechanical Engineering Congress and Exposition,IMECE 2007.New York:American Society of Mechanical Engineers,2008:165-174. [16]JACOBSEN J O,CHEN Guimin,HOWELL L L,etal.Lamina Emergent Torsional (LET) joint [J].Mechanism and Machine Theory,2009,44(11):2098-2109. [17]FERRELL D B,ISAAC Y F,MAGLEBY S P,etal.Development of criteria for lamina emergent mechanism flexures with specific application to metals [J].Journal of Mechanical Design,2011,133(3):031009. [18]DELIMONT I L,MAGLEBY S P,HOWELL L L.Evaluating compliant hinge geometries for origami-inspired mechanisms [J].Journal of Mechanisms and Robotics,2015,7(1):011009. [19]DELIMONT I L,MAGLEBY S P,HOWELL L L.A family of dual-segment compliant joints suitable for use as surrogate folds [J].Journal of Mechanical Design,2015,137(9):92302. [20]邱丽芳,孟天祥,张九俏,等.平面折展机构S形柔性铰链设计与试验[J].农业机械学报,2014,45(9):324-328. QIU Lifang,MENG Tianxiang,ZHANG Jiuqiao,etal.Design and test of lamina emergent mechanisms S-shaped flexure hinge [J].Transactions of the Chinese Society for Agricultural Machinery,2014,45(9):324-328.(In Chinese) [21]YOUNG W C,BUDYNAS R G.Roark's formulas for stress and strain [M].7th Edition.New York:McGraw-Hill,2002:401-412. [22]LOBONTIU N,GARCIA E,CANFIELD S.Torsional stiffness of several variable rectangular cross-section flexure hinges for macro-scale and MEMS applications [J].Smart Materials and Structures,2004,13(1):12-19. Research on Equivalent Stiffness and Structure Characteristic of X-shaped Flexure Hinge QIU Lifang,WANG Dong,YIN Siqi,YANG Debin† (School of Mechanical Engineering,University of Science and Technology Beijing,Beijing 100083,China) Based on compressed double segment flexure hinge,the four segment X-shaped flexure hinge was designed,and its structure characteristic was studied.As the major deformation segment of X-shaped flexure hinge is bending-torsional coupling segment,the analysis on the equivalent stiffness of bending torsion coupling was performed by differential method and the method based on compressed double segment flexure hinge,and the theoretical calculation formula of the equivalent stiffness of X-shaped flexure hinge was derived.Several examples of X-shaped flexure hinge with different sizes were presented,the equivalent stiffness of these examples was calculated by two calculation formulas,and the simulation analysis on these examples was then carried out through ABAQUS software.The results of the three methods have showed the correctness of the theoretical calculation formula and the simulation model.Finally,the range of structural parameters that should be avoided when designing the hinge was obtained by the analysis of the structure characteristic. flexure hinge;bending-torsional coupling;equivalent stiffness;differential method;structure characteristic 1674-2474(2017)08-0063-07 10.16339/j.cnki.hdxbzkb.2017.08.010 2016-07-26 国家自然科学基金资助项目(51475037),National Natural Science Foundation of China(51475037) 邱丽芳(1966-),女,浙江嘉兴人,北京科技大学教授 †通讯联系人,E-mail:ydb@ustb.edu.cn TH122 A
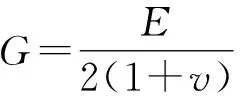
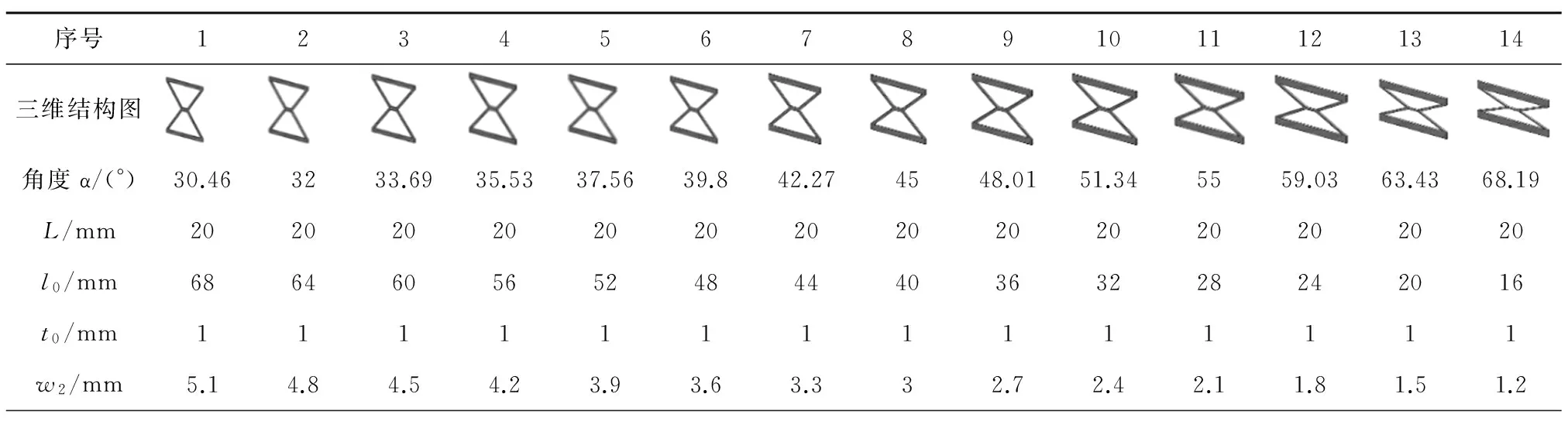
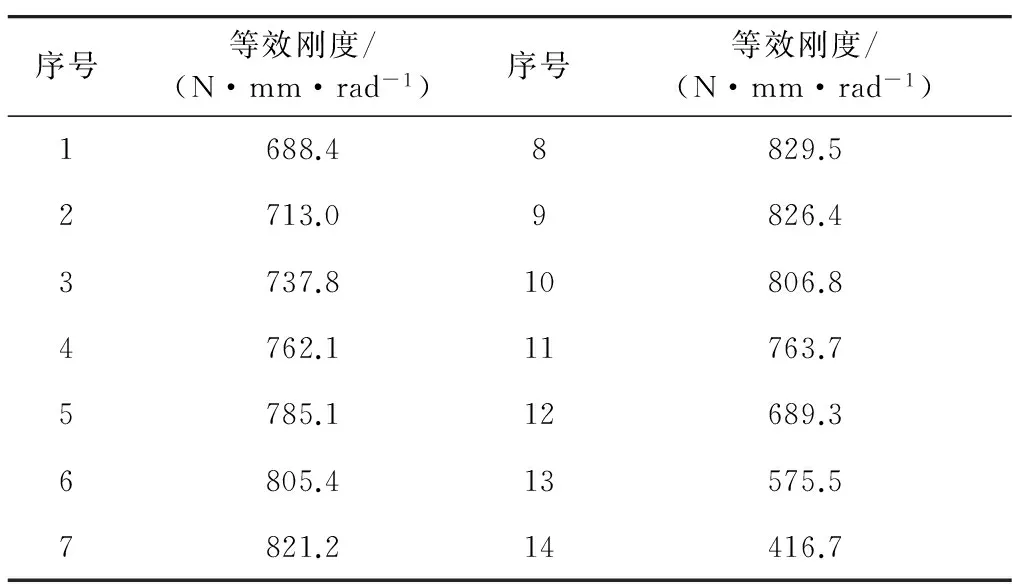
3 X形柔性铰链结构特性研究



4 结 论

