电导率连续变化大地电磁无网格法数值模拟*

黄廷哲，嵇艳鞠，2†，黄婉玉，关珊珊，姜曜

(1.吉林大学 仪器科学与电气工程学院，吉林 长春 130026；2.地球信息探测仪器教育部重点实验室，吉林 长春 130026)

电导率连续变化大地电磁无网格法数值模拟*

黄廷哲1，嵇艳鞠1，2†，黄婉玉1，关珊珊1，姜曜1

(1.吉林大学 仪器科学与电气工程学院，吉林 长春 130026；2.地球信息探测仪器教育部重点实验室，吉林 长春 130026)

针对地下空间目标体多为电性参数连续变化且分布形态复杂等特点，结合无网格法物性参数加载方便、计算精度较高、自适应分析便利等优势，基于径向基函数构造了连续导电模型下的形函数，推导了等价线性方程组，进行了电导率连续变化的二维大地电磁数值模拟，给出了形状参数最优值.通过电导率连续变化的水平层状模型验证了算法的正确性，计算结果均方根相对误差不超过0.36%，精度优于有限元法.讨论了电导率连续变化的水平模型与均匀分块模型的电磁响应差异，对连续变化的地堑模型和不同倾斜角度下油藏注水模型进行了数值模拟.研究表明：连续变化模型和均匀分块模型差异明显，在实际反演解释中采用连续变化模型有利于提高反演的精度；TM模式的观测方式对于异常体的倾斜分布具有更好的分辨能力；无网格法避免了复杂的模型输入和网格的生成，更适合计算电性参数连续变化和复杂分布的异常体响应，将成为复杂电性和分布形态下电磁探测高精度数值模拟新方法.

连续变化；大地电磁；无网格法；径向基点插值

大地电磁测深法(Magnetotelluric Sounding，MT)是通过在地面观测相互正交的电场和磁场分量来研究地球内部电性结构的一种电磁探测方法，在实际探测中得到了广泛的应用[1-2].在电性参数分块均匀的前提下， Mauriello[3]采用矩形三角网格剖分、双线性插值有限元进行了数值模拟;Kerry等[4]采用非结构化网格实现了任意复杂地电模型的大地电磁自适应有限元模拟.电性参数分块均匀的模拟方式认为在单元块内电性参数是均匀分布的，但是在实际的深部地球探测中，由于地温梯度变化以及压实作用的存在，岩矿石电性参数往往是连续变化的，例如在煤田和油气探测中，含煤岩层和饱和油藏的岩石物理学参数就表现出了连续变化的性质[5]，分块均匀模型只是连续变化模型的特殊表现形式，采用电性参数连续变化的剖分方式更符合电磁勘探的实际情况.另外，某些初步反演方法得到的电性参数也是连续变化的，连续导电模型的正演可为此类模型的反演打下基础，因此有必要对电导率连续变化的模型进行数值模拟.刘云等[6]对连续变化的模型进行了正演计算，但都是采用将电性参数赋予单元节点上的有限元方法，在子单元内电性参数采用插值构造，并未真正反映真实的电导率连续变化的情况.

无网格方法是伴随着工程计算领域的深入发展应运而生的一种新兴数值计算方法，其近似函数仅建立在一系列离散节点上，克服了传统方法对于网格的依赖，解决了动态断裂力学、金属体积成形等常规方法难以模拟的问题[7-8].在计算电磁学领域,Cingoski等[9]首次将无单元Galerkin法(Element-Free Galerkin method,EFGM)应用于电磁学计算中，成功解决了电压互感器问题.Ho等[10]总结了无网格法在计算电磁学中取得的初步成果.冯德山等[11]研究了无单元Galerkin法的二维探地雷达正演模拟，结果表明在相同的节点条件下EFGM比矩形剖分的有限单元法精度要高.李俊杰等[12]研究了大地电磁中无网格与有限元的耦合算法.目前无网格法主要用于电导率分块均匀模型的电磁数值模拟[13]，而且形函数大多数采用移动最小二乘法构造，导致本质边界条件的加载较为困难，对于实际勘探中广泛存在的电性参数连续变化的情况还未见到有相关成果发表.

本文提出用无网格径向基点插值法(Radial Point Interpolation Method,RPIM)模拟电导率连续变化的大地电磁模型，推导了对应等价线性方程组，将物性参数的加载在一个个离散的点上，较好地模拟了复杂异常体的形状和电性参数.基于Matlab软件平台编制了相应程序并计算了典型的电导率连续变化模型，结果表明无网格法能够有效地计算复杂模型下的电磁场响应，视电阻率和相位的断面图均较好地反映了电性参数连续变化的趋势，同时无网格法具有高精度计算和自适应分析便利的特点，有望成为复杂媒质和复杂构造下的电磁法数值模拟一种新的强有力方法.

1 无网格法正演理论

1.1 连续导电媒质形函数的构造

多项式基函数插值法被广泛运用于各类数值方法中，为了避免传统的多项式基函数插值所引起的奇异性，针对地下空间的连续导电媒质问题，采用径向基函数(RBF)构造无网格法形函数.由于无网格法不依赖于预定义的单元构造形函数，因此引入了支持域的概念，支持域一般为矩形或者圆形，以计算点为中心，如图1所示.

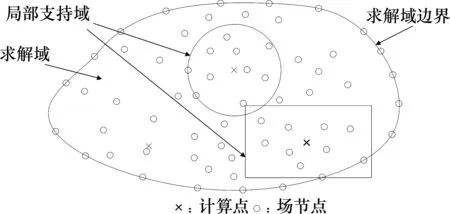
图1 无网格法节点离散示意图Fig.1 Nodes discrete sketch of meshfree method

在求解域Ω内，任意一节点XT=(x,y)的场变量u(X)在局部支持域Ωs的径向基点插值表达式为[14]：

Us=R0a+Pmb

(1)

节点场值向量Us为:

Us={u1u2…un}T

(2)

RBF的力矩矩阵为:

(3)

多项式力矩矩阵为:

(4)

式中:n为RBF的个数;m为多项式基函数的个数；ai和bj为待定常数.Ri(rk)中的rk的表达式为:

(5)

本文选用的RBF为复合2次(MQ)函数，多项式基函数的个数为3，MQ函数其表达式为：

(6)

其中αc和q为形状参数；ri是计算点与节点之间的距离.

然而式(1)中有(n+m)个变量，添加m个约束条件：

(7)

联立式(1)和式(7)可得到如下矩阵方程：

(8)

求解式(8)可得到：

(9)

可将式(9)重写为：

u(x) =RT(x)a+PT(x)b=

(10)

式中的RPIM形函数可表示为：

{φ1(x)φ2(x)…φn(x)φn+1(x)…φn+m(x)}

(11)

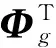
1.2 MT边值问题无网格法离散

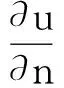
(12)

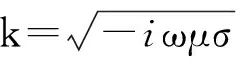
图2 二维大地电磁模拟示意图Fig.2 Sketch map of 2D MT simulation

大地电磁两种极化模式分别如下：

(13)

对于TE模式，计算区域包含空气层；对于TM模式，研究区域为地下空间，上边界AB在地面上.求取泛函F(u)对场量u的偏导数，将u(x)=ΦT(x)U带入，令泛函F(u)对场量u的偏导数为0，从而得到如下矩阵表达式：

Ku=b

(14)

式中：u={u1u2… un}T；b=[0 0 … 0]；

K=K1-K2+K3=

∫ΩλΦiΦjdΩ+∫CDτkΦiΦjdΩ

为了方便数值积分，将求解域Ω划分为若干积分单元，在求解域内和边界积分均采用高斯积分实现.上边界AB是本质边界，其场值始终是1个单位，为了加载本质边界，将系数矩阵K的对角线元素修正为αKii，对应的右端项b修正为αKii.其中α是一较大的数，这样使系数矩阵只在两处发生了变化，本质边界条件处理较为简单.

Krylov子空间方法被认为是一种有效的求解大型稀疏线性方程组方法[16].基于Krylov子空间的迭代方法收敛速度快，求解精度高，而且稳定性好.Krylov子空间方法常常与预处理技术结合求解线性方程组，本文采用有容许误差的不完全LU分解作为预条件子和稳定双共轭梯度法(BICGSTAB)进行求解，容许误差为1×10-10，最大迭代次数为1 000次，对方程组(14)求解即可得到各个节点处的场值.

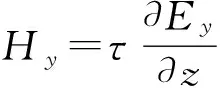
(15)

式中：h是垂直方向上等间距两个节点的距离.

得到辅助场值之后，可以通过式(16)计算视电阻率和相位：

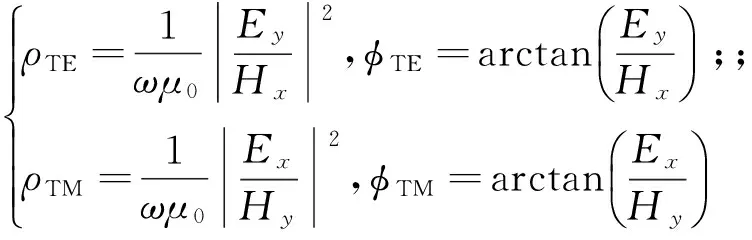
(16)

2 模型计算及分析

2.1 RPIM最优形状参数选取

径向基点插值无网格法采用RBF构造形函数，RBF中的形状参数对计算精度有直接影响，其最优值需要通过数值试验获得[17].建立ρ=100 Ω·m的均匀半空间模型，表1分别为不同支持域无量纲尺寸α，不同高斯点个数n，不同q值，以及不同αc下的视电阻率计算结果.选取计算频率为1 Hz，计算机硬件平台为CPU Intel core i7-4770 3.40 GHz，RAM 8 GB，软件编程平台为MATLAB 2015a.

由表1可以看出，支持域无量纲尺寸对于计算结果有较大影响，α的最优值介于1.1～1.6之间.高斯点个数n越大，计算结果越精确，但耗时增加较多，4点高斯即可满足精度要求.MQ函数中的形状参数q和αc具有较好的普适性，αc的取值范围约在[-45,45]之间，q的取值范围约为[-2.3,0.9]，在此范围内计算结果均保持较高的计算精度，超出此范围形函数的构造将出现奇异性.综合以上分析，本文选取的形状参数如下：支持域无量纲尺寸α为1.1，高斯点数量为4个，q=0.5，αc=1.

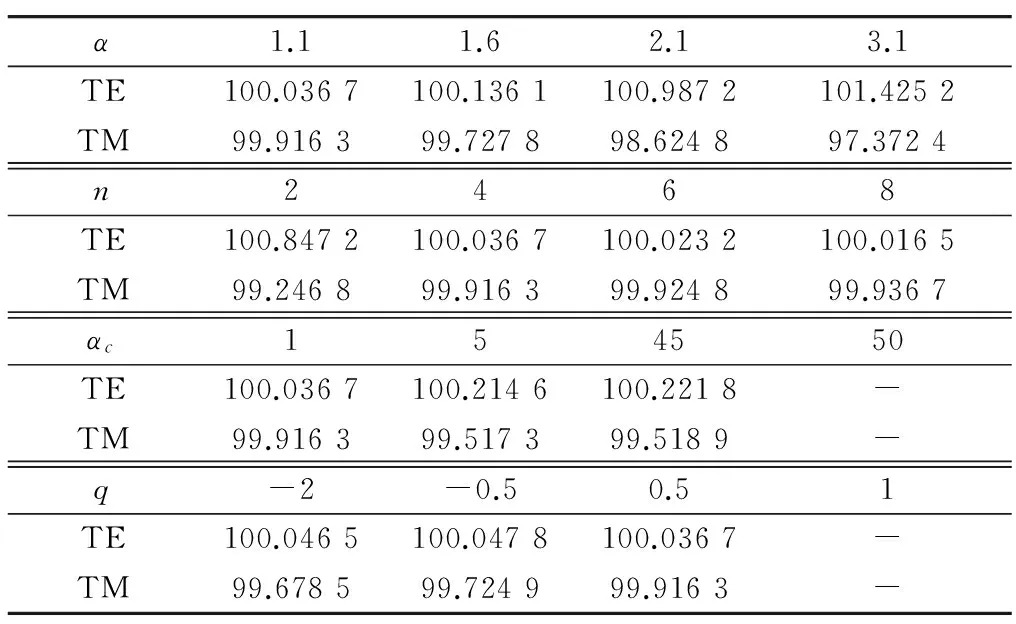
表1 不同形状参数下的视电阻率计算结果Tab.1 Apparent resistivity calculation results under different shape parameters

2.2 连续变化算法验证

建立如图3所示的水平层状模型,求解域横向规模为20 km，纵向规模为30 km.第1层及第3层电阻率是均匀的，第1层电阻率为100 Ω·m，厚度为2 km，底层电阻率为200 Ω·m.中间层含有一个电导率连续变化的水平层，其电阻率值随着深度线性增大，深度为4 km.节点均匀分布于求解域内，一共201×301个节点，节点间距100 m.背景网格的顶点和节点重合.

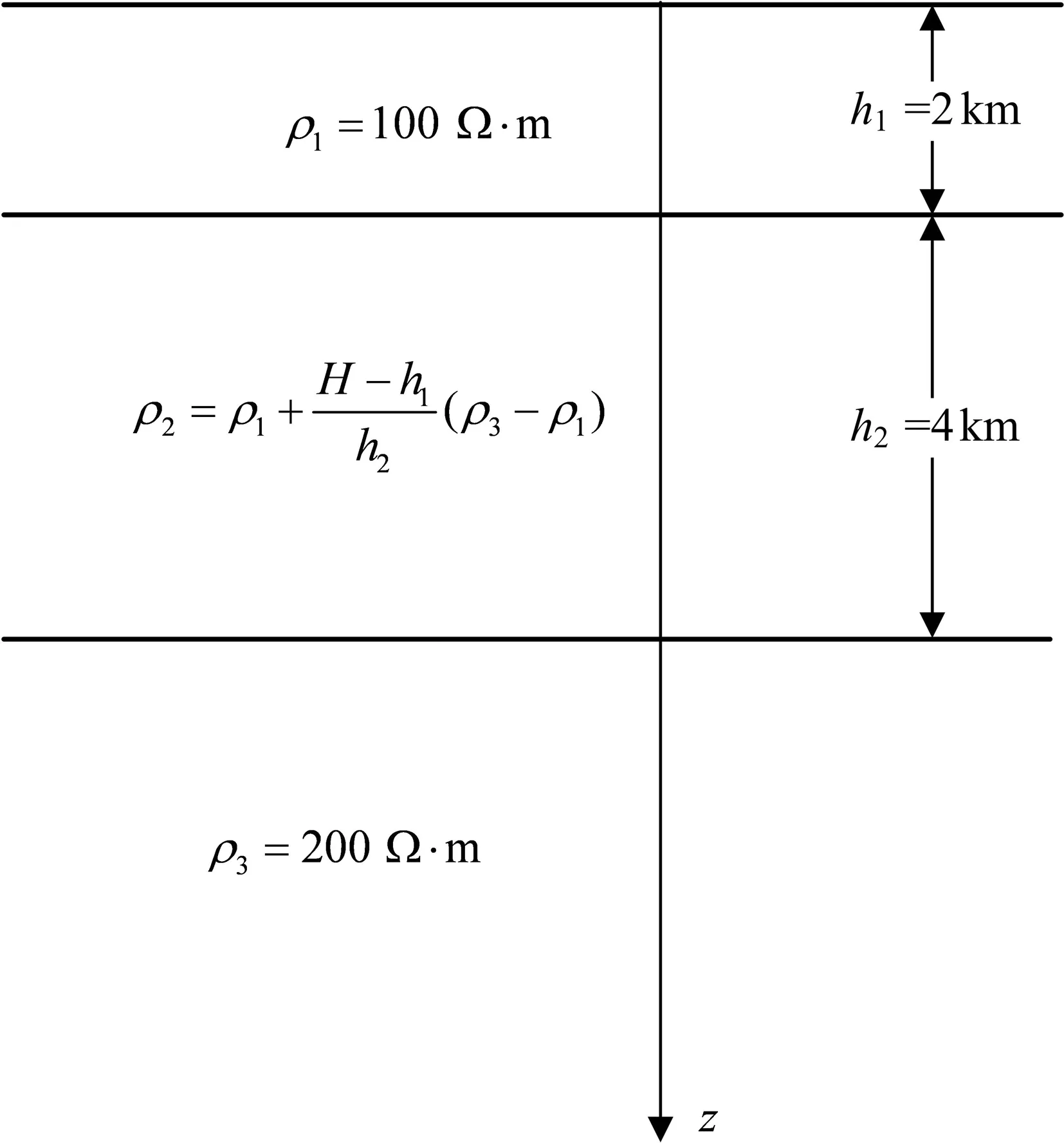
图3 电导率连续变化层状模型Fig.3 Continuous conductivity layered model

为了验证算法的正确性，将图3所示的连续导电媒质层分为19层按照层状模型求出解析解，在相同的节点分布下取地面中心点的测点为研究对象，将无网格法数值解与解析解、有限元法数值解进行对比,视电阻率和阻抗相位结果如表2和表3所示.

从表中可以看出，无网格法的数值解与解析解、有限元数值解结果高度一致，其中无网格法视电阻率和阻抗相位与解析解的均方根相对误差不超过0.36%，而有限元法均方根相对误差不超过0.74%，体现了无网格法高精度计算的特点.由于此处无网格法采用了均匀节点分布，在高频时趋肤深度较浅，因此导致在高频时计算精度略低于有限元法，计算时间约为有限元法的10倍左右，但无网格法的物性参数加载在离散的点上，避免了复杂的模型输入文件和网格的生成，计算结果的均方根相对误差更小，表明无网格法可以有效地进行较高精度下的连续导电媒质模型下大地电磁响应计算.

2.3 连续变化模型和均匀分块模型对比

为了说明连续变化模型分析的必要性，将图3所示的连续变化层的电导率取平均，并和原来的模型进行对比分析.第1层和第3层电阻率与图3相同，中间层电阻率取为图3电阻率的平均值，厚度仍为4 km，其余参数均不变.连续导电媒质模型与一维层状模型的地面中心点处的视电阻率和相位对比结果如图4所示.从图中可以看出，两者形态基本一致，但在一些频点上差异较大，其中视电阻率的最大差异可达9.8%，相位的最大差异可达7.6%，这表明连续变化模型和均匀分块模型的电磁响应差异较为明显，如果实际地电模型的电导率为连续变化，而依然采用传统的分块均匀模型进行解释，将会造成较大的偏差.

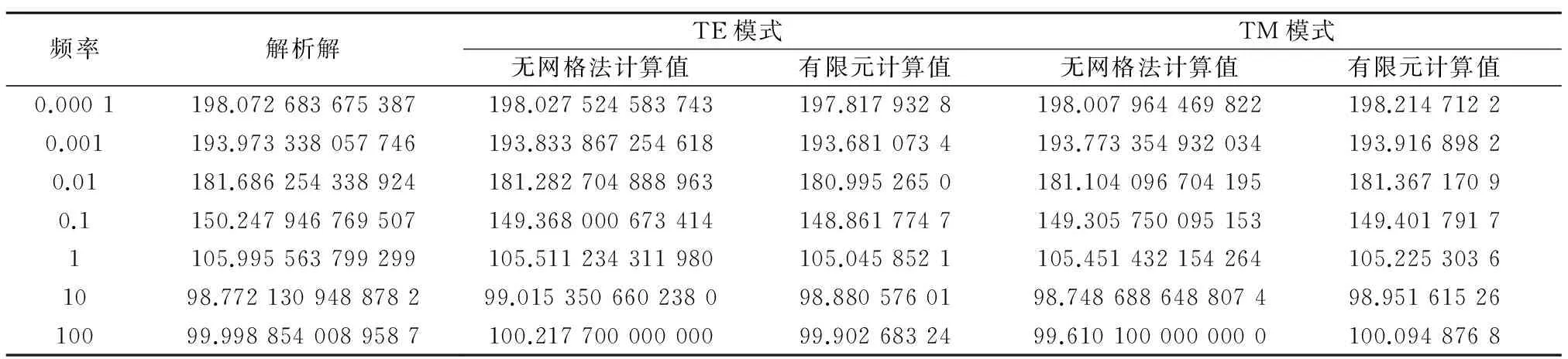
表2 视电阻率数值解和解析解对比Tab.2 Comparison of apparent resistivity between numerical solution and analytical solution

表3 相位数值解和解析解对比Tab.3 Comparison of phase between numerical solution and analytical solution

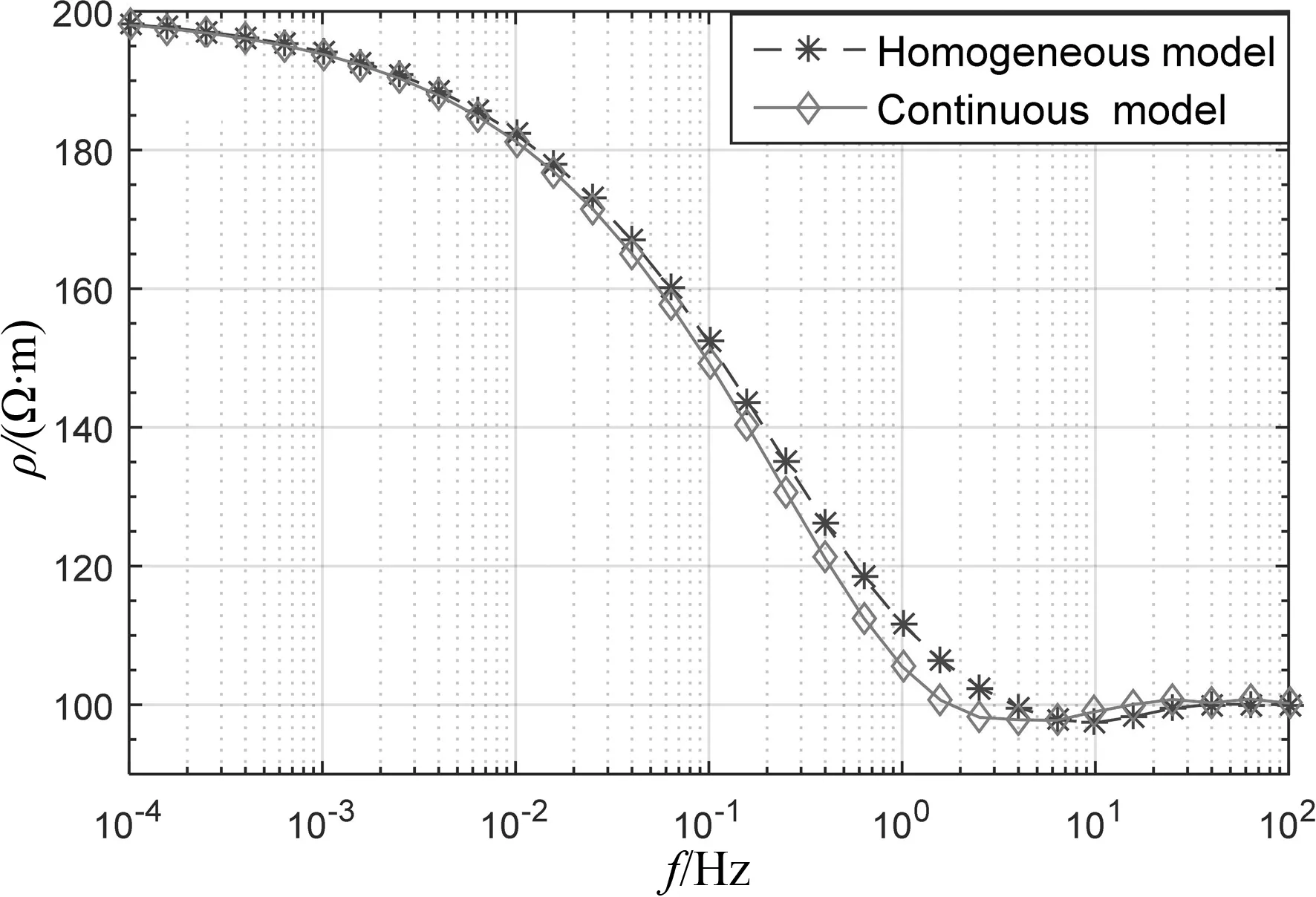
(a)视电阻率

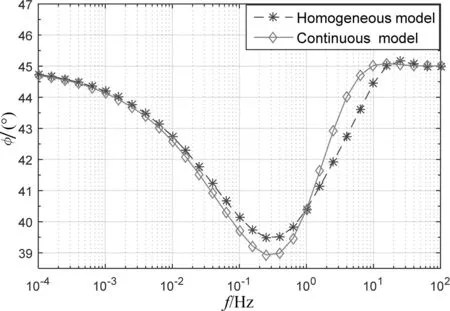
(b)相位图4 连续变化模型与分块均匀模型结果对比Fig.4 Comparison between continuous medium model and homogeneous model

2.4 连续变化地堑模型计算

分别建立如图5所示的地堑连续变化模型，第1层电阻率10 Ω·m，厚度为2 km，中间1层为过渡层，其电阻率随深度线性增大，第2层电阻率的变化为:

(17)

式中：ρ1为第1层电阻率；ρ3为第3层电阻率；H为当前的层厚度；h1,h2分别为第1层和第2层的层厚.在地堑存在的区域，h2为4 km，其他区域h2为2 km.第3层为均匀媒质层，电阻率为100 Ω·m.

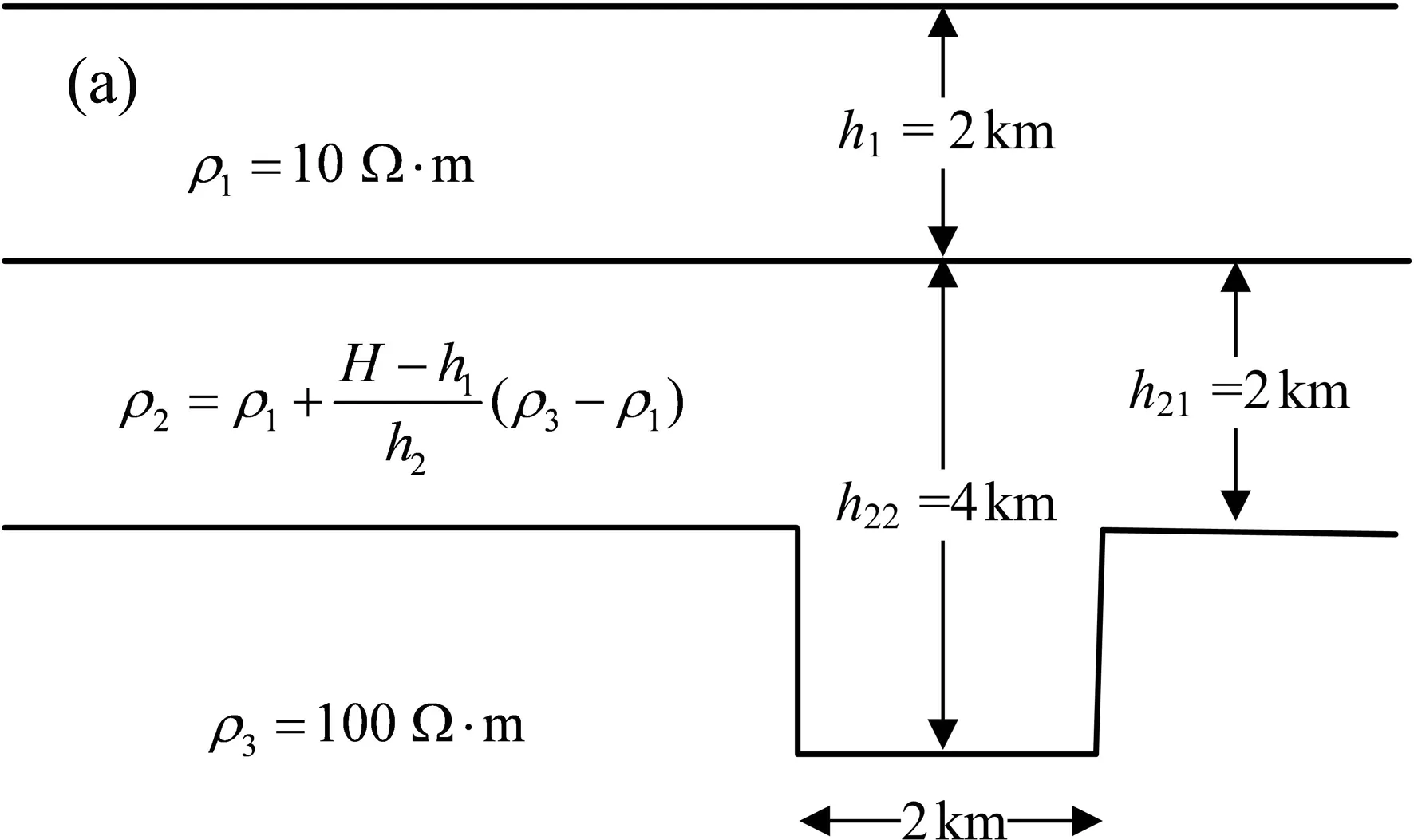
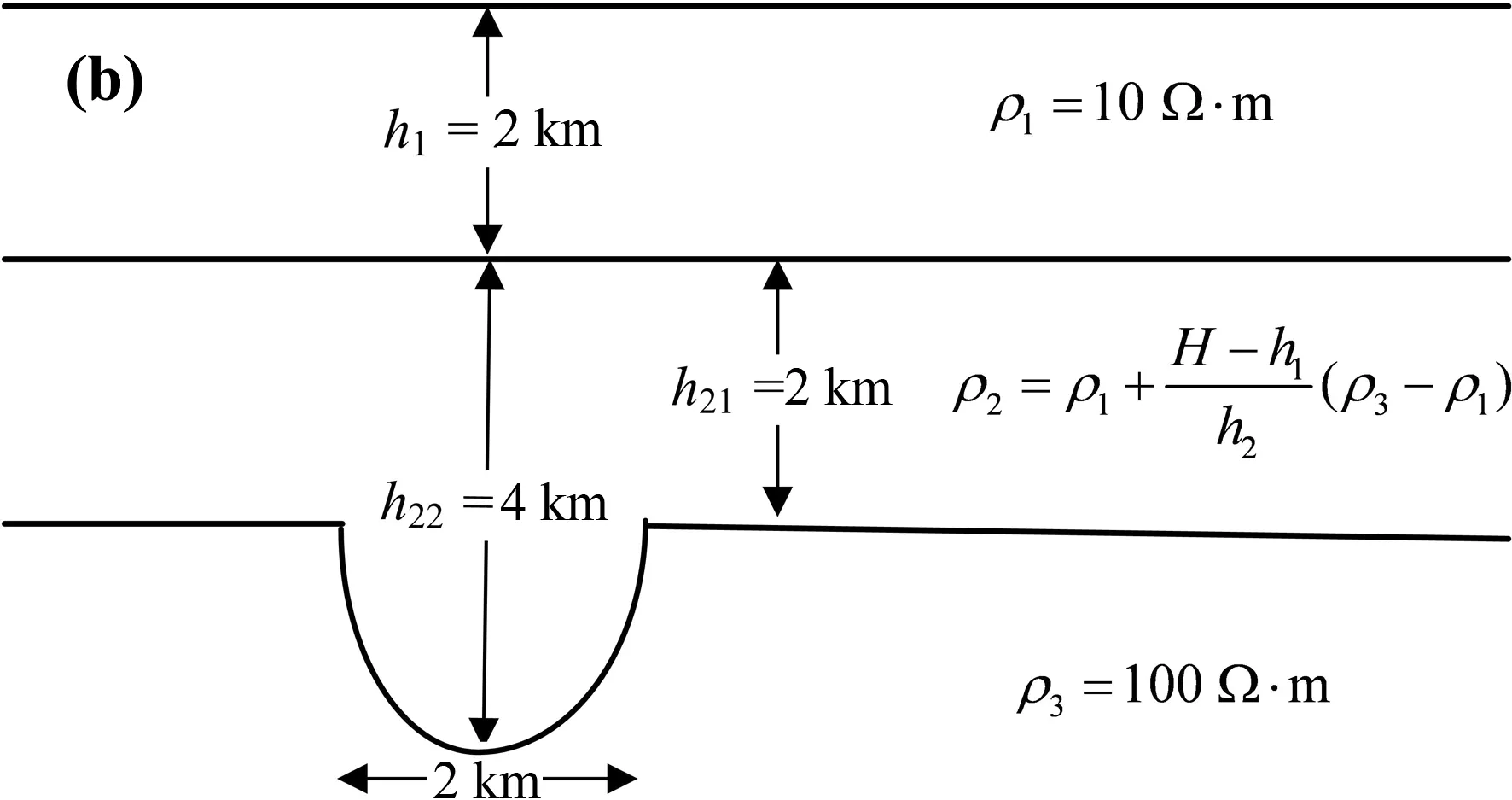
图5 地堑连续变化模型Fig.5 Continuous conductivity graben model

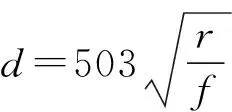
(a)视电阻率

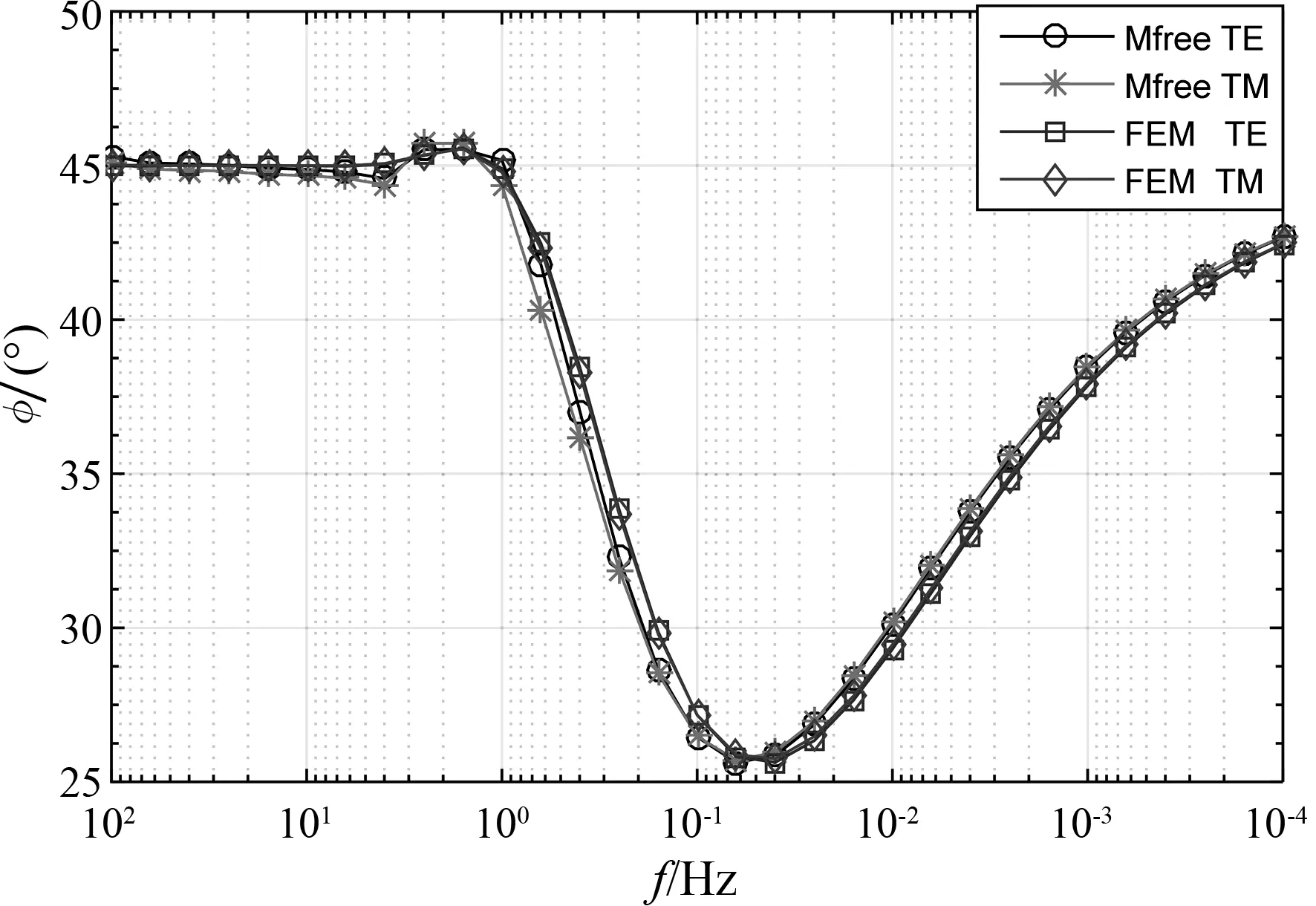
(b)相位图6 模型5(a)地面中心点测深曲线Fig.6 Ground center point sounding curve of model 5(a)

图5(b)模型的地下连续导电媒质交界面为起伏变化，用传统的方法已较难模拟.自适应有限元方法虽然可以对该模型进行模拟，但该方法需要经过多次迭代及误差估计，提高局部精度的同时却降低了整体的收敛速度，而无网格法脱离了网格的限制，只需离散的点便可构造形函数，可以非常方便地对该模型进行模拟.图7为图5(b)模型的无网格法视电阻率计算结果.

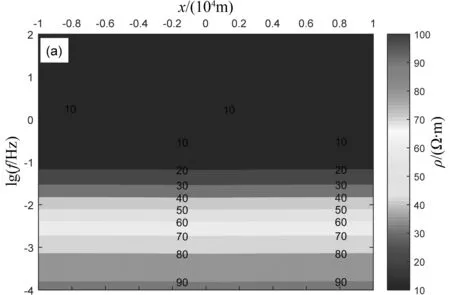
(a)TE模式

(b)TM模式图7 模型5(b)视电阻率模拟结果Fig.7 Resistivity simulation results of model 5(b)

从模拟结果中可以看出，起伏地形在视电阻率拟断面图较为明显，较为清晰地反映出了所设计模型电阻率连续变化的趋势.由于切向电场的连续性，TM模式更加清晰地反映了媒质交界处的起伏地形情况.模拟结果符合TE模式垂向分辨率较高，而TM模式横向分辨率较高的特点.

2.5 实际油藏注水模型计算

在石油地球物理勘探中，由于受到含油饱和度、含油高度、孔隙结构以及油水密度差等因素影响，油藏的电导率往往表现出连续变化的趋势.为了模拟实际中的电导率连续变化模型以及进一步突出无网格法计算复杂模型便利的优势，建立如图8所示的饱和油藏区注水模型，注水区呈椭圆形分布，电导率分布函数为：

σ(x,z)=σ0+Aexp(-(0.000 1x2+

0.000 01(z-1 500)2))

(18)

其中背景电导率为0.01 S·m，A=0.99.为了研究不同倾斜角度下的大地电磁响应，分别对注水区椭圆异常旋转0°，30°，60°和90°，不同旋转角度下的电阻率分布情况如图8所示.

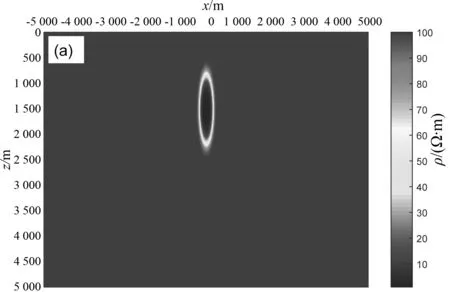
(a)旋转0°

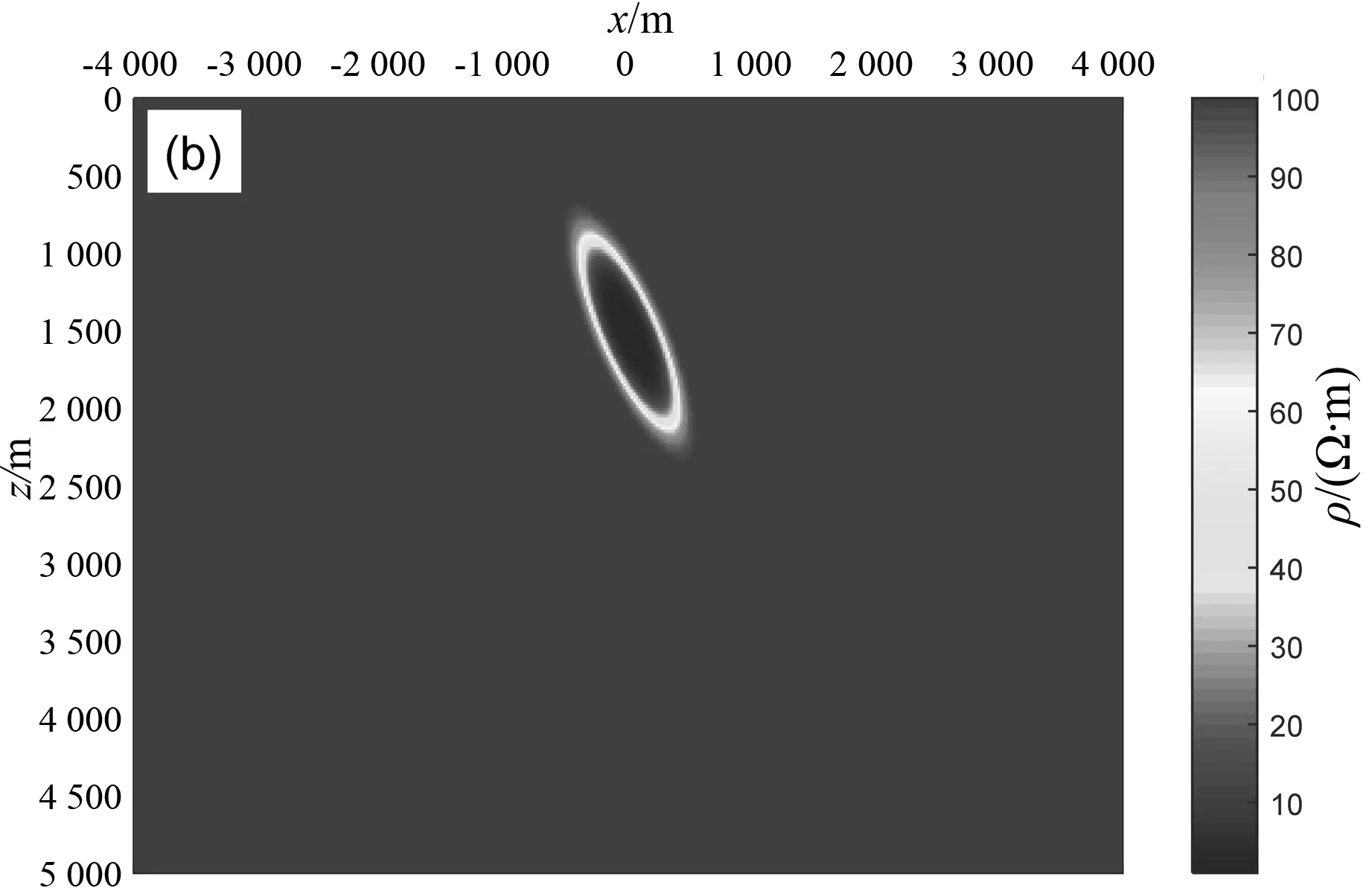
(b) 旋转30°

(c)旋转60°

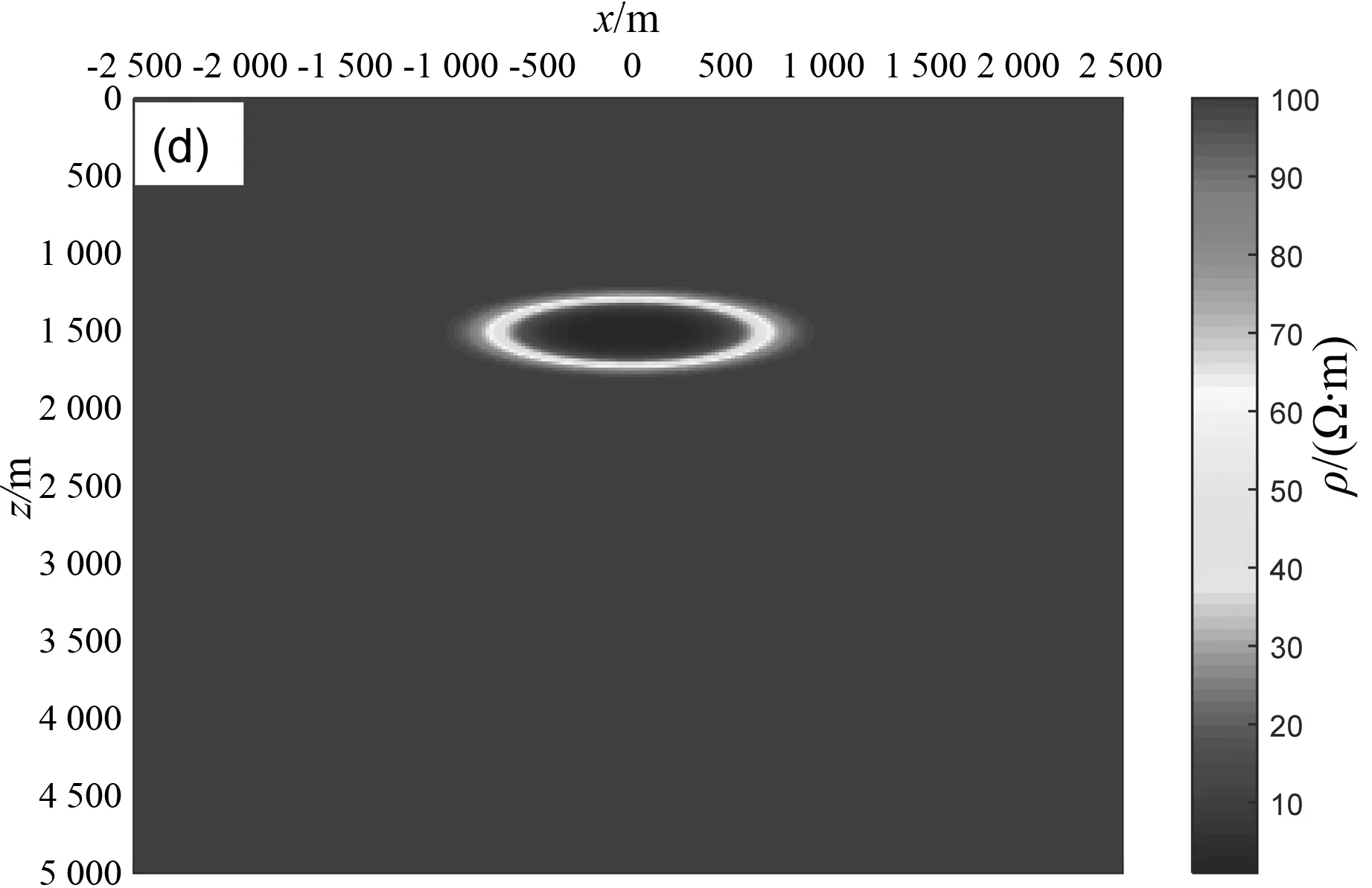
(d) 旋转90°图8 饱和油藏注水区模型Fig.8 Saturated reservoir water flooding model

该模型油藏注水区呈椭圆形，并且电导率呈非线性分布，采用传统的有限元方法已较难模拟.但无网格法不需要利用预定义的网格信息，可以方便地对该模型进行异常体形状的模拟及电性参数的加载.采用和图5相同的无网格参数，纵向采用非均匀节点分布，为了突出显示连续导电媒质模型的响应，分别计算相同旋转角度下的分块均匀模型的视电阻率，并与连续导电媒质模型下的响应相除，图9为在1 Hz频率下的视电阻率剖面曲线.

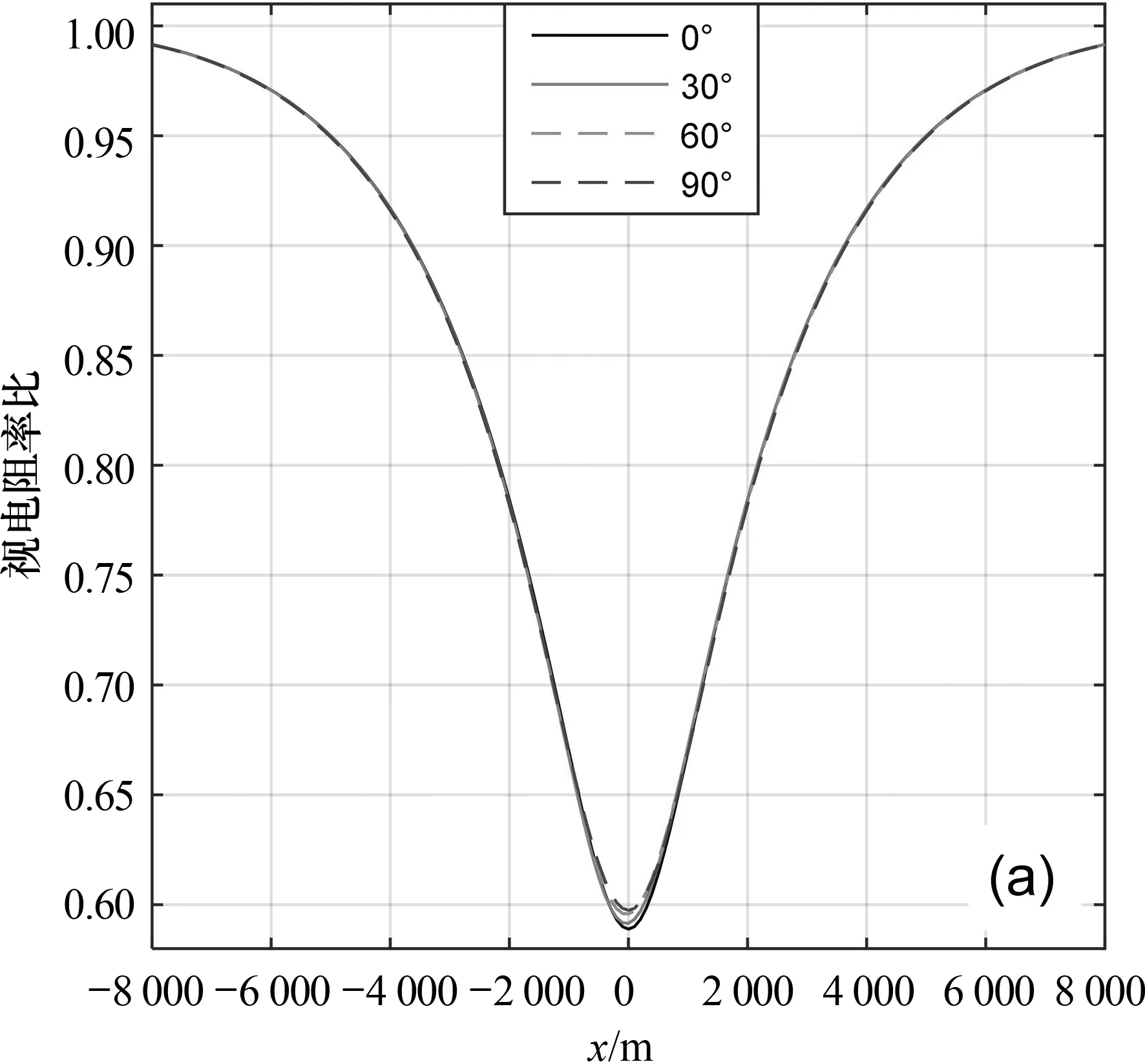
(a)TE模式

(b)TM模式图9 不同倾斜角度下的视电阻率剖面曲线Fig.9 Apparent resistivity curves under different inclination angle

从图9中可以看出，TE模式对异常体的倾向不敏感，在不同倾斜角度下的视电阻率剖面曲线几乎重合，而TM模式对异常体的倾向较为敏感，在旋转角度为0°和90°时呈现了较好的对称性，对不同的倾斜角度具备了一定的分辨能力.这是由于在TM模式下，磁场分量平行于走向，存在着与构造走向垂直的电场分量，非均匀媒质接触面在电场的作用下充电而产生了多余的附加电荷，导致TM极化模式受异常体的影响较为明显.在TE极化模式中，电场分量仅仅沿走向方向，不存在与走向垂直的电场，在不均匀媒质交界面不产生电荷积累，因此TE模式对不同倾斜角度下的不均匀体几乎表现不出分辨能力.

3 结 论

本文针对野外探测中广泛存在的电性参数连续变化的实际情况以及实际反演的需要，提出将无网格法应用到电磁法数值模拟中，基于径向基函数构造了连续导电模型下的形函数，推导了等价线性方程组，进行了电导率连续变化的二维大地电磁数值模拟，通过数值试验给出了RPIM形状参数最优值.主要结论如下：

1)电导率连续变化水平模型的无网格法计算结果均方根相对误差不超过0.36%，算法精度优于有限元法.连续变化模型和均匀分块模型差异明显，其中视电阻率的最大差异可达9.8%，在实际反演解释中采用连续导电媒质模型有利于提高反演的精度.TM极化模式对于异常体的倾斜状况更加敏感.

2)基于径向基函数的无网格法形函数构造脱离了网格的限制，本质边界条件加载非常容易，计算精度相对较高，物性参数的加载在一个个离散的计算点上，可通过形状参数来调整支持域的大小，以实现在模型的特征区精细化模拟，特别适合连续变化等复杂形态地质构造的计算，自适应分析便利，具有较强的实用性，将成为复杂电性和分布形态下电磁探测高精度数值模拟新方法.

3)相比于分块均匀的正演模拟，许多有效的反演方法(如 Bostick，Occam 等 )都是假设地下导电媒质是连续的，而无网格法为连续模型正演计算提供了新的思路，在电磁探测领域将具备广阔的应用前景.

致谢：吉林大学李桐林教授，陈汉波博士及中国海洋大学卢杰博士、潘林冬硕士对本文的研究和写作提供了指导和帮助，审稿专家对本文提出了宝贵意见和建议，在此表示衷心的感谢.

[1] 顾观文,吴文鹂,李桐林.大地电磁场三维地形影响的矢量有限元数值模拟[J].吉林大学学报:地球科学版,2014,44(5):1678-1686.

GU Guanwen,WU Wenli,LI Tonglin.Modeling for the effect of magnetotelluric 3D topography based on the vector finite-element method[J].Journal of Jilin University:Earth Science Edition，2014,44(5):1678-1686.(In Chinese)

[2] 汤井田，李晋，肖晓,等.基于数学形态滤波的大地电磁强干扰分离方法[J].中南大学学报:自然科学版，2012,43(6):2215-2221.

TANG Jintian,LI Jin,XIAO Xiao,etal.Magnetotelluric sounding data strong interference separation method based on mathematical morphology filtering[J].Journal of Central South University:Science and Technology,2012,43(6):2215-2221.(In Chinese)

[3] MAURIELLO P,PATELLA D.Principles of probability tomography for natural-source electromagnetic induction fields[J].Geophysics，1999,64(5):1403-1417.

[4] KERRY K,CHESTER W.Adaptive finite-element modeling using unstructuredgrids:The 2D maggnetotelluric example[J].Geophysics，2006,71(6):291-299.

[5] ГРЕЧУХИН В В著，蔡柏林等译.应用地球物理方法研究含煤建造[M].北京:地质出版社,1987:51-60.

ГРЕЧУХИН В В.Translated by CAI Bailin，etal.Application of geophysical methods studying coal bearing building[M].Beijing:Geology Press，1987:51-60.(In Chinese)

[6] 刘云，王绪本.电性参数分块连续变化二维MT有限元数值模拟[J].地球物理学报，2012,55(6):2079-2086.

LIU Yun,WANG Xuben.The FEM for modeling 2-D MT with continuous variation of electric parameters within each block [J].Chinese Journal of Geophysics，2012，55(6):2079-2086.(In Chinese)

[7] 龙述尧,张国虎.基于MLPG法的动态断裂力学问题[J].湖南大学学报:自然科学版,2012,39(11):41-45.

LONG Shuyao,ZHANG Guohu.An analysis of the dynamic fracture problem by the meshless local Petrov-Galerkin method[J].Journal of Hunan University:Natural Sciences,2012,39(11):41-45.(In Chinese)

[8] 郑刚，伍素珍，李光耀，等.金属体积成形过程的无网格RPIM方法分析[J].湖南大学学报:自然科学版,2010,37(10):41-46.

ZHENG Gang,WU Suzhen ,LI Guangyao,etal.Numerical simulation of bulk forming processes by radial point interpolation method(RPIM) [J].Journal of Hunan University:Natural Sciences，2010，37(10):41-46.(In Chinese)

[9] CINGOSKI V，MIYAMOTO N，YAMASHIT A.Hybrid element-free Galerkin-finite element method for electromagnetic field computations[J].IEEE Transactions Magnetics,2000,36(4):1543-1547.

[10]HO S L，YANG S，MACHADO J M,etal.Application of a meshless method in electromagnetics[J].IEEE Transactions on Magnetics，2001,37(5):3198-3202.

[11]冯德山,王洪华,戴前伟.基于无单元Galerkin法探地雷达正演模拟[J].地球物理学报,2013，56(1):298-308.

FENG Deshan,WANG Honghua,DAI Qianwei.Forward simulation of ground penetrating radar based on the element-free Galerkin method [J].Chinese Journal of Geophysics,2013,56(1):298-308.(In Chinese)

[12]李俊杰,严家斌.大地电磁二维正演中的有限元-径向基点插值法[J].中国有色金属学报,2015,25(5):1314-1324.

LI Junjie,YAN Jiabing.Magnetotelluric two-dimensional forward by finite element-radial point interpolation method[J].The Chinese Journal of Nonferrous Metals,2015，25(5):1314-1324.(In Chinese)

[13]嵇艳鞠,黄廷哲,黄婉玉,等.起伏地形下各向异性的2D大地电磁无网格法数值模拟[J].地球物理学报,2016,59(12):4483-4493.

JI Yanju,HUANG Tingzhe,HUANG Wanyu,etal.2D anisotropic magnetotelluric numerical simulation using meshfree method under undulating terrain[J].Chinese Journal of Geophysics,2016,59(12):4483-4493.(In Chinese)

[14]LIU G R,GU Y T著.王建明，周学军译.无网格法理论及程序设计[M].济南：山东大学出版社，2007:45-48.

LIU G R,GU Y T.Translated by WANG Jianming,ZHOU Xuejun.An introduction to meshfree methods and their programming [M].Jinan:Shandong University Press,2007:45-48.(In Chinese)

[15]徐世浙.地球物理中的有限单元法[M].北京:科学出版社，1994:229-239.

XU Shizhe.Finite element method in geophysics[M].Beijing:Science Press,1994:229-239.(In Chinese)

[16]柳建新，蒋鹏飞，童孝忠,等.不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用[J].中南大学学报:自然科学版,2009,40(2):484-491.

LIU Jianxin,JIANG Pengfei,TONG Xiaozhong,etal.Application of BICGSTAB algorithm with incomplete LU decomposition preconditioning in two-dimensional magnetotelluric forward modeling[J].Journal of Central South University:Science and Technology,2009,40(2):484-491.(In Chinese)

[17]李俊杰，严家斌.RPIM求解点源二维变分问题的最优形状参数[J].物探与化探,2015,39(6):1233-1237.

LI Junjie,YAN Jiabing.Optimal shape parameters of RPIM for resolving point source two-dimensional variational problem [J].Geophysical and Geochemical Exploration,2015,39(6):1233-1237.(In Chinese)

Magnetotellurics Simulation with Continuous Variation of Conductivity Based on Meshfree Method

HUANG Tingzhe1，JI Yanju1 2†，HUANG Wanyu1，GUAN Shanshan1，JIANG Yao1

(1.College of Instrumentation and Electrical Engineering，Jilin University，Changchun 130026，China；2.Key Laboratory of Geo-Exploration Instrumentation，Ministry of Education，Jilin University，Changchun 130026，China)

In view of the problem in which most target bodies are continuously changing and the distribution is complex in the actual geological structures,2-D magnetotelluric forward modeling is simulated combined with the advantage of meshfree method where parameter loading is convenient,calculation accuracy is high and adaptive analysis is convenient.The shape function of the continuous medium model is constructed by the radial basis function,the equivalent linear equations are derived and the corresponding program is compiled.The optimal values of the shape parameters are given by numerical experiments.The correctness of meshfree method is verified by a horizontal continuous variation layered model.The root mean square error of the calculation results is not more than 0.36%,and its accuracy is superior to the finite element method.The electromagnetic response of the horizontal layer with the continuous variation of electrical conductivity and the uniform block model is discussed,and a graben terrain model and a reservoir water flooding model whose conductivity is continuously variable are calculated,respectively.The conclusions are given: the electromagnetic responses between the continuous variation model and uniform block model are significantly different,the use of the continuous variation model is helpful to improve the accuracy of inversion in the actual interpretation,and the observation method of the TM mode has better resolution for the inclination distribution of anomalous body.The meshfree method does not need the complicated mesh generation,and it is more suitable to calculate the response of continuous variation and complex distribution models.Therefore,meshfree method is expected to be a new and robust method for the numerical simulation of complex medium and complex structures.

continuous variation；magnetotelluric；meshfree method；radial point interpolation

1674-2474(2017)08-0091-09

10.16339/j.cnki.hdxbzkb.2017.08.014

2016-12-11

国家自然科学基金资助项目(41674109),National Natural Science Foundation of China(41674109);国家重大科研装备研制资助项目(ZDYZ2012-1-05),National Major Scientific Research and Equipment Development Project(ZDYZ2012-1-05)

黄廷哲(1988-)男，河南南阳人，吉林大学博士研究生

†通讯联系人：E-mail:jiyj@jlu.edu.cn

TM153

A