低功耗双带隙结构的CMOS带隙基准源*

肖璟博，陈敏，张成彬，刘云超，陈杰†

(1.中国科学院微电子研究所，北京 100029；2.中国科学院大学，北京 100049)

低功耗双带隙结构的CMOS带隙基准源*

肖璟博1,2，陈敏1，张成彬1，刘云超1，陈杰1†

(1.中国科学院微电子研究所，北京 100029；2.中国科学院大学，北京 100049)

随着片上系统的发展，带隙基准源精度和功耗的要求也越来越高.目前的高阶温度补偿方法在工艺兼容、设计复杂度和功耗上还存在一定的局限性.本文推导了一个新颖的电流模带隙基准电路在饱和区工作时的温度特性，并结合双带隙结构在输出支路上采用电流比例相减的方式实现有效的曲率补偿，从而实现了一个新颖的双带隙结构CMOS带隙基准源.在GSMC 0.18 μm工艺下，设计的CMOS带隙基准源版图面积为0.066 mm2.蒙特卡罗后仿真的结果表明，在-40～125 ℃温度范围内平均温度系数为14.27 ppm/℃；在27 ℃时基准电压平均值为1.201 V，标准偏差变化仅为33.813 mV(2.82%)；在3.3 V工作电压下，静态电流平均为9.865 μA，电源抑制为-37.21 dB.本文设计的带隙基准源具有高精度、低功耗、结构简单的特点，是片上系统的良好选择.

带隙基准电压源；曲率补偿；温度系数；低功耗

带隙基准源可以产生带有低温度系数(temperature coefficient，TC)的精确电压，在模拟集成电路和混合信号集成电路中起着非常关键的作用[1].通常的带隙基准(bandgap reference，BGR)产生消除了一阶温度系数的基准电压[2-3]，但由于双极晶体管(bipolar junction transistor，BJT)的基极和射极电压差(base-emitter voltage,VBE)存在高阶温度系数，带隙基准产生的基准电压并不能真正与温度无关.为了得到更好的温度性能，已经有大量文献对多种曲率补偿技术进行研究.例如，在文献[4-5]中，不同温度特性材料的同一器件用来提供高阶温度系数，比如不同材料的电阻和三极管.文献[6]通过BJT的电流增益产生与温度呈自然指数关系的电流，从而补偿高阶温度系数.然而，上述两种技术对工艺的变化比较敏感，也不兼容主流的互补金属氧化物半导体(complementary metal-oxide-semiconductor transistor,CMOS)工艺.文献[7]和[8]提出了VBE线性化技术，其利用BJT流过不同温度特性电流时VBE表达式的不同，通过加法或者减法来抵消高阶温度项，但是这种技术的电路结构比较复杂.文献[9-12]提出了分段线性化补偿技术，在高于或者低于设定温度值时产生非线性电流，电路结构实现较为简单，但是工艺角的变化可能会造成方法失效.文献[13-15]实现了双带隙结构的曲率补偿技术，通过两个一阶补偿的基准电流相加或者相减来补偿高阶温度系数，这种技术简单且易于实现，但是消耗的功耗较高.

综上所述，如何实现与CMOS工艺兼容、结构简单、功耗较低的曲率补偿带隙基准源是目前研究的关键问题.针对这些问题，本文在双带隙结构的曲率补偿技术基础上，提出了一种新型的基于电流比例减法的带隙基准源设计.文中引入一种在亚阈值区工作的新颖结构的带隙基准电路，推导并仿真验证其在饱和区时的温度性能与传统结构的带隙基准的温度性能存在较大差距，作为电流比例减法实现曲率补偿的依据，同时也克服了由于二阶温度系数相近导致电流相减无法合理实现的问题[13].通过在输出端实现基于电流比例减法的曲率补偿电路，得到高阶温度补偿的基准电压.此外，由于使用了电流镜自偏置结构来恒定电压，功耗得到了大大降低.

1 电流比例相减原理分析

1.1VBE的温度特性

由于BJT良好的温度特性，其通常被选为CMOS带隙基准源的主要器件.当BJT正常工作时，其VBE可表示为[1,4,6-10,12-16]

VBE(T)=VG0(Tr)-[VG0(Tr)-

(1)

式中:VG0(Tr)是在基准温度Tr时的带隙电压;ξ是集电极电流的温度阶数;η是与温度无关而与工艺有关的常量;VT为热电压.从式(1)可以看出，VG0(Tr)是常量，[VG0(Tr)-VBE(Tr)]T/Tr是一阶温度项，(η-ξ)VTln(T/Tr)是高阶温度项.因此，可通过泰勒展开将VBE表示为

VBE=a0+a1T+(a2T2+…+anTn)

(2)

式中a0，a1，…，an表示VBE各阶温度系数.

1.2 电流比例相减

通过电流比例相减实现曲率补偿的前提为用于相减的两个电流均为一阶温度补偿后的电流，分别设为I1和I2.因此将两个电流乘以相应系数进行相减时，可以抵消高阶的温度系数.由1.1节可知，VBE存在高阶温度系数，所以双带隙结构的电流比例相减，可以等效地表示为两个VBE电压的比例相减，将式(2)代入得到式(3)[13]：

K1I1-K2I2⟹K1VBE1-K2VBE2=

(K1a0_1-K2a0_2)+(K1a1_1-K2a1_2)T+

(K1a2_1-K2a2_2)T2+…+

(K1an_1-K2an_2)Tn

(3)

其中K1和K2分别为电流I1和I2的系数.一阶温度项会被补偿，故考虑相减后的二阶温度系数项.由于VBE电压的温度系数接近，即a2_1和a2_2接近，所以通过电流比例相减时，若要将二次项的系数抵消99%，即K2/K1=0.99，在I1和I2接近20 μA时，比例相减后的电流仅为I1(1-K2/K1)=0.2 μA，对于0.7 V的基准电压，需要3.5 MΩ的电阻[13].若补偿99%后，相减后的电流为8.2 μA的合理值，此时的I1和I2接近820 μA[13].若I1和I2的二阶温度系数存在M(M>1)倍的差距，则K2/K1=0.99/M时即可将二次项的系数抵消99%，此时相减之后的电流增大为I1[1-K2/(K1M)].综上所述，通过设计得到两个一阶补偿之后但二阶系数存在较大差距的电流，可以采用电流比例相减的方法在合理值范围内实现曲率补偿.

2 提出的带隙基准源设计

2.1 提出的带隙基准原理

图1是提出的带隙基准结构原理图，其包含了两个带隙基准核心电路，分别为改进传统结构的BGR core A和新颖结构的BGR core B，中间为曲率补偿电路.通过NMOS电流镜复制IREFB至输出支路，并完成比例相减，因此，输出基准电压VREF如式(4)所示

VREF=(R1+R2)IREFA-KR2IREFB

(4)

其中K为NMOS电流镜尺寸之比.IREFA和IREFB都是一阶温度补偿的电流，但有不同的高阶温度系数.若在输出端以适当的比例相减，它们的高阶项可以得到很好的抵消.

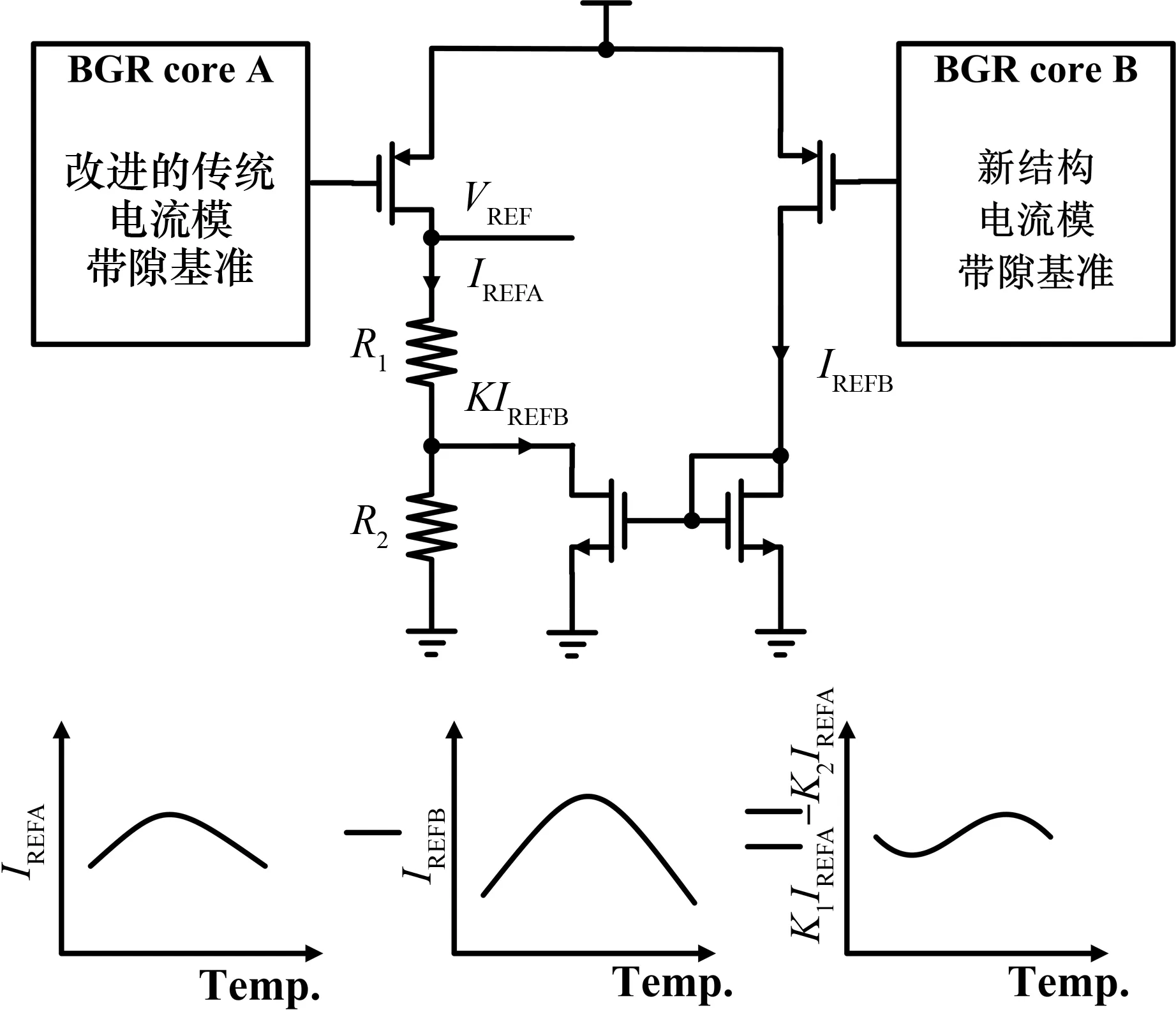
图1 提出的带隙基准结构和原理Fig.1 Proposed structure and schematic of bandgap reference

2.2 BGR core A的电路实现

传统的电流模带隙基准结构使用运放作为核心支路的恒压器件，从而得到与绝对温度成正比的(proportional to the absolute temperature ，PTAT)电流，但是运放也会消耗一定的功率.为了降低功耗，用电流镜连接方式的NMOS管代替运放实现恒定电压的功能.改进后的传统电流模带隙基准如图2中BGR core A部分所示.NM1和NM2替换运放并连接在核心支路上，节省了运放部分的功耗.PM2,PM1,NM1和NM2形成闭环环路，恒定A,B两点的电压，可以得到流经R3的电流IPTATA为:

(5)

其中N为Q2与Q1的发射结面积之比，而流经R4的与绝对温度成反比的(complementary to the abso-lute temperature ，CTAT)电流ICTATA为:

(6)

电流IPTATA和ICTATA在B点相加，并通过PM2复制至PM3，由式(5)和(6)得到IREFA的表达式为

(7)

式中VT为热电压，与温度为一阶线性关系，调节R3与R4的比例，可以得到一阶补偿的IREFA.

2.3 BGR core B的电路实现

BGR core B 的设计借鉴了新结构的电流模带隙基准[16]，如图2中BGR core B部分所示，其MOS管工作在亚阈值区，通过两个MOS管栅源电压VGS之差提供高阶温度项.与之不同的是，本文的MOS管工作在饱和区.通过本节的分析可以知道，BGR core B 仍然是一阶补偿的带隙基准.下文将详细分析IREFB的温度特性.

BGR core B的PTAT电流产生方式与BGR core A一致，则IPTATB可表示为：

(8)

其中N为Q4与Q3的发射结面积之比.CTAT电流的产生方式与BGR core A不同.NM4和NM5的栅级连接至NM6，从而在R6上产生CTAT电流.注意到

VEB3+VGS5=VGS6+ICTATBR6

(9)

其中VGS5和VGS6分别为NM5和NM6的栅源电压，因此ICTATB可表示为

(10)

IPTATB和ICTATB分别通过PM4和PM8,PM6和PM7电流镜在输出支路上相加得到IREFB，则IREFB可表示为：

(11)

对IREFB求取关于温度T的一阶偏导数，可以得到：

图2 提出的带隙基准源的晶体管级电路Fig.2 Transistor-level circuit of the proposed bandgap reference

(12)

其中k为玻尔兹曼常数，q为基本电子电荷量.当MOS管工作在饱和区时[13]，式(13)成立

(13)

其中b接近于0，VTH为MOS管的阈值电压，而对于VTH的温度特性[13]，可以表示为:

VTH≈VTH(Tr)+βTH1(T-Tr)+

βTH2(T-Tr)2

(14)

其中βTH1和βTH2分别是VTH的一阶温度系数和二阶温度系数，Tr与式(1)中的含义相同.将式(13)和(14)代入(12)，得到:

(15)

式中:βTH11和βTH21,βTH12和βTH22分别是NM5和NM6阈值电压的一阶和二阶温度系数.因此，通过调节R5和R6的比例，BGR core B也是一阶温度补偿的带隙基准.从式(15)中可以看到，相比BGR core A，BGR core B有额外的二阶温度系数2(βTH21-βTH22)/R6.由于额外二阶温度系数的存在，其一阶补偿之后的温度系数TC与BGR core A不同，避免了IREFA和IREFB因二阶温度系数接近导致相减之后电流过小的问题.

2.4 启动电路

通常情况下，带隙基准电路存在两种稳定状态.一种是零电流状态，另一种是正常工作状态.而启动电路的作用是在电路上电时，使带隙基准能够进入正常的工作状态.本文设计的启动电路如图3所示.由于PM9栅极接地，所以PM9导通，NM9流过电流，经NM9,NM10电流镜和PM10,PM11电流镜，将电流复制给PM12和NM12，因此限制了由PM12和NM12构成的反相器的最大动态电流，防止反相器在启动时有较大的电流过冲.当电路开始上电时，VREF为低电平，此时反相器输出高电平，NM7导通，拉低VSTRP的电压，而VSTRP连接至带隙核心电路中PMOS管的栅极，使得PMOS管导通，核心电路开始流过电流，脱离零电流状态.当上电完成时，反相器判定VREF为高，输出低电平，关断NM7.至此，带隙基准电路完成启动.为了防止启动电路消耗较多的功率，PM9的栅长L取得较大，所以PM9和NM9支路以及PM10和NM10支路流过的静态电流很小.

图3 带隙基准启动电路Fig.3 Start-up circuit of bandgap reference

3 仿真结果分析和对比

3.1 带隙核心电路TC仿真对比

新的带隙基准电路包含两个带隙核心电路，本节分别对两个带隙核心电路产生的IREFA和IREFB电流进行了仿真对比.图4给出了在tt工艺角下IREFA和IREFB随温度变化仿真结果.其中，IREFA的温度系数为2.175 ppm/℃，IREFB的温度系数为79.7 ppm/℃，IREFB的 TC明显大于IREFA的TC，表明在一阶补偿过后，IREFB的二阶温度系数大于IREFA的二阶温度系数，从而验证了前面的推导.

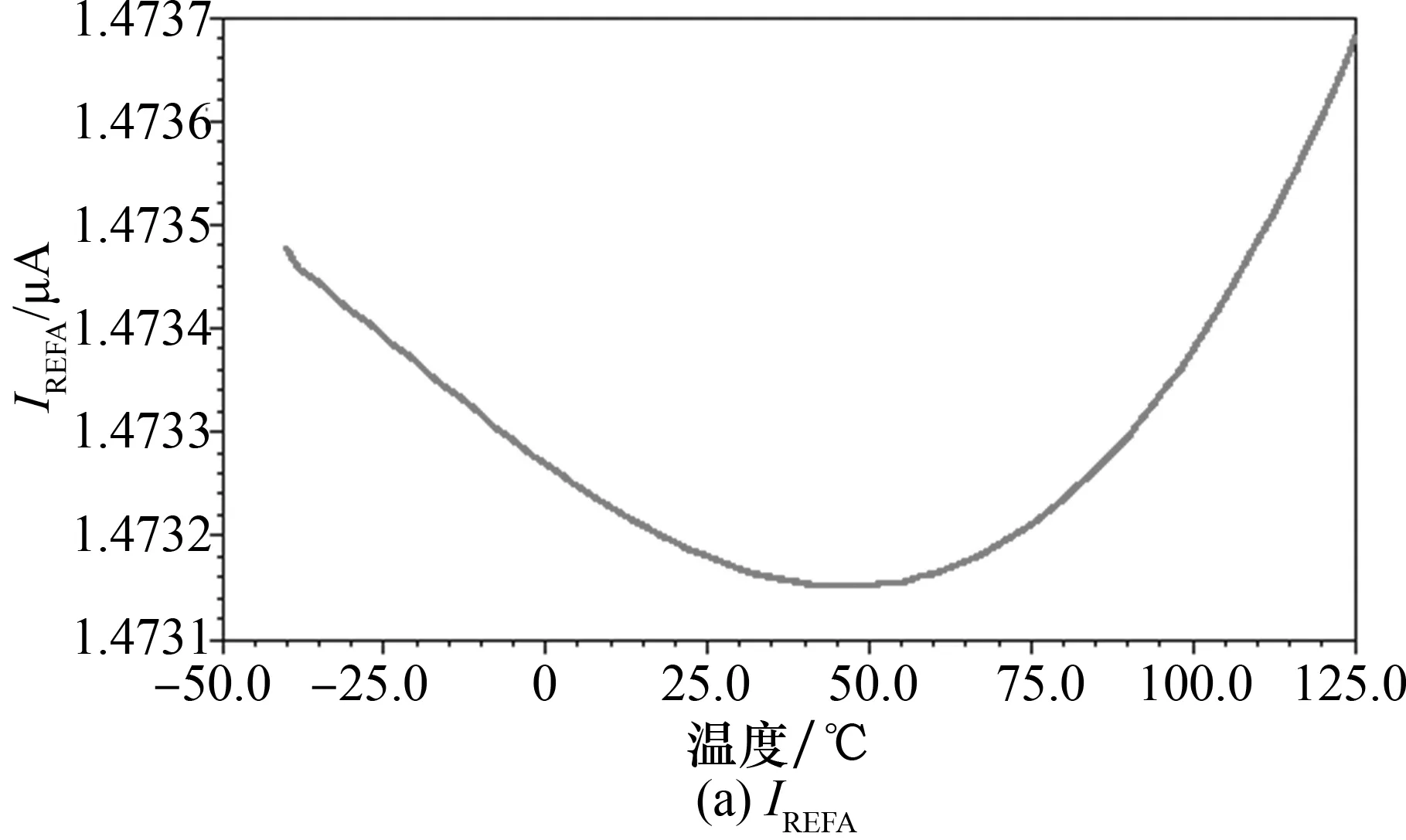
图4 温度特性曲线Fig.4 Temperature characteristic curve

3.2 带隙基准的仿真结果和对比

本文的带隙基准源在GSMC 0.18 μm工艺下设计和仿真，版图面积为0.066 mm2(175 μm×377 μm)，如图5所示.仿真采用的典型电源电压为3.3 V.图6给出了在tt工艺角下VREF基准电压的温度特性曲线，此时的温度系数为1.068 ppm/℃，温度范围为-40～125 ℃.从曲线的变化趋势可以看出，曲线呈现出曲率补偿后的温度特性，相对于一阶补偿的温度系数有了明显降低，表明提出的带隙基准电路实现了曲率补偿，并具有低的温度系数.

图5 带隙基准源版图Fig.5 Layout of bandgap reference

图6 tt工艺角下VREF基准电压的温度特性曲线Fig.6 Temperature characteristic curve of VREFreference voltage in tt corner

由于带隙基准电路对工艺制造的变化比较敏感，所以为了分析工艺变化和管子失配带来的影响，对本文设计的带隙基准进行了300次的蒙特卡罗后仿，结果如图7所示.图7(a)为VREF基准电压关于温度的特性曲线，可以看出，大部分曲线在1.2 V附近.图7(b)统计了本文设计的带隙基准在-40～125 ℃的温度性能，其中236次仿真结果的温度性能在20 ppm/℃以下，平均的温度性能为14.27 ppm/℃.图7(c)给出了在常温27 ℃时输出基准电压值的统计结果，平均输出电压为1.200 97 V，标准差为33.813 1 mV，对应变化系数为2.82%.功耗是带隙基准的重要指标之一.本文设计的带隙基准源的平均电流消耗为9.865 μA，最大的电流消耗为10.6 μA，如图7(d)所示.图7(e)给出了本文带隙基准的电源抑制(power supply rejection，PSR)性能，其低频PSR为-37.21 dB，在100 kHz仍有-31.2 dB.为了得到最低的工作电压，仿真了输出基准电压VREF与电源电压的关系，如图7(f)所示.可以看出，本文设计的带隙基准最低的工作电压为2.8 V.

表1对比了本文设计的带隙基准与已报道的带隙基准电路的性能.其中，文献[13-15]采用了双带隙核心电路的结构，与本文结构相似，但因为本文的带隙基准电路使用了电流镜自偏置的简单结构，电路消耗了更少的电流.本文借鉴了文献[16]的带隙结构，但文献[16]的电路由于工作在亚阈值区，功耗很低，消耗的电流为0.48 μA，但其温度性能变化很大，平均温度性能相比本文也较差.从对比结果来看，本文设计的带隙基准在温度性能和功耗上得到了很好的折中.

图7 后仿真结果Fig.7 Results of post simulations

文献工艺/μm温度范围/℃电流消耗/μA平均温度系数/(ppm·℃-1)参考电压/VPSR/dB供电电压/V面积/mm2文献[13]0.13-40～1201209.30.735-30@100kHz1.20.063文献[14]0.18-40～1203615.90.767-84@DC1.20.036文献[15]0.250～1005019.50.536-25.5@10kHz1.00.108文献[16]0.090～1000.4853.10.720-52@DC1.20.028本文0.18-40～1259.814.31.200-37@DC3.30.066

4 结 论

本文设计了一个新颖的结构简单易实现的带隙基准源.探讨了基于电流比例减法实现曲率补偿的合理性，并提出了新颖的双带隙结构的带隙基准源设计.通过推导一种新型电流模带隙结构电路在饱和区工作时的温度特性，验证了与改进的传统电流模带隙结构的二阶温度系数存在不同，并实现了电流比例相减的曲率补偿电路，得到高阶温度补偿的基准电压.相比已有的设计，通过采用电流镜自偏置结构，在降低电路设计复杂度的同时，也在很大程度上减小了电流消耗.仿真结果和对比表明，本文设计的带隙基准源在温度性能、设计复杂度和功耗上均有很好的折衷，适用于对精度、功耗和设计复杂度都有要求的电路.

[1] 幸新鹏,李冬梅,王志华.CMOS带隙基准源研究现状[J].微电子学,2008,38(1):57-63,71.

XING Xinpeng,LI Dongmei,WANG Zhihua.An overview of the research on CMOS bandgap referece sources[J].Microelectronics,2008,38(1):57-63,71.(ln Chinese)

[2] KUIJK K E.A precision reference voltage source[J].IEEE Journal of Solid-State Circuits,1973,8(3):222-226.

[3] 程军,陈贵灿.两种新型CMOS带隙基准电路[J].微电子学与计算机,2003,20(7):67-70.

CHENG Jun,CHEN Guican.Two CMOS bandgap reference circuits[J].Microelectronics & Computer,2003,20(7):67-70.(ln Chinese)

[4] KA N L,MOK P K T,CHI Y L.A 2-V 23-uA 5.3ppm/℃ curvature-compensated CMOS bandgap voltage reference[J].IEEE Journal of Solid-State Circuits,2003,38(3):561-564.

[5] HUANG Y,ZHU L,CHEUNG C,etal.A curvature-compensation technique based on the difference of Si and SiGe junction voltages for bandgap voltage circuits[C]//2014 IEEE International Symposium on Circuits and Systems (ISCAS).Melbourne,Australia:IEEE,2014:914-917.

[6] LEE I,KIM G,KIM W.Exponential curvature-compensated BiCMOS bandgap references[J].IEEE Joural of Solid-State Circuits,1994,29(11):1396-1403.

[7] CHEN X F,LIU F H,ZOU X C,etal.A linearized VBE bandgap voltage reference with wide temperature range[C]//2013 IEEE 10th International Conference on ASIC.Shenzhen,China:IEEE,2013:1-4.

[8] CHARALAMBOS M A,SAVVAS K,JULIUS G.A novel wide-temperature-range,3.9ppm/℃ CMOS bandgap reference circuit[J].IEEE Journal of Solid-State Circuits,2012,47(2):574-581.

[9] LI J H,ZHANG X B,YU M Y.A 1.2-V piecewise curvature-corrected bandgap reference in 0.5 μm CMOS process[J].IEEE Transactions on Very Large Scale Integration (VLSI) Systems,2011,19(6):1118-1122.

[10]ZHANG Y W,ZHU J,SUN W F,etal.1 ppm/℃ bandgap with multipoint curvature-compensation technique for HVIC[J].Electronics Letters,2014,50(25):1908-1910.

[11]HUANG Y,CHEUNG C,NAJAFIZADEH L.A multi-piecewise curvature-corrected technique for bandgap reference circuits[C]//2013 IEEE 56th International Midwest Symposium on Circiuts and Systems (MWSCAS).Columbus,Ohio,USA:IEEE,2013:305-308.

[12]代国定,徐洋,李卫敏,等.高性能分段温度曲率补偿基准电压源设计[J].浙江大学学报:工学版,2010,44(11):2142-2147.

DAI Gouding,XU Yang,LI Weimin,etal.Design of high performance bandgap reference based on piecewise temperature curvature compensated technology[J].Journal of Zhejiang University:Engineering Science,2010,44(11):2142-2147.(ln Chinese)

[13]DUAN Q Z,ROH J J.A 1.2-V 4.2-ppm/℃ high-order curvature-compensated CMOS bandgap reference[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2015,62(3):662-670.

[14]MA B,YU F Q.A novel 1.2-V 4.5-ppm/℃ curvature-compensated CMOS bandgap reference[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2014,61(4):1026-1035.

[15]KER M D,CHEN J S.New curvature-compensation technique for CMOS bandgap reference with sub-1-V operation[J].IEEE Transactions on Circuits and Systems II:Express Briefs,2006,53(8):667-671.

[16]LEE K K,LANDE T S,HäFLIGER P D.A sub-uW bandgap reference circuit with an inherent curvature-compensation property[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2015,62(1):1-9.

CMOS Bandgap Reference of Low-power-consumption Double-bandgap Structures

XIAO Jingbo1 2，CHEN Min1，ZHANG Chengbin1，LIU Yunchao1，CHEN Jie1†

(1.Institute of Microelectronics of Chinese Academy of Science，Beijing 100029，China；2.University of Chinese Academy of Sciences，Beijing 100049，China)

With the development of system on chip (SOC),the precision and power consumption requirements of bandgap reference are becoming more stringent.Until now,high order temperature compensations still have some restrictions in the process compatibility,design complexity and power consumption.In this paper,the temperature characteristic of a new current mode bandgap reference operating in saturated region is derived,and effective curvature compensation is implemented by current ratio subtraction in the output branch circuits with double bandgap structures.Thus,a new CMOS bandgap reference of double bandgap structures is implemented.Layout area of the bandgap reference is 0.066 mm2in GSMC 0.18 μm process.The results of Monte Carlo post-simulations show that the average temperature coefficient is 14.27 ppm/℃ in the temperature range from -40～125 ℃,and the average reference voltage is 1.201 V at 27 ℃.The average static current is 9.865 μA and the power supply rejection is -37.21 dB at 3.3 V operating voltage.The bandgap reference designed in this paper has the characteristics of high precision,low power consumption and simple structure,which indicates that it is a better choice for SOC.

bandgap voltage reference；curvature compensation；temperature coefficient；low power consumption

1674-2474(2017)08-0124-07

10.16339/j.cnki.hdxbzkb.2017.08.019

2017-01-11

国家重点基础研究发展规划项目(973项目)(2015CB352103),National Basic Research Program of China(973 Program)(2015CB352103)

肖璟博(1991-)，男，江西萍乡人，中国科学院微电子所，中国科学院大学博士研究生

†通信联系人,Email：jchen@ime.ac.cn

TN402

A