基于5阶球面最简相径的改进型容积卡尔曼滤波在SINS/DVL组合导航中的应用

徐晓苏，董 亚，童金武，代 维

（1. 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2. 东南大学 仪器科学与工程学院，南京 210096）

基于5阶球面最简相径的改进型容积卡尔曼滤波在SINS/DVL组合导航中的应用

徐晓苏1,2，董 亚1,2，童金武1,2，代 维1,2

（1. 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2. 东南大学 仪器科学与工程学院，南京 210096）

为提高水下SINS/DVL组合导航系统的精度，建立了捷联惯性导航系统(SINS)的非线性误差模型，并建立多普勒测速仪的误差方程，以SINS为主导航设备建立SINS/DVL组合导航系统模型。设计了5阶球面最简相径容积卡尔曼滤波器，采用了球面最简相径采样规则改进容积卡尔曼滤波，并应用于SINS/DVL组合导航系统中。通过数学平台仿真验证了5阶球面最简相径容积卡尔曼滤波方法有效性，仿真结果表明：该方法能够有效提高SINS/DVL组合导航系统的精度，且稳定性好。

组合导航；非线性系统；球面最简相径；容积卡尔曼滤波

水下自主航行器（AUV）无论在军用还是民用领域都有着广泛的应用前景[1]。单一的惯性导航系统（INS）虽然具有强自主性，强隐蔽性等优点，但其系统误差会随时间积累，长时间工作会导致其导航精度下降而无法满足导航精度要求。组合导航技术是AUV研究的一个重要分支已经越来越被重视。SINS/DVL组合导航系统利用DVL速度信息对SINS导航误差进行抑制，能够获得较高的导航精度，因此SINS/DVL组合导航系统常被应用于水下AUV中[2]。

SINS/DVL组合导航系统一般采用线性卡尔曼滤波（KF）、扩展卡尔曼滤波（EKF）、容积卡尔曼滤波（CKF）[2-3]。在很多环境中，例如在姿态失准角较大时，经典的线性误差模型和标准卡尔曼滤波方法的使用具有局限性[4-5]，线性卡尔曼滤波技术在处理线性系统时能保证精度，但是当系统的数学模型是非线性模型时，线性卡尔曼滤波技术的精度无法满足。EKF只采用其非线性函数泰勒级数展开的第一项，忽略其他高阶项，从而达到函数线性近似的目的，但是这样会引入高阶项带来的误差，需要计算雅各比矩阵，精度受到了很大限制[6,8]。CKF采用的是卡尔曼滤波结构的高斯滤波方程，根据容积采样规则解决高斯滤波中的多维积分问题，但5阶标准CKF会导致计算量过大，且当状态变量维数增加时其鲁棒性不是很好[7,12]。

本研究针对以上问题，采用球面最简相径（SSR）采样规则改进标准的CKF算法，并选用5阶改进的CKF，进一步提高了组合导航系统的导航精度。将标准CKF和改进后的CKF滤波后的导航精度进行仿真比较，结果表明，改进后的CKF比标准CKF滤波效果更好，系统的导航精度更高[10-11]。

1 SINS/DVL组合导航系统模型

1.1 SINS误差数学模型

导航坐标系(n系)选用东-北-天地理坐标系，载体坐标系为b系，计算导航坐标系记为n′系。真实姿态角φ=[φE,φN,φU]，真实速度，真实地理坐标P=[L,λ,H]。

1.2 DVL误差数学模型

多普勒测速仪(DVL)是根据多普勒效应，利用超声换能器发射的超声波来测量载体速度的仪器[5]。DVL的测速误差主要包含标度因数误差δKc、偏流角误差δ∇和随机测量误差δVDVL，考虑到偏流角误差对DVL测速误差影响较小，不考虑偏流角误差，可得速度方程为：

式中：βV、βK分别表示DVL随机测量误差和刻度系数误差的相关时间；wV、wK为其对应的零均值高斯白噪声。

1.3 组合导航滤波模型

由于惯导系统天向通道不稳定，且DVL对天向的测速误差较大忽略高度通道的状态量[6]，对于SINS系统，选取12维状态变量为：

对于DVL选取标度因数误差和随机常值测量误差作为状态量，即：。将系统的非线性状态方程简记为：

式中：w(t)为系统的过程噪声且w( t)～N[0,Q( t)δ(t-τ)]，Q(t)为系统过程噪声向量的方差强度矩阵。

选取系统的观测量为导航坐标系下捷联解算速度和DVL的速度的差值，并且由于惯导系统天向通道不稳定，且DVL对天向的测速误差较大，本文只考虑水平通道，即只取速度的前两维。

式中：Vn为导航坐标系下速度的真实值，δKc为DVL的刻度系数误差，δVDVL为DVL的随机测量误差。因此量测方程为：

将此量测方程简记为：

式中：u(t)为系统的观测噪声，且u(t)～N[0,R(t)δ(t-τ)]，R(t)为观测向量的方差强度矩阵。

以采样周期Ts作为滤波周期，并以Ts为步长，对系统的状态方程和量测方程进行离散化，得到系统的非线性滤波模型，并简记为：

式中：wk为随机系统过程噪声并且wk～N(0,Qk)，Qk为系统过程噪声序列的方差阵；uk为系统的随机观测噪声并且uk～N (0,Rk)，Rk为系统的观测噪声序列的方差阵。

2 五阶SSRCKF滤波算法

经典的容积卡尔曼滤波（CKF）将积分式用权值与相应采样点函数值的乘积来近似，避免了计算机进行高维积分运算，可显著减少计算机的计算量，提高滤波效率。对于精度要求不高的系统，标准3阶CKF可以满足，且采样点数量较少，滤波效率较高，但如果要求更高阶的系统精度，需要5阶CKF或更高阶的滤波器，此时采样点的数量会随之增加，这就导致计算量增加，滤波效率变低。此外文献[8]指出，当系统的状态量维度较高时，标准5阶CKF的部分采样点权值会变成负值，这种情况可能导致滤波器发散，影响滤波效果。为解决上述问题，提高滤波的精度和效率，本文在经典CKF的基础上，采用SSR容积采样规则，对标准CKF进行改进。

2.1 SSR容积采样规则

高斯滤波积分可归纳成：

采用SSR容积采样规则，求解球面积分S( R)。对于拥有n维状态量的系统，求解过程如下：取一组n维向

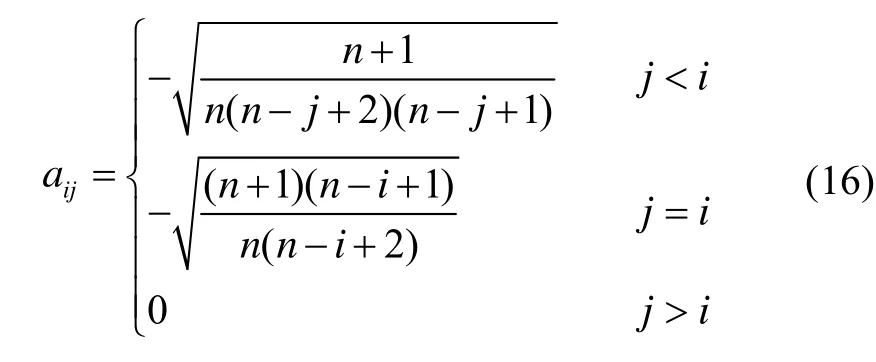
将向量ai的中点投影到球面Un得到以下序列：

文献[8]指出，标准5阶CKF在系统维度n＞4时会出现权值为负值的现象，这将导致滤波器发散。相比较而言，虽然通过SSR采样规则改进的5阶SSRCKF方法在n＞7时权值也可能为负值，但当n→∞时，上述权值点将趋于零，因此5阶SSRCKF具有较强的鲁棒性。本文系统的状态变量选用16维，表1[8]给出了当n=16时，3阶CKF、5阶CKF、3阶SSRCKF和5阶SSRCKF四种算法的采样点数量，显然5阶SSRCKF算法与5阶CKF算法相比，采样点数目大幅度减少，同时可以使滤波器达到5阶精度。因此本文选用5阶SSRCKF算法。

表1 四种算法的采样点数目Tab.1 Point numbers of different algorithm

2.2 SSRCKF滤波器

基于SSR采样规则改进的CKF在估计精度上明显优于标准CKF，尤其在计算量上。5阶SSRCKF既能使得滤波精度达到5阶，并且其采样点数目较少，能够显著提高滤波效率。改进后的五阶SSRCKF滤波算法如下：

式(9)和(13)已经给出本文组合导航系统的非线性滤波方程，且系统过程噪声和观测噪声已假设为高斯白噪声，可用均值和方差完全表达成高斯分布，因此可以使用高斯滤波过程处理，其一般形式如下：

式(20)种的各变量可用如下积分形式表示：

上述变量的运算可归纳成统一的多维积分形式I( f)，因此只需求得该积分的近似解就可完成上述高斯滤波过程，而I( f)可通过SSR溶剂采样规则近似。以下给出5阶SSRCKF的滤波过程：

3 仿真实验与分析

本文SINS/DVL组合导航滤波过程采用间接滤波法，即采用SINS和DVL水平方向速度的差值为观测量，观测量通过5阶SSRCKF进行最优估计，将估计后的系统误差对SINS系统进行反馈校正，最终输出导航参数。具体流程如图1所示。

图1 SINS/DVL组合导航滤波原理框图Fig.1 Schematic of SINS/DVL integrated navigation

针对此SINS/DVL的组合导航系统分别采用3阶标准CKF算法和改进后的5阶SSRCKF算法进行了2h的MATLAB仿真。设定系统工作的初始位置为东经118°，北纬32°；①SINS系统：系统陀螺的常值偏移和随机偏移均设为0.05 (°)/h，加速度计的常值漂移和随机漂移均设为50μ，水平初始姿态角为0°，航向角设为北偏东30°，初始姿态角误差分别为1°、1°、10°，北向速度和东向速度的初始偏差为0 m/s；②DVL系统：速度偏移误差δVDVL= 0.10 m/s，标度因数误差δKc=0.001，DVL的速度偏移的相关时间和刻度系数误差的相关时间分别取为100 s。SINS的采样周期为0.01 s，DVL的采样周期为1 s，CKF的滤波周期设置为1 s。载体以5 m/s的速度沿直线匀速行驶一段时间后，绕圆弧依次进行90°的左转和右转，转向时间为120 s，两次转向间的运动时间为1000 s，两次转向后载体继续沿直线运动，仿真时间为7200 s。

3阶标准CKF以及本文改进的5阶SSRCKF的仿真的姿态角、运动线速度和位置误差如图2～4所示，图中φx、φy、φz分别表示纵摇、横摇和航向失准角，δVE、δVN分别为东向和北向速度误差，δpE、δpN分别为东向和北向（经纬度方向）的位置误差。

从图2的姿态角误差仿真曲线可以看出，3阶CKF算法和改进后的5阶SSRCKF算法的水平失准角都有较高的精度和稳定性，但改进后的5阶SSRCKF算法的精度明显高于3阶CKF算法的精度，其水平误差角稳定在±0.01°以内，航向角误差稳定在±0.1°以内。

从图3的速度误差曲线可以看出，改进后的5阶SSRCKF算法速度误差稳定性和精度都高于3阶CKF算法，其误差量稳定在±0.25 m/s之间。

从图4的位置误差曲线仿真图可以看出：在7200 s的仿真时间内，3阶CKF的北向位置误差在-150～100 m之间，5阶SSRCKF算法的北向位置误差范围在-50～50 m之间，后者精度显著提高；3阶CKF的东向位置误差在-150～10 m之间，5阶SSRCKF算法东向位置误差在-50～10 m之间，5阶SSRCKF算法的精度明显高于3阶CKF算法。

综上所述，5阶SSRCKF显著提高了SINS/DVL组合导航系统的导航精度。

图2 姿态角误差仿真曲线Fig.2 Simulation curves of attitude angle errors

图3 水平方向速度误差仿真曲线Fig.3 Simulation curves of horizontal velocity errors

图4 位置误差仿真曲线Fig.4 Simulation curves of position errors

从以上的仿真实验结果可知：采用5阶SSR采样规则改进的CKF算法，在继承标准CKF算法的基础上，进一步提高了组合导航系统的导航精度，同时解决了标准CKF算法为提高精度而采用高阶算法时，其计算量大大增多的问题。相比之下，改进后的5阶SSRCKF算法比3阶标准CKF算法的导航精度高，更适用于导航系统精度要求较高的系统。

4 结 论

本文为了提高SINS/DVL组合导航系统精度，根据捷联惯性导航系统（SINS）的非线性误差模型和多普勒测速仪（DVL）的测速原理及其误差方程，以SINS为主导航设备且以DVL辅助导航，建立SINS/DVL组合导航系统模型。采用球面最简相径（SSR）采样规则改进CKF滤波方法，通过改变其采样规则，减少了CKF算法的采样点数量，该方法相比于3阶CKF导航精度较高，相比于5阶CKF计算量小，计算效率显著增加。在数学平台下进行7200 s的动基座仿真，仿真结果表明：5阶SSR改进型CKF方法能够有效提高SINS/DVL组合导航系统的精度，且稳定性好。

（References）：

[1] 李厚全, 刘莫尘, 伍志海, 等. 球面单形平方根无迹粒子滤波在拖曳合成孔径声纳组合导航中的应用[J]. 中国惯性技术学报, 2014, 22(4): 531-535.Li Hou-quan, Liu Mo-chen, Wu Zhi-hai, et al. Spherical simplex squareroot unscented particle filter used in integrated navigation system of synthetic aperture sonar[J]. Journal of Chinese Inertial Technology, 2014，22(4): 531-535.

[2] 黄莺. 基于CKF的SINS/DVL组合导航系统设计与仿真[D]. 哈尔滨:哈尔滨工程大学, 2013.Huang Ying. Design and simulation of SINS/DVL integrated navigation system based on CKF[D]. Harbin: Harbin Engineering University, 2013.

[3] Cao Jie, Liu Fan-ming, Chen Qin, et al.SINS/DVL integrated navigation technology in autonomous underwater vehicle[J]. Navigation of China, 2004, 59(2):55-59.

[4] Yang Bo, Xu Xiao-su, Zhang Tao, et al.Novel SINS initial alignment method under large misalignment angles and uncertain noise based on nonlinear filter[J]. Mathematical Problems in Engineering, 2017: 1-14.

[5] 徐晓苏, 潘永飞, 邹海军. 基于自适应滤波SINS/DVL组合导航系统[J].华中科技大学学报(自然科学版),2015(3): 95-99, 106.Xu Xiao-su, Pan Yong-fei, Zou Hai-jun.SINS/DVL integrated navigation system based on adaptive filtering[J].Journal of Chinese Inertial Technology,2015(3): 95-99, 106.

[6] Gao Wei, Li Jing-chun. Adaptive Kalman filtering for the integrated SINS/DVL system[J]. Journal of Computational Information Systems, 2013, 16(9):6443- 6450.

[7] Wang Xiao-xu, Liang Yan, Pan Quan, et al. Gaussian filter for nonlinear systems with one-step randomly delayed measurements[J]. Automatica, 2013, 49(4):976-986.

[8] Wang Shi-yuan, Feng Jiu-chao. Spherical simplex-radial cubature Kalman filter[J]. IEEE Signal Processing Letters,2014, 21(1): 43-46.

[9] Jia B, Xin M, Cheng Y. High-degree cubature Kalman filter[J]. Automatica,2013, 49(2): 510-518.

[10] Zhang Yong-gang, Huang Yu-long, Wu Zhe-min, et al. Seventh-degree spherical simplex-radial cubature Kalman filter[C]//Proceedings of the 33rd Chinese Control Conference. 2014: 2513-2517.

[11] Arasaratnam I, Haykin S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269.

[12] Wang Lei, Cheng Xiang-hong, Li Shuangxi, et al. Adaptive interacting multiple model filter for AUV integrated navigation[J]. Journal of Chinese Inertial Technology, 2016, 24(4): 511- 515.

Improved fifth-degree spherical simplex sadial cubature Kalman filter in SINS/DVL integrated navigation

XU Xiao-su1,2, DONG Ya1,2, TONG Jin-wu1,2, DAI Wei1,2
(1. Key Laboratory of Micro-inertial Instrument and Advanced Navigation Technology, Ministry of Education, Southeast University,Nanjing 210096, China; 2. School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China)

In order to improve the accuracy of SINS/DVL integrated navigation system, a SINS/DVL integrated navigation system model is built based on establishing the nonlinear error model of SINS and the error equation of the Doppler velocity log (DVL). To further improve the navigation accuracy, a fifth-degree cubature Kalman filter is applied. In view that conventional fifth-degree cubature Kalman filter has too large computation amount and relative poor robustness, a fifth-degree spherical simplex radial (SSR) cubature Kalman filter is designed, which adopts the SSR rule to change the sampling rule and reduce the number of sampling points. Simulation results show that the proposed method can effectively improve the accuracy of the SINS/DVL integrated navigation system and has better stability.

integrated navigation; nonlinear system; spherical simplex radial; cubature Kalman filter

U666.1

：A

1005-6734(2017)03-0343-06

10.13695/j.cnki.12-1222/o3.2017.03.012

2017-03-07；

：2017-05-25

国家自然科学基金项目（51175082，61473085）

徐晓苏（1961—），男，博士生导师，从事测控技术与导航定位领域的研究。E-mail: xxs@seu.edu.cn