UWB测距的NLOS误差削弱方法

王长强，徐爱功 ，隋 心，2

(1.辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2.武汉大学 卫星导航定位技术研究中心，武汉 430079)

UWB测距的NLOS误差削弱方法

王长强1，徐爱功1，隋 心1，2

(1.辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000；2.武汉大学 卫星导航定位技术研究中心，武汉 430079)

为了提高UWB室内定位系统的精度，提出一种偏移卡尔曼滤波方法：将测距残差与卡尔曼滤波结合，鉴别出NLOS误差，并将残差值加入到卡尔曼滤波的迭代中以修正卡尔曼滤波的异常值，从而实时抑制NLOS误差，提高UWB室内定位精度。实验结果表明，该方法能有效抑制NLOS误差的影响，提高NLOS传播环境下的定位精度。

UWB；非视距误差；测距残差；卡尔曼滤波

0 引言

随着无线通信技术的发展，无线定位技术引起了各国公司及研究人员的广泛关注。基于超宽带(ultra wide band，UWB)的无线定位系统利用UWB信号高达ns级别的时间分辨率，结合到达时间(time of arrival，TOA)，其测距结果理论上可实现cm级别的定位精度[1]。UWB无线信号具有其他众多短距离定位技术无法相比的穿透能力，可以很好地完成室内和障碍物遮挡环境下的测距与定位[2-3]；因此，基于UWB的TOA定位法是解决室内或者障碍物很多的环境中定位问题的一个很好的解决方案。但是，其无线定位测距性能也受到UWB信号传播特性的影响，其中非视距(non line of sight，NLOS)传播是造成TOA测距误差的主要原因；所以深入研究NLOS误差对测距精度的影响，对更好地应用UWB的实时动态定位技术具有重大意义。

文献[4]所提算法未考虑非视距误差的影响，且需要大量冗余信息才能确保定位精度；文献[5]中的Wylie法利用TOA测量值的时间历史来重构视距的TOA测量值，定位误差较小但不能实时定位；文献[6]提出根据新息来调整卡尔曼滤波器的增益，以此来滤除NLOS误差而得到较精确的测量值，但是该方法中的各个参数不能自适应调整；文献[7]针对测距中的NLOS误差，将TOA值和NLOS误差值作为卡尔曼滤波的2个状态向量直接估计出NLOS误差，该方法简单、算法复杂度低，但是根据NLOS误差的统计特性来看，在某些复杂信道环境中，模型系数并不唯一确定，直接估计NLOS误差值并不符合实际情况；文献[5，8]提出用具有代表性的测量样本的标准差和测量噪声的标准差鉴别NLOS误差，提高测量精度，但这种方法引入了时间延迟，较复杂而且不能进行实时定位；文献[9]采用偏移卡尔曼滤波(biased Kalman filter，BKF)处理测量数据，其中将NLOS误差视为是服从指数分布的，并不符合其误差特点(NLOS误差的分布模型没有统一定论)，且将测量噪声的均值加入到卡尔曼滤波计算中，这种做法需要大量实验数据且不具有代表性，不能适用于任意非视距环境。

本文将卡尔曼滤波与测距残差相结合，通过计算观测值与卡尔曼滤波预测值之间的差，与设定阈值比较后鉴别有无NLOS存在，如果存在NLOS误差，将残差值加入卡尔曼滤波计算中，修正异常值，得到抑制NLOS误差的测量值，形成一种新的偏移卡尔曼滤波方法，处理非视距情况下测量到的数据，以期实现实时动态精确定位。

1 NLOS对室内定位的影响

无论是在室外的蜂窝网定位还是室内定位，定位基站与移动站之间的直射路径往往可能受到阻挡，由于实际环境中的障碍物阻挡或者多径干扰而造成的误差称为非视距误差，这时它们之间信号的传播将是非视距传播，其路径轨迹如图1所示。

假设在视距(line of sight，LOS)信道环境下，移动站在ti时刻与k基站的TOA测量距离值为rk(ti)， 具体可表示为

rk(ti)=Lk(ti)+nk(ti)。

(1)

式中：Lk(ti)为ti时刻移动站与k基站的真实距离；nk(ti)为标准时间误差，是标准时间偏差所造成的测距误差，不仅包括脉冲信号在UWB流动站和UWB基准站中的固定时延误差、UWB器件误差和UWB逐次启动误差，而且还与脉冲信号传播的距离、温度等外界环境有关[10-11]，该误差通常认为是均值为零、标准差很小的高斯随机噪声，可以通过多项式拟合技术剔除。而在NLOS环境中，除了标准时间误差之外，还包括了NLOS引起的随机测量误差。因此，NLOS环境下TOA测量值可以表示为

rk(ti)=Lk(ti)+nk(ti)+NLOSk(ti)。

(2)

式中NLOSk(ti)为非视距误差，其在不同的信道环境下有可能服从指数分布、均匀、高斯或δ分布。NLOSk(ti)仅与电波的传播环境有关，通过提高系统的接收机的测量精度是无法消除该NLOS误差的。

在NLOS误差影响情况下，测量值不能真实反映实际情况(角度、距离等)；NLOS误差是影响定位精度的主要原因。若定位过程中有NLOS误差，在移动站到基站的测量值中会产生正的误差分量，将这种较大误差的测量值用于位置估计时，势必会造成定位精度显著下降，如图2所示。

图中黑色区域表示NLOS误差对定位结果造成的影响——本来应该定位于一个点，受到误差影响形成现在的状态。因此要得到稳定可靠的定位服务，NLOS误差是必须解决的一个关键问题，有必要对信号的非视距传播进行研究。

2 基于偏移卡尔曼滤波的NLOS误差鉴别与抑制方法

随着无线定位技术的飞速发展，卡尔曼滤波器被逐渐应用于动态定位方面。卡尔曼滤波能够从一系列的不完全及包含噪声的测量中，估计动态系统的状态，是一种高效率的递归滤波器(自回归滤波器)。

2.1 卡尔曼滤波基本原理

卡尔曼滤波包括2个阶段：预测和更新。在预测阶段，滤波器通过使用上一状态的估计对当前状态进行估计；在更新阶段，滤波器利用当前状态的观测值优化在预测阶段获得的预测值，以获得一个更精确的新估计值。卡尔曼滤波器的系统状态方程和测量方程[12]分别为：

Xk=AXk-1+Bμk-1+Γk,k-1wk-1；

(3)

Yk=HkXk+vk。

(4)

式中：Xk、Yk分别表示状态向量和观测向量；A为状态转移矩阵；B为可选的控制输入μ的增益(本文中将其设置为0)；Γk,k-1为状态噪声系数矩阵；wk-1、vk分别为状态噪声序列与观测噪声序列；Hk为观测向量系数矩阵。

状态方程和测量方程将第k时刻的观测值、观测值历史信息和状态值之间联系起来。因此只需提供一个初值状态向量值和设定一个估计误差协方差，就可以通过迭代根据测量值序列估计出相应时间点上的状态值。

卡尔曼滤波迭代的具体过程为：

(5)

(6)

(7)

(8)

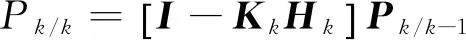
(9)

式中：Q为ωk-1的协方差阵；R为vk的协方差阵；Kk为卡尔曼增益；I为单位阵。

2.2 NLOS误差鉴别与抑制方法

在UWB的室内环境下，NLOS误差并不能通过模型表示出来，可以通过计算测量测距残差值实时描述NLOS的数据变化情况。

(10)

如果存在NLOS误差，将测距残差加入到下一时刻的卡尔曼滤波计算，改正卡尔曼滤波的异常值。设测距残差值为C=Δd， 故卡尔曼滤波式(5)～式(9)需要考虑到非零残差值C的存在，其公式(8)可重新推导如下：

1)测量值向量Yk的估计方法为

(11)

式中λ为单位向量。

2)测量值向量Yk和Yk/k-1之间的差为

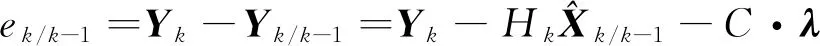
(12)

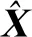
(13)

这种方法的阈值容易确定，且由于残差值C的作用，避免了将NLOS误差带入到卡尔曼滤波迭代过程中。通过计算测距残差，实时描述NLOS误差的数据变化情况，符合NLOS误差具有随机性的特点，没有引入时间延迟等其他不必要的参数；使得滤波精度进一步提高。

3 实验及结果分析

在实际生活中，大多数情况都是既存在视距误差又存在非视距误差的影响，本文实验环境就选定这种情况，利用4个UWB模块、全站仪和笔记本电脑(安装定位程序)进行动态定位实验。其中设定UWB模块采样时间间隔为T(T=0.5 s)， 路径上的各拐点及UWB参考基准站坐标已预先用全站仪测得，实验环境如图3所示，室内定位路径轨迹平面图是一个矩形，移动站MS以1 m/s的速度沿着已知的四边形ABCD运动。

当移动站的UWB没有被墙柱遮挡时，移动站只受到视距误差(标准时间偏差)影响；当移动站被墙柱遮挡时，会同时受到视距和非视距误差影响，实验结果如图4～图6所示。

图4中：灰色折线为原始观测数据测距误差；0～1 500次是视距环境下的测距误差，该阶段移动站MS属于静止状态，并且与所有基站间相互通视，均是LOS路径：从图中可以看出原始数据会有约为0.2 m的偏差，其误差来源主要为标准时间偏差，该类误差须通过多项式平滑的方法剔除；1 500次以后是间断性非视线测距，NLOS误差会

严重影响UWB测距精度，最大误差可达0.5 m。采用本文算法对NLOS误差进行处理后，测距误差明显减小，可控制在0.2 m以内。

如图5、图6所示，实验将NLOS误差削弱前后的定位精度进行对比，并将经典卡尔曼滤波处理测距结果解算轨迹和经过本文算法处理测距之后的解算轨迹进行比较。从图5可以看出，利用本文算法处理之后解算的轨迹明显贴近于真实轨迹；图6为经过NLOS误差削弱之后的定位结果，可以看出，定位结果的精度得到了明显提升，可以达到0.2 m，最大误差不超过0.25 m。由此可见，使用本文修正的测距结果进行动态定位，其定位精度能够得到较大提高。

4 结束语

NLOS环境下UWB信号的非视距传播会严重影响TOA测距精度，针对该问题在已有的偏移卡尔曼滤波方法基础上，将测距残差与卡尔曼滤波结合，通过测距残差鉴别出NLOS误差，并将动态变化的残差值加入到卡尔曼滤波的迭代中，修正卡尔曼滤波的异常值，从而抑制NLOS误差，提高UWB室内定位精度。此算法通过判决直接修正异常新息，计算简单，无需调整滤波增益系数，且不需要样本标准差的先验信息，不需引入时间延迟。

[1] GEZICI S，TIAN Z，GIANNAKIS G B，et al.Location via ultra-wideband radios：a look at positioning aspects of future sensor network[J].IEEE Signal Processing Magazine，2005，43(22)：70-84.

[2] PAHLAVAN K，LI X，MAKELA J P.Indoor geolocation science and technology[J].IEEE Communication Magazine，2002，40(2)：112-118.

[3] ABDULRAHMAN A，ABDULMALIK A S，MANSOUR A，et al.Ultra wideband indoor positioning technologies analysis and recent advances[J].Sensors，2016，16(5)：707.

[4] DON J T.Statistical theory of passive location systems[J].IEEE Trans on Aerospace and Electronic Systems，1984，20(2)：183-198.

[5] WYLIE M P，HOLTZMAN J.The non-line of sight of sight problem in mobile location estimation[C]//The Institute of Electrical and Electronic Engineers(IEEE).Proceedings of IEEE International Conference on Universal Personal Communications(ICUPC 1996 ).Piscataway，USA：IEEE，1996：827-831.

[6] 李静，刘据.用卡尔曼滤波器消除TOA中NLOS误差的三种方法[J].通信学报，2005，26(1)：130-135.

[7] 张美杨，季仲梅，王建辉. 基于Kalman滤波器的非视距误差已知算法[J].计算机工程，2010，36(11)：291-293.

[8] BAO L，AHMCD K，TSUJI H.Mobile location estimator with NLOS mitigation using Kalman filter[C]//The Institute of Electrical and Electronic Engineers(IEEE).Proceedings of IEEE Wireless Communication and Networking Conference(WCNC 2003).Piscataway，USA：IEEE，2003：1969-1973.

[9] WANN C D，HSUEH C S.Non-line of sight error mitigation in ultra-wideband ranging systems using biased Kalman filtering[J].Journal of Signal Processing Systems，2011，64(3)：389-400.

[10]RUI Z H，FABIAN H，LEONHARD R.Inertial sensor based indoor localization and monitoring system for emergency responders[J].IEEE Sensors Journal，2013，13(2)：838-848.

[11]MANON K，JEROEN D H，THOMAS B S.Indoor positioning using ultrawideband and inertial measurements[J].IEEE Transactions on Vehicular Technology，2015，64(4)：1293-1303.

[12]GREWAL M S，ANDREWS A P.Kalman filtering：theory and practice[M].4th ed.USA：Wiley，2014：37-235.

[13]WANN C D，YEH Y J，HSUEH C S.Hybrid TDOA/AOA indoor positioning and tracking using extended Kalman filters [C]//The Institute of Electrical and Electronic Engineers(IEEE).Proceedings of IEEE Vehicular Technology Conference(VETECS 2006).Kaohsiung：IEEE，2006：1058-1062.

A method of NLOS error inhibition for UWB ranging

WANGChangqiang1，XUAigong1，SUIXin1，2

(1.School of Geomatics，Liaoning Technical University，Fuxin，Liaoning 123000，China；2.Research Center of GNSS，Wuhan University，Wuhan 430079，China)

In order to improve the accuracy of UWB indoor positioning system，the paper proposed a method of biased Kalman filtering：Kalman filter was combined with ranging residual，the NLOS error was identified，and then the residual was added to the interation of Kalman filter to modify the abnormal values for real-time restraining NLOS errors and improving the indoor positioning accuracy of UWB. Experimentsal result showed that the proposed method ould effectively inhibit the influences of NLOS errors and improve the locationing accuracy under the environment of NLOS propagation.

UWB；NLOS error；ranging residual；Kalman filtering

2016-10-14

国家重点研发计划项目(2016YF C0803102)；辽宁省高等学校创新团队项目(LT2015013)。

王长强(1992—)，男，辽宁大连人，硕士研究生，研究方向为室内外定位导航及多传感器组合。

王长强，徐爱功，隋心.UWB测距的NLOS误差削弱方法[J].导航定位学报，2017，5(3)：24-27,32.(WANG Changqiang，XU Aigong，SUI Xin.A method of NLOS error inhibition for UWB ranging[J].Journal of Navigation and Positioning，2017，5(3)：24-27,32.)

10.16547/j.cnki.10-1096.20170306.

P228

A

2095-4999(2017)03-0024-05