一种载波扫频的伪随机码多径抑制方法

谢郁辰，徐成涛，唐小妹，王飞雪

(国防科学技术大学 卫星导航定位技术工程研究中心，长沙 410073)

一种载波扫频的伪随机码多径抑制方法

谢郁辰，徐成涛，唐小妹，王飞雪

(国防科学技术大学 卫星导航定位技术工程研究中心，长沙 410073)

针对BDS的地球同步轨道卫星存在的静态多径现象，即与中轨道卫星相比其多径误差难以通过传统的多径处理方法进行平均抑制的问题，提出了一种基于载波扫频的伪随机码多径抑制方法。通过载波线性扫频，接收机剥离信号载波后伪随机码的多径分量将呈现正弦包络的特性，从而在码相关器的相干积分输出结果中，实现对多径误差较好的抑制。还对扫频信号的参数进行了分析与研究，为载波扫频信号的设计提供了一定的参考。

静态多径；伪随机码；载波扫频；码相关器；多径抑制

0 引言

卫星导航接收机的测距误差受很多因素影响，如电离层延迟、对流层延迟、卫星星历误差、多径误差等[1]。随着各大卫星导航系统整体的升级换代，由电离层、对流层等引起的系统误差都可通过差分技术和高精度模型得到较大程度消除，而两台相同的接收机在即使仅在空间上分布有所不同，其多径误差就有明显差异，因此无法用差分方法进行抑制[2]，故多径误差是目前卫星导航高精度定位、测距接收机中误差主要来源[3]。

在对北斗卫星导航系统(BeiDou navigation satellite system，BDS)的长期观测中发现，中圆地球轨道(medium Earth orbit，MEO)卫星的多径误差在一定时长内呈现近似随机的特性，可以通过数据的平均得到较好的抑制；而地球静止轨道(geostationary Earth orbit，GEO)卫星由于轨道相对地面静止，与其他卫星相比其多径误差的变化周期增大到1 d左右，在较短时间内平均误差不为零，而是表现为固定的偏差值，难以同直达信号进行区分，称之为静态多径现象[4-5]。这一现象同样存在于广域增强系统(wide area augmentation system，WAAS)等全球定位系统(global positioning system，GPS)增强系统等其他地球同步轨道卫星系统之中。GEO卫星的静态多径现象难以通过传统方法，如观测站选址、天线设计等方法进行改善，恒星日滤波器[6]通过对卫星长时间的观测与数据处理，可以在一定程度上降低该类多径的影响，但这一方法依赖于长期固定位置的测量条件。文献[7]中提出了将导航系统GEO卫星信号采用固定载频变为随时间扫频的载波信号体制，并通过仿真验证了载波扫频可以改善对静态多径的抑制效果。

在此基础上，本文进一步推导了该方法对伪随机码相关函数的影响，并研究了不同的载波扫频周期下该方法对伪码多径分量相关函数幅值的抑制性能。理论推导与仿真表明，当载波随时间线性扫频时，接收信号进行载波剥离后，伪随机码的多径分量会呈现正弦包络的特性，使用传统码相关鉴别器进行相干积分时，多径分量的相关函数能够得到抑制，鉴相函数受多径影响而产生的变形能够得到改善。当载波扫频周期和扫频范围满足一定条件时，多径信号的相关函数能得到99.3%的抑制，基本消除其对码相关鉴别器的影响。另一方面，当载波扫频周期进一步缩短后，在一个相干积分时长内频率单调性改变时，相干积分对多径的抑制性能并不能持续改善，但总体趋势是随着扫频周期缩短，相干积分对多径的抑制效果提升，多径误差包络面积减小。因此本文也对载波扫频周期、多径时延与多径抑制性能的关系进行了分析与研究，为载波扫频信号参数的选取提供了一定参考。

1 理论推导

1.1 信号模型

假设直达信号时延为0，单路径反射[8]模型下，单路强多径相对直达信号多径时延为Δτ，当信号载波频率随时间变化时，信号的瞬时相位可以看作频率对时间的积分，暂不考虑接收机的动态引起的多普勒频移，则接收的信号为

(1)

式中：A为信号幅度；P为伪码符号；α为多径信号幅度与直达信号的幅度的比例系数；f(t)为信号的载波频率；φ0为直达信号初始相位；Δφ为由反射引起的相位变化；n(t)为传播信道的噪声。

下面分别对信号载波频率f(t)线性变化和正弦变化两种情况进行分析。

1.2 载波线性扫频

假设信号载波随时间线性扫频，频率f与时间t的函数关系，有

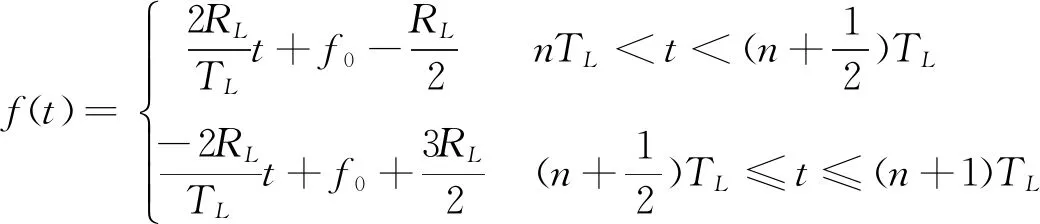
(2)

式中：RL为扫频范围为；TL为扫频周期；f0为载波中心频率。为保证信号频率的连续性，一个周期内载波频率先线性递增，再线性递减，斜率为2RL/TL。频率变化示意图如图1。

对于动态接收机，卫星发射载波扫频信号相当于增加了多普勒频移的动态应力阶数，从而对载波环的稳定跟踪产生一定负担，但稳定跟踪后的分析应与静态接收机一致。

此处假设接收机产生的本地信号能够跟踪接收信号的频率变化，则本地信号为

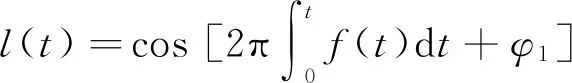
(3)

式中φ1为本地信号相位。接收信号与本地信号相乘，并低通滤波，可以实现载波剥离，即

s(t)= [r(t)·l(t)]LPF=d(t)+m(t)+n′(t)=

n′(t)+AP(t)cos (φ1-φ0-Δφ)+

(4)

式中：d(t)为直达分量；m(t)为多径分量；n′(t)为噪声项，其余参数定义同式(1)。

由于Δτ≪TL，因此Δτ时间段内信号频率可认为是单调变化，研究多径分量，频率线性递增时，有

m1(t)=αP(t-Δτ)

αAP(t-Δτ)cos (ωt+φ1)；

(5)

频率线性递减时，有

m2(t)=αP(t-Δτ)

αAP(t-Δτ)cos (ωt-φ2)。

(6)

由式(6)可以看出，伪码的多径分量经载波解调输出后有正弦包络的特性。再进行相干积分时，设相干积分时长为T，假设相干积分起点处信号频率线性递增，当积分时长T内信号频率单调性不发生变化时，积分结果为

[sin (ωT+φ1)-sin (φ1)]R(τ+Δτ)。

(7)

在传统码环跟踪环路(delay lock loop，DLL)中，由早码、晚码构造的鉴相函数为

D(τ)=IRE(τ)-IRL(τ)=

(8)

式中d为早晚码之间的间隔。当忽略载波跟踪误差时，φ1与φ0近似相等，若有τ=0，则D(τ)=0，可以通过构造鉴相函数的零点来进行码环跟踪，即

D(τ)=IRE(τ)-IRL(τ)=

(9)

多径信号存在时，鉴相函数也受到影响而产生变形，在τ=0时不再过零点。而由于载波扫频变化，由式(9)可以看出，多径分量的积分结果有sinc函数的形式，因此当积分时间T为sinc函数的零点，即载波扫频范围、扫频周期及多径时延满足2RLΔτT/TL=k,k∈N时，多径分量积分结果为0，从下一节的仿真中可以看出，鉴相函数的变形可以得到抑制。

1.3 相干积分时长内频率变化单调性改变

当载波扫频周期缩短，相干积分时长不再远小于扫频周期时，积分时长T内信号频率的单调性可能发生变化。移动本地复制码片与接收信号进行互相关时，研究R(τ+Δτ)=1时多径分量的积分峰值Mm，假设为t1时刻由线性递增变为线性递减，则有

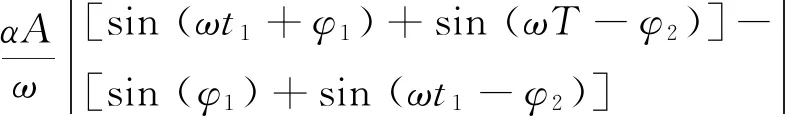
(10)

(11)

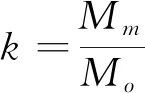
文献[9]证明了BPSK信号码跟踪多径的误差公式，而载波扫频信号只改变了多径分量与本地信号的相位关系，因此可以很容易得出载波扫频信号的多径误差公式为

ε(Δτ,k)=

(12)

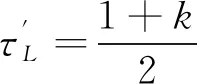
对载频不变的BPSK信号，多径误差的极值出现在Δφ=0或Δφ=π的时刻，而对载波扫频信号，由于相位与扫频周期、扫频范围及多径时延都有关，多径误差的极值与Δφ不再有确定的关系，但仍可通过数值计算得出多径误差包络，将在下一节中给出。

2 仿真与分析

2.1 载波扫频对码相关函数的影响

研究载波扫频对伪码多径分量的相关函数与鉴相函数的影响。假设接收机能够精确跟踪接收信号频率，仿真参数设置如表1。

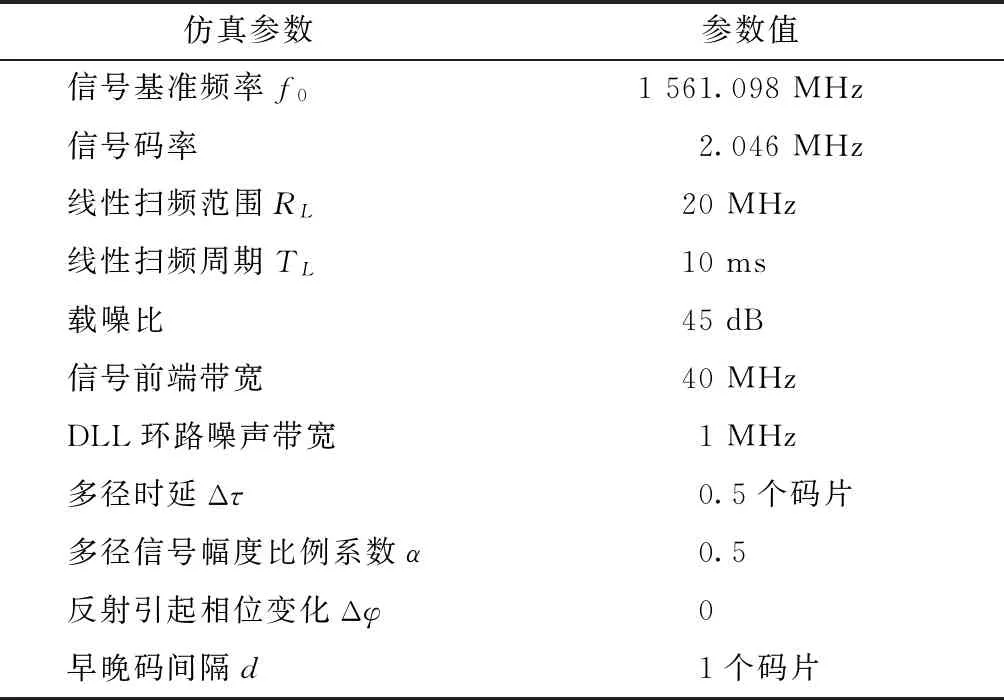
表1 载波扫频仿真参数

当载波线性扫频时，信号解调后伪码的多径分量表现为正弦包络(不考虑噪声)，如图2所示。由式(8)知正弦频率为TL/2RLΔτ=1 ms。积分时长为1个正弦周期，积分结果为0，此时多径分量的相关函数值约为0。

由图3可以看出，多径条件下载频不变的信号码相关函数变形严重，而载波线性扫频的信号相关函数对称性得到改善，虽然受噪声与前端滤波的影响，相关函数仍非理想的对称三角形，但是多径的影响已经得到抑制，相关函数与无多径信号已基本重合。

由图4可以看出，多径信号存在时，传统DLL环路的鉴相函数发生变形，过零点不在τ=0处；而载波扫频信号在同样早晚码间隔的DLL环路下，鉴相函数的变形得到改善，基本与无多径的理想信号鉴相函数重合，多径信号的影响得到抑制。

2.2 扫频周期对多径误差包络的影响

研究伪码多径分量相关函数幅值比例k与扫频周期的关系。考虑线性扫频，对于卫星导航系统，载波扫频范围受到可用频带宽度的限制，因此扫频范围不宜过大，此处设为2 MHz；而文献[10]中提到，对BPSK信号，各场景下的平均多径时延为0.2个码片，因此此处设多径时延为0.2个码片。假设相干积分时长内，频率变化的单调性第一次发生改变的时刻t1为扫频周期的一半，即TL/2，之后每TL/2频率单调性都会发生一次改变。参数计算结果如图5所示。

可以看出，当扫频周期超过10 ms后，幅值比例k逐渐趋近于α，对伪码多径的抑制效果不明显；当扫频周期由10 ms逐渐缩短时，k先是逐渐减小，后又有一定回升；当扫频周期小于相干积分时长1 ms后，随着一个积分时长内频率变化单调性改变次数的不同，k呈现出离散的特性，表2给出了几组不同载波扫频周期下1个码片内的平均幅值比例，总体趋势是扫频周期缩短，幅值比例减小。

表2 平均幅值比例与载波扫频周期的关系

图6给出了载波扫频周期TL=0.1 ms与TL=5 ms时多径误差包络与载波频率不变的BPSK信号在传统DLL环路下多径误差包络的对比。从图中可以看出TL=5 ms时多径误差包络面积有所减小，但并不明显，其包络面积比载频不变信号减小13.4%，而TL=0.1 ms时多径误差包络面积已显著减小97.2%，不同时延的多径误差都能得到较好的抑制。

2.4 仿真结果分析

通过仿真可以看出，仿真结果与理论推导基本相符。当载波线性扫频时，接收机载波剥离后伪码的多径分量有正弦包络的特性，再进行相干积分时，多径分量积分后输出的自相关函数幅值有所下降，多径误差对码环鉴别器的影响也能够得到减轻。

当扫频周期较长、一个相干积分时长内频率变化单调性不发生改变时，相干积分结果表现为sinc函数的形式，sinc函数的零点和相干积分的结果都与扫频周期、扫频范围以及多径时延三者的组合有关，相干积分时长与sinc函数零点越接近，对多径的抑制效果越明显；当扫频周期较短、一个相干积分时长内频率变化单调性多次改变时，相干积分结果与频率单调性变化次数也有关，表现为一定程度的离散特性，但对多径的抑制效果总体随着扫频周期缩短而提升。

3 结束语

GEO卫星是BDS空间星座十分重要的组成部分，对提供高精导航定位服务有重要意义。然而GEO卫星由于其轨道相对地面静止的特点，存在静态多径现象，难以通过传统的多径处理方法进行抑制，同样的情况也存在于WAAS等卫星导航辅助系统及其他地球同步轨道卫星系统之中。

本文分析了载波扫频信号对直接序列扩频伪随机码相关鉴别器的影响，研究了该方法的多径抑制性能。理论推导与仿真结果表明，当载波扫频范围、扫频周期、多径时延三者的组合满足一定条件时，多径分量的相关函数峰值将得到显著抑制，多径信号的影响几乎能够被消除。本文还分析了载波扫频参数对多径抑制性能的影响，扫频范围一定的情况下多径抑制性能总体随扫频周期缩短而提升，但仍表现为一定的离散特性。

理论上，该方法不需要额外的相关器，对接收机也没有大的计算负担，有利于保证接收机导航定位结果的实时性。但是卫星导航系统受限于其频带宽度，扫频范围十分有限；另一方面，载波扫频也增大了动态接收机接收信号多普勒频移的阶数。因此如何选取合适的扫频周期与扫频范围，以及如何保证接收机对载波扫频信号的捕获与跟踪还需要进一步的研究。

[1] KAPLAN E D.GPS原理与应用[M].2版.寇艳红，译.北京：电子工业出版社，2007：157-159.

[2] TOWNSEND B, FENTON P. A practical approach to the reduction of pseudorange multipath errors in a L1 GPS receiver[EB/OL].(2014-10-09)[2017-01-18].https://www.novatel.com/assets/Documents/Papers/File24.pdf.

[3] FAN T, LIN V S, WANG G H, et al. Study of signal combining methodologies for future GPS flexible navigation payload (Part II)[C]//Institute of Electrical and Electronic Engineers(IEEE).Proceedings of Position, Location and Navigation Symposium (IEEE/ION 2008). California:IEEE, 2008: 1079-1089.

[4] SERCRETAN H, MERCIER F, TRILLES S, et al. Robust EGNOS GEO ranging with electric propulsion satellite[C]//The Institute of Navigation(ION).Proceedings of the 27th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2014). Tampa, Florida: ION,2014: 3323-3330.

[5] ZHANG F, HE H, TANG B, et al. Analysis of signal characteristic and positioning performance affected by pseudorange multipath for COMPASS[C]//China Satellite Navigation Conference (CSNC) .Proceedings of China Satellite Navigation Conference (CSNC) 2013. Heidelberg, Berlin: Springer，2013: 493-503.

[6] WEINBACH U, RAZIQ N, COLLIER P. Mitigation of periodic GPS multipath errors using a normalised least mean square adaptive filter[J]. Journal of Spatial Science, 2009, 54(1): 1-13.

[7] XU C T, TANG X M, HUANG Y B, et al. Signal carrier frequency variation approach for GEO satellite multipath mitigation in the BDS[J]. IEICE Transactions on Communications, 2016, 99(11): 2458-2468.

[8] AGARWAL N, BASCH J, BECKMANN P, et al. Algorithms for GPS operation indoors and downtown[J]. GPS solutions, 2002, 6(3): 149-160.

[8] AGARWAL N，BASCH J，BECKMANN P，et al.Algorithms for GPS operation indoors and downtown[J].GPS solutions，2002，6(3)：149-160.

[9] 张孟阳，吕保维.GPS 系统中的多径效应分析[J].电子学报，1998，26(3)：10-14.

[10] 徐成涛.基于统计模型的多径误差评估和现代导航信号多径抑制技术研究[D].长沙：国防科学技术大学，2016：89-90.

A multipath mitigation method based on carrier frequency sweeping for satellite navigation signal

XIEYuchen，XUChengtao，TANGXiaomei，WANGFeixue

(Satellite Navigation R&D Center，National University of Defense Technology，Changsha 410073，China)

In this article，we proposed a method for the situation of static multipath，that is，the multipath of GEO (Geosynchronous Earth Orbit)satellite cannot be mitigated by traditional methods such as average because of their static orbit.By combining sweeping frequency carrier and direct sequence spread spectrum signal，it can be proved that when we sweep the carrier frequency in linear mode，the multipath component of pseudo random code will be contained in a sine wave after carrier demodulation，which can be well mitigated by correlation of code correlator.Besides，we also analyze the parameters of frequency sweeping，which may be constructive for the design of this kind of carrier.

static multipath；pseudo random code；frequency sweeping；code correlation

2017-02-16

谢郁辰(1993—)，男，福建龙岩人，硕士研究生，研究方向为卫星导航信号多径处理。

王飞雪(1971—)，男，福建龙岩人，博士，教授，博士生导师，主要从事星基导航与定位、扩频信号处理全数字接收机领域的研究。

谢郁辰，徐成涛，唐小妹，等.一种载波扫频的伪随机码多径抑制方法[J].导航定位学报，2017，5(3)：38-43.(XIE Yuchen，XU Chengtao，TANG Xiaomei，et al.A multipath mitigation method based on carrier frequency sweeping for satellite navigation signal[J].Journal of Navigation and Positioning，2017，5(3)：38-43.)

10.16547/j.cnki.10-1096.20170309.

U666.1

A

2095-4999(2017)03-0038-06