子结构法在快速解析复杂频率响应模型中的应用＊

张焰 马峰 宋俊 任超

（广州汽车集团股份有限公司汽车工程研究院，广州 511434）

子结构法在快速解析复杂频率响应模型中的应用＊

张焰 马峰 宋俊 任超

（广州汽车集团股份有限公司汽车工程研究院，广州 511434）

结合子结构建模理论，提出了子结构频率响应分析方法，快速求解频率响应模型。通过对比简支梁振动特性的理论解析解、传统频率响应数值解与子结构频率响应数值解，验证了子结构法的准确性。针对某车型后悬置安装点的噪声传递函数140～160 Hz的峰值问题，应用子结构分析方法提出优化前副车架方案，对比传统频率响应分析方法，仿真计算效率提升了94%，仿真与试验结果表明，车内声响应在140～160 Hz内峰值下降了8～10 dB（A）。

1 前言

子结构分析方法结合了“先局部再整体”的思想，将整体结构分割成若干个计算量较小的子结构，对每个子结构进行动力学计算，保留各子结构的传递函数矩阵，而后根据各子结构之间的连接关系，对整体结构的动力学响应进行快速求解与运算，节约了大量的分析计算时间。

子结构分析方法的优越性吸引了众多学者的关注，但多是基于简单模型进行动力学振动特性的分析与研究。吴仕超[1]等以常见的空间桁架结构为研究对象，在频域范围内通过有限元仿真算例验证了子结构理论方法的有效性和可靠性。王雪仁[2]等发展了一种子结构方法，应用于圆柱壳模型的振动特性研究，验证了发展的子结构方法的正确性，并实现了各子结构的独立求解，在各子结构振动特性已知的情况下可快速求解整体结构的振动特性，对比传统有限元法，子结构方法计算效率优势明显。周素霞[3]等引入超单元，利用子结构法建立了一个重载凹底平车底架的弹性体有限元模型，并对比了传统有限元模型的模态结果，前8阶模态误差均在1%以内，验证了子结构法的计算精度与可靠性。

本文基于子结构建模理论[4]，借用有限元分析工具提出子结构频率响应分析方法，并利用简支梁模型与某车型复杂的NVH仿真分析模型验证了该方法的可行性与准确性。同时，替换改进后的前副车架结构模型，优化了后悬置安装点的噪声传递函数峰值问题。

2 子结构频率响应函数

总结构S由子结构M和子结构N构成，分解示意如图1所示。子结构M为（a+c）自由度系统，子结构N为（b+c）自由度系统，M和N连接界面自由度为c。

图1 子结构示意

稳态频率响应运动方程是[5]：

式中，ω为激励频率；M为系统的质量矩阵；i为虚数单位；B为系统的阻尼矩阵；K为系统的刚度矩阵；X为系统结构的位移响应；Z为系统的动态刚度矩阵；F为系统外部激励。

求解上述方程位移响应：

证明如下：假设存在一个概率多项式的主动敌手B，冒充Bob与Alice进行通信。B已获取Alice的与交易相关的随机数tA，并从公开信道上截获了WB。现假定Alice交互过程中选取的随机数为wA=φ，Bob选取的与交易相关的随机数为tB=φ。给定一个计算型Diffie-Hellman问题(gφ,gφ,gφφ)，假定敌手 B 能成功计算K，由可 得则困难问题CDH可解，与实际矛盾。故会话密钥不能被成功计算，此协议可以提供会话密钥安全。

式中，H为传递函数矩阵，也称频率响应函数矩阵。

子结构在频域的运动方程表示为：

系统的频率响应函数Hnn是关于激励频率ω的函数。

3 简支梁模型

如图2所示的二维等截面简支梁结构，以固定点为坐标系原点O，简支梁轴向为x方向。梁长L为1 000 mm，圆截面半径r为10 mm，材料弹性模量E=2.1×105MPa，泊松比μ=0.3，密度ρ=7.8×103kg/m3，在梁长L/3处A点沿y轴正向施加单位简谐激振力F，分析频率范围为0～3 000 Hz，引起系统在平面内的振动响应，主要表现为y方向平动。现利用传统频率响应分析方法和子结构频率响应分析方法计算并输出梁上2L/3处B点的振动响应，并与其理论解进行对比验证。

3.1 理论分析方法

应用简支梁的振动运动方程求得B点响应的理论解[6～8]：

式中，A为梁截面面积；ωi为简支梁第i阶模态频率。

图2 简支梁示意

3.2 传统频率响应分析方法

把简支梁离散成100个圆横截面半径r为10 mm的有限元梁单元CBEAM，约束左端点的空间6个自由度，释放右端点x方向自由度，在A点输入0～3 000 Hz的单位简谐力，频率间隔5 Hz，应用传统频率响应分析方法求解B点的位移响应和速度响应，如图3所示。

图3 传统法的简支梁模型

3.3 子结构频率响应分析方法

以B点为界限，将简支梁分成2个子模型。子模型1是长度为2L/3的二维平面的悬臂梁，约束左端点空间的6个自由度，在A点输入0～3 000 Hz的单位简谐力，频率间隔5 Hz；子模型2是长度为L/3的二维平面梁，释放右端点所示坐标系的x方向自由度，如图4所示。

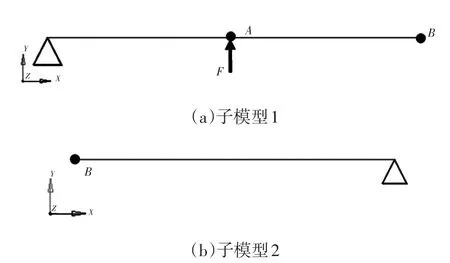
图4 子结构法的简支梁模型

首先，求解子结构1和子结构2的频率响应函数，以矩阵形式单独储存；然后，编写连接文件，对2个子结构的传递点B点进行刚性连接处理，识别B点自由度，进而引用2个子结构的频率响应函数矩阵，求得B点y方向的位移响应和速度响应，如图5所示。对比位移响应与速度响应的理论解析解、传统有限元解和子结构有限元解，峰值频率和幅值基本一致，由此验证了子结构有限元模型的可行性和准确性，可以应用子结构分析方法对复杂结构的频响特性进行深入研究。

图5 B点结构响应

4 整备车身-前副车架NVH模型

以某车型为研究对象，参考李文等提到的白车身简化与建模方法[9]，建立整备车身-前副车架NVH分析模型。应用子结构频率响应分析方法计算整备车身的噪声传递函数矩阵，以及前副车架与车身接附点的振动传递函数矩阵，输出车内声学响应。其中，整备车身子结构与前副车架子结构模型如图6、图7所示。

图6 整备车身子结构

图7 前副车架子结构

4.1 传统频率响应分析方法

装配上述整备车身、声腔和前副车架模型，采用传统频率响应分析方法进行车内噪声的求解，在后悬置安装点Z向施加动态激励（见图7），计算车内20～200 Hz噪声响应特性。图8为后悬置安装点噪声传递函数测试布点。仿真与测试结果见图9。

图8 后悬置安装点噪声传递函数测试

图9 车内噪声仿真与测试结果

4.2 子结构频率响应分析方法

针对整备车身子结构与前副车架子结构，施加与传统频率响应分析同样的边界条件，应用子结构频率响应分析方法进行车内噪声求解，结果见图9。对比传统有限元的车内噪声响应结果和试验测试结果：

a.传统法与子结构法结果曲线一致性高，在20～200 Hz全频范围内，子结构法车内噪声曲线完全保留了传统法分析结果的峰值频率特征，噪声峰值吻合较好，校验了子结构频率响应分析的准确度与可行性。

b.仿真分析后悬置安装点噪声传递函数与测试结果趋势基本一致，且在140～160 Hz均存在明显峰值，验证了仿真模型分析的准确性，可针对实测140～160 Hz噪声传递函数问题进行下一步分析、优化。

4.3 替换前副车架

根据实车测试结果，140～160 Hz幅值最高，是车内噪声贡献的主要频率，故提出了更换前副车架结构的方案，优化的前副车架结构如图10所示。图11是对更换的前副车架进行试验测试。

将优化的前副车架模型替换至原整备车身-前副车架模型，应用传统频率响应分析方法求解车内噪声。由于整备车身结构未作任何修改，而子结构频率响应分析方法保留了整备车身的噪声传递函数矩阵，仅需对更新后的前副车架进行振动传递函数分析，进而组合整备车身子结构噪声传递函数矩阵文件，快速解析更新后模型的车内噪声频率响应曲线，如图12所示。

图10 优化的前副车架

图11 优化副车架的后悬置安装点噪声传递函数测试

图12 优化后的车内噪声

由图12可知：优化后的整备车身-前副车架模型，其车内噪声仿真值和试验值在140～160 Hz范围内峰值下降明显，频段内分别下降8 dB（A）和10 dB（A）。

5 解析效率

整备车身-前副车架NVH分析模型所需求解自由度个数约1 500万，应用传统频率响应分析方法提交至工作站计算，耗时约4 h。利用子结构频率响应分析方法对加速噪声NVH分析模型进行求解共耗时2.74 h。

在整备车身-前副车架NVH分析模型中应用子结构频率响应分析方法，计算效率显著提高。对于前副车架结构的替换，计算效率更加凸显：原子结构分析模型保留了整备车身的噪声传递函数矩阵文件，则仅需对修改后的前副车架子结构进行频率响应函数分析，再结合各子结构的传递函数矩阵，进行频率响应分析，总计耗时约15 min，与传统有限元频率响应分析方法相比计算效率大幅提升。

6 结束语

本文对比简支梁频率响应的理论解析解、传统有限元解和子结构有限元解，三者结果一致，验证了子结构法的准确性和可行性；应用子结构法，提出了前副车架改进方案，改善了后悬置安装点噪声传递函数140～160 Hz峰值问题。仿真与试验结果表明，车内声响应在140～160 Hz内峰值下降8～10 dB（A）。与此同时，相比传统频率响应分析方法，子结构法计算效率明显提升。

1 吴仕超.频域子结构法的实验研究：[学位论文].上海：上海交通大学，2011.

2 王雪仁，缪旭弘，贾地.子结构方法在圆柱壳体振动特性分析中的应用研究.中国舰船研究，2009，4（5）：8～13.

3 周素霞，谢云叶，谢基龙，等.基于子结构法的重载凹底平车底架的固有动态特征分析.铁道学报，2011，8（33）：28～32.

4 Wyckaert K,Xu K Q,Mas P.The virtues of static and dynamic compensations for FRF based substructuring.Spie International Society for Optical，San Diego，1997.

5 Hashash Y M A,Park D.Viscous damping formulation and high frequency motion propagation in non-linear site response analysis.Soil Dynamics and Earthquake Engineering，2002，22（7）：611～624.

6 于德介，程军圣，杨宇.机械振动学.长沙：湖南大学出版社，2010.

7 张义民.机械振动.北京：清华大学出版社，2007.

8 张焰.基于有限元功率流的整车振动与噪声分析：[学位论文].武汉：武汉理工大学，2015.

9 李文，李猛，金永磊，等.轿车白车身试验模态与计算模态相关性分析.汽车技术，2011（6）：34～38.

（责任编辑 斛 畔）

修改稿收到日期为2017年5月11日。

Application of Substructure Method in the Model of Complicated Frequency Response for Rapid Analysis

Zhang Yan,Ma Feng,Song Jun,Ren Chao
（Automotive Engineering Institute,Guangzhou Automobile Group Co.,Ltd,Guangzhou 511434）

Based on the substructure modeling theory,this paper proposed the substructure frequency response analysis method,which can quickly solve frequency response model.By comparing the theoretical analytical solution,numerical solution of traditional frequency response as well as numerical solution of structural frequency response,correctness of this substructure method was verified.For the peak value of 140～160 Hz of noise transfer function at the rear suspension mounting point of a vehicle,substructure analytical method was applied to propose the front frame optimization solution.Compared with traditional frequency response analytical method,efficiency of simulation calculation was improved by 94%.The simulation and test results show that interior acoustic response is reduced by 8 to 10 dB(A)in the peak frequency of 140 to 160 Hz.

Substructure,Simply-supported beam,Front subframe,Transfer function

子结构 简支梁 前副车架 传递函数

U462.3 文献标识码：A 文章编号：1000-3703（2017）08-0059-04

广东省产学研结合项目（2013B09040002）；广东省引进创新科研团队专项（201001N0104818165）。