基于曲率与车速的两点智能控制驾驶员模型＊

杨浩黄江李正网李攀韩中海

（1.重庆理工大学，汽车零部件制造及检测技术教育部重点实验室，重庆 400054；2.重庆人文科技学院，重庆 401524）

基于曲率与车速的两点智能控制驾驶员模型＊

杨浩1黄江1李正网2李攀1韩中海1

（1.重庆理工大学，汽车零部件制造及检测技术教育部重点实验室，重庆 400054；2.重庆人文科技学院，重庆 401524）

为了提高驾驶员模型的路径跟踪精度，基于模糊逻辑智能控制器建立了一种依据道路曲率、车速，采用远、近两点预瞄的智能驾驶员模型。该模型根据目标道路的曲率自适应地选择预瞄距离远、近两点，根据不同的车速和预瞄点的横向偏差决策出最优转向盘转角。对所建立的驾驶员模型与CarSim驾驶员模型进行仿真测试对比，结果表明，该模型能够在反应滞后的情况下完成复杂道路、极限工况的驾驶员操作，路径跟踪误差较CarSim模型小。

1 前言

大多数交通事故是由驾驶员操纵不当和车辆失稳造成的，因而驾驶员模型成为近几年研究的热点领域。目前，驾驶员模型主要有交叉频率模型[1]、最优预瞄控制模型[2]、预瞄最优曲率模型[3]、神经网络模型[4]和模糊模型[5]。由于驾驶员注意力分配问题和反应滞后因素[3]，驾驶员模型的路径跟踪会出现较大误差，因此前三者具有拟线性的驾驶员模型不能用于精确描述驾驶员的非线性行为。神经网络虽然适用于非线性，但需要大量的数据作为训练样本，这给研究造成了一定难度。模糊逻辑控制器基于专家经验设计[6]，不需要精确的数学模型和样本数据，能很好地适用于非线性系统，采用模糊逻辑控制的驾驶员模型在一定程度上能反映人的思维和驾驶行为[7]，因此，本文基于郭孔辉院士提出的“预瞄最优曲率驾驶员模型”，结合模糊逻辑控制器建立了一种基于道路曲率、车速与两点预瞄的智能控制驾驶员模型。

2 最优预瞄控制模型

MacAdam在驾驶员模型建模中结合最优控制理论，提出了最优预瞄控制模型[2]。此模型主要使车辆实际路径与期望路径的横向误差平方和最小，取得了高精度的路径跟踪效果。

该模型得到的最优转向盘转角[8]为：

式中，δs(t)为输入转角；ε(t+Tp)为响应误差；g(Tp)为传递函数；Tp为驾驶员预瞄时间。

由式（1）可知，最优转向盘转角由输入转角、响应的误差和传递函数决定。

3 预瞄最优曲率驾驶员模型

郭孔辉院士提出了“预瞄—跟随理论”[3]，本文在此基础上建立了预瞄最优曲率驾驶员模型。该模型根据车辆实际行驶的横向位移与理想的期望道路横向位移的误差决策出最优转向盘转角，使车辆具有较好的路径跟踪精度。

为了保证车辆转向时车轮均作纯滚动，所有车轮的轴线须相交于一点，即转向中心。对于两轴汽车，内转向轮偏转角δ2应大于外转向轮偏转角δ1。将车轮视为刚体（忽略轮胎的弹性变形），车辆的最小转弯半径为：

车辆实际行驶过程中，转弯半径可近似表示为：

式中，L为轴距；δmax为最大外转向轮偏转角；δ为转向轮转角的均值。

从实际行驶工况来看，车辆绝大多数情况下都行驶在小曲率的道路上，车轮的转角小，sinδ可近似为δ，由式（3）可得道路曲率的通式：

车辆的横向加速度为：

式中，δsw为转向盘转角；i为转向系传动比；v为车速。

由上述分析可知，驾驶员很容易掌握道路曲率与转向盘转角的正比关系，视线预瞄到前方一定曲率的道路时，及时转动转向盘跟随路径。

假设车辆跟随的轨迹中心线横向位移方程为f(t)，如图1所示，并设在所研究的t时刻，车辆的瞬时横向位移为y=y(t)，横向速度为y′=y′(t)。此时驾驶员向前预瞄的距离为d，相应的预瞄时间T=d/v，驾驶员预瞄点的横向位移为f(t+T)。此时道路的曲率为1/R，驾驶员选择转向盘转角δsw来跟踪期望路径，汽车的横向加速度为y″(t)。（t+T）时刻车辆的横向位移为：

根据最小误差原理，驾驶员总会用一个最优的转向盘转角δ*sw来决策出一个最优的轨迹曲率1/R*，使汽车行驶距离d（经过时间T）之后，其横向位置y(t+T)与该处的预期轨迹坐标f(t+T)相一致。在轨迹曲率不大的情况下，由式（6）可得最优横向加速度为：

图1 预瞄最优曲率驾驶员模型

最优轨迹曲率为：

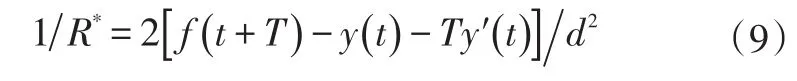
由式（4）可得最优转向盘转角为：

低速工况下驾驶员与车辆的闭环控制系统如图2所示。考虑到实际操作中驾驶员不可避免地存在神经反应滞后和操纵滞后效应，上述驾驶员模型用一个环节“I”来代替理想转向盘转角到实际转向盘转角的传递，，其中e-tds用于考虑神经反应滞后因素，一般取反应滞后时间td=0.1 s[3]，用一阶惯性环节-1/(1+Ths)来考虑驾驶员的反应滞后因素，一般取操纵滞后时间Th=0.2 s[3]。因此如果忽略以上滞后因素，实际转向盘转角与理想转向盘转角相等，这样根据式（9）确定最优轨迹曲率1/R*，并参考车辆转向系传动比i和轴距L确定最优转向盘转角δ*sw，驾驶员以此操纵车辆。

图2 低速时驾驶员-汽车闭环系统

4 基于曲率与车速的两点智能控制驾驶员模型

基于郭孔辉院士的预瞄理论，该模型首先预瞄前方道路远、近2个点，根据生理、心理学家Land和Horwood对驾驶员在弯道行驶的行为研究[9～10]表明：驾驶员在驾驶车辆时，视线集中的范围主要包括“远”（车前方10～20 m）、“近”（车前方6～8 m）2个区域。因此，选择远点预瞄距离为15 m，近点预瞄距离为8 m，远点主要用于车辆在曲率较小的路径行驶，近点主要用于车辆在曲率较大的路径行驶。驾驶员在实际路径跟踪时，对较小曲率的路径，总会把目光距离放远，以更好地跟随路径，反之，对较大曲率的路径，驾驶员总会把目光距离放近，以顺利通过弯道。因此，远、近两点的预瞄模型与驾驶员的实际驾驶行为是一致的。

参考城市道路交叉口转弯半径按道路红线（道路用地的边界线）计，主干道的范围为20～30 m，取其均值25 m作为参考值，其道路曲率0.04作为参考值，取其1/4值0.01作为小曲率来考虑。当道路传感器探测到目标道路曲率小于0.01时，该模型自适应选择远点预瞄，反之，该模型则自适应选择近点预瞄。模糊逻辑控制器根据预瞄点的横向误差和当前的车速，通过模糊规则控制转向盘转角的输出。由于驾驶员的反应滞后和车辆的非线性因素不可避免，要建立精确的人-车-路闭环系统模型是很难实现的，而模糊逻辑控制器能很好地适用于非线性系统，不需要精确的数学模型，因此，将模糊逻辑控制器用于调节预瞄驾驶员的轨迹误差，同时考虑了车速可变对人-车-路闭环系统的影响，使所建立的模型更符合真实的人-车-路闭环系统。图3给出了基于曲率与车速（模糊控制器的车速论域）的两点智能控制驾驶员模型结构框图。其中，误差为经过预瞄时间T，预瞄轨迹和车辆轨迹的横向位移之差，即e=f(t+T)-y(t)-Ty′(t)，模糊逻辑控制器用于提高轨迹跟踪精度，降低汽车转向的振荡。

图3 基于曲率与车速的两点智能控制驾驶员模型结构框图

图4所示为模糊控制器的结构流程图，其中，模糊化过程分两部分。第一部分将所选择的控制变量作为模糊控制器的语言变量。本文对模糊控制器的输入（误差e）定义了7个语言变量，分别是负大（NB）为-5～-3 m、负中（NM）为-4～-2 m、负小（NS）为-3～-1m、零（ZE）为-1～1m、正小（PS）为0～3 m、正中（PM）为2～4 m、正大（PB）为3～5 m；对车速定义了4个语言变量，分别是负零（NZ）为0～60 km/h、零（ZE）为50～70 km/h、正零（PZ）为60～80 km/h、正大（PB）为80～120 km/h；对模糊控制器的输出（转向盘实际转角）定义了8个语言变量，分别是负大（NB）为-50°～-30°、负中（NM）为-40°～-20°、负小（NS）为-30°～-10°、负零（ZE）为-20°～0°、正零（ZM）为 -10°～10°、正 小（PS）为 0°～20°、正中（PM）为10°～30°、正大（PB）为20°～40°。第二部分定义模糊控制器输入和输出变量的论域，然后对整个论域进行模糊分割并给出相应的隶属度函数，隶属度函数选择三角函数。对输入变量e论域的选择，本文参考CarSim软件“8”字形道路和双移线道路，道路实际宽度10 m，所以选择预瞄点到道路中心线的误差为±5 m，当误差的绝对值大于5 m时，模糊逻辑控制器按正大（PB）和负大（NB）来控制，因此e的论域为-5～5 m；由于我国高速公路的最高车速为120 km/h，因此车速v的论域为0～120 km/h。实际行驶中，通常不会在曲率较大的弯道高速行驶，因此选择车速0～80 km/h来仿真大曲率“8”字形道路，并用负零（NS）来考虑0～60 km/h较小车速的影响、用零（ZE）来考虑50～70 km/h一般车速的影响、用正零（PZ）来考虑60～80 km/h较高车速的影响、用正大（PB）来考虑80～120 km/h高速的影响。输出转向盘转角δ论域为-140°～140°，将此论域转化为-40°～40°并用3.5倍增益放大到同等论域，这样有利于将论域整数划分。这样可以得到28条模糊条件语句构成的控制规则，将这些规则组合在一起可以形成模糊规则表，见表1。图5所示为横向误差、车速、转向盘转角的隶属度函数。

图4 基于曲率与车速的模糊逻辑控制器结构

表1 模糊控制规则

图5 隶属度函数

5 仿真试验

为了检验上述驾驶员模型的有效性，基于CarSim和Simulink联合仿真平台对驾驶员转向建模仿真。模型主要应用MacAdam的最优预瞄理论及其最新成果[11]，利用误差积分作为反馈校正（见Error Area）模块，如图6所示。

图6 CarSim模型仿真结构

基于曲率与车速的两点智能控制驾驶员模型与CarSim不同，该模型根据目标道路的曲率，自适应地选择远、近预瞄点。其预瞄点的横向位移误差和不同车速作为输入参考量，同时考虑了驾驶员的反应滞后对人-车-路闭环系统的影响，根据模糊规则决策最优转向盘转角，其结构框图如图7所示（其中车辆的输出分别为预瞄远点、目标道路曲率、预瞄近点、车速，车辆的输入为转向盘转角）。仿真中与汽车有关的参数取自CarSim软件中包含的实际参数，见表2。模型中，用Switch结构进行曲率判断，利用误差和车速通过模糊控制决策出最优转向盘转角，最后通过适当滞后环节形成闭环控制。

图7 基于曲率与车速的两点智能控制驾驶员模型仿真结构

为验证本文设计的驾驶员模型对路径跟踪的有效性，选择了“8”字形和双移线道路对两种驾驶员模型进行对比。“8”字形道路曲率较大，主要用于考虑车辆在急转弯时的路径跟踪精度，由于驾驶员在曲率较大的转弯工况下，通常会降低速度使车辆顺利通过弯道，因此“8”字形道路车辆速度的变化范围设定为0～80 km/h。双移线试验可视为对超车动作的仿真试验，也是包括驾驶员特性在内的“闭环试验”，在一定程度上表现出汽车转向运动的综合能力。由于双移线试验模拟的是驾驶员在真实的道路上的行车过程，有转弯、超车、直线行驶等多种工况，车速的变化范围大，因此将车速范围设定为0～120 km/h。

表2 车辆仿真参数表

“8”字形道路试验结果如图8所示。由图8可知，使用基于曲率与车速的两点智能控制驾驶员模型和CarSim模型的车辆均具有较高的路径跟踪精度，前者在前20 s的横向位移误差只有±0.2 m，后20 s由于车速较高误差有所增大。而后者的横向位移误差为-0.8～0.6 m，在整个路径跟踪过程中，前者的误差均值为0.143 m，后者为0.281 m，表明前者能很好适应曲率较大的路面，车辆急转弯能力强，路径跟踪一致性较后者好，误差更小。

图8“8”字形道路试验结果

双移线道路试验结果如图9所示。由图9可知，使用本文提出的驾驶员模型的车辆路径跟踪轨迹更趋近目标路径，横向位移误差为-0.3～0.2 m，均值为0.025 m，使用CarSim模型的车辆横向位移误差为±0.6 m，均值为0.085 m，表明前者路径跟踪精度高，跟随效果好。

图9 双移线道路试验结果

6 结束语

本文建立了一种依据道路曲率、车速，采用远、近两点预瞄的智能驾驶员模型，可根据目标道路曲率自适应地选择预瞄距离不同的远、近两点进行预瞄，根据不同的车速和预瞄点的横向误差，通过模糊逻辑控制器来决策出最优的方向盘转角。所建立的模糊逻辑控制器能很好地适用于非线性系统，能更加逼近真实的驾驶员行为，可以在复杂道路、极限工况的情况下完成驾驶任务。与CarSim模型相比，本文建立的模型在双移线道路和“8”字形道路跟踪精度都较好，表明该模型不仅能适应曲率较大的弯道，同时路径跟随效果也更好。

1 McRuer D T,Allen R W,Weir D H,et al.New results in driver steering control models.Human Factors，1997，19（4）：381～397.

2 MacAdam C C.Application of an optimal preview control for simulation of closed-loop automobile driving.Transactions on Systems,Man,and Cybernetics，2007，11（6）：393～399.

3 郭孔辉.汽车操纵动力学原理.南京：江苏科学技术出版社，2011.

4 郭孔辉，潘峰，马凤军.预瞄优化神经网络驾驶员模型.机械工程学报.2003，39（1）：26～29.

5 尹晓丽，李雷，贾新春.无人驾驶汽车路径跟踪模糊预测控制.中北大学学报，2011，32（2）：136～138.

6 彭忆强.汽车电子及控制技术基础.北京：机械工业出版社，2014.

7 Kageyama I,Pacejka H B.On a new driver model with fuzzy control.Vehicle System Dynamics，1992，20（sup1）：314～324.

8 MacAdam C C.Understanding and modeling the human driver.Vehicle System Dynamics，2003，40（1-3）：101～134.

9 Land M F,Lee D N,Where we look when we steer.Nature，1994，369（6483）：742～744.

10 Land M,Horwood J.Which parts of the road guide steering?.Nature，1995，377（6547）：339～341.

11 张慧豫.采用远近两点预瞄的新型驾驶员转向模型研究：[学位论文].南京：南京航空航天大学，2012.

（责任编辑 斛 畔）

修改稿收到日期为2017年5月20日。

Two Point Intelligent Control Driver Model Based on Curvature and Speed

Yang Hao1,Huang Jiang1,Li Zhengwang2,Li Pan1,Han Zhonghai1
（1.Key Lab of Automobile Components and Parts Manufacturing and Test Technology of Ministry of Education,Chongqing University of Technology,Chongqing 400054;2.Chongqing College of Humanities,Chongqing 401524）

In order to improve the path tracking accuracy of the driver model,an intelligent driver model was established using fuzzy logic controller according to road curvature,vehicle speed,far and near two preview points.The model adaptively selected the far and near two preview points according to the curvature of the target road,and determined the optimal steering wheel angle according to different vehicle speeds and the lateral deviation of the aiming point.The driver model was compared with the CarSim driver model,which showed that the model can perform driver’s operations under the conditions of complicated road and extreme conditions,meanwhile,the path tracking error was smaller than the CarSim model.

Driver model,Road curvature,Far and near two points,Vehicle speed,Fuzzy logic controller

驾驶员模型 道路曲率 远近两点 车速 模糊逻辑控制器

U469.7 文献标识码：A 文章编号：1000-3703（2017）08-0038-05

国家自然科学基金项目（51105136）。