Kuratowski monoids of various orders on lattices
WANG Hongli, WANG Yidong, TAO Depeng, PENG Yanling
(School of Mathematics and Physics,SUST,Suzhou 215009,China)
Kuratowski monoids of various orders on lattices
WANG Hongli, WANG Yidong, TAO Depeng, PENG Yanling*
(School of Mathematics and Physics,SUST,Suzhou 215009,China)
In this paper,we studied the well known Kuratowski monoids on lattices,searching for the Kuratowski monoids with various orders.Different from the usual approaches,we paid special attention to the structure of the closed operators rather than the properties of the lattices.Some concrete Kuratowski monoids with orders strictly less than 14 are presented.
Kuratowski monoid;closed operator;lattice
1 Introduction
In paper[1],Kuratowski presented a result,called the Kuratowski 14-Sets Theory soon after it was discovered:
Let X be a topological space,and let cl and C denote respectively the closure and complementary operators on subsets of X.Then,the actions of all cl,C and their compositions on an A⊂X give out at most 14 distinguish subsets.Moreover,if X is"not too bad",e.g.X=Rnwith the usual Euclidean topology,then there exists A⊂X such that these actions on A produce exactly 14 distinguish subsets.
This theorem looks very simple at the first glance but turns out to be of deep meaning.Many mathematicians have contributed their efforts to such a topic,mainly looking for the conditions for the topology on X with which 14 can be replaced by 12,10,…,2,or determining the order of the semigroup generated by cl and C,called a Kuratowski monoid[2-6].Recently,observing that the power set 2Xof X is a complete complemented lattice(under the including order)and cl and C are nothing else but operators on such a lattice,with some nice properties such as C2=id (the identity operator) and cl is a closing (see below for definitions),mathematicians started to study such a problem in the category of operators on lattices or more meaningful in the mathematical morphology theory[7-8].It was already shown that the Kuratowski theorem holds on general complemented lattices[4].Now,one of the remaining problems is to find the Kuratowski monoid of orders other than 14.
In this article,we will work with the mathematical morphology operators on lattices.Different from other's work,we pay attention mainly on operators other than on lattices.We construct several Kuratowski monoids with different orders.
2 Preliminaries
(L,≤)(or simply L) denotes a lattice.For any{ai|i∈I}⊂L where I is a non-empty index set,∨i∈Iai(or∨{ai|i∈I},or∨aisimply) and ∧i∈Iai(or∧{ai|i∈I},or∧aisimply) denote respectively the least upper-bound and the greatest lower-bound of{ai} (if exist)[9].A lattice is called complete if for any{ai|i∈I}⊂L,∨i∈Iaiand∧i∈Iaiexist.It is easy to see that,in a complete lattice,there exist a maximal element and a minimal element,denoted by 1 and 0 respectively.In a complete lattice we make the convention that∨{ai|i∈Ø}=0 and∧{ai|i∈Ø}=1 where Ø denotes the empty set.
Definition 1 Let L be a lattice and K be a monoid,i.e.a semi-group with identity.K is called a Kuratowski monoid,(K-monoid for brevity) on L if each g∈K determines an operator,denoted still by g,from L→L and
i)g1=g2in K iff g1(a)=g2(a) for all a∈K;
ii)g1g2(a)=g1(g2(a)) for all g1,g2∈G and a∈L;
iii)e(a)=a for all a∈L where e is the identity in K.
Given a K-monoid K on L,for a∈L,we write K(a):={g(a)|g∈K}and
k(K/L):=sup{|K(a)||a∈L}
where|·|denotes the cardinal of sets.In such terms,the Kuratowski 14-sets Theorem can be reformulated as:if L=2Xand K is the monoid generated by cl and C,then k(K/L)≤14.
Definition 2[7]Given a lattice L.An operator γ:L→L is called a closing if it satisfies
i)a≤γ(a) for each a∈L (extensive);
ii)γ2:=γ◦γ=γ (idempotent);
iii)if a≤b,then γ(a)≤γ(b) (increasing).
Examples are as follows:in the power lattice 2Xof a topology space X,the closure operator cl is a closing;similarly in the power lattice 2Xof a linear space X,the convex-hull operator is also a closing.
In the following,we discuss the K-monoids K(γ,C)(on complete complemented lattices L) generated by a closing γ and the complementary operator C,constructing some concrete γ such that|K(γ,C)|<14 and determining k(K(γ,C)/L) as well.
For this purpose,we need also the following definition.
Definition 3[7]Given a complete lattice L,for each a∈L,we define an operator γa:L→L by

It is easy to check that for each a,γais a closing.We call γaa simple closing.
3 Kuratowski-monoids generated by simple closings
In this section,we present some Kuratowski-monoids K generated by simple closings γ,which satisfy k(K/L)<14.
Theorem 1 If L is a complete complemented lattice with|L|≥6,then for each 1 ≠a∈L,we have k(K(γa,C)/L)=4 or 6 and|K(γa,C)|=10.
Proof.Since γais idempotent and C2=e,besides e,C,γa,we need only to consider the alternate products of γaand C.We declare that for each y∈L,
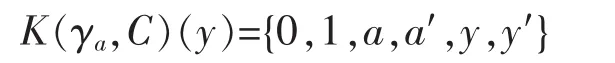
where a′:=C(a).In fact,e(y)=y,C(y)=y′clearly.Now,if y≤a,then
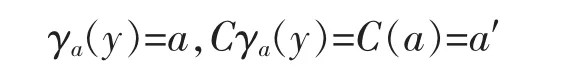


and CγaCγaC(y)=a′=Cγa(y),which also implies that



which leads to,in both cases,

So,the claim is confirmed.Thus|K(γa,C)(y)|=4 (if y=a or a′) or 6 (if not).
Now we see from (1)-(4) that K(γa,C) has most 10 elements:
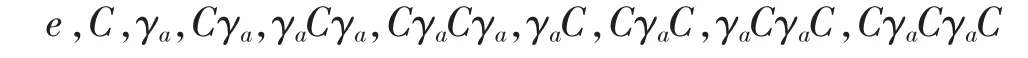
Moreover,e,C,γa,Cγa,γaCγa,CγaCγaare clearly distinct and different from other 4 elements,and as confirmed by taking y∈L such that ya (notice that for any element y other than 0,1,a and a′,one of ya and y′a holds,say ya) and checking the result of action on y,γaC,CγaC,γaCγaC,CγaCγaC are also distinct.Thus|K(γa,C)|=10. □
Theorem 1 can be generalized to little more complicated closings.
Definition 4 Let L be a complete lattice and A:={a1,a2,…,an}⊂L with 0≤an≤…≤a2≤a1≤1.We define an operator γA:L→L by
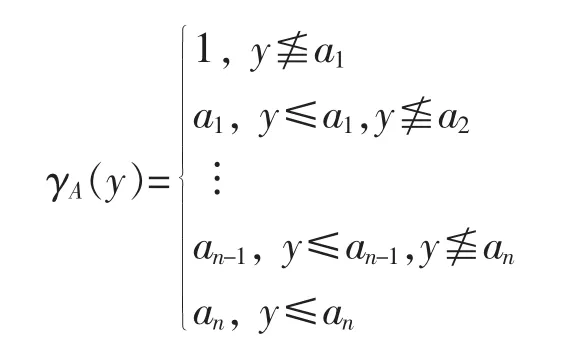
It is not hard to check that γAis a closing.
Theorem 2 If L is a complete complemented lattice with|L|≥8 and A={a1,…,an},then k(K(γA,C)/L)=8(if there is y0∈L such that y0ak+1,y0≤akfor some 1≤k<n) or 6 (if not) and|K(γA,C)|=14 for all n≥2.
Proof. For brevity,we write γ for γAand K for K(γA,C).We declare that

In order to show the claim,we point out first that for each 1≤k≤n,aka1(otherwise,1=ak∨ak′≤a1) and if y≤ak,then y′alfor any l≤n (otherwise,1=y∨y′≤ak∨al<1).Also,by the same reason as in the proof of Theorem 1,we need only to consider the alternate products of γAand C.We will argue in cases.
1oSuppose that y≤an.By an′a1,we get,

which implies a fact(to be used later) that


and γCγCγC(y)=γ(an′)=1=γC(y) which implies a fact that

Thus,1ois confirmed.
2oSuppose yak+1,y≤akfor some 1≤k<n.By aka1,ana1,γ(y)=ak,Cγ(y)=ak′,γCγ(y)=γ(ak′)=1
CγCγ(y)=0,γCγCγ(y)=an,CγCγCγ(y)=an′and

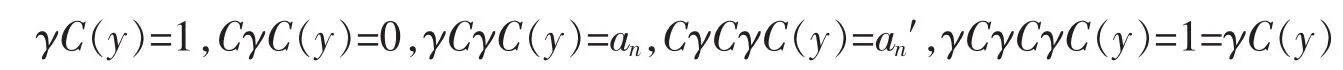
which implies also that

Thus,2ois confirmed.
3oSuppose that ya1.Then,by ana1,
γ(y)=1,Cγ(y)=0,γCγ(y)=γ(0)=an,CγCγ(y)=an′,γCγCγ(y)=1=γ(y)which implies that


(where 1≤k<n)which leads to that,in all cases,

Thus,3ois confirmed.
If there is y0∈L satisfying that y0ak+1,y0≤akor that y0′ak+1,y0′≤akfor some 1≤k≤n,then by 2oor 3o,|K(γA,C)(y0)|=8 and so k(K(γA,C)/L)=8,otherwise,k(K(γA,C)/L)=6.
Now,from (5)-(10),we see that K(γA,C) has at most 14 elements:

Now,e,C,γ,Cγ,γCγ,CγCγ,γCγCγ,CγCγCγ are clearly distinct and different from other 6 elements,and as confirmed by taking k=1 and y=a1′in 3oand checking the result of action on y,γC,CγC,γCγC,CγCγC,γCγCγC,CγCγCγC are distinct as well.So|K(γA,C)|=14.
Remark In this article,we are trying to find Kuratowski-Monoids with different orders in terms of the structure of the closings rather than the properties of the lattices.This is an approach different form any other known ones.However,there are still much more questions left,e.g.what's the condition for the closings under which the orders of the corresponding Kuratowski-monoids are strictly less than 14 etc.We will leave such questions to other papers.At the end,we thank Professor Qi Guo for his discussing with us.
[1]KURATOWSKI C.L'opération A de L'analysis situs[J].Fundamenta Mathematicae,1922,3:182-199.
[2]MOSLEHIAN M S,TAVALLALI N.A generalization of the Kuratowski closure-complement problem[J].Punjab Univ J Math,1995,58:1-9.
[3]LANGFORD E.Problems of Kuratowski type involving unions and intersections[J].Notice Amer Math Soc,1975,22:A-485.
[4]FIFE J H.The Kuratowski closure-complement problem[J].Fundamenta Mathematicae,1991,64(3):180-182.
[5]SHERMAN D.Variations of Kuratowski 14 set theorem[J].American Mathematical Monthly,2004,117(2):113-123.
[6]TASTCB.On the partially ordered monoid generated by the operators H,S,P,P0on classes of algebras[J].J Algebra,2001,245:1-19.
[7]Kiselman C O.Digital Geometry and Mathematical Morphology[EB/OL].[2004-10-06].http://www2.math.uu.se/~kiselman/dgmm2004.pdf.
[8]郭进峰,苏郇立,国起.格上基于膨胀与腐蚀的闭元与开元[J].苏州科技学院学报(自然科学版),2013,30(2):1-6.
[9]GRÄTZER G.General Lattices Theory[M].2th ed.Boston:Birkhänser,2003.
关于格上的Kuratowski幺半群
王泓力,王义东,陶德鹏,彭燕玲*
(苏州科技大学 数理学院,江苏 苏州 215009)
研究一般格上的Kuratowski幺半群,寻找具有不同阶数的Kuratowski幺半群。不同于通常的利用格的特性给出各种阶数的Kuratowski幺半群的方式,文中将利用闭合算子的结构特点构造Kuratowski幺半群。给出了一些具体的阶数严格小于14的Kuratowski幺半群。
Kuratowski幺半群;闭合算子;格
2015-06-11
国家自然科学基金资助项目(11271282);江苏省高校科技创新基金资助项目(201410332059X);苏州科技大学自然科学基金资助项目(2013)
王泓力(1993-),男,江苏常州人,硕士研究生,研究方向:离散数学。
O153MR(2010) Subject Classification:06F05;06B99
A
2096-3289(2017)03-0015-04
责任编辑:谢金春
*通信作者:彭燕玲(1967-),女,博士,教授,硕士生导师,E-mail:yanlingpeng35@hotmail.com。

