基于统计量的加权函数图像重建方法*

乔少华， 李润鑫， 刘 辉， 尚振宏

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

基于统计量的加权函数图像重建方法*

乔少华， 李润鑫， 刘 辉， 尚振宏

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

针对图像重建的问题，提出了一种基于统计量的加权函数图像重建方法。考虑到退化图像不仅含有高斯噪声，且含有拉普拉斯噪声，利用最大似然估计的思想估计高斯噪声和拉普拉斯噪声的方差构造基于统计量的高斯和拉普拉斯权重函数；由于在图像重建过程中，噪声分布发生变化，整合L1，L2范数，设计了一种自适应加权函数；结合双边全变差(BTV)正则化算法，设计了一种自适应加权函数图像恢复方法。实验结果表明：相比基于L1-L2混合误差模型(HEM)，方法的峰值信噪比(PSNR)和结构相似度(SSIM)分别平均提高了约2.07 dB，0.02, 对含有多种噪声的退化图像能够取得比较理想的结果。

统计量； 自适应； 加权函数； 方差； 双边全变差

0 引 言

图像重建是指利用信号处理和图像处理的方法，通过软件计算的方式将退化的低分辨率(LR)图像转化成高分辨率(HR)图像的技术[1～7]。图像重建主要方法有：凸集投影(projection onto convex sets,POCS)方法[8]、迭代反投影(iterative back projection,IBP)方法[9]、最大后验概率(maximum a posteriori,MAP)估计方法[10]和最大似然(maximum likelihood,ML)估计[10]。其中，最大似然估计是基于最大后验概率估计的一种方法，基于概率的算法框架。这类方法较为灵活，特别是它的正则项，可以自由加入对具体问题的具体约束。在提出最大后验概率方法之后，对于如何设计一个有效的正则项成为图像处理领域的研究热点和难点[1]。比较常用的正则化方法有Tikhonov[11]正则项、全变差(total variation,TV)[12]正则项、双边全变差(bilateral total variation,BTV)[13]正则项、Student-t正则化[14]。基于BTV正则化算法能够得到比较理想的稀疏解，同时具有良好的边缘信息保持和平滑效果，本文采用BTV作为正则项。

实际上,许多退化的图像不仅含有高斯噪声，而且含有拉普拉斯噪声，无论选择L1范数模型，还是选择L2范数模型，都不能得到比较理想的重建结果。针对这一问题，SongH H等人[3]提出了一种基于L1-L2混合误差模型(hybird error model,HEM)的超分辨率图像重建算法，由于噪声分布比列发生变化，该模型采用的权重函数不能完整地诠释噪声分布关系，不是最优权重函数，为此，本文设计了一种基于统计量的自适应加权函数。

在图像重建的迭代过程中，噪声分布会发生变化，本文设计的自适应加权函数图像重建方法，利用最大似然估计的思想，通过估计高斯和拉普拉斯噪声方差，构造基于统计量的权重函数，根据噪声分布比例赋予L1，L2范数相应的权重，起到自动加权，并结合双边全变差正则化算法。实验结果表明：本文方法可以有效地去除图像噪声，并且在图像平滑区域、边缘保持等细节方面具有更好的重建效果。

1 方 法

1.1 图像退化

图像退化是指图像在获取、传输和存储的过程中，因各种不确定因素影响导致图像质量的下降。通常，图像退化数学模型可以用一个线性过程来表达，其定义式为

zk=DkHkFkX+Nk,k=1,…,K

(1)

式中X为原始高分辨率图像;z为退化图像;Dk为第k模糊算子；Hk为第k幅图像的下采样算子;Fk为第k幅图像的几何运动算子;Nk为加性噪声。

目前，图像重建均以退化模型式为理论依据，通过已知的LR图像z，对式(1)反向求解，得到HR图像X，与此同时，该求解过程往往忽略一些问题：由于LR图像数量不足以及病态的模糊因子D，往往导致解的不唯一性。为了解决这一系列问题，通常采用正则化方法对其解空间加以限制。加入正则项的代价函数如下

(2)

式中 l通常取1或2; λ为正则参数;Xr为正则项。对式(2)进行最优化求解就可以完成图像的重建。对于Xr，本文选择BTV作为图像重建正则项。

1.2 BTV正则化算法

同时利用空间距离与灰度差值对图像进行重建，图像噪声抑制效果比较明显，还能很好地保持边缘信息。其正则项表达式为

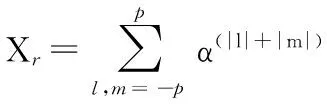
(3)

1.3 加权函数图像重建方法

为了同时兼顾L1，L2范数特点，文献[3]提出了自适应范数HEM，其目标函数如下

(4)

通过观察HEM算法的权重函数，其分布图如图1所示，可知，该权重函数使得两种噪声比例在0～1之间,未完全覆盖，例如,拉普拉斯噪声权重无法取到0.2，即当拉普拉斯噪声权重小于0.3时，对应的权重函数只能取到0.3。

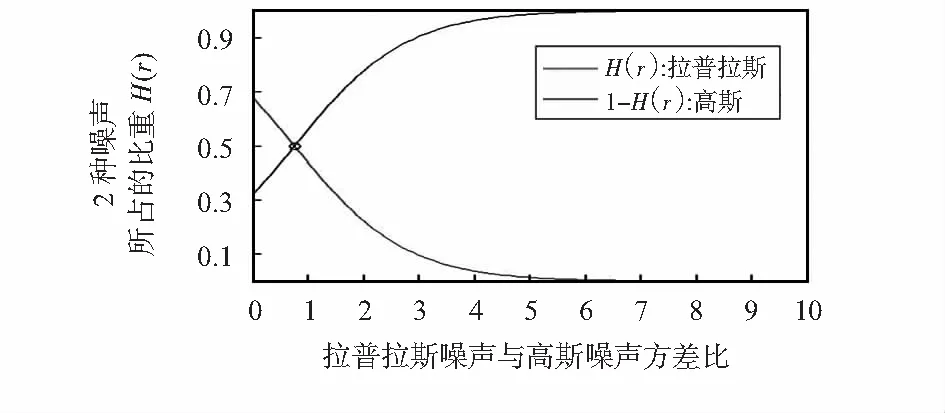
图1 HEM权重函数H(γ)曲线

为了克服这一缺陷，本文考虑利用最大似然估计，构造基于统计量的拉普拉斯权重函数，其定义为

(5)

(6)

同理，高斯权重函数为1-S(v)。

如图2所示，当v=0.5时，高斯噪声和拉普拉斯噪声分布趋于相等；当v≥0.5时，混合噪声偏向于拉普拉斯分布，加权函数自主选择L1范数；当v≤0.5时，混合噪声偏向于高斯分布加权函数自主选择L2范数。相比HEM算法的权重函数，本文方法权重函数的2种噪声分布所占比例全覆盖，即S(v)∈[0,1]，1-S(v)∈[0,1]，而文献[3]的2种噪声分布所占比例分布非全覆盖，即H(γ)∈(0,0.681 4)，1-H(γ)∈(0.318 6,1) 。

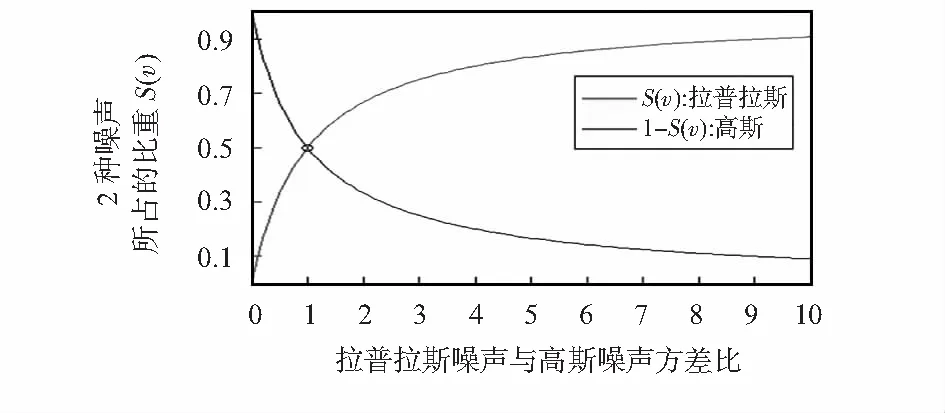
图2 本文方法权重函数曲线S(v)

理论上,图像噪声可以理解为不可预测，随机发生，是一个多维随机过程，因此，可以利用概率密度分布函数描述，则高斯和拉普拉斯的概率密度分布函数定义如下

(7)

(8)

式中r为N维噪声向量;σG，mG，σL和mL分别为高斯和拉普拉斯对应的方差和均值。

计算拉普拉斯概率密度分布函数的最大似然估计(MAP)，对式(8)两边取对数

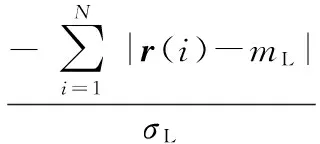
(9)

对式(9)分别求mL和σL的偏导数

(10)

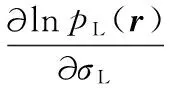
(11)

由式(10)、式(11)计算拉普拉斯的均值和方差

(12)

(13)

同理，可得高斯均值和方差

(14)

(15)

则本文自适应加权函数为

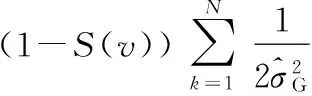
(16)

综合式(3)、式(16)，最终的图像重建目标函数为

(17)

针对式(17)使用标度共轭梯度(scaled conjugate gradient，SCG)优化，在计算过程中，通常要考虑迭代的次数以及连续2次迭代相减的绝对值是否满足给定的阈值。在迭代的过程中，噪声分布比S(v)会发生变化，求取连续2次v相减的绝对值，如果绝对值小于给定的阈值，则终止迭代，否则继续迭代，直到达到所设定的迭代次数为止。通过Matlab平台计算，本文方法在迭代次数将近50时趋于稳定，终止迭代，如图3所示。

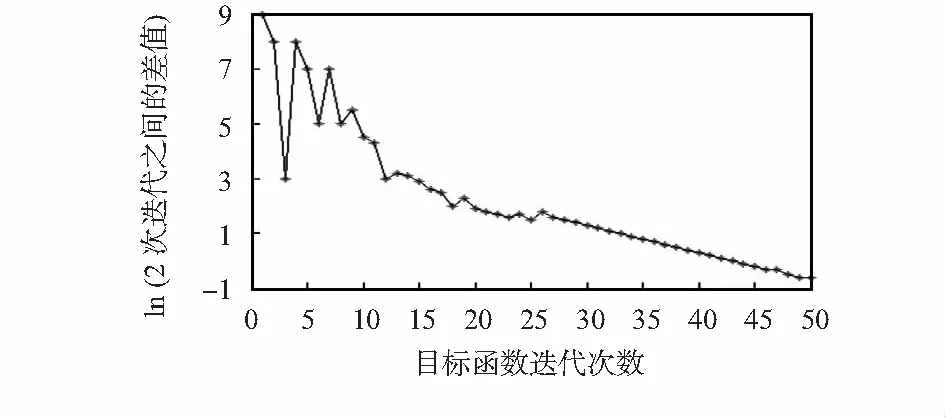
图3 迭代过程

2 实验与分析

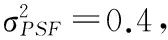
图4 Lena退化图像

利用峰值信噪比(peak signal to noise ratio,PSNR)和结构相似度(structural similarity,SSIM)作为图像重建质量评估标准如下

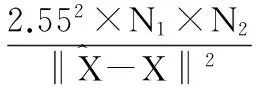
(18)

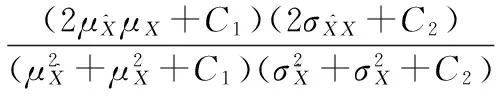
(19)

第一组实验，在退化的Lena图像中添加密度为0.08的拉普拉斯噪声，选择比较常见的椒盐噪声。如图5所示，其中，基于L2BTV算法对拉普拉斯噪声抑制效果不理想，而基于L1BTV的抑制效果相比于L2范数更好，图5(c)较图5(b)的去噪效果好，但是相比于图5(d)，图5(c)有块状效应，图5(d)的去噪效果明显好于图5(c)，比较图5(d)和图5(e)，发现，后者的去噪效果明显好于前者，通过表1发现，相比于HEM，本文方法PSNR提高了1.85dB，SSIM提高了0.02。

第二组实验，在退化的Foreman图像中添加方差为0.1的高斯噪声，如图6所示，对比基于L2范数和L1范数对高斯噪声和拉普拉斯噪声的去噪能力，发现图6(b)去噪效果明显较图6(c)好，而相比于图6(d)，图6(b)有棋盘效应。再比较图6(d)和图6(e)，通过表1发现，相对比HEM，本文方法PSNR提高了2.28dB，SSIM提高了0.02。

3 结 论

本文在HEM算法的基础上，设计了一种基于统计量的加权函数图像重建方法。考虑到在图像重建过程中噪声分布比例发生变化的问题，基于统计量思想与L1，L2范数，设计了一种自适应加权函数,有效地解决了此问题。关于正则项，本文选取BTV正则化算法，实验结果表明：本文方法可以获得比较理想的重建结果。同时，存在以下问题：1)关于正则项算法需要做更深入的研究。2)选取SCG作为目标优化函数，表现出迭代次数偏多。后期将针对以上问题开展研究。

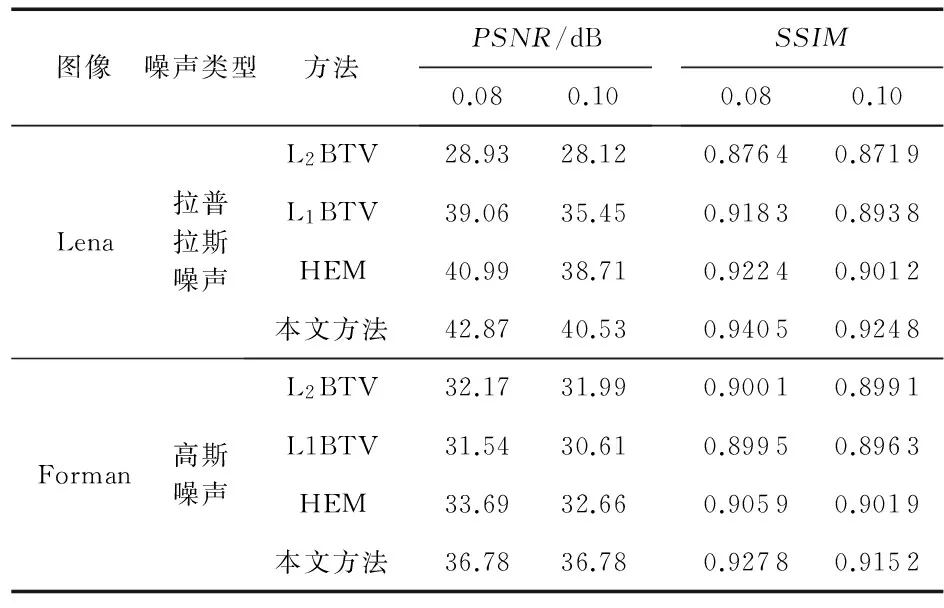
表1 不同算法的PSNR与SSIM值

图5 添加椒盐噪声不同算法重建效果

图6 添加高斯噪声不同算法重建效果

[1] 苏 衡,周 杰,张志浩.超分辨率图像重建方法综述[J].自动化学报,2013,39(8):1202-1213.

[2] 李 佳,张立峰,田 沛.基于Kalman滤波的ECT图像重建算法[J].传感器与微系统,2015,34(8):128-130.

[3] Song H H,Zhang L,Wang P K,et al.An adaptive L1-L2hybrid error model to super-resolution[C]∥Proceedings of 2010 IEEE 17th Interational Conference on Image Processing，Piscataway:IEEE,2010:2821-2824.

[4] 韩 震,王红斌,余正涛,等.双边非局部均值滤波图像去噪算法[J].传感器与微系统,2016,35(6):124-127.

[5] 沈千里,陈 晓,支亚京,等.一种新的人脸图像去噪算法[J].传感器与微系统,2015,34(11):133-136.

[6] 沈 玉，兰瑞田.噪声图像边缘检测中改进Soble算子的仿真实现[J].无线电工程，2014，44(8)：27-30.

[7] 吴晓云，李 华.基于边缘信息改进的线性插值算法研究[J].自动化技术与应用，2016,35(12)：67-69.

[8] Lee E S,Kang M G.Regularized adaptive high-resolution image reconstruction considering inaccurate sub-pixel registration[J].IEEE Transactions on Image Processing,2003,12(7):826-837.

[9] Irani M,Peleg S.Improving resolution by image registration[J].Graphical Models and Image Processing,CVGIP:1991,53(3):231-239.

[10] Feng Zuren,Lu Na,Li Liangfu.Research on image matching similarity criterion based on maximum posterior probability[J].Acta Automatica Sinica,2007,33(1):1-8.

[11] Hennings-yeomans P H,Baker S,Kumar B V K V.Simultaneous super-resolution and feature extraction for recognition of low-resolu-tion faces[C]∥Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition(CVPR),Anchorage,AK:IEEE,2008:1-8.

[12] Rudin L,Osher S,Fatemi E.Nonlinear total variation based noise removal algorithms[J].Physica:D,1992,60:259-268.

[13] Farsiu S,Robinson D,Elad M,et al.Fast and robust multi-frame super-resolution[J].IEEE Transactions on Image Processing,2004,13(10):1327-1344.

[14] Chantas G,Galatsanos N,Likas A,et al.Variational Bayesian image restoration based on a product of distributions image prior[J].IEEE Transactions on Image Processing,2008,17(10):1795-1805.

[15] Patanaviji V,Jitapunkul S.An iterative super-resolution reconstruction of image sequences using fast affine block-based registration with BTV regularization[C]∥2006 IEEE Asia Pacific Conference on Circuits and Systems,APCCAS 2006,IEEE,2006:1717-1720.

李润鑫，通讯作者，E—mail:rxli@kmust.edu.cn。

DOI:10.13873/J.1000—9787(2017)09—0057—04

Study on weighting function image reconstruction method based on statistic*

QIAO Shao-hua, LI Run-xin, LIU Hui, SHANG Zhen-hong

(School of Information Engineering and Automation,Kunming University of Science and Technology,Kunming 650500,China)

Aiming at image reconstruction problem,an image reconstruction method based on weighting function with statistic is proposed.Regarding as degraded images not only have Gaussian noise but also have Laplacian noise ,the idea of the maximum likelihood estimation is adopted to estimate the variance of Gaussian noise and Laplacian noise; Because,in reconstruction process,the distribution of noise change,the weighting function of Gussian and Laplace is constructed based on statistic,which integrates L1and L2norm,and design an adaptive weighting function.Combine with bilateral total variation(BTV) regularization algorithm,an adaptive image restoration method is designed by weighting function.Experimental results show that in comparision with hybrid errors model(HEM) based on L1-L2norm,peak signal to noise ratio(PSNR) and structural similarity(SSIM) are increased by an average of about 2.07 dB,0.02,for degraded image with different noise，can achieve more satisfied result.

statistic; adaptive; weighting function; variance; bilateral total variation

10.13873/J.1000—9787(2017)09—0053—04

2016—09—08

国家自然科学基金资助项目(61462052);云南省人才培养基金资助项目(KKSY201403049)

TP 391

A

1000—9787(2017)09—0053—04

乔少华(1986-)，男，硕士研究生，主要研究方向为图像处理与模式识别。