AOA无源定位最优构型分析*

徐国训， 梁晓龙， 王维佳， 张佳强

(空军工程大学 空管领航学院，陕西 西安 710051)

AOA无源定位最优构型分析*

徐国训， 梁晓龙， 王维佳， 张佳强

(空军工程大学 空管领航学院，陕西 西安 710051)

针对无源定位研究中，传感器—发射机的空间构型对最终的定位估计存在较大影响问题，通过装备无源接收器的接收机运用到达角度(AOA)量测方法对发射机进行定位，计算克拉美罗界(CRB)并分别在距离和分布角度改变的情况下分析最优空间构型，在不考虑接收机约束的情况下给出了接收机—目标最优几何构型的理论分析，得到了目标静态条件下接收机最优空间构型的分析结果，并运用自适应遗传算法(GA)进行了仿真验证。

空间构型； 无源定位； 克拉美罗界； 多传感器协同

0 引 言

传感器无源定位的目的在于通过静态或动态的传感器平台连续追踪信号发射源确定目标位置，广泛应用于无线传感器网络(wireless sensor networks,WSNs)，现阶段使用无源量测方法进行传感器网络定位的研究较多，如无源到达时间差(time difference of arrival,TDOA)定位[1,2]，到达角度(angle of arrival,AOA)定位等，其中AOA目标定位是基于多个接收机的到达角度线为量测基础，现已经成为十分重要的研究领域。

无源定位算法的性能与接收机—目标的相对几何构型相关，文献[3]研究了接收机在单一构型下的目标定位和跟踪问题，但在得到最优构型的同时未考虑定位的不确定性，本文给出了在静态目标下更严格的AOA定位最优构型的理论推导，将计算得到对目标定位的克拉美罗界(Cramer-Rao bound,CRB)和测量值误差协方差作为目标函数评估接收机—目标机最优构型。

1 AOA量测原理

AOA定位原理如图1所示，图中所有的节点坐标方向相同，通过获得通信范围内多个信标节点的坐标和角度信息，再利用位置计算方法计算未知节点位置 。

图1 AOA定位方法示意

2 基于AOA的无源定位问题描述

考虑M架装备无源传感器的接收机执行目标定位任务，其中M个接收机的空间构型如图2所示，第i个接收机的位置为：xi(k)=(xi(k),yi(k))T，设目标位置为xt=(xt,yt)∈R2，ri为第i个接收机到发射源的距离，相邻接收机相对目标连线夹角为φij=φji∈[0,π]。

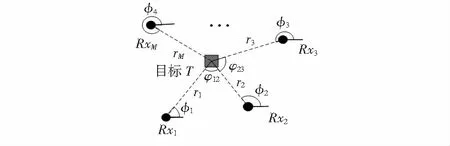
图2 M个接收机的AOA定位构型

φi(xt)=arctan 2(xt-xsi,yt-ysi)

(1)

M个接收机的量测值集合可表示为：i(xt)=φ(xt)+e,其中φ(xt)=[φ1(xt),…,φM(xt)]T，e=[e1,…,eM]T，假定不同接收机的量测误差相互独立，且误差协方差Rφ其中,IN为N维的辨识矩阵为量测方差。

AOA定位的目的是估计目标定位值xt，本文主要对AOA量测方法下接收机—目标最优构型对目标定位和追踪精度的效果进行分析。给出了基于CRB的理论分析结果，在考虑传感器平台无约束的条件下结合理论分析结果，目标定位效能得到了提升。

3 无接收机约束下的最优构型分析

(2)

式中J为Fisher信息矩阵(Fisher information matrix,FIM)，设为M架接收机角度的量测值集合，则FIM中元素可表示为

(3)

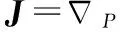
(4)

即FIM可表示为

(5)

为研究方便，FIM的特征值可按下式计算得出

(6)

则CRB可表示为

(7)

任何可以最小化CRB的接收机—目标空间构型均可被称作最优接收机构型，设f(φ,r)为目标函数，则该优化问题可以转换为

(8)

则f(φ,r)为角度φ和距离r的函数，因此，目标函数的解析解可以分别从角度变化和距离变化分析得出。

3.1 角度变化情况分析

设ri,i∈{1,…,N}任意并确定，FIM的最大特征值对应于CRB迹的最小值，则可得到以下最优化问题

(9)

1)当M=2时，式(9)可简化为

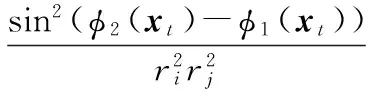
(10)

2)当M=3时，目标函数可表示为

(11)

则由式(11)可得各接收机与目标间连线夹角φ12,φ13和φ23如下

(12)

(13)

式中 “”为集合减除号，在将第M号接收机放置在其他接收机的相反方向上时，量测值的误差协方差最小，此时达到最优。

3)当M≥4时，可以得到如下结论：

a.当距离ri任意并给定时对于所有的接收机i∈{1,…,M>4}，可以得到

(14)

若上式成立，当且仅当

(15)

M≥4时，在式(15)条件下最优接收机构型可能有多个解，使得式(15)的解不够简洁，文献[4]给出了一种将接收机分割为装备有2～3个传感器子群的方法，通过优化子群的传感器分布角度即可得到最优构型。

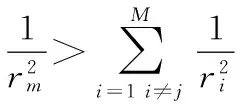
(16)

式(16)中的空间构型为：当其中一个接收机相对目标的距离大于或小于其他传感器平台时，此时的最优构型为将第M架接收机放置在正对其他接收机的方向上，而其他传感器平台分布在同一条直线上。

b.对于接收机距离相等的特殊空间分布情况，即r1=r2=…=rM=r,M≥3时，FIM的约束为

(17)

式(17)成立的条件为

(18)

式(18)对应的2种特殊角度分布的最优空间构型为：

等角分布构型UAA

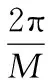
(19)

非等角分布构型(Non-UAA)

(20)

与TDOA定位不同的是，AOA定位不仅在接收机等角分布下可得到传感器最优构型，在非等角分布下同样可得到最优构型[5]。

为直观体现空间构型理论分析结果，计算双机和三机情况下FIM特征值，如图3(a)～(d)所示。

图3 FIM特征值

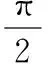
在考虑角度变化情况时，接收机最优角度分布并不唯一，存在接收机非等角分布下的最优构型且受接收机和目标距离r的影响。

3.2 距离变化情况分析

当接收机角度任意并给定时，式(9)所示的目标函数可简化为

(21)

式中 mij=sin2(φj(xt)-φi(xt))任意且连续，则可得到如下结论：当角度φ任意并确定时，接收机与目标的距离越小，则CRB的迹越小。设距离最小值为rmin，则当ri=rmin,i=1,2,…,M时，可得到目标函数f(r)的最大值。

4 仿真验证

运用遗传算法(GA)对上述结论进行仿真验证。遗传算法是基于自然选择和基因遗传学原理的优化搜索方法，本文选择一种实数编码的自适应GA来解决以最大似然估计为目标函数的AOA定位中的搜索问题[6～8]。标准GA存在过早收敛于局部值等缺陷，本文采用在选择前保留最佳个体的蒙特—卡洛选择、算术交叉及非均匀变异，交叉与变异算子可由式(22)、式(23)确定

(22)

(23)

式中fmax为群体中最大适应度值;fa为每代群体的平均适应值;f＇用于交叉的两个个体中较大适应值;f为待变异个体的适应度值;c1,c2,c3,c4在[0,1]内取值。算法的流程如图4所示。

图4 自适应GA流程

上述算法所要解决的问题就是利用自适应GA通过寻优迭代逼近AOA定位的最优构型，使得CRB趋于最小[9,10]，即算法的适应度函数为

f(θ)=arg{min[J-1(ri,θi)]

(24)

图5 无源定位最优构型

5 结束语

给出了静态目标情况下传感器接收机—目标AOA无源定位最优构型的理论分析，分别给出角度和距离变化下AOA无源定位最优构型的解析解，最后运用自适应GA对上述理论分析结果进行了仿真验证，仿真结果表明:该理论推导结果与AOA无源定位最优构型的实际情况吻合，验证了理论分析方法的正确性。

[1]MengW,XieL,XiaoW.OptimalTDOAsensor-pairplacementwithuncertaintyinsourcelocation[J].IEEETransactionsonVehicularTechnology,2016,65(11):9260-9271.

[2]ZhaoS,ChenBM,LeeTH.Optimalplacementofbearing-onlysensorsfortargetlocalization[C]∥2012AmericanControlConference,Canada,2012.

[3] 花 超，吉小军，蔡 萍，等.基于RSSI差分修正的加权质心定位算法[J]．传感器与微系统，2012，31(5) :139-141．

[4]DogancayK,HmamH.OptimalangularsensorseparationforAOAlocalization[J].SignalProcessing,2008,88:1248-1260.

[5] 吕 振，谭鹏立．一种基于RSSI校正的三角形质心定位算法[J]．传感器与微系统，2010，29(5):122-124．

[6] 汪 波，薛 磊.基于遗传算法的TDOA/AOA定位系统的最优布站算法[J].计算机工程与应用，2009,45(24)：219-221.

[7] 倪 巍,王宗欣.基于接收信号强度测量的室内定位算法[J].复旦学报:自然科学版,2004,43(1):72-76.

[8] 周海洋，余 剑，张卫涛基于最小误差平方和的无线传感器网络多边定位算法[J]．传感器与微系统，2014，33(7):126-132．

[9]ShiehChing-sung,LinChin-teng.Avectorneuralnetworkforemitteridentification[J].IEEETransactionsonAntennasandPropagation,2002,50(8):1120-1127.

[10] 常 强，侯洪涛，李 群,等．合作定位节点选择策略[J]．北京：国防科技大学学报，2014，36(5):168-173．

Analysis on the optimal formation configuration of passive localization using AOA*

XU Guo-xun， LIANG Xiao-long， WANG Wei-jia， ZHANG Jia-qiang

(College of Air Traffic Control and Navigation，Air Force Engineering University，Xi’an 710051,China)

In the study of passive localization problem,localization estimation can be seriously influenced by sensors-emitter space.Angle-of-arrival(AOA)measurements are used to locate emitter by configuration with passive receivers.The Cramer-Rao bound(CRB)is calculated and the optimal space configuration is analyzed via changing distance and angular distribution,theoretic analysis of optimal geometry of receiver-target is given without considering receiver constraints.Analytic solutions to the optimal space configuration of receiver are achieved in static cases.Simulation verification is carried out by using self-adaptive genetic algorithm(GA).

space configuration; passive localization; Cramer-Rao bound(CRB); multi-sensor cooperation

TN 97

A

1000—9787(2017)09—0057—04

2017—07—31

国家自然科学基金面上资助项目(61472442，61472443);陕西省自然科学技术研究发展计划资助项目(2013JQ8042，2016JM6071)

徐国训(1992-)，男，硕士研究生，主要研究方向为航空集群理论与技术。