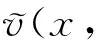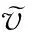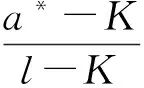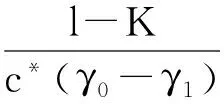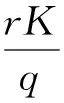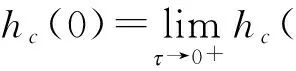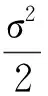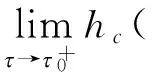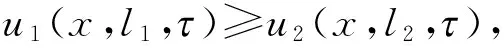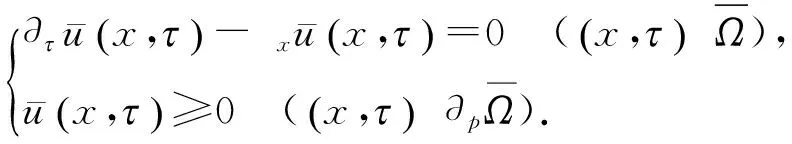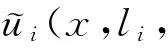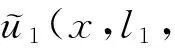一种新型美式期权的自由边界问题
陈晓珊, 曹利敏, 易法槐
(1. 华南师范大学数学科学学院,广州 510631; 2. 廊坊燕京职业技术学院,三河 065200)
一种新型美式期权的自由边界问题
陈晓珊1*, 曹利敏2, 易法槐1
(1. 华南师范大学数学科学学院,广州 510631; 2. 廊坊燕京职业技术学院,三河 065200)
研究一种新类型的股票期权定价问题,当股票市场不利于普通的美式股票期权时,此类期权为持有者提供了一个最低保障. 将该金融问题转化为一个具有2条自由边界的抛物变分不等式,利用偏微分方程理论证明了该问题解的存在唯一性,并且得到2条自由边界的存在性、单调性和光滑性,以及抛物变分不等式的解与最低保障之间的关系.
期权定价; 变分不等式; 自由边界
美式看涨期权是一种未定权益,期权持有者有权在合约规定的到期日以前(包括到期日)任何一个工作日,按确定价格购买一定数量的原生资产,但不承担必须购入的义务,期权的持有者为了取得这个未定权益所需要付出的代价称为期权金[1-4].
现在,许多公司都把股票期权作为奖金奖励给公司的杰出员工. 目前标准的股票期权的主要缺点是期权收益具有很大的不确定性,最主要的不确定性来自股票市场,当整个股票市场的股票价格波动较大时,股票期权就难以逃脱受整个股票市场波动的命运,会给期权的持有者带来畸高或畸低的收入,而与企业的绩效没有多大关系,因此就降低了它对公司员工的吸引力. 而对于公司来说,无力改变市场,所能做的就是构造一种异于普通股票期权的新类型股票期权,使得这种期权对员工有较高的吸引力. 公司在新类型的股票期权合约中确定一个大于敲定价格K的价值保障l,使得期权在t(t≤T)时刻实施时的收益为(max(st,l)-K),其中st是股票的价格,T是到期日. 这种新类型期权相当于在没有改变股票期权的标准形式下,公司给了优秀员工在奖金与股票期权之间一个选择的机会[5].
这种新类型的期权有以下几个优点: 第一,公司的优秀员工得到的奖励有一个最低的保障l-K; 第二,在市场背离本公司的股票的时候,公司不必重新发行股票期权. 这种策略极大地鼓舞了公司的士气,并且避免了由于重新发行股票期权而对公司股本的稀释. 这种期权的一个可能的缺点是:当市场上股票的价格大幅下降到K以下时,它就极大地增加了公司的成本,公司有可能承担不起这种期权,因此公司在采取这种奖励措施时应特别小心,期权合约中确定一个合适的价值保障l是很关键的. 例如,保守的公司可以选择一个比较小的价值保障l.
1 建立模型
这种新型的股票期权作为公司的一种奖励机制,当市场上股票的价格很低时,它为杰出员工提供了一种最低的保障(l-K). 公司确定了一个比敲定价格K稍大的价值保障l,使得股票期权的持有者在实施期权时的收益为(max(l,st)-K),这种新类型的股票期权对员工有更大的吸引力,显然这种新类型期权的价值与价值保障l有关. 下面利用动态规划原理为这种新类型股票期权建立模型,推导出这种新类型股票期权价值所满足的HJB方程.
假设市场不存在套利机会,且无风险利率r>0,风险资产的红利率q≥0,股票的价格st遵循几何布朗运动[9]:
dst=μstdt+σstdWt,
其中Wt为标准布朗运动,μ≥0是期望回报率,σ>0是波动率.
设V(s,l,t)表示此类新类型期权在t时刻的价格,利用动态规划原理,根据It’s公式,可知V(s,l,t)满足以下变分不等式
(1)
(2)
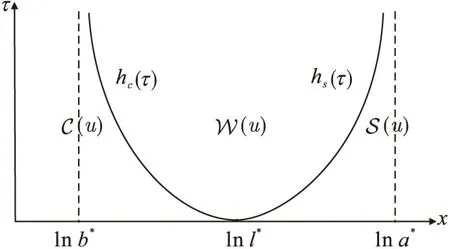
其中QT=×(K,+)×(0,T],xu=∂xxu+(r-q-)∂xu-ru. 由于xu中不含有l的微分,可将l看成参数,则对于任一固定的l (l>K),问题(2)为一个一维抛物障碍问题. 本文第2部分可得到问题(2)的W2,1p,loc(ΩT)解的存在唯一性,其中ΩT=×(0,T].
2 问题(2)的W2,1p,loc解的存在唯一性
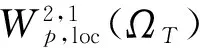
(3)
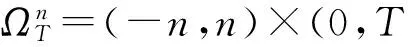
为了证明问题(3)解的存在性,引进惩罚函数βε(t)(图 1)[4],满足
βε(t)C2(-,+),βε(t)≤0,ε(t)≥0,β″ε(t)≤0,
βε(0)=-C0=-[(q+r)en+rl],
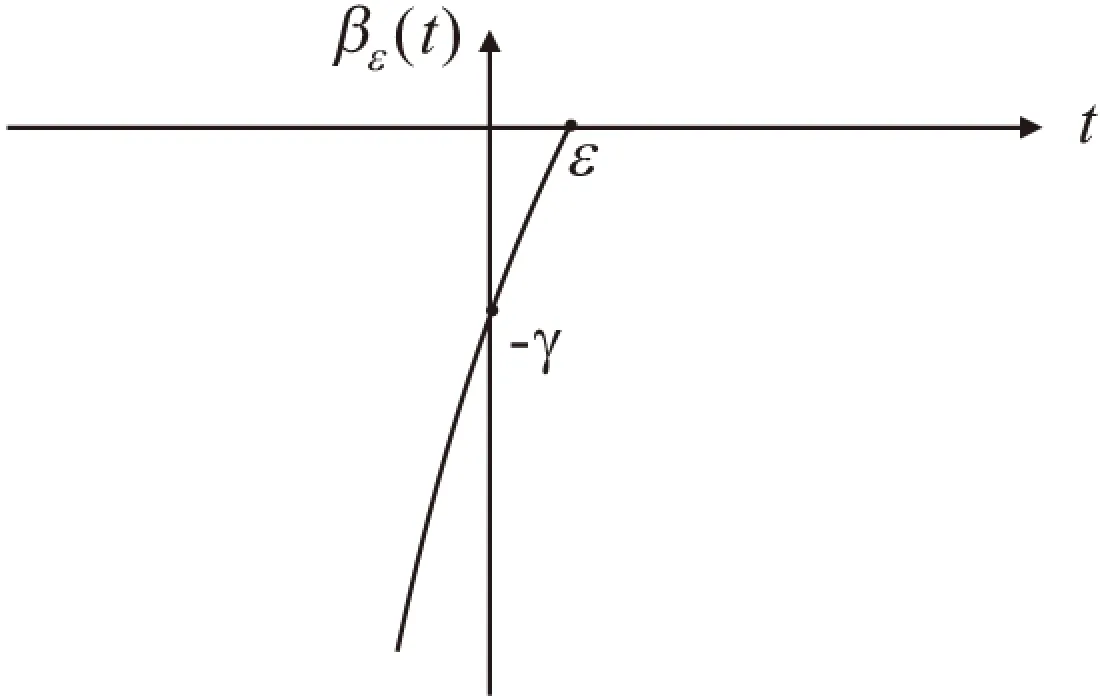
图1 惩罚函数βε(t)
由于(ex-l)+不够光滑, 因此定义逼近函数πε(t)(图 2):
πε(t)C∞,0≤(t)≤1,π″ε(t)≥0,πε(t)=t+.
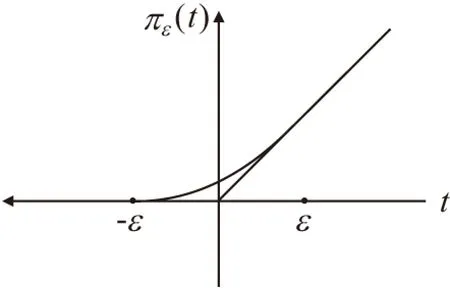
图2 逼近函数πε(t)
现在考虑问题(3)的惩罚问题,对任意固定的ε>0,uε,n(x,l,)满足
(4)
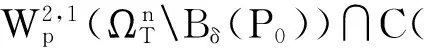
(ex-l)++l-K≤un≤ex+2l-K((x,)ΩnT),
(5)
∂un(x,l,)≥0 ((x,)ΩnT),
(6)
∂xun(x,l,)≥0 ((x,)ΩnT).
(7)
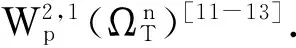
接下来证明当n充分大时,有
πε(ex-l)+l-K≤uε,n≤ex+2l-K ((x,)ΩnT).
(8)
令v1(x)=πε(ex-l)+l-K,注意到当ε充分小,有
πε(ex-l)+l-K≤ex+ε+l-K≤ex+l.
则由C0的定义有
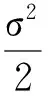
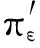
C0≤qex+r(πε(ex-l)+l-K)-C0≤0,
且v1(x)满足初边值条件:
联合式(4),应用比较原理[14-15],有
πε(ex-l)+l-K≤uε,n.
以下证明式(8)的右端. 记v2(x)=ex+2l-K,对任意的0<ε qex+r(2l-K)+βε(ex+2l-K-(πε(ex-l)+l-K))≥ qex+r(2l-K)+βε(ε)≥0. 因此,v2(x)满足 应用比较原理,有uε,n≤ex+2l-K,因此证得式(8). 因为uε,n为式(4)的解且满足式(8),根据文献[16],令ε→0,有 结合问题(3),由变分不等式的解关于初值的单调性,有 最后证明式(7). 在式(4)两边对x求导,记v(x,l,)=∂xuε,n(x,l,),那么v满足 ∂xuε,n(x,l,)=v(x,)≥0, 令ε→0证得式(7). u2(x,l,)>u1(x,l,)≥(ex-l)++l-K, 则对(x,),∂u2-xu2=0,∂u1-xu1≥0. 记ω(x,)=u2(x,l,)-u1(x,l,),则ω(x,)满足 其中∂p是的抛物边界. 由极值原理,得到 定理1 对任一固定的l>K,对任意的R>0,δ>0,0 证明对任一固定的l>K,问题(3)可写成以下形式 (12) 且由Sobolev嵌入定理,有 本节将研究问题(2)的自由边界的性质. 对任意固定的l>K,记 (u)={(x,)|u(x,l,)>++l-K}, (13) (14) 由比较原理知 由式(11)和式(13),可知 ∂x(u-(l-K))≥0,∂x(u-(ex-K))≤0. 因此,定义自由边界为: hc()=max{x|u(x,l,)=l-K} (0<≤T), hs()=min{x|u(x,l,)=ex-K} (0<≤T). 从金融上看,如果股票的价格st非常高,则应立即实施这张股票期权,此时的收益为st-K. 同理,若股票的价格st 下面考虑当q>0时,自由边界hc()和hs()的有界性、 单调性、连续性以及光滑性. 文献[18]考虑了此新类型股票期权在无限时间内的定价问题,指出此新类型的永久美式期权的价值满足下面的稳态问题: (15) 给出了解(V0(s,l),b*,a*),即无限时间内新类型股票期权的价值满足 其中γ0和γ1为r=(r-q)γ+σ2γ(γ-1)/2的解,a*>l,b* (16) (17) 其中c*=a*/b*是 的唯一的大于1的实根 利用相对应稳态问题的自由边界性质及比较原理,可得到自由边界hc()、hs()的有界性. 定理2hc()和hs()(图 3和图 4)满足 lnb*≤hc()≤lnl, (18) (19) 其中a*、b*为式(16)、(17)所给出的表达式. 证明 显然有hc()≤lnl≤hs(). 由于(V0(s,l),b*,a*)是问题(15)的解, 其中b* u0(x,l)≥u(x,l,) ((x,)×[0,T]). 显然 ⊆ ⊆ 即lnb*≤hc(),hs()≤lna*. 当(x,)(u),即u(x,l,)=ex-K时,有 ∂u-xu=qex-rK≥0, 则x≥ln(rK/q),因此,由hs()的定义,证得 hs()≥max{lnl,ln(rK/q)}. 从金融上看,永久美式期权V0(s,l)比一般美式期权V(s,l,t)拥有更多的获利机会,所以V0(s,l)≥V(s,l,t),且由于永久美式期权并无到期日,则期权持有者可以等到期权价值更高时才实施期权,故对永久美式期权而言实施股票期权的范围更小. 接下来考虑自由边界的单调性. 定理3 hc()关于是严格单调递减的函数,hs()关于是严格单调递增的函数. 证明 由式(10)得 (20) 由式(20)和hc()的定义,可知hc()是单调递减的. 事实上,hc()是严格单调减的,如果x=hc()有垂直的部分Γ={(x*,)|1≤≤2},那么在Γ上,u=l-K,∂xu=0,∂u=∂u=0. 又因为 hc()单调递减说明了:随着→0,即离到期日越来越近时,最佳实施边界x=hc()越来越大. 从金融上看,离到期日越来越近时,若此时市场上的股票价格S(t) 由于hc()关于是严格单调递减的,hs()关于是严格单调递增的,则定义 定理4hc()、hs()在(0,T]上连续(图 3和图 4),且 hc(0)=lnl, (21) hs(0)=max{lnl,ln(rK/q)}, (22) 特别地,hc(),hs()C(0,T]. 证明 首先证明式(21). 我们知道hc(0)≤lnl, 如果hc(0) 特别地,∂xu(x,l,0)=0,∂xxu(x,l,0)=0. 在=0上,由方程(3)得 接下来证明hc()在[0,T]上是连续的. 如果hc()在[0,T]上不连续,则存在0>0,使得 由于 同理可证hs()在[0,T]上连续,且hs(0)=max{lnl,ln(rK/q)}. 由∂u(x,l,)≥0及((ex-l)++l-K)为下障碍,可利用文献[11]、[19]、[20],同样的论证证得hc(),hs()C(0,T]. 证毕. 图3 自由边界hc()和hs() (l≥rK/q) 图4 自由边界hc()和hs() (K 从金融上来讲,当利益保障l越大时,期权的收益就越高,则期权越贵,对员工的吸引力也越大. 但是当l越大时,公司发行该期权的成本也就越高,因此选择合适的l对公司来说是很重要的. 接下来将考虑期权价值以及自由边界与利益保障l的关系. 证明 设ui(x,li,)(i=1,2)为以下问题的解: 定理6 hc()与hs()关于l是严格单调递增的. 证明 由定理5可知,当K 下证hs2() 下证hc2() ((x,)ΩT,i=1,2). 则由ui(s,li,)为问题(2)的解,可知)满足 因为 根据变分不等式关于非齐次项、障碍及初值的单调性可知 0≤u1(x,l1,)-(l1-K)≤u2(x,l2,)-(l2-K), 同理,利用Hopf 引理可以证得hc2() 下面讨论q=0时,hc()和hs()的性质. 由比较原理,容易证明以下引理. 引理3 假设u1(x,)为不支付红利的标准美式看涨期权的解,即u1(x,)为下面问题的解: (23) 文献[18]还考虑了当q=0时,新类型永久股票期权的问题,其价值满足下面的稳态问题: 类似于定理2、定理4的证明,可得 定理7 当q=0时,hc()关于为严格单调递减的函数,且满足 lnl*≤hc()=lnl, 特别地,hc()C[0,T]∩C(0,T]. [1]BENSOUSSANA.Onthetheoryofoptionpricing[J].ActaApplicandaeMathematicae,1984,2(2):139-158. [2]BLACKF,SCHOLESM.Thepricingofoptionsandcorporateliabilities[J].JournalofPoliticalEconomy,1973,81(3):637-654. [3]KARATZASI.OnthepricingofAmericanoptions[J].AppliedMathematics&Optimization,1988,17(1):37-60. [4]JIANGL.Mathematicalmodelingandmethodsofoptionpricing[M].Singapore:WorldScientific,2005. [5] 徐振斌. 期权激励与公司长期绩效通论[M]. 北京:中国劳动社会保障出版社,2003. [6]VANMOERBEKEP.Onoptimalstoppingandfreeboundaryproblems[J].ArchiveforRationalMechanicsandAnalysis,1976,60(2):101-148. [7]CHENXS,SONGQS,YIFH,etal.CharacterizationofstochasticcontrolwithoptimalstoppinginaSobolevspace[J].Automatica,2013,49(6):1654-1662. [8]CHENXS,YIFH.FreeboundaryproblemofBarenblattequationinstochasticcontrol[J].DiscreteandContinuousDynamicalSystems:SeriesB,2016,21(5):1421-1434. [9]WILMOTTP,DEWYNNEJ,HOWISONS.Optionpricing[M].Oxford:OxfordFinancialPress,1993. [10]GILBARGD.Ellipticpartialdifferentialequationsofsecondorder[M]. 2nded.Berlin:Springer,1983. [11]FRIEDMANA.Parabolicvariationalinequalitiesinonespacedimensionandsmoothnessofthefreeboundary[J].JournalofFunctionalAnalysis,1975,18(2):151-176. [12]JAILLETP,LAMBERTOND,LAPEYREB.VariationalinequalitiesandthepricingofAmericanoptions[J].ActaApplicandaeMathematicae,1990,21(3):263-289. [13]YANGZ,YIFH.AvariationalinequalityarisingfromAmericaninstallmentcalloptionspricing[J].JournalofMathematicalAnalysis&Applications,2009,357(1):54-68. [14]EVANSLC.Partialdifferentialequations[M]. 2nded.Providence,RI:AmericanMathematicalSociety,2010. [15]TSOK.OnanAleksandrov-Bakel’Mantypemaximumprincipleforsecond-orderparabolicequations[J].CommunicationsinPartialDifferentialEquations,1985,10(5):543-553. [16]SIMONJ.CompactsetsinthespaceLspp(0,T;B)[J].AnnaliDiMatematicaPuraEdApplicata,1987,146:65-96. [17]陈亚浙. 二阶抛物型偏微分方程[M]. 北京:北京大学出版社,2003. [18]GUOX,SHEPPL.Someoptimalstoppingproblemswithnontrivialboundariesforpricineexoticoptions[J].JournalofAppliedProbability,2001,38(3):647-658. [19]CANNONJR,HENRYDB,KOTLOWDB.ContinuousdifferentiabilityofthefreeboundaryforweaksolutionsoftheStefanproblem[J].BulletinoftheAmericanMathematicalSociety,1974,80(1974):45-48. [20]FRIEDMANA.Variationalprincipleandfreeboundaryproblems[M].NewYork:JohnWiley&Sons,1982. 【中文责编:庄晓琼 英文审校:肖菁】 Free Boundary Problem of A New Type of American Option CHEN Xiaoshan1*, CAO Limin2, YI Fahuai1 (1. School of Mathematical Science, South China Normal University, Guangzhou 510631, China; 2. Langfang Yanjing Polytechnic College, Sanhe 065200, China) A parabolic variational inequality with two free boundaries arising from a new type of stock option pricing is considered, which provides a guaranteed minimum as an added incentive in case the market appreciation of the stock is low. The existence and uniqueness of solution to the problem via the PDE technique are proved. Moreover, the existence, monotonicity and smoothness of two free boundaries, and the relationship between the solution to the parabolic variational inequality and the guaranteed minimum are obtained. option pricing; variational inequality; free boundary 2016-12-28 《华南师范大学学报(自然科学版)》网址:http://journal.scnu.edu.cn/n 国家自然科学基金项目(11601163); 广东省自然科学基金项目(2016A030313448) O29 A 1000-5463(2017)04-0095-07 *通讯作者:陈晓珊,讲师,Email:xschen@m.scnu.edu.cn.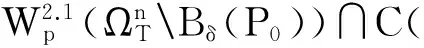
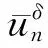

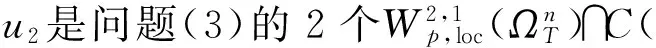
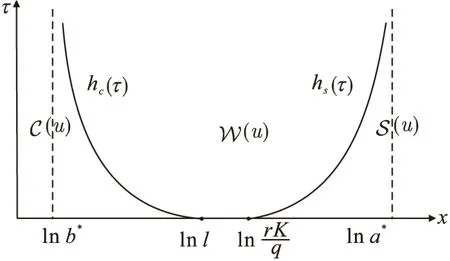
3 自由边界的性质