金属玻璃流变的扩展弹性模型∗

王军强欧阳酥

(中国科学院宁波材料技术与工程研究所,中国科学院磁性材料与器件重点实验室,

浙江省磁性材料及其应用技术重点实验室,宁波 315201)

Wang Jun-Qiang†Ouyang Su

(CAS Key Laboratory of Magnetic Materials and Devices,Key Laboratory of Magnetic Materials and Application Technology of Zhejiang Province,Ningbo Institute of Materials Technology and Engineering,Chinese Academy of Sciences,Ningbo 315201,China)

专辑:非晶物理研究进展

金属玻璃流变的扩展弹性模型∗

王军强†欧阳酥

(中国科学院宁波材料技术与工程研究所,中国科学院磁性材料与器件重点实验室,

浙江省磁性材料及其应用技术重点实验室,宁波 315201)

(2017年4月17日收到;2017年5月2日收到修改稿)

玻璃-液体转变现象,简称玻璃转变,被诺贝尔物理学奖获得者安德森教授评为最深奥与重要的凝聚态物理问题之一.金属玻璃作为典型的非晶态物质,具有与液体相似的无序原子结构,因此又称为冻结了的液态金属,是研究玻璃转变问题的理想模型材料.当加热至玻璃转变温度,或者加载到力学屈服点附近时,金属玻璃将会发生流动.由于热或应力导致的流动现象对金属玻璃的应用具有重要意义.本文简要回顾了金属玻璃流变现象,综述了流变扩展弹性模型的研究进展和未来发展趋势.

金属玻璃,流动,弹性模型

1 引 言

1.1 玻璃转变

液体的流动可能是最广为人知的流动现象.除了液体,有很多物质可以发生流动,比如空气、沙堆、谷堆、交通(汽车和人群)等.这些“物质”有一个共同点:组成单元处于无序排列的状态,均可以认为是非晶态.玻璃-液体转变现象(简称玻璃转变)是冻结的非晶态结构开始流动(或其逆过程)的典型物理模型.玻璃转变是凝聚态物理中尚未清晰理解的重要问题之一[1].随着温度的降低,液体中原子或分子运动变得越来越缓慢,最终在冷速允许的实验观察时间尺度内无法达到平衡态而被“冻结”成玻璃态.伴随着过冷液体的“冻结”过程,其体积或焓随温度的变化率在玻璃转变处会连续降低,这与液体-晶体的凝固过程发生的突变行为完全不同[2].玻璃转变一般伴随着材料物理性能的显著变化,但其原子结构并没有明显的影响.过冷液体的黏度随着温度的降低而逐渐增大,并在接近玻璃转变温度的较窄的温度范围内增加几个数量级[3],如图1所示.这一动力学的巨大变化一直是个谜[2].所以一般认为玻璃转变是一个动力学过程(非晶态结构的冻结和解冻),而非相变过程.

过冷液体的动力学性质(如黏度、扩散系数等)随温度的变化关系可以用Angell图表征[3],如图1所示.当T=Tg时,不同材料的黏度数据会交于一点,1012Pa.s;当温度趋向于无穷大时,也交汇于同一点,10−4Pa.s[3,4]. 通常用Angell图中Tg附近的斜率表征液体动力学行为随温度的依赖性,即脆性(m).其定义如下:η0是黏度的高温极限,一般为10−4Pa.s,ΔE(T)是不同温度下的流动激活能,kB是玻尔兹曼常数.m值越小则液体越强(strong),表现在Angell图中就是越接近Arrhenius关系;m值越大则液体越弱(fragile),表现在Angell图中就是偏离Arrhenius关系越远.对于金属玻璃来说其m值的范围通常在25—65范围内.

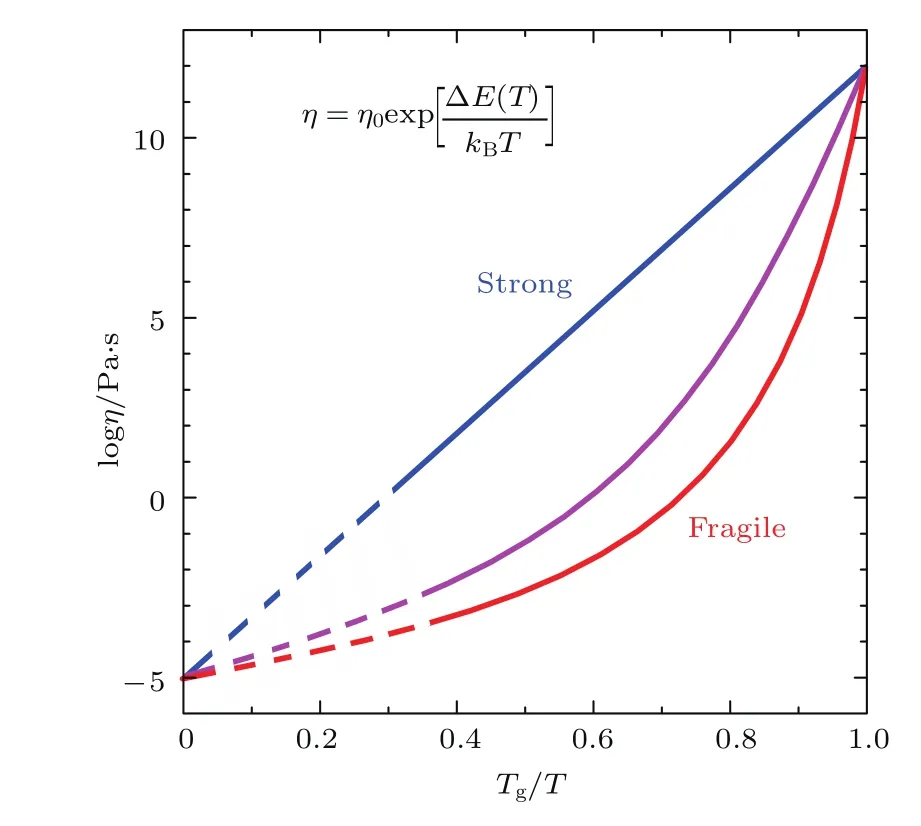
图1 液体黏度与温度的依赖关系Angell示意图 在玻璃转变温度附近和极高温度时,所有液体的黏度都变得相同,当流动激活能ΔE表现为不随温度变化的常数时,为“强”(strong)液体;当ΔE随着温度的升高而减小时,为“脆性”(fragile)液体[3]Fig.1.Angell plot of temperature-dependent viscosity. At glass transition temperatures and in fi nitely high temperature,the viscosity of all liquids are identical.If the energy barrier for fl ow is less temperaturedependent,the liquid is strong;if the energy barrier is temperature-dependent,the liquid is fragile[3].

1.2 应力下的流变

无序的原子结构使得金属玻璃往往表现出极高的屈服强度(接近理论强度)、较大的弹性变形(弹性极限约2%)、良好的耐磨性能及耐腐蚀性能等.很多金属玻璃体系都表现为完全脆性断裂的力学行为[5,6],只有部分金属玻璃在特定条件下表现出一定的压缩塑性[7−10].晶态材料的力学性质主要依赖于它们的晶体结构和电子结构,塑性变形能力与位错和晶界等缺陷的运动密切相关.与晶态材料不同,金属玻璃在室温附近的屈服变形行为往往由只有几个纳米厚度的剪切带承载,剪切带越多的金属玻璃塑性变形能力越强[7,9,11].随着温度和加载速率的变化,金属玻璃的塑性变形行为也会变化.在高温和低应变速率条件下,非晶合金发生均匀变形,此时塑性变形均匀分布在每个体积单元中;而在低温和高应变速率条件下,非晶合金发生非均匀变形,塑性变形被高度局限于剪切带中,造成剪切带材料的黏度下降,导致局部软化和脆性断裂[12−14],从而严重限制了块体非晶合金在结构材料领域内的应用.实验观测到剪切带内部原子以及断面上已经发生了流动现象[15,16](图2).而通过热力学计算,金属玻璃断裂所需机械能量与玻璃转变所需热量一致[17],这与自由体积模型的预测一致[18].同时,理论计算发现温度和应力对液体黏度的作用是等效的[19].因此,金属玻璃在应力下流变行为与热致玻璃转变现象在能量机理上是一致的.那么金属玻璃流动的激活能由什么决定呢？

图2 金属玻璃断面液滴状和丝状液体痕迹[15]Fig.2.The fl ow characters on the fracture surface of metallic glasses[15].

2 金属玻璃流变的弹性模型

针对金属玻璃的流变现象,人们提出了一些微观模型[20−24]:比如变形导致的膨胀或自由体积模型[24]、原子团协作剪切行为或称为剪切形变区模型(STZ)[22,23,25,26]、流动单元模型[20,27−29]、核壳模型[21,30,31]等.简言之,自由体积就是一个原子最近邻位置存在的空隙,它可以毫不费力地进入的区域.对于金属玻璃来说,其内部的自由体积在统计意义上是均匀分布于体系所有原子周围的.为了使金属玻璃发生流动,必须使其内部的自由体积含量增加.数值计算的结果显示,当约化自由体积含量达到2.4%时,流动将会发生[32].与颗粒阻塞(jamming)系统[33]一样,增加金属玻璃中的自由体积有多种方法,比如施加应力、升温等.自由体积模型对我们直观地理解流动现象非常有帮助.但是很难定量测量其变化,这也直接限制了自由体积模型的广泛应用.剪切形变区模型认为承担塑性流动的基本单元中包含几十至上百个原子[23].在承受应力时,这些原子会以一种协作的方式共同流动克服周围基体的弹性束缚耗散能量[25,34,35].一般自由体积含量多的地方更容易发生剪切流变形成剪切流动区.流变单元模型认为金属玻璃内部原子堆积具有不均匀性,自由体积富集的地方在温度和应力的激发下将首先发生流动[20],这些流变单元也是各种非均匀弛豫行为的结构起源.核壳模型主要是针对非晶合金的应力响应行为提出的,认为这些容易发生流动的区域被堆积更致密的原子壳层包围,形成一个微型的黏性-弹性系统[20,21,30,31].

虽然这些金属玻璃流变理论模型名称和表述方式有所差异,但描述的微观图像相似.原子堆积疏松、相互作用弱的地方更容易发生流动,但是其流动同时受到周围原子的束缚.如图3所示,在温度和应力作用下,流变单元可以突破弹性壳层的束缚,从而发生宏观流动.因此流动势垒(或者称为激活能)与弹性外壳的强度密切相关.流动的弹性模型认为流动势垒与材料的弹性参数成正比.弹性模型因为将弹性模量和流动激活能联系起来使得测量及定量表征更加准确.“挤推模型”[36,37]作为弹性模型的代表,认为流动激活能可以表示为剪切模量(G)和特征体积(Vc)的乘积形式,ΔE=GVc.然而特征体积Vc的具体物理含义以及如何测量仍然不清楚.Johnson和Samwer[25]提出的剪切协作模型中的流变势垒可以表示为ΔE=(8/π2)γ2cζGΩ,其中,G是剪切模量,Ω是流变单元体积,γc是屈服应变(约为0.02),ζ是矫正常数(约为3).Spaepen[38]认为剪切流动过程中的能量势垒可以表示成ΔE=τΩ∗,其中τ=Gγ是剪切应力,Ω∗是原子体积.Argon[23]的自由体积模型提出在剪切流变的过程中,可能伴随着剪胀作用,其流变势垒可以表示为ΔE=[(7−5v)/30/(1−v)]Gγ20Ωf,其中v是泊松比,Ωf是流变区域的体积.

图3 流变单元在温度或应力作用下开始流动的原子团模型[20]Fig.3.Schematic atomic packing structure for the percolation of fl ow unit under stress or at elevated temperatures[20].

金属玻璃流变弹性模型的发展对准确理解玻璃转变现象、玻璃形成能力、塑性变形和弛豫等物理现象具有重要意义[39].金属玻璃弹性模量与主组元元素模量相近[40,41],同时又符合混合原则[42],即M=∑fiMi,其中M是金属玻璃的弹性模量,Mi是组元元素的弹性模量,fi是该组元所占比例.根据该弹性模量判据,人们设计制备出很多具有特殊性能的块体金属玻璃体系[7,43−46].

综上所述,各种弹性模型都指出金属玻璃的流变势垒与弹性模量和流变特征体积成正比,其中:1)弹性模量主要是剪切模量(G),同时由于剪胀效应,体弹模量(K)可能也有贡献,金属玻璃流变过程中的剪胀效应是国际研究热点问题[39,47−57],虽然剪胀效应的存在已经获得广泛认可,但是剪切和膨胀效应所占比例,即G和K两个模量在流变势垒中的贡献仍然不清楚;2)流变势垒表达式中的特征体积参数的含义仍然不确定,从单个原子体积到流变单元体积(约合几十至几百个原子体积)都有不同的说法.

明确以上两个问题,可以准确理解金属玻璃的玻璃转变现象以及应力下的流变行为,为调控其力学性能提供理论指导.

3 扩展弹性模型

根据Angell等[3]的黏度图可知,在玻璃转变温度和极高温度处,所有液体黏度大小一样.在玻璃转变温度下,这意味着ΔE/(kBTg)是一个常数,因此可以用玻璃转变温度的大小表征玻璃流动的激活能大小.弹性模型意味着流动激活能与弹性模量成正比,即Tg与弹性模量成正比,汪卫华[42,58]通过统计大量实验数据,首次在实验上验证了这个关系.如图4所示,玻璃转变温度与杨氏模量和剪切模量具有正相关性,这是金属玻璃流变符合弹性模型的直接实验证据.然而,图4中的实验数据表明弹性模量与Tg的线性拟合不经过坐标系原点,而且数据点比较离散,两个拟合的统计线性回归参数只有0.755和0.741.RTg是能量的量纲,与弹性模量之间相差一个体积相关的量纲.根据弹性模型理论,二者之间的比值与流动的特征体积相关.

对比热的研究发现,所有的金属玻璃体系玻璃转变前后的比热变化约为3R/2[59].根据德拜比热模型,这意味着在金属玻璃发生流动的过程中每个原子增加了3个自由度.因此,流动激活能中的特征体积可能与材料的各组分元素的平均体积相关.我们统计了46种不同金属玻璃体系的数据.这些体系包括大多数常见的成分,比如Zr—,Cu—,Ca—,Mg—,Ni—,Fe—和稀土基的金属玻璃体系.这些体系的热力学参数分布范围较大,Tg从317 K到930 K,E从23 GPa到195 GPa,泊松比从0.276到0.41[56,57,60].如图5所示,RTg/G(和RTg/E)与平均原子摩尔体积Vm有着非常好的线性关系,线性拟合结果分别为RTg/G=(15.35±0.16)Vm和RTg/E=(5.74±0.05)Vm,而且两个线性拟合的统计线性回归参数也高达0.994和0.996.这说明Vm可以很好地表示金属玻璃流动激活能中的特征体积.

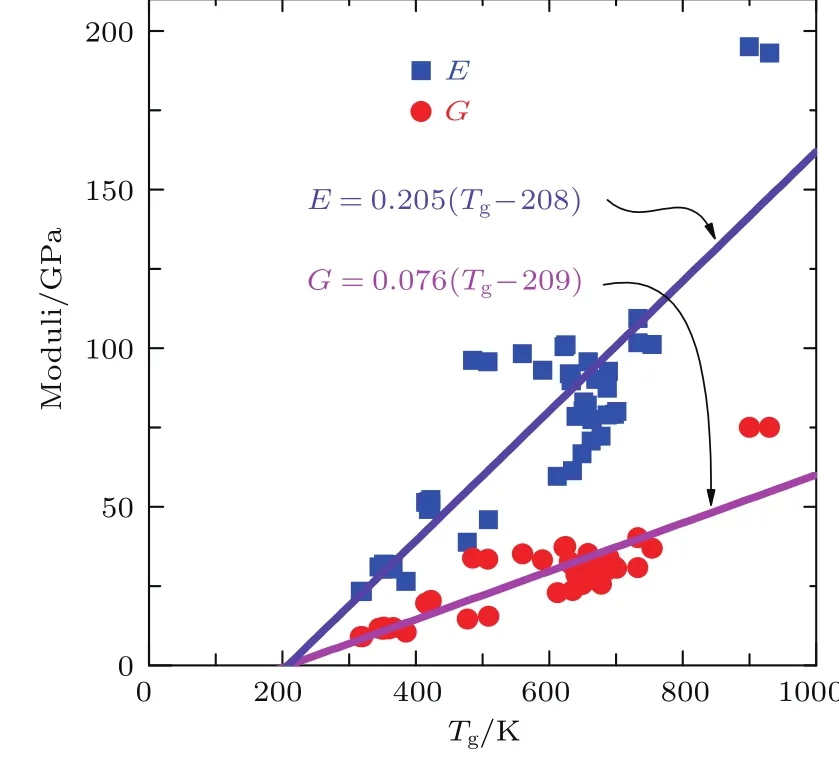
图4 46种不同金属玻璃体系的弹性模量和玻璃转变温度之间的关系 (蓝色方形图标代表杨氏模量(E),红色圆形图标代表剪切模量(G))Fig.4.The relationship between the elastic moduli(Young’s modulus E,shear modulus G)and glass transition temperature.

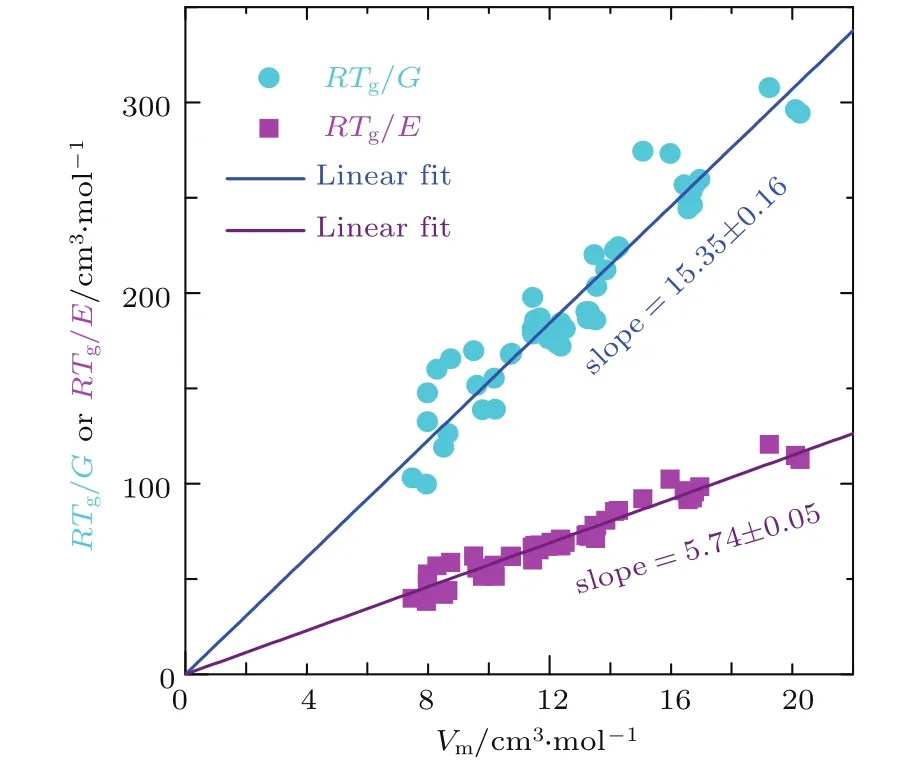
图5 弹性模型中流变特征体积与平均摩尔体积的关系[61]Fig.5.The relationship between the characteristic volume in elastic model and molar volume of metallic glasses[61].

根据上面的结论,容易看出与弹性模量直接相关的不是激活能本身,而是RTg/Vm或ΔE/Vm.定义流动激活能密度ρE[57],

流动激活能密度表示单位体积的原子发生塑性流动所需要的激活能,这样就不用考虑均匀流动和非均匀流动单元激活能中所涉及的特征体积因素.

虽然一般认为流动和金属玻璃的断裂行为都属于剪切运动[23,25,38],但实验研究发现金属玻璃的断裂行为不只是剪切的贡献[62,63],自由体积模型也认为玻璃的流动中有体胀效应,同属于密堆结构的颗粒物质流动发生时也存在明显的剪胀效应[12].根据以上这些现象,有理由推测金属玻璃的断裂和流动行为中既有剪切运动(对应于体积不变的运动行为),也有膨胀效应(体积会变化),即剪胀效应.于是,激活能密度可以表示为剪切模量(G)和体弹模量(K)叠加的形式[57],

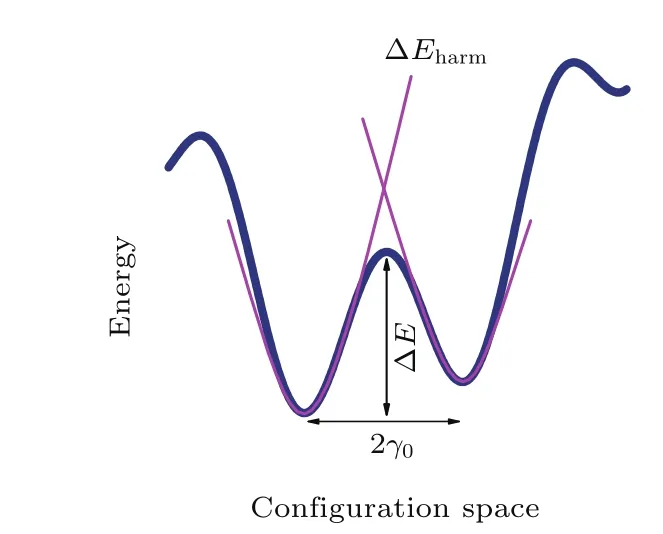
图6 金属玻璃中的能量地图示意图(深色粗线) 两个相邻势阱的距离为2γ0;粉色细线为能量极小值处的泰勒二级近似结果,表示弹性能的简谐近似Fig.6.The schematic energy landscape for metallic glass(thick curve).The distance between two energy minima is 2γ0.The pink thin curves illustrate the harmonic estimation for the energy barrier.

对于图6所示的能量密度地形图(energy density landscape)结构,极小值处可以通过Taylor展开表示为二次抛物线形式[64].弹性能密度可以表示为ρE=Mγ2,这里的M表示弹性模量,γ为弹性应变.这就是能量密度的简谐近似.根据统计热力学中的能量均分定理[65]可以得知M〈γ2〉∝kBT,即〈γ2〉∝ kBT/M. 从图6可以明显看出,根据简谐近似估计的势垒大小(两个抛物线交点)与实际势垒大小成正比,都与能量极小处的曲率(M)成正比.虽然两个抛物线的交点比实际势垒大很多,但是二者的变化趋势一致,于是可以用抛物线交点处能量代表实际势垒,势垒大小可以估计为ρE=. 因为γ0为常数,所以ρE∝ kBT/〈γ2〉.对于金属玻璃来说,升温玻璃转变时每个原子都增加了3个自由度[59].在三维空间中,如果体系增加三个自由度,那么,x,y,z代表直角坐标系中的三个坐标轴方向.对于金属玻璃这种各向同性的物质,M所代表的三个方向的弹性模量包含2个剪切模量和1个纵向模量,即,Mx=My=ρV2S,Mz= ρV2L.于是

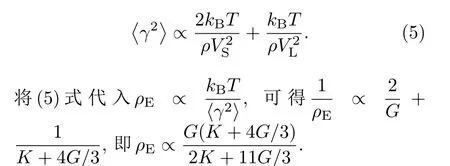
为了准确估算G和K在激活能中所占的比例,将其表示为线性叠加的形式,可以通过研究激活能随温度变化的规律得到,可以由对数微分形式表示[64]:

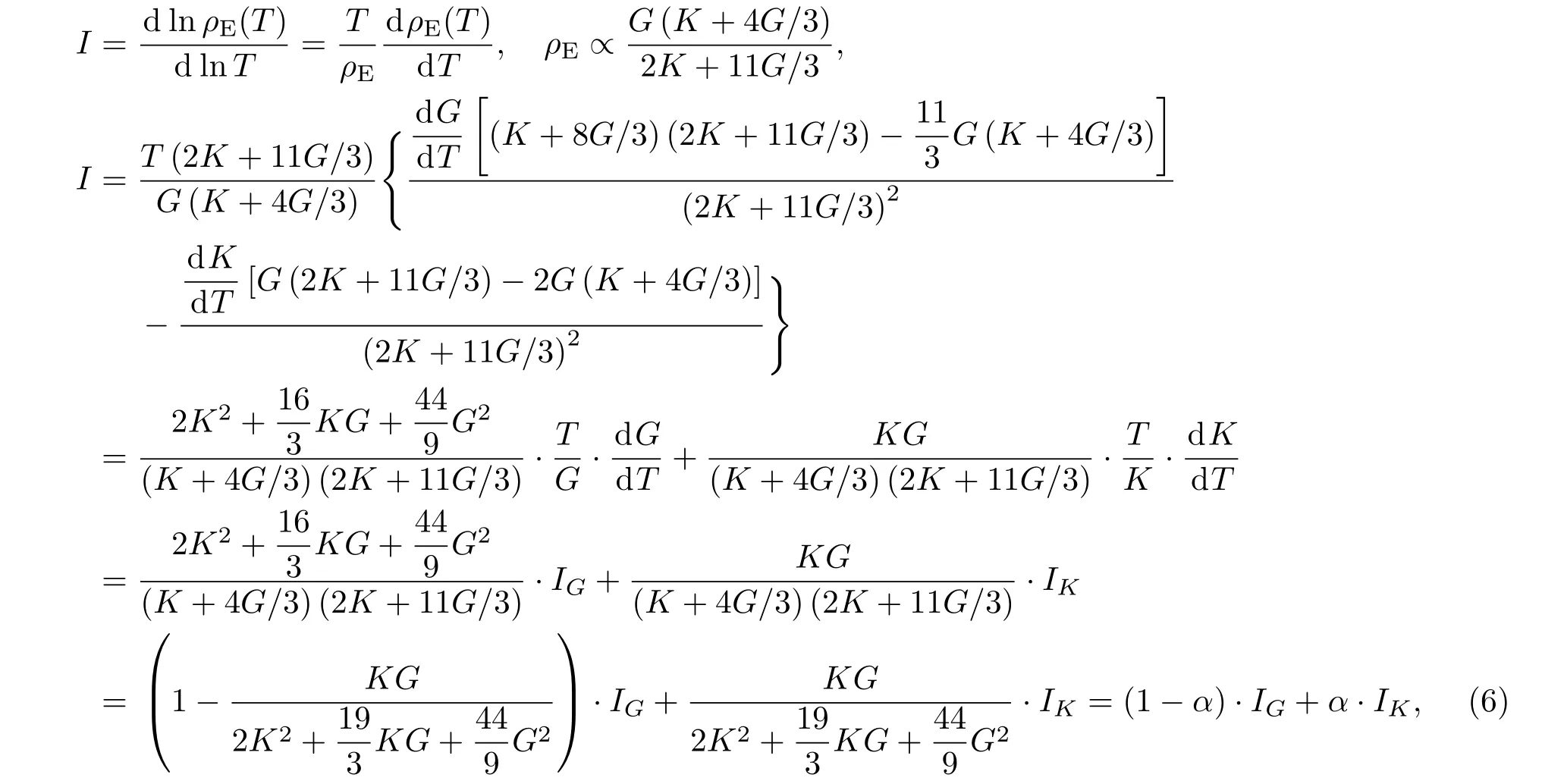
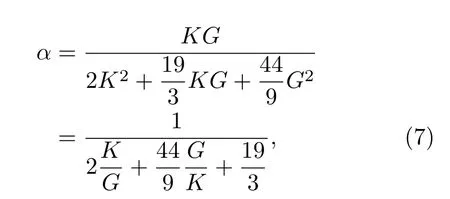
这里的α与(4)式中的含义一致,表示体弹模量随温度的变化对激活能密度随温度变化量的贡献比例,同时也也表示体弹模量对激活能密度的贡献.块体金属玻璃的G/K分布范围为0.2—0.5之间,代入(7)式可得α的分布范围为α=0.071±0.010.这表明体弹模量在金属玻璃激活能中的贡献约为7.1%.

通过测量玻璃转变时弹性模量G和K的变化情况可以验证K在激活能中的贡献比率α.弹性模量可以由声速表示为G=根据这两个表达式,可以得到G和K在玻璃转变处的相对变化量:

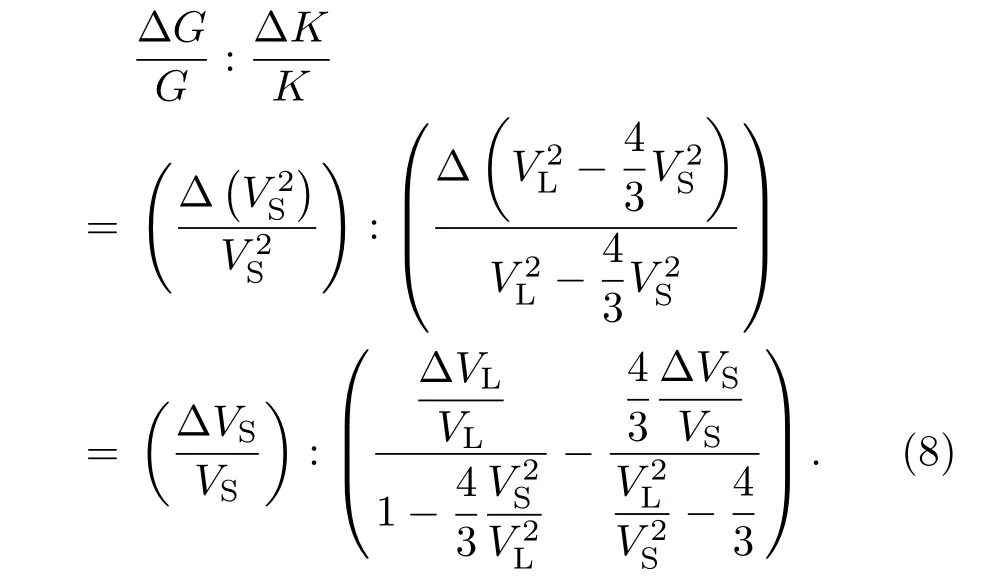
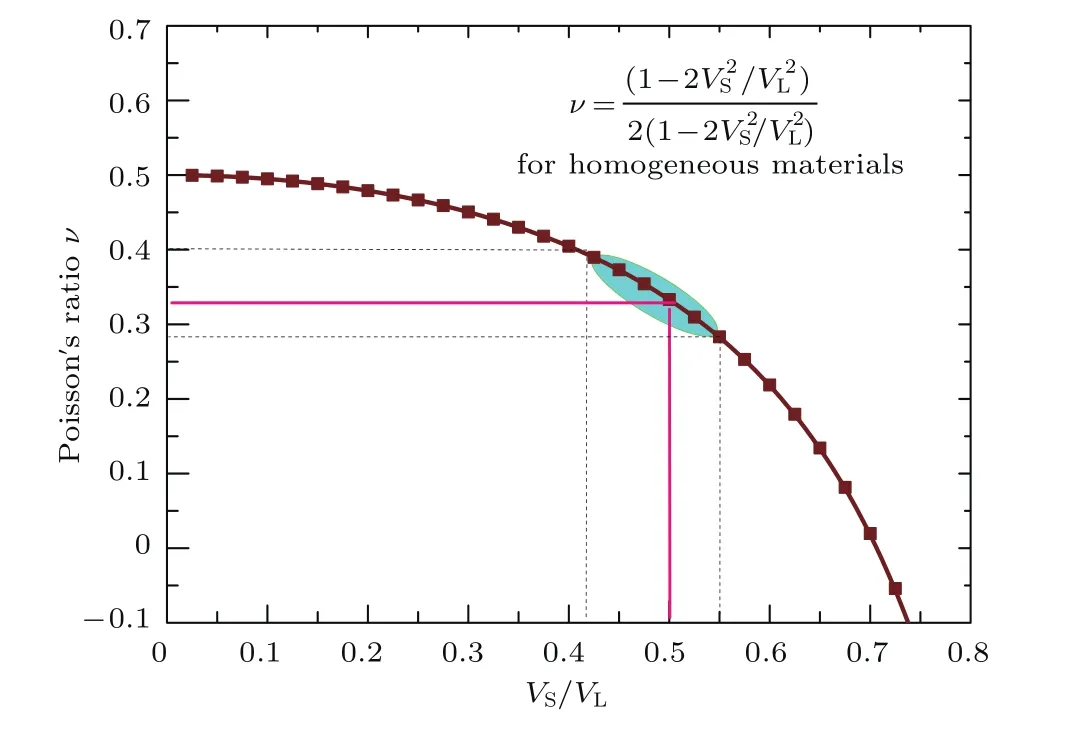
图7 各向同性物质的泊松比和声速的关系(绿色阴影部分为金属玻璃的数据分布范围)[61]Fig.7.The relationship between Poisson’s ratio andsoundvelocity ratio VS/VLfor isotropic materials.The green-shadedzone illustrate the range of metallic glasses[61].

图8 为两种不同玻璃(NaPO3-Al(PO3)3氧化物玻璃[66]和Ce基块体金属玻璃[67])的声速在玻璃转变处的变化情况.可以发现这两种玻璃在玻璃转变处的声速相对变化量大约为2:1.代入(9)式中,得到≈5:1.考虑到在三维空间中,玻璃转变过程中原子释放了三个自由度的运动,这会包含两个剪切模式(对应于G)和一个径向模式(对应于K).剪切模量对金属玻璃流动激活能的贡献应该乘以2.于是,得到G和K在流动激活能中的贡献应该为10:1,即ρE=(10G+K)/11,与前面的结果一致.因此(2)式可以化简为

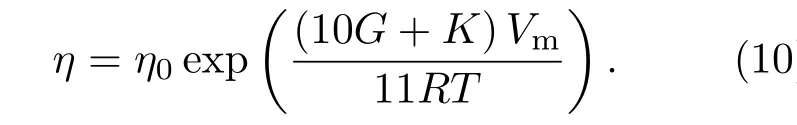
根据弹性模量与Tg的关联性 继续验证上面的结论.根据≡ C(C为常数)和(10)式,应该为常数. 如图9所示,统计了46种不同金属玻璃的数据,发现的值与成分体系没有明显的关系,可以用一个常数0.0753很好地拟合.同时也将的值与46种金属玻璃成分的密度及泊松比的关系绘于图9(b)和图9(c)中,从中都没有发现明显的依赖关系,数据点可以用常数很好地拟合,不依赖于材料体系的性质.再次确认的模型得到的激活能密度ρE=0.91G+0.09K可以描述金属玻璃中原子流动的微观机制.

图8 (a)布里渊区散射法测量的NaPO3-Al(PO3)3氧化物玻璃的纵波(LA)和横波(TA)声速在玻璃转变前后随温度的变化趋势[66];(b)10 MHz超声波方法测量的Ce基块体金属玻璃的纵波和横波声速在玻璃转变前后随温度的变化趋势[67]Fig.8.(a)Thetemperature-dependentlongitudinal and transversalsound velocity ofNaPO3-Al(PO3)3glass measured using Brillouin scattering method[66];(b)the temperature-dependent longitudinal and transversal sound velocity of Ce-based bulk metallic glasses measured using ultrasonic method with a frequency of 10 MHz[67].

单独考虑剪切模量和体弹模型(GVm/Tg和KVm/Tg)都不是常数,而与泊松比ν成线性关系[68],如图10所示.这个结果说明单独G或K都不能很好地表示金属玻璃的流动激活能密度,这与上面讲到的剪胀共存预测一致.

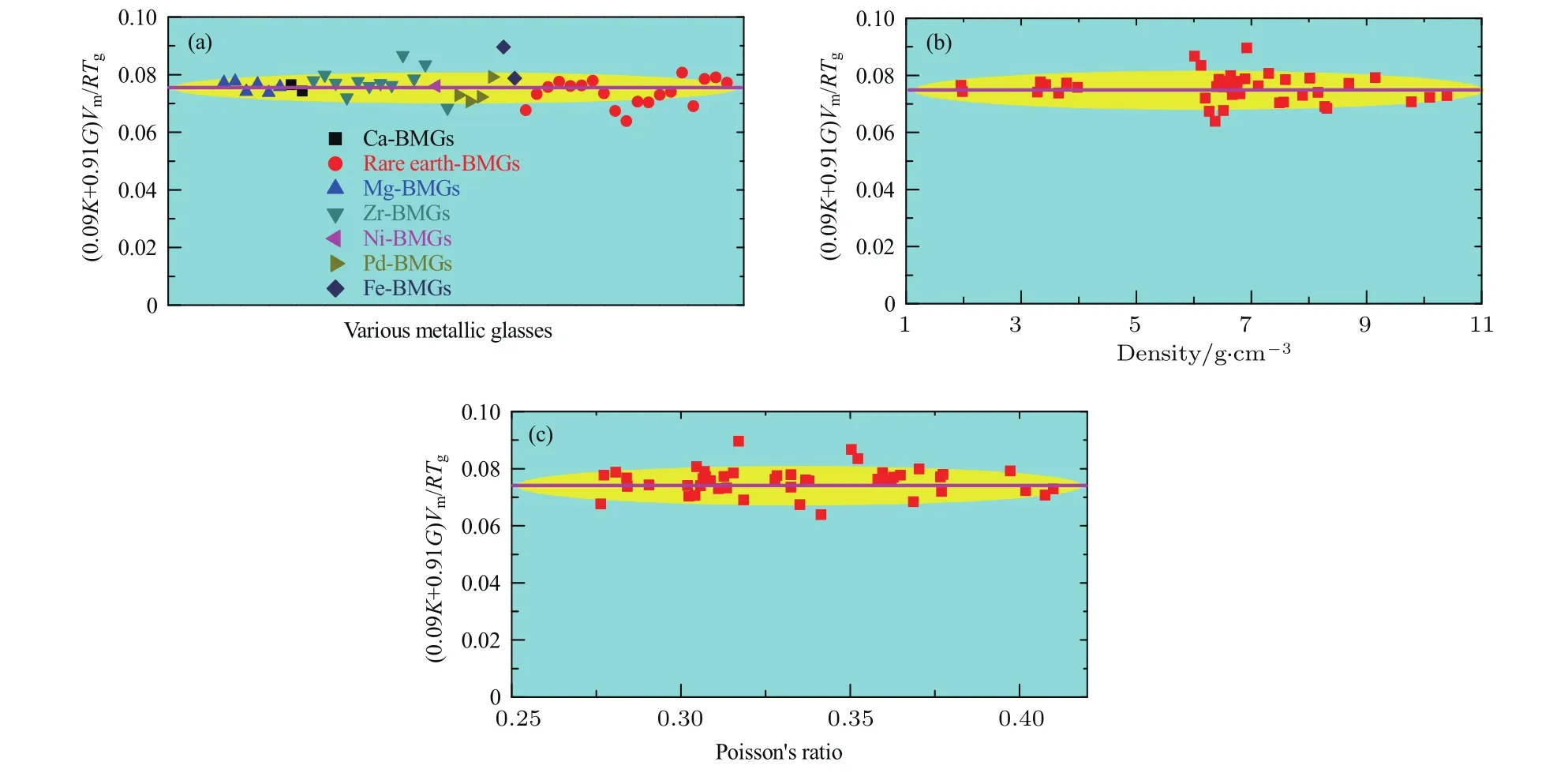
图9 统计发现46种不同块体金属玻璃(BMGs)体系的实验数据(0.91G+0.09K)Vm/(RTg)与材料体系及其性质没有明显的依赖关系,可以用常数0.075拟合得很好[57]Fig.9.The value of(0.91G+0.09K)Vm/(RTg)for 46 kinds of bulk metallic glasses(BMGs)are almost constant which is independent on density and Poisson’s ratio of materials[57].

图10 46种不同块体金属玻璃的(a)KVm/Tg和(b)GVm/Tg与泊松比ν的关系(红色实线为线性拟合结果)[57]Fig.10.(a)KVm/Tg,(b)GVm/Tgversus Poisson’s ratio for 46 kinds of bulk metallic glasses.The pink line is the linear fi tting result[57].

图11 沙子等无序密堆颗粒物质中的剪胀效应Fig.11.The shear-dilatation e ff ect in sands.

4 总结与展望

金属玻璃流变的剪胀效应无疑与其无序原子堆积结构密切相关.颗粒物质(比如沙堆)具有类似的无序密堆结构,金属玻璃中发现的剪胀模型也有望解释颗粒物质的流动剪胀效应.如图11所示,在沙滩上漫步时,沙滩在脚的压力下发生剪切流动的同时,也会发生膨胀,可以有更多的“自由空间”蓄水,因此,脚周围的水会迅速被吸收进去,这就是无序密堆颗粒物质流变过程中的剪胀效应.但剪胀效应与无序密堆结构的确切关系仍然不清楚,颗粒物质流动过程中的剪切和膨胀所占比例亦有待深入研究.

鉴于金属玻璃弛豫行为与弹性模量,以及弛豫与流动现象的密切关系,研究扩展弹性模型与不同弛豫模式的相互影响及其机理,将为调控金属玻璃性质提供理论指导.

扩展弹性模型指出,金属玻璃的流动既有剪切运动也有膨胀效应,剪切和自由体积的产生对玻璃转变或变形引起的流动都是非常重要的,其中膨胀效应对激活能的贡献约占9%.值得注意的是,剪切带形成过程中有外加应力场存在,它包含的膨胀效应或许和无应力态下的玻璃转变现象有一定的区别.

金属玻璃流变属于塑性变形,流变扩展弹性模型提出的流变激活能与弹性模量之间的内禀关系很有趣.弹性模量对金属玻璃室温下的塑性变形能力的影响已经得到广泛研究[69−73].剪切带的形核、扩展和相互作用是决定金属玻璃塑性的三个关键过程和因素,明确金属玻璃流变扩展弹性模型在三个过程中的影响对设计开发具有优异塑性变形能力的金属玻璃具有重要指导意义.

[1]Weintraub H,Ashburner M,Goodfellow P N,Lodish H F,Arntzen C J,Anderson P W,Rice T M,Geballe T H,Means A R,Ranney H M,Cech T R,Colwell R R,Bourne H R,Richter B,Singer I M,Marrack P,Fearon D T,Penzias A,Bard A J,Brinkman W F,Marks P A,Vogelstein B,Kinzler K W,Bishop J M,Zare R N,Schatz G,Benkovic S J,Gray H B,Valentine J S,Crutzen P J,Choi D W,Nakanishi S,Kosslyn S M,Brauman J I,Rees D C,Brill W J,Schell J,Luhrmann R,Will C L,Wulf W,Vermeij G J,Arrow K J,Smelser N J,Anderson D L,Abelson P H 1995 Science 267 1609

[2]Debenedetti P G,Stillinger F H 2001 Nature 410 259

[3]Angell C A,Poole P H,Shao J 1994 Nuovo.Cimento.D 16 993

[4]Mauro J C,Yue Y,Ellison A J,Gupta P K,Allan D C 2009 Proc.Natl.Acad.Sci.106 19780

[5]Wang W H,Dong C,Shek C H 2004 Mater.Sci.Eng.R 44 45

[6]Chen MW 2008 Annu.Rev.Mater.Res.38 445

[7]Liu Y H,Wang G,Wang R J,Zhao D Q,Pan MX,Wang W H 2007 Science 315 1385

[8]Das J,Tang MB,KiMK B,Theissmann R,Baier F,Wang W H,Eckert J 2005 Phys.Rev.Lett.94 205501

[9]Schroers J,Johnson W L 2004 Phys.Rev.Lett.93 255506

[10]Yao K F,Ruan F,Yang Y Q,Chen N 2006 Appl.Phys.Lett.88 122106

[11]Chen MW,Inoue A,Zhang W,Sakurai T 2006 Phys.Rev.Lett.96 245502

[12]Spaepen F 2006 Nature Mater.5 7

[13]Song S X,Nieh T G 2011 Intermetallics 19 1968

[14]Stolpe M,Kruzic J J,Busch R 2014 Acta Mater.64 231

[15]Xia X X,Wang W H,Greer A L 2009 J.Mater.Res.24 2986

[16]Xia X X,Wang W H 2012 Small 8 1197

[17]Liu Y H,Liu C T,Wang W H,Inoue A,Sakurai T,Chen MW 2009 Phys.Rev.Lett.103 065504

[18]Yang B,Liu C T,Nieh T G 2006 Appl.Phys.Lett.88 221911

[19]Guan P F,Chen MW,Egami T 2010 Phys.Rev.Lett.104 205701

[20]Wang W H,Yang Y,Nieh T G,Liu C T 2015 Intermetallics 67 81

[21]Ye J C,Lu J,Liu C T,Wang Q,Yang Y 2010 Nature Mater.9 619

[22]Falk ML,Langer J S 1998 Phys.Rev.E 57 7192

[23]Argon A S 1979 Acta Metall.27 47

[24]Langer J S 2006 Scr.Mater.54 375

[25]Johnson W L,Samwer K 2005 Phys.Rev.Lett.95 195501

[26]Falk ML,Langer J S,Pechenik L 2004 Phys.Rev.E 70 011507

[27]Zhu Z G,Wen P,Wang D P,Xue R J,Zhao D Q,Wang W H 2013 J.Appl.Phys.114 083512

[28]Xue R J,Wang D P,Zhu Z G,Ding D W,Zhang B,Wang W H 2013 J.Appl.Phys.114 123514

[29]Liu S T,Wang Z,Peng H L,Yu H B,Wang W H 2012 Scr.Mater.67 9

[30]Ke H B,Zeng J F,Liu C T,Yang Y 2014 J.Mater.Sci.Tech.30 560

[31]Huo L S,Zeng J F,Wang W H,Liu C T,Yang Y 2013 Acta Mater.61 4329

[32]Wang J G,Zhao D Q,Pan MX,Wang W H,Song S X,Nieh T G 2010 Scr.Mater.62 477

[33]Liu A J,Nagel S R 1998 Nature 396 21

[34]Mayr S G 2006 Phys.Rev.Lett.97 195501

[35]Zink M,Samwer K,Johnson W L,Mayr S G 2006 Phys.Rev.B 73 172203

[36]Dyre J C,Wang W H 2012 J.Chem.Phys.136 224108

[37]Hecksher T,Dyre J C 2015 J.Non-Cryst.Solids 407 14

[38]Spaepen F 1977 Acta Metall.25 407

[39]Wang W H 2012 Prog.Mater.Sci.57 487

[40]Wang W H 2012 Nature Mater.11 275

[41]Ma D,Stoica A D,Wang X L,Lu Z P,Clausen B,Brown D W 2012 Phys.Rev.Lett.108 085501

[42]Wang W H 2005 J.Non-Cryst.Solids 351 1481

[43]Li J F,Wang J Q,Liu X F,Zhao K,Zhang B,Bai H Y,Pan MX,Wang W H 2010 Sci.China:Phys.Mech.53 409

[44]Wang J Q,Wang W H,Bai H Y 2009 Appl.Phys.Lett.94 041910

[45]Zhang B,Zhao D Q,Pan MX,Wang W H,Greer AL 2005 Phys.Rev.Lett.94 205502

[46]Wang Z,Yu H B,Wen P,Bai H Y,Wang W H 2011 J.Phys.Cond.Matter 23 142202

[47]Torre D F H,Dubach A,Loffler J F 2010 J.Alloy.Compd.495 341

[48]Jiang W H,Atzmon M2011 J.Alloy.Compd.509 7395

[49]Liu Z Q,Li R,Wang G,Wu S J,Lu X Y,Zhang T 2011 Acta Mater.59 7416

[50]Yi J,Wang W H,Lewandowski J J 2015 Acta Mater.87 1

[51]Jiang MQ,Jiang S Y,Dai L H 2009 Chin.Phys.Lett.26 016103

[52]Chen Y,Jiang MQ,Dai L H 2011 Sci.China:Phys.Mech.54 1488

[53]Jiang MQ,Wilde G,Dai LH 2015 Mech.Mater.81 72

[54]Jiang MQ,Wilde G,Chen J H,Qu C B,Fu S Y,Jiang F,Dai L H 2014 Acta Mater.77 248

[55]Schmidt V,Rosner H,Peterlechner M,Wilde G 2015 Phys.Rev.Lett.115 035501

[56]Wang J Q,Wang W H,Bai H Y 2011 J.Non-Cryst.Solids 357 223

[57]Wang J Q,Wang W H,Liu Y H,Bai H Y 2011 Phys.Rev.B 83 012201

[58]Wang W H 2006 J.Appl.Phys.99 093506

[59]Ke H B,Wen P,Zhao D Q,Wang W H 2010 Appl.Phys.Lett.96 251902

[60]Wang J Q,Wang W H,Yu H B,Bai H Y 2009 Appl.Phys.Lett.94 121904

[61]Wang J Q 2010 Ph.D.Dissertation(Beijing:Institute of Physics,CAS)(in Chinese)[王军强 2010博士学位论文(北京:中国科学院物理研究所)]

[62]Jiang M,Dai L 2007 Phys.Rev.B 76 054204

[63]Zhang Z F,He G,Eckert J,Schultz L 2003 Phys.Rev.Lett.91 045505

[64]Dyre J C,Olsen N B 2004 Phys.Rev.E 69 042501

[65]Wang Z C 2003 Thermodynamics and Statistics(Beijing:Higher Education Press)pp261–268(in Chinese)[汪志诚2003热力学.统计物理(北京:高等教育出版社)第261—268页]

[66]Dyre J C 2006 Rev.Mod.Phys.78 953

[67]Zhang B,Bai H,Wang R,Wu Y,Wang W 2007 Phys.Rev.B 76 012201

[68]Egami T,Poon S J,Zhang Z,Keppens V 2007 Phys.Rev.B 76 024203

[69]Liu Z Q,Wang W H,Jiang MQ,Zhang Z F 2014 Phil.Mag.Lett.94 658

[70]Liu Z Q,Wang R F,Qu R T,Zhang Z F 2014 J.Appl.Phys.115 203513

[71]Liu Z Q,Zhang Z F 2013 J.Appl.Phys.114 243519

[72]Lewandowski J J,Wang W H,Greer A L 2005 Phil.Mag.Lett.85 77

[73]Gu X J,Poon S J,Shi fl et G J 2011 J.Mater.Res.22 344

Wang Jun-Qiang†Ouyang Su

(CAS Key Laboratory of Magnetic Materials and Devices,Key Laboratory of Magnetic Materials and Application Technology of Zhejiang Province,Ningbo Institute of Materials Technology and Engineering,Chinese Academy of Sciences,Ningbo 315201,China)

PACS:61.43.Dq,81.05.Kf,64.70.peDOI:10.7498/aps.66.176102

*Project supported by the National Natural Science Foundation of China(Grant Nos.11504391,51771216)and the‘100 Talents Project’of Chinese Academy of Sciences.

†Corresponding author.E-mail:jqwang@nimte.ac.cn

Extended elastic model for flow of metallic glasses∗

17 April 2017;revised manuscript

2 May 2017)

Glass-liquid transition phenomenon,usually known as glass transition,has been valuated as one of the most important challenges in condensed matter physics.As typical amorphous solid,metallic glass is composed of disordered-packing atoms,which is akin to a liquid.Thus,metallic glass is also known as frozen liquid.Metallic glass is an ideal model material for studying glass transition phenomenon.When heated up to glass transition temperature or stressed to yielding point,metallic glass fl ows.The fl ow behavior at elevated temperature or under stress plays an important role in the applications of metallic glass.In this paper,we brie fl y review the research developments and perspectives for the fl ow behavior and extended elastic model for fl ow of metallic glasses.

In elastic models for fl ow,i.e.,free volume model,cooperative shear transformation model,it is assumed that the activation energy for fl ow(ΔE)is a combination of shear modulus(G)and a characteristic volume(Vc),ΔE=GVc.Most recently,it has been widely recognized that in amorphous materials,e.g.metallic glass,shear fl ow is always accompanied by dilatation e ff ect.This suggests that besides shear modulus,bulk modulus(K)should also be taken into account for energy barrier.However,what are the contributions of K is still unknown.On the other hand,the physical meaning of characteristic volume Vcand the determination of its value are also important for quantitatively describing the fl ow behavior of metallic glass.Based on the statistical analyses of a large number of experimental data,i.e.,elastic modulus,glass transition temperature,density and molar volume for 46 kinds of metallic glasses,the linear relationship between RTg/G and Vmis observed.This suggests that the molar volume(Vm)is the characteristic volume involved in the fl ow activation energy.

To determine the contribution of K as a result of shear-dilatation e ff ect, fl ow activation energy density is de fi ned as ρE=ΔE/Vm.According to the harmonic analysis of the energy density landscape,we propose that both shear and bulk moduli be involved in fl ow activation energy density,as ρE=(1 − α)G+ αK,with α ≈ 9%.This result is also veri fi ed by the relationship between elastic modulus and glass transition temperature:(0.91G+0.09K)Vm/RTgis a constant,that is,independent of property of metallic glass.This result is also consistent with the evolution of sound velocity with glass transition temperature.

In the end of this review,we address some prospects about the applications of the extended elastic model and its signi fi cance in designing new metallic glasses with advanced properties.This extended elastic model is also fundamentally helpful for understanding the nature of glass transition and kinetic properties of shear band of metallic glasses.

metallic glass, fl ow,elastic model

10.7498/aps.66.176102

∗国家自然科学基金(批准号:11504391,51771216)和中国科学院百人计划资助的课题.

†通信作者.E-mail:jqwang@nimte.ac.cn

©2017中国物理学会Chinese Physical Society

http://wulixb.iphy.ac.cn