在问题引领中实现智慧生长

王卫东

【摘 要】理性与创造是学生必须具备的数学学科素养。培养理性精神、创造能力的过程就是学生智慧生长的过程，而这离不开一个重要的载体——数学问题。基于这样的认识，教者以“认识小数”教学为例，将问题化为智慧生长的“触发器”“助推器”与“引爆器”，从而在问题引领中实现智慧的萌发、丰盈与超越。

【关键词】问题；引领；智慧；生长

中图分类号：G622.0 文献标识码：A 文章编号：1671-0568（2017）22-0018-03

《中国学生发展核心素养（征求意见稿）》指出，学生的核心素养综合表现为社会责任、国家认同、国际理解等9个方面，其涵盖了个人修养、文明修养以及生存与实践方面的素养，核心素养的提出实现了从“教”向“育”的重大转变。就数学学科而言，理性精神与创造能力是学生必须具备的核心素养，这既是对数学知识本质的追寻，也是对数学教学规律的遵从，更是对学生个体发展的尊重。回顾数学发展的历史，从结绳记数到算筹计算，从《九章算术》到《几何原本》……无不充满理性与创造。而学生学习数学的过程也是如此，面对新知，他们需在理性中思辨，在思辨中创造。著名特级教师、“智慧数学”倡导者陈士文认为，理性与创造是数学教育教学中所特有的智慧，培养学生数学学科核心素养的过程就是学生智慧生长的过程。

然而，如何让智慧得以生长呢？换句话说，理性从何而来，创造又如何被实现呢？这一切都离不开一个重要的载体——数学问题。“问题是数学的心脏”，有了问题，才能逼近知识本质；有了问题，才能提升思维品质；有了问题，才能促进智慧生长。为此，在教学“认识小数”时，笔者将数学问题化为智慧生长的“触发器”“助推器”与“引爆器”，在问題的引领中实现了智慧的萌发、丰盈与超越。

一、问题——智慧生长的“触发器”

是什么？为什么？怎么做？有什么用？面对未知世界，人们常常会有这样的困惑，而当学生面对新知时也会产生这样的疑惑。这不是学习能力的倒退、学习品质的下降，而是对未知世界的积极思考，是对未知领域的理性探索。

教材在编排“认识小数”（“苏教版”小学数学三年级下册）教学内容时，安排了这样的两个例题：例1借助分米与米的关系，由整数到分数、进而引入纯小数；例2则是从学习用品的价钱入手，引入带小数。小数在学习生活中有着广泛的运用，学生对此并不陌生，教材从生活情境中引入小数、认识小数也未尝不可。然而，知识是有生命的，它有着自身的生长过程。面对小数，我们不禁要问：在数学发展的长河中，为什么会出现小数？它从哪里来？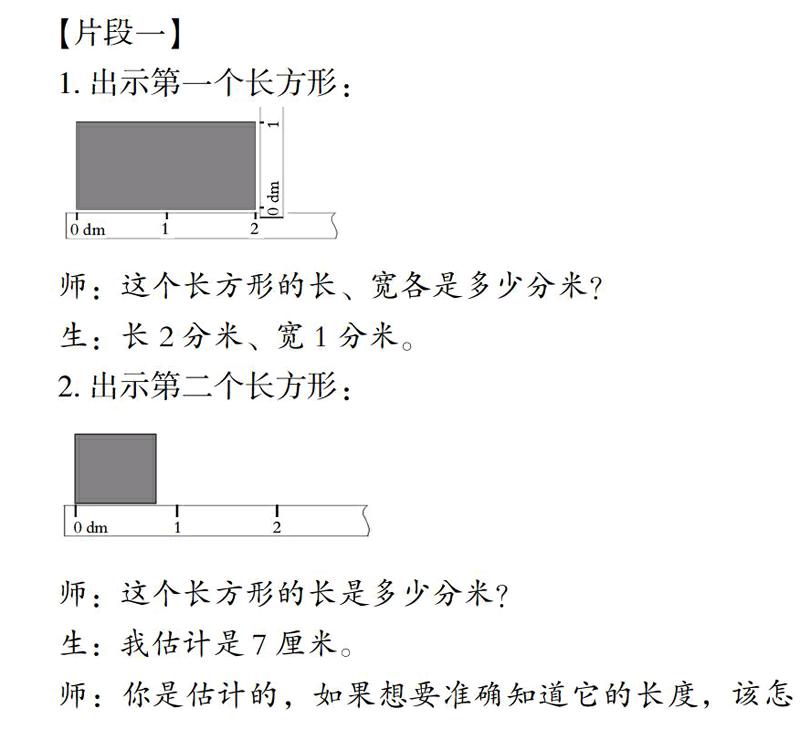

【片段一】

1. 出示第一个长方形：

师：这个长方形的长、宽各是多少分米？

生：长2分米、宽1分米。

2. 出示第二个长方形：

师：这个长方形的长是多少分米？

生：我估计是7厘米。

师：你是估计的，如果想要准确知道它的长度，该怎么办呢？

生：把它分一分。

师：怎么分？能说具体些吗？

生：把1分米平均分成10份，1份就是1厘米。

师：为什么要平均分成10份？

生：1分米里有10厘米。

（课件动画演示平均分的过程）

师：分一分，分米就转化成厘米，现在你能准确地说出它的长度吗？

生：8厘米。

生：■分米。

……

3. 师：同样是长方形，同样用分米做单位，为什么第一个长方形的长和宽能用整数表示，而第二个长方形的长却要用分数来表示呢？

生：因为第二个长方形的长度不足1分米。

师：是的，当整数不好用的时候，我们想到了分一分。在平均分的过程中，我们的祖先创造了分数，还创造了小数。今天我们就一起来认识小数。（板书课题：认识小数）

小数从何而来？小数从“分”中来，在实际生活中，当遇到整数不好用时，小数就出现了，它是人类智慧的创造，也是学生智慧生长的“触发器”。为此，教者以“为什么会产生小数”这个问题为核心，引导学生追溯小数发展的历史，在实际测量的过程中，他们感受到整数表达的局限性，感悟了小数产生的必然性。虽然小数的创造是人类已有的文明成果，但对于学生来说，依然是“第一次”， 他们在“分”的过程中实现了创造，在创造中点燃了智慧的火花。

二、问题——智慧生长的“助推器”

一节课的时间里，教师提出的问题有几十个甚至上百个，然而并非所有的问题都有价值。一般记忆层面的问题、琐碎浅显的问题、机械运用的问题都不是有价值的问题。著名特级教师黄爱华认为，我们要有“大问题研究”的视角，这里的“大问题”就是指有研究价值的好问题，它能激发学习兴趣，促进深度思考，好的问题应成为学生智慧生长的“助推器”。

【片段二】

1. 师：0.4分米，咱们会读了，也会写了，那你会画吗？老师这里为大家准备了3根直条，它们的长度都是1分米，现在你能选择其中的一根，用阴影表示出0.4分米吗？

（学生思考后，完成练习）

师：你为什么会选择第3根直条，而不选择前两个呢？

生：第一个直条没有平均分，而第二个直条虽然平均分了，但没有平均分成10份。

师：哦，是这样啊！那么你认为用小数表示时，应该注意些什么？

生：一定要平均分。

生：而且还要平均分成10份。

师：对，小数是建立在平均分的基础上的，而且今天咱们所学的小数都与平均分成10份有关。

2. 师：下面的图形都表示“1”，请用小数表示出其中的一部分。endprint

（学生发表自己的观点）

师：这里的3幅图都不一样，为什么它们都用0.2来表示呢？

生：它们都被平均分成了10份，取了其中的2份。

师：是的，第1幅图是把一个圆看作“1”，第2幅图是把一个长方形看作“1”，第3幅图是把一条线段看作“1”，它们都被平均分成10份。想一想，“1”还会是什么样子的？

生：三角形。

生：圆形。

……

师：其实不管“1”是什么样子的，只要把它平均分成了10份，其中的2份都可以用0.2来表示。

3. 师：下面的正方形也表示“1”，你能用小数表示出涂色部分吗？

生：涂色部分是0.1。

生：不对，我认为是0.5。

（学生争论起来）

师：刚才的3幅图，大家都一致认为是0.2，为什么对于这幅图，你们却有这么多不同的意见呢？

（学生静场）

生：前面的3个图形都被平均分成10份，而这幅图是平均分成了2份。

师：哦，是这样啊！那你认为涂色部分是多少？

生：0.5。

师：你打算怎样说服大家呢？

生：把第4幅图也来分一分，平均分成10份，这样涂色部分就是5份，也就是0.5了。

师：是这样吗？

课件出示：

什么是小数？对于小数的概念，教材中没有给予严格的数学层面上的定义，其实这也无须学生掌握，但教者却循着理性的眼光，从小数的本质出发，借助三个不同层次的问题教学，从而实現了智慧的生长——首先，通过选择合适的直条来表示0.4分米，让学生在比较分析中明晰“平均分成10份”的重要性，为一位小数模型的建构奠定基础；其次，借助“这里的3幅图都不一样，为什么它们都用0.2来表示呢？”以及“想一想，‘1还会是什么样子的？”的追问，引领学生总结归纳出0.2的意义，即“不管什么样子的‘1，只要把它平均分成了10份，其中的2份都可以用0.2来表示。”从而完成小数意义模型的建构；最后，在“涂色部分是用0.1表示，还是0.5表示”的辩论中，对小数模型进行内化与应用，从而让学生的智慧在问题解决的过程中得以发展和丰盈。

三、问题——智慧生长的“引爆器”

在数学发展的进程中，曾经有过三次数学危机，每一次数学危机的产生都与新问题的提出有关，然而这三次数学危机中没有一次与中国有关，其原因在于中国古代的数学过于倾向“实用主义”，缺少对问题的深度思考与理性探索。在小学的数学课堂上，我们不敢奢望爆发第四次数学危机，但我们却希望让问题成为智慧生长的“引爆器”，以此来激发学生思辨的意识，帮助他们在思辨的过程中造就理性品质、提升创造能力。

【片段三】

课件出示数轴：

……

师：刚才我们在数轴上看到了自然数、分数，下面我们来玩个猜数游戏。老师在这个数轴上也找到了一个数，它在3和4之间，猜一猜，这个数可能是几？

生：3.4。

师：不是，它比3.4大。

生：3.9。

师：也不是，比3.9小。

生：3.6。

师：祝贺你，猜对了。你能在这条线上准确地表示3.6的位置吗？

生：把3和4之间的部分平均分成10份，表示其中的6份。

（课件动画演示平均分的过程，并在数轴上标出3.6）

师：老师还想到了一个数，它也在3和4之间，而且在3.6的附近，你能猜出来吗？

生：3.7。

师：恭喜你，答对了。

（课件出示：在数轴上标出3.7）

师：瞧，这里还有一个数（课件出示：在3.6和3.7之间标出一个点），现在你能知道它是几吗？

生：……

师：这里的数能用3.6表示吗，能用3.7表示吗？（不能）这个数到底是多少呢？你有办法准确地表示出它的位置呢？

生：把3.6和3.7之间的部分再平均分成10份。

师：好，听你的。

（课件动画演示平均分的过程）

师：现在可以准确表示了吗？

生：可以了。

生：老师，我知道！这个数是3.62。

师：你知道的还真不少啊！对于这样的小数，我们以后还会进一步地去学习。大家看，把3和4之间的部分平均分成10份，我们找到了3.6和3.7，把3.6和3.7之间的部分再平均分成10份，我们又得到了新的小数，像这样继续分下去，得到的数就会越来越多，越来越密了！

知道了“小数是什么”“小数从哪里来”，那么接下来“小数要走向哪里”呢？学生的思考还应继续，智慧还应生长。在前面的教学中，教者在教材（第88页“想想做做”第4题）的基础上，围绕数轴进行了资源的挖掘与整合，从不同维度为学生展现了数的魅力：从自然数到分数、小数；从基数的认知到序数的表达；从数的大小比较到数的位置排列；从一位小数到两位小数，甚至多位小数；从数的有限到数的无限……教者为学生打开了一扇天窗，他们感悟到了数的体系的整体性、系统性，从而实现了智慧的超越。

“数学是美的，其中蕴藏一种至简至和的智慧；数学是理性的，其中蕴藏一种至真至通的智慧；数学是自由的，其中蕴藏一种创造探索的智慧。”数学中所蕴藏的智慧从问题中来，又到问题中去。就在提出问题、解决问题、再提出问题，再解决问题的反复过程中，学生的智慧得以萌发、生长与超越，他们在化转与通达间感悟到了理性的智慧，在探究与实践间享受到了创造的乐趣。

（编辑：胡 璐）endprint