载荷识别技术在振动分析中的应用
陈功 曾宪钰 金路 言思敏 / 上海市质量监督检验技术研究院
载荷识别技术在振动分析中的应用
陈功 曾宪钰 金路 言思敏 / 上海市质量监督检验技术研究院
以管换热管为研究对象,介绍了基于Newmark-β法的载荷识别的正反分析原理。通过在MATLAB中编写相应程序,对单根换热管的振动进行载荷识别并计算,分析了传感器布置位置的不同对载荷识别测量结果的影响,从而给今后换热管振动的防振设计提供重要的参考。
振动;Newmark-β;MATLAB;载荷识别
0 引言
随着对振动问题的研究深入,人们逐渐对振动反问题的研究产生了兴趣。反问题的研究可以追溯到20世纪的20年代,首先在雷达、医药领域内得到应用。对于正问题的求解是通过已知的载荷激励和系统的特性计算出动力响应,然而对于反问题的求解就要困难得多,因为反问题的求解需要涉及测量技术、数值算法以及工程判断等方面。在很多情况下,受限于各种条件的约束,很多设备并不允许在合理的测量点进行测量,往往只能在少数的点进行测量,进而得到位移响应或者是速度、加速度响应等,继而求解未知的压力或者作用力关于时间的历程。换热管束的振动问题作为换热器失效的主要形式之一,许多学者进行了大量的研究工作,在工艺和结构上都给出了一些有效的改善措施,例如限制壳程流速、改用折流杆型换热器等。但是,一方面由于流体流动本身的复杂性;另一方面,相关的实验由于受空间和环境的限制,并不能很好地模拟出真实的流场分布,振动问题并没有得到完美的解决。本文以换热设备的换热管为研究对象,采用Newmark-β法对其振动进行载荷识别分析,可以给换热管振动的防振设计作重要的参考。
1 基于Newmark-β法的载荷识别
采用时域内的动载荷识别技术来对单根换热管模型进行流体激励载荷的识别。换热器管束振动的动载荷识别问题,也即通过传感器测得的管束响应情况(位移、速度、加速度等)和已知的系统特性,在一定的计算方法下,求解换热管束振动的激励载荷。
1.1 Newmark-β法分析原理
这里首先使用有限元的理论将结构进行离散化,形成一个多自由度的系统,运用虚位移理论,得到如式(1)形式结构的动力学平衡方程:
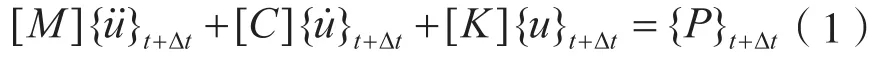
式中:[M] —— 结构的节点质量矩阵;
[C] —— 节点的阻尼矩阵;
[K] —— 结构的节点刚度矩阵;
其中,[M][C][K]三个量可以通过有限元理论构建获得。
当第t+Δt时刻之前的全部动力响应通过相应的传感器测量获得时,Newmark N M对位移、速度、加速度各响应间的关系作以下的假设:

可通过式(2)(3)中的两个参数α和β的调节,来对积分求解结果的精度和求解过程的稳定程度进行控制,学者大多认为当取α= 1/4,β= 1/2时为平均常加速度法,也可称为Euler-Guass法。
联立整理式(2)(3),可将第t时刻的位移,速度和加速度的值与第t+Δt时刻的速度和加速度值之间的关系以下面两个新的方式进行表述:
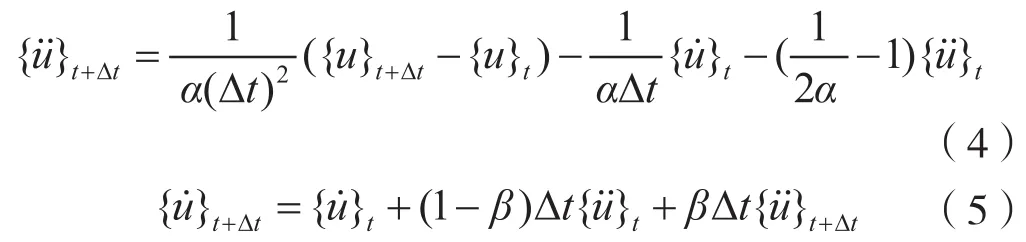
将式(4)和(5)代入式(1)得:
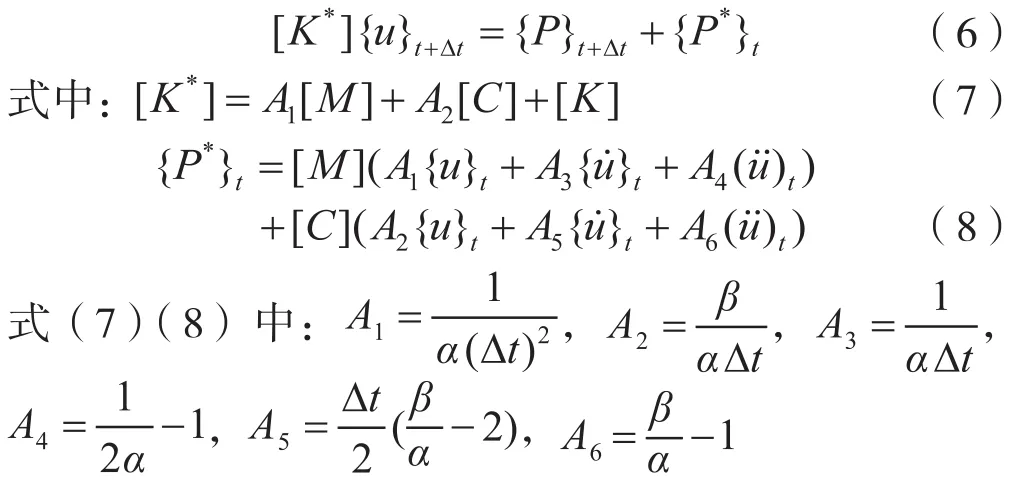
1.2 基于Newmark-β法的反分析原理
根据动载荷识别理论的第一类假定:线性假定,式(6)符合叠加原理,所以可以将之改写为以下的两个方程的联立形式:
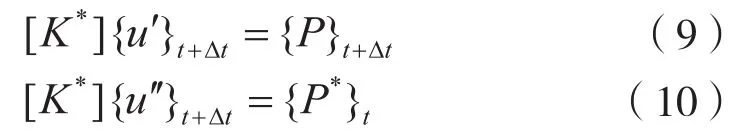
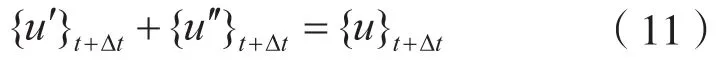
由于第t时刻的各动力响应参数为已知的值,则将第t时刻的响应值代入式(8)中,可以求出第t时刻的值,再将求得的代入式(10)中可求解出第t+Δt时刻的位移分量值:

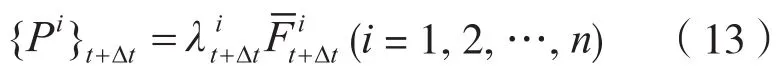
式中:n—— 施加载荷的节点数;
将式(13)代入式(9),可得:
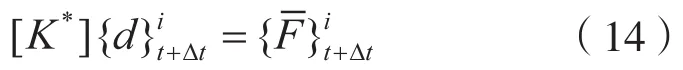
2.1.6 稳定性试验 取KC粉末0.30 g,精密称定,按照“2.1.3”项下方法制备试品溶液,室温放置,分别于0、4、8、12、16、20、24 h按照“2.1.1”项下色谱条件进样,记录峰面积,金丝桃苷、朝藿定B、朝藿定A、朝藿定C、淫羊藿苷、木犀草素、槲皮素、川陈皮素、山柰酚、宝藿苷I峰面积的RSD值分别为0.15%、0.58%、0.32%、1.11%、0.98%、1.58%、0.55%、0.68%、1.03%、0.25%,表明供试品溶液在室温下24 h内稳定。
对式(14)进行求解,可以分别得到在每个节点上施加单位载荷时所对应的结构的体系位移向量,再与式(13)相联,可以发现式(9)的解必然会满足以下的关系式:

当经过测量已经知晓了m个测点的振动响应,可以是位移值、速度值以及加速度值中的一种或者多种。
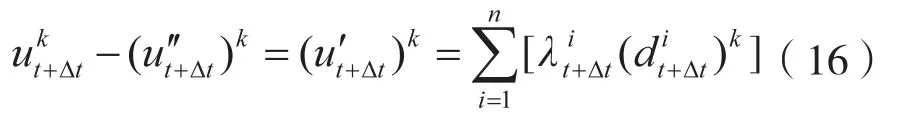
式 (16)实际上是由n个未知数 (i= 1, 2, …,n),m个方程组成的线性方程组,其中,n由待识别载荷节点的个数所决定,m则由测量点的个数所决定:
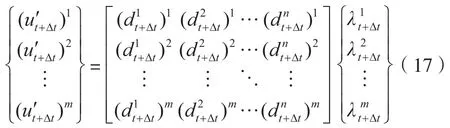
式(17)又可以改写成:

在求解式(17)的线性方程组时,如果想要这个线性方程组有解存在,则测量点的个数必须要等于或者是要大于待识别点的个数,即行数大于等于列数(m≥n),因为当测量点的个数小于待识别点的个数即行数小于列数(m<n)时,线性方程组无解,由式(17)求出之后,将其代入式(13)就可以算出第i个节点处的。
以上是在已知测点的位移响应时来计算结构载荷的方法,依照上面的方法,同理也可以通过速度或者加速度响应来计算结构载荷。
2 单根换热管的载荷识别
根据Newmark-β反分析原理,在Matlab中编写程序对单根换热管进行载荷识别的研究。
2.1 计算模型与参数
长为4 m的换热管,两端为固支约束,对换热管进行有限元划分,共分为29个单元,30个节点,60个自由度,通过对单元刚度矩阵k以及单元质量矩阵m的组装,形成模型的刚度矩阵K以及质量矩阵M,考虑管子的约束条件,在矩阵中进行删减,此处采用瑞利阻尼,阻尼矩阵C= 0.2M,具体的单元刚度矩阵以及单元质量矩阵如式(19)和式(20)所示:


换热管的具体参数见表1所示,
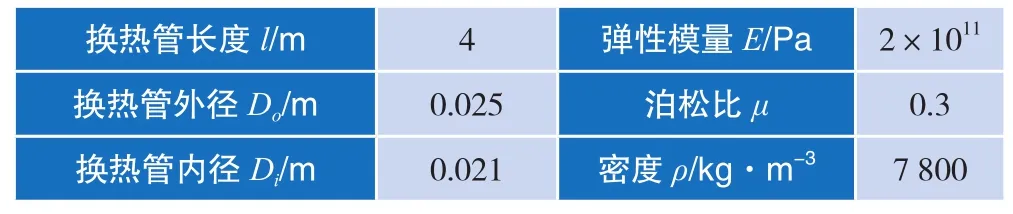
表1 换热管的具体参数
2.2 识别位置对识别结果的影响
在模型的第15,23节点上分别施加简谐激励为 -200 sin(4πt),100 sin(4πt),激励作用时间为 1 s,时间步长Δt= 0.01 s,具体模型如图1所示。
在Matlab软件中,选用Newmark-β法,以式(16)为基础,对该结构进行有限元编程。分别选取第7,9节点,第14,16节点,第21,22节点三组的速度响应作为测量响应。
分别选取每一个识别结果的四个峰值与原始力的峰值做差,来了解不同响应测量点识别结果离真实的载荷力之间的偏离程度,如表2所示。
对不同的测量点组求得的结果求误差水平估计值,见表3,对比图见图2。

图1 具体加载模型图

表2 不同测量点识别载荷与真实载荷峰值的差值

表3 不同测量点组的误差评估水平/%
从上面的各图表中,可以看出,在众多的测量点组当中,第15节点在以第14,16点为测量点时的识别结果较其他两组要好,而第23节点则以第21,22节点为测量点时的识别结果最好;另外可以发现的是,当选取靠近待识别点的点为测量点的识别结果要好于远离待识别点的测量点的识别结果。表明越接近载荷施加点位置处的响应越能够反应出施加载荷的信息,识别结果更加理想。

图2 不同测量点识别结果的误差水平估计对比图
3 结语
基于Newmark-β法,对换热管的振动进行了载荷识别研究,分析了在不同位置布置传感器测量结果对于识别结果的影响,表明越靠近载荷施加点的测量响应进行识别的结果越接近与真实的数值,这是因为其能更多地反应出未知载荷激励的信息。对后续换热管的防振设计有重要的参考作用。
[1] 张方,秦远田. 工程结构动载荷识别方法[M]. 北京:国防工业出版社,2011.
[2] 刘杰. 动态载荷识别的计算反求技术研究 [D]. 湖南大学,2011.
[3] 姜金辉,徐菁,张方,等. Wilson-θ 反分析法的动载荷识别精度的若干问题[J]. 振动. 测试与诊断,2013,33(5):782-788.
[4] De Araújo M,Antunes J,Piteau P. Remote identification of impact forces on loosely supported tubes:Part 1—Basic theory and experiments[J]. Journal of sound and vibration,1998,215(5):1015-1041.
[5] Antunes J,Paulino M,Piteau P. Remote identification of impact forces on loosely supported tubes:Part 2—Complex vibro-impact motions[J]. Journal of sound and vibration,1998,215(5):1043-1064.
[6] 陈英华. 动载荷时域 Wilson-θ 识别方法和 PATRAN 二次开发[D].南京航空航天大学,2010.
Application of load identification technique in vibration analysis
Chen Gong, Zeng Xianyu, Jin Lu, Yan Simin
(Shanghai Institute of Quality Inspection and Technical Research)
Taking tube heat transfer tube as the research object, the principle of positive and negative analysis of load identification based on Newmark- beta method is introduced. Through the preparation of the corresponding program in MATLAB, vibration of single tube heat exchanger for load identification is calculated, analyzed the influence of the placement of sensor for different load identification results, provides an important reference for anti vibration design and vibration for heat pipe.
vibration; Newmark-β; MATLAB; load identification

