结构方程模型在冬小麦农艺性状与产量关系分析中的应用

郑立飞尚一斐李学军冯 浩魏永胜

1西北农林科技大学生命科学学院, 陕西杨凌 712100;2西北农林科技大学理学院, 陕西杨凌 712100;3西北农林科技大学农学院, 陕西杨凌 712100;4西北农林科技大学国家节水灌溉杨凌技术研究中心, 陕西杨凌 712100

结构方程模型在冬小麦农艺性状与产量关系分析中的应用

郑立飞2尚一斐2李学军3冯 浩4魏永胜1,*

1西北农林科技大学生命科学学院, 陕西杨凌 712100;2西北农林科技大学理学院, 陕西杨凌 712100;3西北农林科技大学农学院, 陕西杨凌 712100;4西北农林科技大学国家节水灌溉杨凌技术研究中心, 陕西杨凌 712100

为探讨冬小麦主要农艺性状对产量的影响及各性状间的相互作用, 采用结构方程模型对2010—2011年度国家冬小麦品种试验中长江上游组(19个品种19个试点)的数据进行了分析, 调查性状包括产量(GY)、穗粒数(GNP)、基本苗(BS)、单位面积穗数(SN)、生育期(GD)、千粒重(TGW)和株高(PH)。其变异系数为 GY＞GNP＞SN＞BS＞PH＞TGW＞GD; 与产量的相关程度(相关系数绝对值)为 GNP＞BS＞SN＞GD＞TGW＞PH; 在多元回归分析中对产量的效应为 SN＞GNP＞TGW＞BS＞GD＞PH; 在结构方程模型中对产量的综合效应(直接效应与间接效应之和)为BS＞GNP＞TGW＞SN＞PH＞GD。结构方程模型既体现了主要农艺性状对产量的直接效应, 也体现了对产量的间接效应,并且作为先验模型, 可结合作物生理特性解释主要农艺性状对产量的影响。本研究结果表明, 应重视大穗多穗兼顾型冬小麦品种的选育。

冬小麦; 产量; 农艺性状; 结构方程模型

产量是小麦生产的主要目标之一, 不仅受到遗 传因素的影响, 也受到土壤肥力、气候条件以及农耕措施等因素的影响。产量构成三要素穗数、穗粒数和千粒重一直是高产育种栽培的研究重点, 其分析模型与方法也多种多样, 如多元线性回归[1-2]、通径分析[3-8]、主成分分析(principal component analysis, PCA)[9]、简单相关分析[2,5,8,10]和典型相关分析[11], 这些分析方法的根本目的是揭示冬小麦主要农艺性状与产量的关系, 为高产育种提供理论依据。

目前, 有关产量构成三要素对籽粒产量的贡献已有大量报道, 因为采用品种、样本量及试验条件不同, 其结论也不一致, 在特定条件下千粒重[3-4,7]、穗粒数[5]或单位面积穗数[6]都可能成为产量的主要贡献者。另外, 某些品种株高则是产量的主要决定因素[12]。为进一步明确冬小麦性状与产量的关系,我们利用结构方程模型(structural equation model, SEM, 有时covariance structure analysis, covariance structure modeling and analysis of covariance structures[13])作为一种多变量分析方法。最初该法主要用于社会科学领域, 后来应用于生态学中复杂问题的解析[14]。Lamb等[15]将SEM初步用于作物分析。相对于“第一代”多变量统计法PCA和聚类分析(cluster analysis, CA)等, SEM可称为“第二代”多变量统计法, 能够同时分析系统内多个变量间的因果关系,并明确给出各关系的强度大小[16]。本研究以19个冬小麦品种在19个不同地点的379套产量与主要农艺性状数据, 利用SEM分析主要农艺性状对产量的直接作用和间接作用, 以及各性状之间的关系, 为冬小麦高产品种的选育提供理论依据。

1 数据来源与分析方法

1.1 数据来源

数据来自2010—2011年度国家冬小麦品种试验中长江上游组区域试验, 共 19个品种或稳定品系,分别是15610、07-129、07间551-55、08RC2525、09J6白、09J76、BL228、BL379、CD09-2542、SW20812、川07217、川08品32(W)、川09023、川麦42 (2次对照)、川麦53、川重组104、绵06-374、太空7号和云麦59, 这些材料均为各育种单位选育的遗传性稳定的品系, 依据农业部颁发的《农作物品种(小麦)区域试验技术规程》新标准进行各试点的小区设计、田间管理及性状调查。选取19个栽培点的 379条数据。栽培点为甘肃省成县, 贵州省毕节县、贵阳市、铜仁市、遵义市、湖北省襄阳市、陕西省安康市、勉县, 重庆市北碚区、万州区、永川区, 四川省成都市、绵阳市、内江市、平昌县、西昌市及云南省楚雄州、德宏州、曲靖市。调查性状共 7个, 分别是生育期、基本苗、单位面积穗数、株高、千粒重、穗粒数及产量。

1.2 数据标准化

为了消除数据单位对分析的影响, 原始数据进行Z-score标准化处理。

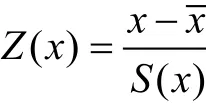
利用IBM SPSS AMOS 21 (Amos Development Corporation, Chicago, IL, USA)建立结构方程模型,并利用SPSS 16软件进行数据基本特征、正态性检验和相关性分析。

1.3 初始结构方程模型

结构方程模型是一种先验模型[14], 需要先在实践经验与理论的基础上建立假设路径, 再通过结构方程模型分析、验证和优化各因素间的直接和间接关系, 最终确定因素间合理的因果关系[15]。本研究的初始模型如图1所示。

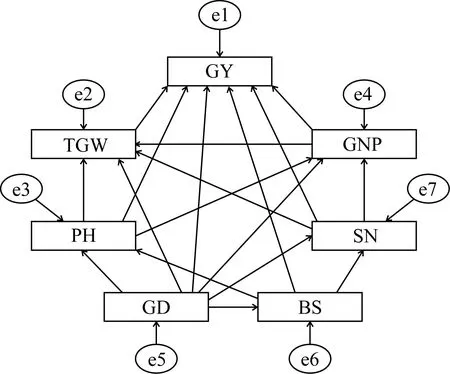
图1 冬小麦主要农艺性状与产量关系的初始模型Fig. 1 Initial modeling for the relationship between yield andagronomic traits in winter wheat

根据文献[6,12,15]及多年育种经验, 初始模型中假设千粒重、株高、穗粒数、生育期、基本苗、单位面积穗数对产量都有直接影响; 株高、生育期、单位面积穗数和穗粒数对千粒重有直接影响; 株高、生育期和单位面积穗数对穗粒数有直接影响;生育期和基本苗对株高和单位面积穗数有直接影响, 因为生育期包括冬前生长和次年生长, 因此假设生育期长可得到更多分蘖, 进而获得更多的穗数。设定初始模型后需要估计25个参数(图1), 少于可以建立的方程总数[7(7+1)/2=28], 因此该模型是可以识别的。

在结构方程模型分析之前, 作为比较, 采用向后逐步回归方法对数据进行多元回归分析, 根据 P值大小逐一剔除变量, P ＞ 0.05则剔除该变量。本研究的变量 P值均小于 0.05, 因此只进行一步回归分析。

1.4 模型检验

采用 χ2检验整体评价模型[17], χ2值越小, 模型的拟合效果越好。若 P＞0.05, 则表明模型没有遗漏重要参数。本研究中共有 379个数据点, 满足结构方程模型 χ2检验所需要的最小推荐样本数, 即模型参数的5倍以上[14]。用RMSEA (root mean square error of approximation)和 AIC (akaike information criterion)辅助检测模型的拟合度[18]。RMSEA ＜ 0.05,模型拟合非常好; 0.05 ≤ RMSEA ＜ 0.08, 模型拟合较好; 0.08 ≤RMSEA ＜ 0.10, 模型拟合一般; RMSEA ≥ 0.10, 模型拟合不好。AIC值越小, 模型的拟合度越高。

2 结果与分析

2.1 冬小麦数据的基本统计量

如表1所示, 最高产量为SW20812的9270.0 kg hm–2, 出现在云南德宏试点, 而在重庆永川点的云麦59产量最低, 为1861.5 kg hm–2, 极差达7408.5 kg hm–2, 变异系数是所有性状中最大的。千粒重变异范围为 27.3～62.2 g, 最低为种植于四川成都的15610, 最高为种植于四川西昌的 07间 551-55。株高分布范围为 47～118 cm, 最低为种植于甘肃成县的07-129, 最高为种植于重庆永川的云麦59。穗粒数最少的是种植于四川平昌的07间551-55, 为每穗20.6粒, 最多的是种植于云南德宏州的 07-129, 为每穗72.9粒。生育期变幅为142～232 d, 是测定性状中变异最小的, 除遗传特性外, 与试点纬度等关系密切, 其中在甘肃成县生育期最长(230.0±0.8 d), 在云南德宏生育期最短(154.0±5.4 d)。基本苗最低的是种植于甘肃省成县的15610, 为每公顷102万株, 最高的是种植于四川省西昌市的川重组 104, 为每公顷 292.5万株。单位面积穗数最低的为种植于贵州省铜仁市的BL228, 为每公顷240万穗, 最高的为种植于湖北省襄阳市的川07217, 为每公顷630万穗。

2.2 冬小麦主要农艺性状与产量的相关性分析

除株高外的其余性状与产量的相关性均达到显著水平, 其中穗粒数、基本苗和单位面积穗数与产量的相关系数较高, 生育期与产量呈显著负相关;除产量外的各农艺性状之间也存在显著相关(表2)。因此, 有必要对各农艺性状与产量的直接和间接关系作进一步分析。

2.3 冬小麦主要农艺性状与产量的回归分析

冬小麦产量(Ŷ)与千粒重(x1)、株高(x2)、穗粒数(x3)、生育期(x4)、基本苗(x5)、单位面积穗数(x6)的多元回归方程为 Ŷ = 109.5x1+ 15.1x2+ 99.8x3+ 12.8x4+ 12.7x5+ 11.4x6-13720.1 (R2= 0.719), 自变量的标准化系数分别为0.440、0.125、0.557、0.156、0.301和 0.601。因此, 各性状对冬小麦产量的影响,由大到小依次为单位面积穗数、穗粒数、千粒重、基本苗、生育期和株高。

2.4 冬小麦主要农艺性状与产量的结构方程模型分析

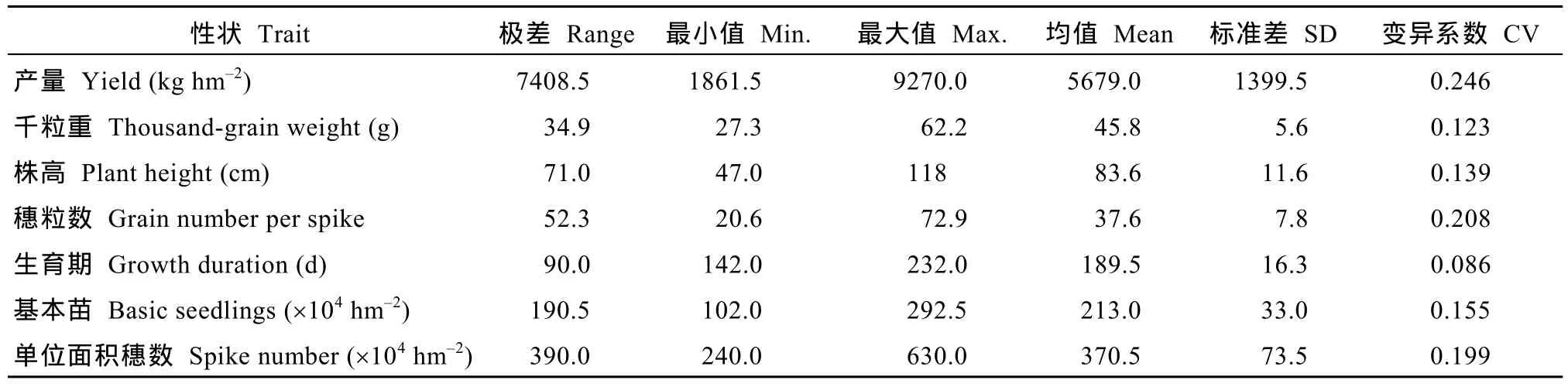
表1 本研究中冬小麦各性状的基本统计量Table 1 Basic statistics of winter wheat traits used in this study (n = 379)

初始模型拟合结果, χ2为 36.665, 自由度(df)为4, χ2/df为9.164, P＜0.05, 而RMR和RMSEA均大于0.05 (表3), 因此模型需要修订。修订时保留通径系数显著的, 删除不显著的。结构方程模型作为一种先验模型, 允许根据作物的生长实际, 保留一些统计上不显著但有一定生物学意义的路径。最终在初始模型的基础上, 我们增加了单位面积穗数到株高的路径, 去除了单位面积穗数到穗粒数的路径。修订模型参数见表3, P值为0.199, RMR和RMSEA均小于0.05。

表2 冬小麦性状的相关系数Table 2 Correlation coefficients among winter wheat traits

表3 初始与最终结构方程模型的主要拟合指标Table 3 Initial and final fit indices of structural equation model

图2 结构方程模型中冬小麦主要性状对产量的影响及各性状间的关系Fig. 2 Effects of agronomic traits on yield of winter wheat and relationships among agronomic traits as results of structural equation modeling

在最终建立的结构方程模型中, 各农艺性状对产量的直接效应均为正效应, 其中单位面积穗数、穗粒数、千粒重对产量的影响较大, 通径系数分别为 0.60、0.56和 0.44; 基本苗对产量的通径系数为0.30; 而株高和生育期则对产量的影响较小。除了直接效应以外, 各性状还通过彼此的间接效应对最终产量发挥作用(图2)。如单位面积穗数和穗粒数对千粒重的影响均为负向, 标准化通径系数分别为-0.45和-0.18; 生育期则对株高和基本苗有负效应, 标准化通径系数分别为-0.56和-0.50; 单位面积穗数对穗粒数的影响则很小。因此, 各性状对产量的影响应按结构方程模型所示, 需要综合直接效应与间接效应进行评价, 讨论总效应。单位面积穗数对产量的直接效应为 0.60, 通过千粒重、穗粒数和株高的间接效应分别为-0.20、-0.02和 0.01, 总效应为0.39(表4)。千粒重对产量的最终效应系数是0.44。穗粒数对产量的直接效应为 0.56, 但穗粒数与千粒重呈负相关, 即穗粒数越多, 籽粒越小, 这与生产实践中的结果是一致的。由于穗分化在先、灌浆在后, 因此穗粒数通过千粒重对产量产生间接影响(-0.08), 穗粒数对产量最终的效应为 0.48。株高对产量的直接效应系数为0.13 (图2), 但株高分别通过千粒重(-0.03)和穗粒数(-0.06)对产量有负的影响,因此, 其对产量的最终效应系数仅为 0.04。基本苗的直接效应系数为 0.30, 通过单位面积穗数、千粒重和株高效应系数分别为0.12、0.08和-0.01, 最终的效应系数为 0.49。生育期对产量的直接效应为0.16, 通过株高、穗粒数、单位面积穗数和基本苗的效应系数分别为-0.02、-0.15、0.11和-0.25, 最终作用为-0.15。从决定系数看, 各性状随机误差的决定系数均高(0.74～0.99), 而产量的决定系数达到 0.72,与回归分析结果一致, 产量随机误差决定系数为0.28 (图2)。这表明生产中冬小麦所处环境的随机变化对各农艺性状的影响较大, 而这些性状特征一旦确定, 最终的产量也就基本确定了。

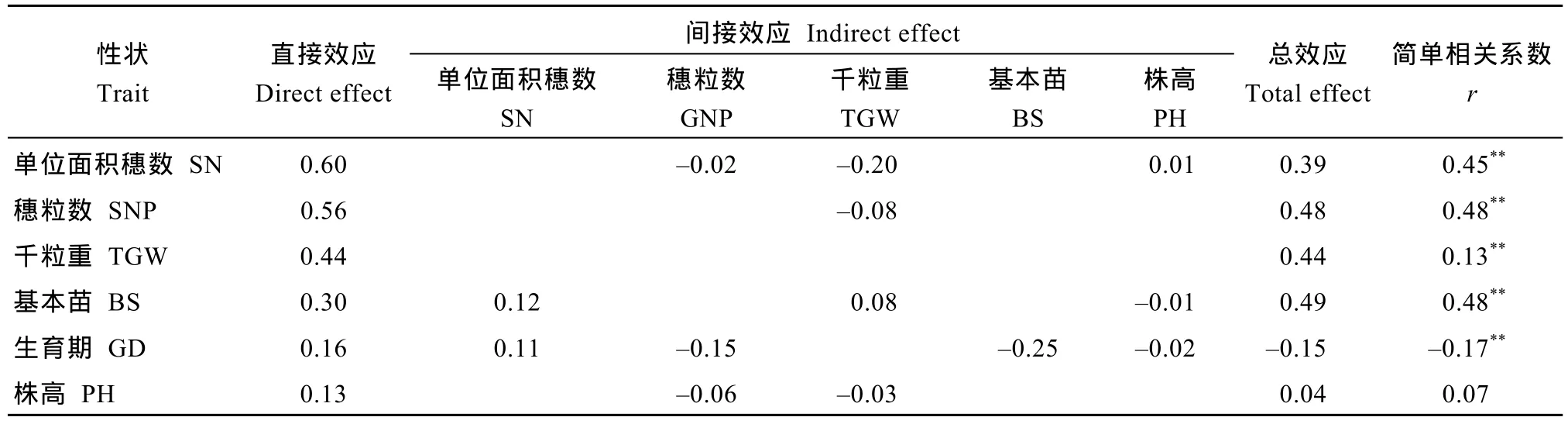
表4 冬小麦主要农艺性状对产量的直接及间接效应Table 4 Direct and indirect effects of agronomic traits on yield of winter wheat

3 讨论

本研究所涉及的冬小麦产量基本数据(表 1)变异系数最大的为产量(0.246), 其次为穗粒数(0.208)和单位面积穗数(0.199), 最小的是生育期(0.086),表明产量因品种和栽培地不同存在较大差异, 这种差异更多的可能是由穗粒数和单位面积穗数的变异造成的, 而生育期相对变化小, 对产量的影响可能也较小。这与相关性分析结果(表2)所得判断有相似之处, 即穗粒数和单位面积穗数影响较大, 相关系数分别0.48和0.45, 但相关分析结果显示基本苗也对产量影响较大, 相关系数为 0.48, 而株高对产量影响最小。

通过结构方程模型分析的结果表明, 各性状对产量总的效应与相关分析和回归分析的结果是不同的。结构方程模型中各性状的直接通径系数与多元回归方程中的标准化系数相同, 评估后的总效应系数则发生了变化, 其中单位面积穗数、穗粒数、株高和生育期的效应下降, 尤其是生育期, 其效应由正转负, 系数由0.16转变-0.16。而基本苗的总效应则由原来0.30增加到0.50。总的效应系数与性状产量相关系数判断的正负方向是一致的, 但具体数值不同(表 4)。效应排序为基本苗＞穗粒数＞千粒重＞单位面积穗数＞株高＞生育期。

基本苗对产量的直接效应低于单位面积穗数、穗粒数和千粒重, 但加上通过单位面积穗数和千粒重对产量的间接效应后, 总的效应上升为第 1位。因此推论, 本研究中所涉及的地区、品种在栽培时播种量有进一步提高空间。穗粒数和千粒重同为穗部特征, 在假设光合产物供应一定的情况, 穗粒数的增加可能会导致千粒重下降(表2)。从发育过程看,穗粒数的分化在先, 籽粒灌浆在后, 所以在结构方程模型分析过程中允许考虑穗粒数对千粒重的影响,不需要考虑千粒重对穗粒数的影响, 这也是先验模型的优势所在。理论上千粒重主要决定于灌浆程度,而本研究中缺少评价灌浆的相关指标, 因此其直接效应即为最终效应。单位面积穗数的效应因通过千粒重对产量的间接负效应而削弱, 最终低于千粒重的直接效应。单位面积穗数分别通过千粒重和穗粒数对产量的间接作用均为负值, 尤其是通过千粒重的负向影响较大, 与千粒重对产量的直接效应相同。生育期对产量的直接效应是正向的, 从生理中可解释为长的生育期有利于延长总光合时间, 进而增加光合产物, 但生育期通过穗粒数和基本苗对产量有负效应, 最终导致生育期对产量也是负向影响。无论是哪一种分析方法, 株高对产量的影响都是最小的, 表明这些育成品种株高可能已经接近最适状态。

4 结论

通过结构方程模型分析, 长江上游冬小麦区域试验 19个冬小麦品种在栽培中播种量有进一步提高空间, 穗部特征对产量的影响高于单位面积穗数、株高和生育期, 在选育工作中应重点关注穗部性状。结构方程模型作为一种先验模型可应用于作物研究, 分析多变量关系, 尤其是多响应变量, 探讨其内部作用过程与机制。

[1] Chamekha Z, Karmousb C, Ayadia S, Sahlia A, Hammamia Z, Frajc M B, Benaissaa N, Trifaa Y, Slim-Amaraaa H. Stability analysis of yield component traits in 25 durum wheat (Triticum durum Desf.) genotypes under contrasting irrigation water salinity. Agric Water Manag, 2015, 152: 1–6

[2] Bhutto A H, Rajpar A A, Kalhoro S A, Ali A, Kalhoro F A, Ahmed M, Raza S, Kalhoro N A. Correlation and regression analysis for yield traits in wheat (Triticum aestivum L.) genotypes. Nat Sci, 2016, 8: 96–104

[3] de Oliveira Gondim T C, Rocha V S, Sediyama C S, Miranda G V. Path analysis for yield components and agronomic traits of wheat under defoliation. Pesquisa Agropecuaria Brasileira, 2008, 43: 487–493

[4] Siney S M A, Saba J. Analysis of yield and yield components traits in twenty bread wheat genotypes under dry land conditions. Philippine J Crop Sci, 2015, 40: 78–84

[5] Okuyama L A, Federizzi L C, Neto J F B. Correlation and path analysis of yield and its components and plant traits in wheat. Ciencia Rural, 2004. 34: 1701–1708

[6] 田纪春, 邓志英, 胡瑞波, 王延训. 不同类型超级小麦产量构成因素及籽粒产量的通径分析. 作物学报, 2006, 32: 1699–1705

Tian J C, Deng Z Y, Hu R B, Wang Y X. Yield Components of super wheat cultivars with different types and the path coefficient analysis on grain yield. Acta Agron Sin, 2006, 32: 1699–1705 (in Chinese with English abstract)

[7] Yagdi K. Path coefficient analysis of some yield components in durum wheat (Triticum durum Desf.). Pakistan J Bot, 2009, 41: 745–751

[8] Çifci E A. Estimate of heterosis, correlation and path analysis for grain yield per spike and some agronomic traits on durum wheat (Triticum durum Desf.). J Anim Plant Sci, 2012, 22: 747–752

[9] Janmohammadi M, Movahedi Z, Sabaghnia N. Multivariate statistical analysis of some traits of bread wheat for breeding under rainfed conditions. J Agric Sci, Belgrade, 2014, 59: 1–14

[10] Behmanesh S, Taghizadeh R, Zaefizadeh M. Analysis of yield and yield components in durum wheat. Int Res J Appl Basic Sci, 2013, 4: 3333–3337

[11] Carvalho I R, De Souza V Q, Nardino M, Follmann D N, Schmidt D, Baretta D. Canonical correlations between morphological traits and yield components in dual-purpose wheat. Pesquisa Agropecuaria Brasileira, 2015, 50: 690–697

[12] 金艳, 宋佳静, 朱统泉, 陈杰, 赵立尚. 2001–2015年河南省审定小麦品种产量构成分析. 中国种业, 2016, (4): 41–44

Jin Y, Song J J, Zhu T Q, Chen J, Zhao L S. Analysis for yield components of wheat varieties registered and released in Henan province in 2001–2015. China Seed Ind, 2016, (4): 41–44 (in Chinese)

[13] Kline R B. Principles and Practice of Structural Equation Modeling. 3rd Edn. New York, NY: Guilford Press, 2011

[14] Grace J B. Structural Equation Modeling and Natural Systems. Cambridge, UK: Cambridge University Press, 2006

[15] Lamb E G, Shirtliffe S J, May W E, Structural equation modeling in the plant sciences: an example using yield components in oat. Can J Plant Sci, 2011, 91: 603–619

[16] Fornell C. A second Generation of Multivariate Analysis V1. New York, NY: Praeger Publishes, 1982

[17] Schermelleh-Engel K, Moosbrugger H, Müller H. Evaluating the fit of structural equation models: test of significance and descriptive goodness of fit measures. Methods Psychol Res Online, 2003, 8: 23–74

[18] 王卫东. 结构方程模型原理与应用. 北京: 中国人民大学出版社, 2010

Wang W D. Theory and Application of Structural Equation Modeling, Beijing: China Renmin University Press, 2010 (in Chinese)

Structural Equation Model for Analyzing Relationship between Yield and Agronomic Traits in Winter Wheat

ZHENG Li-Fei2, SHANG Yi-Fei2, LI Xue-Jun3, FENG Hao4, and WEI Yong-Sheng1,*

1College of Life Sciences, Northwest A&F University, Yangling 712100, China;2College of Science, Northwest A&F University, Yangling 712100, China;3College of Agronomy, Northwest A&F University, Yangling 712100, China;4China Water Saving Irrigation Institute, Northwest A&F University, Yangling 712100, China

This study aimed at understanding the relationship between winter wheat yield and major agronomic traits using structural equation model. The parameters collected from the 2010–2011 National Winter Wheat Region Trail for Upper Yangtze River Group (19 varieties in 19 locations) were grain yield (GY), grain number per spike (GNP), density of basic seedlings (BS), spike number per ha (SN), growth duration (GD), thousand-grain weight (TGW), and plant height (PH). The variance coefficient in structural equation model showed a trend of GY ＞ GNP ＞ SN ＞ BS ＞ PH ＞ TGW ＞ GD. According to Pearson correlation, the correlation levels with yield was GNP ＞ BS ＞ SN ＞ GD ＞ TGW ＞ PH. The effect of a single trait on yield was SN ＞ GNP ＞TGW ＞ BS ＞ GD ＞ PH according to multiple regression analysis and BS ＞ GNP ＞ TGW ＞ SN ＞ PH ＞ GD according to the sum of direct and indirect effects in structural equation model. Both direct and indirect effects of agronomic traits in winter wheat on yield can be explained by structural equation model. As a prior experimental model, structural equation model can be used to analysis the complex relationship between crop physiological properties and wheat yield. Our results suggest that large- and multi-spikes need to be considered simultaneously in winter wheat breeding.

Winter wheat; Yield; Agronomic traits; Structural equation model

(

): 2016-12-07; Accepted(接受日期): 2017-05-10; Published online(网络出版日期): 2017-06-05.

10.3724/SP.J.1006.2017.01395

本研究由国家高技术研究发展计划(863计划)项目(2013AA102904), 西北农林科技大学基本科研业务费专项资金(2014YB023)和西北农林科技大学本科优质课程建设项目资助。

This study was supported by the National High Technology Research and Development Program of China (2013AA102904), the Special Funds for Research Activities in Northwest A&F University (2014YB023), and the Quality Curriculum project in Northwest A&F University.

*通讯作者(Corresponding author): 魏永胜, E-mail: wysh70@nwsuaf.edu.cn

联系方式: E-mail: zhenglifei@nwsuaf.edu.cn

URL: http://kns.cnki.net/kcms/detail/11.1809.S.20170605.1650.010.html